
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тема 2. СЛОЖНЫЕ ПРОЦЕНТЫ
|
Читайте также: |
При использовании сложных процентов база для начисления процентов увеличивается от периода к периоду, т.е. процесс наращения капитала происходит с ускорением. Механизм возрастания капитала по сложным процентам называют капитализацией. Различают годовую капитализацию, полугодовую, квартальную, месячную и ежедневную.
Наращенная сумма сложных декурсивных процентов определяется по формуле:
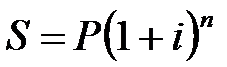 , (2.1)
, (2.1)
где P – первоначальная величина капитала (кредита, депозита, ссуды и т.д.),
S – наращенная сумма капитала на конец срока финансовой операции,
n – срок финансовой операции, лет,
i – годовая ставка процентов, выраженная десятичной дробью.
Сумма начисленных процентов I составляет:
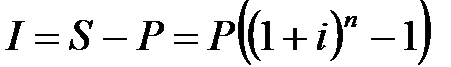 . (2.2)
. (2.2)
Если используются переменные значения процентной ставки во времени, то наращенная сумма определяется по формуле:
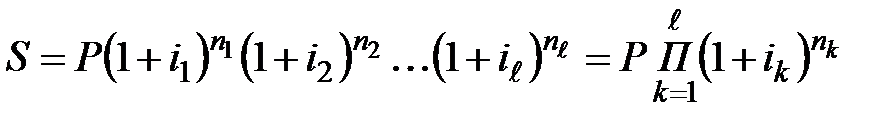 , (2.3)
, (2.3)
где  – последовательные значения переменной процентной ставки,
– последовательные значения переменной процентной ставки,
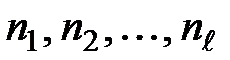 – продолжительность периодов (лет), к которым приурочены соответствующие значения процентной ставки,
– продолжительность периодов (лет), к которым приурочены соответствующие значения процентной ставки,
ℓ – число значений процентной ставки.
Часто срок финансовой операции является не целым, а дробным числом. Для определения наращенной суммы капитала в этом случае используют два метода:
а) общий 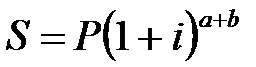 , (2.4)
, (2.4)
б) смешанный 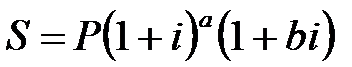 , (2.5)
, (2.5)
где 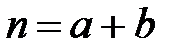 – срок финансовой операции, лет;
– срок финансовой операции, лет; 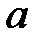 – целое число лет,
– целое число лет, 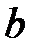 – дробная часть года.
– дробная часть года.
Аналогичный метод применяется и в случаях, когда периодом начисления является полугодие, квартал или месяц, а также при использовании учетной ставки d.
Множитель наращения по смешанному методу оказывается несколько больше, чем по общему.
Проценты капитализируются не только один, а несколько раз в году – по полугодиям, кварталам, месяцам (даже ежедневно). В контрактах при этом указывается не ставка за период начисления ( 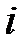 ), а годовая ставка (
), а годовая ставка ( 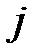 ), одновременно указывается период начисления процентов. Годовая процентная ставка j называется номинальной.
), одновременно указывается период начисления процентов. Годовая процентная ставка j называется номинальной.
Формула наращения процентов при этом имеет вид:
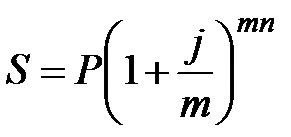 , (2.6)
, (2.6)
где 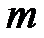 – число начисления процентов в году (ежегодное начисление m = 1; по полугодиям, m = 2; ежеквартальное, m = 4; ежемесячное, m = 12; ежедневное, m=365).
– число начисления процентов в году (ежегодное начисление m = 1; по полугодиям, m = 2; ежеквартальное, m = 4; ежемесячное, m = 12; ежедневное, m=365).
Наращение по сложной учетной ставке осуществляется по формулам:
а) при ежегодном начислении процентов (m=1)
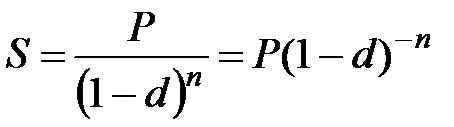 ; (2.7)
; (2.7)
б) при m-разовом начислении процентов (m>1)
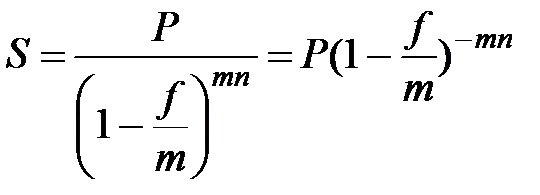 . (2.8)
. (2.8)
Если используются переменные значения учетной ставки, то наращенная сумма определяется по формуле:
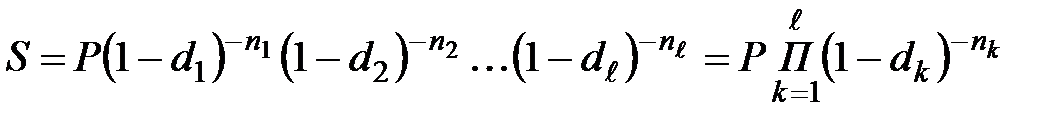 . (2.9)
. (2.9)
Дисконтирование по сложной ставке процента может быть математическим и банковским.
Математическое дисконтирование заключается в определении современной величины капитала P по значению наращенной суммы S с использованием сложной ставки декурсивных процентов. Современная стоимость капитала составит:
а) при ежегодном начислении процентов
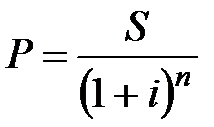 ; (2.10)
; (2.10)
б) при m-разовом начислении процентов в году
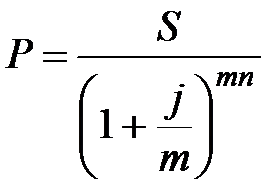 . (2.11)
. (2.11)
Банковское дисконтирование по сложной учетной ставке может быть использовано при учете среднесрочных и долгосрочных долговых обязательств. Дисконтированная величина долгового обязательства составит:
а) при ежегодном начислении процентов
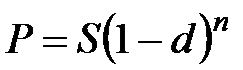 ; (2.12)
; (2.12)
б) при m-разовом начислении процентов
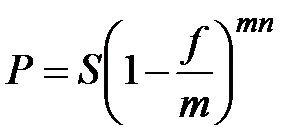 . (2.13)
. (2.13)
Таблица 2.1 - Определение срока финансовой операции и ставки процента
| Декурсивные проценты | Антисипативные проценты | ||
| m=1 | m>1 | m=1 | m>1 |
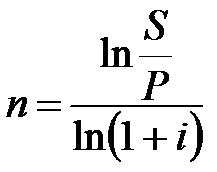 (2.14) (2.14)
| 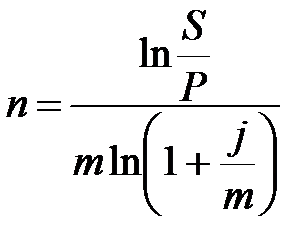 (2.16) (2.16)
|  (2.18) (2.18)
| 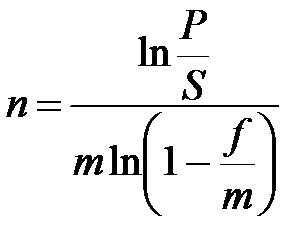 (2.20) (2.20)
|
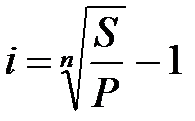 (2.15) (2.15)
| 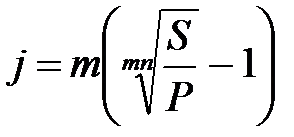 (2.17) (2.17)
| 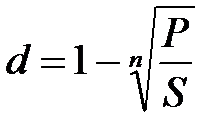 (2.19) (2.19)
| 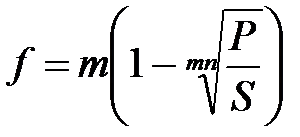 (2.21) (2.21)
|
При непрерывном наращении процентов применяют силу роста, которая характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.
Постоянная сила роста ( 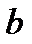 ) представляет собой номинальную ставку сложных процентов при
) представляет собой номинальную ставку сложных процентов при 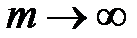 . Наращенная сумма капитала составит
. Наращенная сумма капитала составит
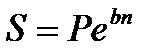 , (2.22)
, (2.22)
а современная стоимость 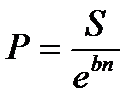 . (2.23)
. (2.23)
Переменная сила роста ( 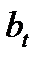 ) изменяется во времени, следуя закону, представленному в виде непрерывной функции времени
) изменяется во времени, следуя закону, представленному в виде непрерывной функции времени 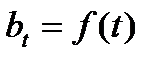 .
.
Линейная функция:
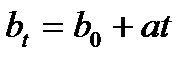 , (2.24)
, (2.24)
где 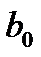 – начальное значение силы роста, а – прирост силы роста в единицу времени.
– начальное значение силы роста, а – прирост силы роста в единицу времени.
Наращенная сумма капитала составит:
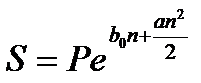 , (2.25)
, (2.25)
а современная стоимость:
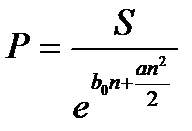 . (2.26)
. (2.26)
Экспоненциальная функция:
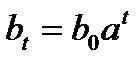 , (2.27)
, (2.27)
где 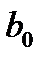 – начальное значение силы роста, а – постоянный коэффициент роста.
– начальное значение силы роста, а – постоянный коэффициент роста.
Наращенная сумма капитала составит:
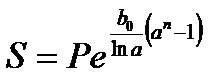 , (2.28)
, (2.28)
а современная стоимость:
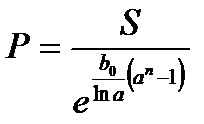 . (2.29)
. (2.29)
Таблица 2.2 - Определение срока финансовой операции и силы роста
| Постоянная сила роста | Переменная сила роста (экспоненциальная) |
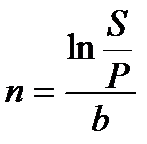 (2.30) (2.30)
| 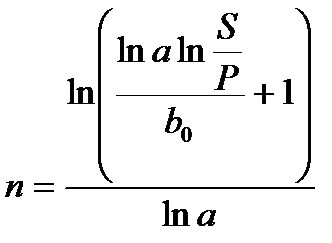 (2.32) (2.32)
|
 (2.31) (2.31)
| 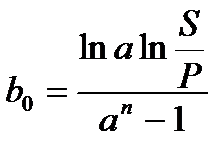 (2.33) (2.33)
|
Налогообложение процентного дохода уменьшает реальную наращенную сумму и доходность депозитной операции. Если начисляются простые проценты, то сумма налога на проценты L за весь срок финансовой операции составит:
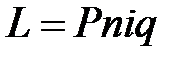 , (2.34)
, (2.34)
где q – ставка налога на проценты.
Наращенная сумма с учетом выплаты налога:
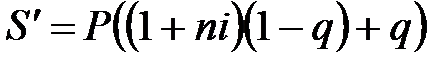 . (2.35)
. (2.35)
При долгосрочных операциях и начислении сложных процентов сумма налога на проценты определяется по формуле:
 . (2.36)
. (2.36)
Наращенная сумма с учетом выплаты налога:
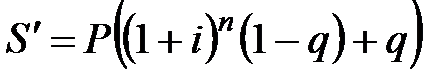 . (2.37)
. (2.37)
Сумма налога на проценты 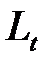 за каждый год отдельно составляет:
за каждый год отдельно составляет:
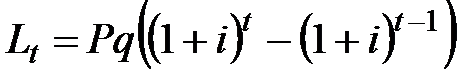 , (2.38)
, (2.38)
где t – порядковый номер года.
Наращенная сумма с учетом влияния инфляции (C) по схеме простых процентов определяется по формулам:
а) декурсивные проценты
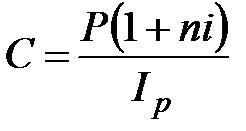 ; (2.39)
; (2.39)
б) антисипативные проценты
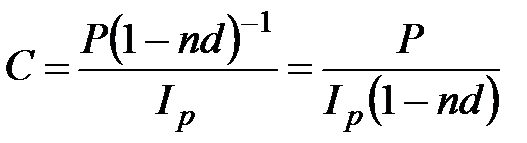 , (2.40)
, (2.40)
где 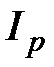 – индекс цен за соответствующий период n (эту величину также называют индексом инфляции за период n).
– индекс цен за соответствующий период n (эту величину также называют индексом инфляции за период n).
Соответственно, темп прироста инфляции hn за период времени n лет составит: 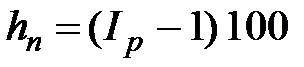 . (2.41)
. (2.41)
Индекс инфляции 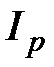 за весь период в n лет при известных темпах прироста инфляции за составляющие его подпериоды:
за весь период в n лет при известных темпах прироста инфляции за составляющие его подпериоды:
 , (2.42)
, (2.42)
где 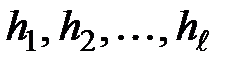 – темпы прироста инфляции за соответствующие подпериоды, %;
– темпы прироста инфляции за соответствующие подпериоды, %;
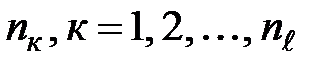 – период действия соответствующего темпа прироста
– период действия соответствующего темпа прироста
инфляции, 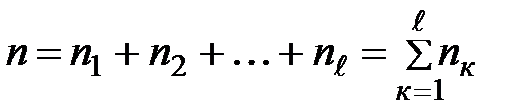 .
.
Наращенная сумма с учетом влияния инфляции по схеме сложных процентов определяется по формулам:
а) декурсивные проценты
 , при m=1;
, при m=1; 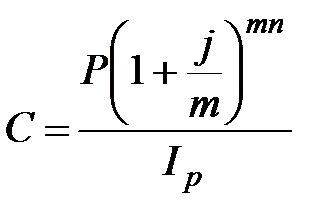 , при m>1; (2.43)
, при m>1; (2.43)
б) антисипативные проценты
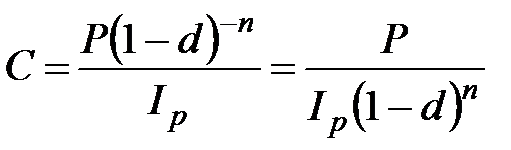 , при m=1; (2.44)
, при m=1; (2.44)
 , при m>1; (2.45)
, при m>1; (2.45)
в) непрерывные проценты
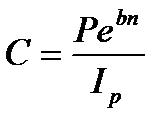 . (2.46)
. (2.46)
Реальная доходность финансовой операции с учетом инфляции измеряется с помощью соответствующих ставок процента:
а) по схеме простых процентов
 ;
;  ; (2.47)
; (2.47)
б) по схеме сложных процентов
 ,
, 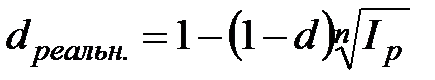 , при m=1; (2.48)
, при m=1; (2.48)
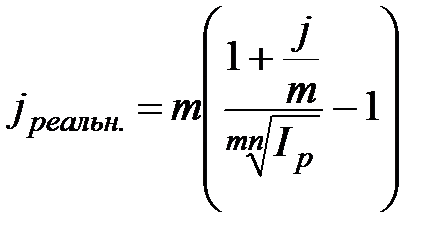 ,
, 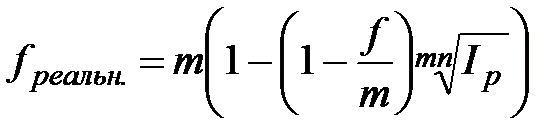 , при m>1; (2.49)
, при m>1; (2.49)
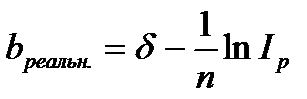 ,
, 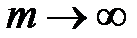 . (2.50)
. (2.50)
Минимальная ставка процента, нейтрализующая действие инфляции, определяется из равенства индекса инфляции и соответствующего множителя наращения. Если начисляются сложные декурсивные проценты по ставке i за n лет, а индекс инфляции за этот же период составил 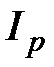 , то:
, то:
 , откуда
, откуда 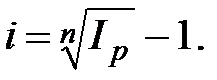 (2.51)
(2.51)
Для обеспечения реального наращения капитала в условиях инфляции должно выполняться неравенство 
В целях компенсации потерь от снижения покупательной способности денег ставку процента корректируют с учетом темпа инфляции. Величина корректирующей брутто-ставки r, которая обеспечивает реальную доходность финансовой операции по заданной ставке процента, определяется по формулам:
а) по схеме простых процентов
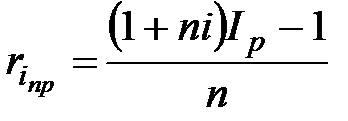 ;
; 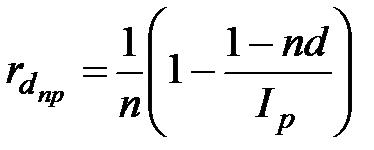 ; (2.52)
; (2.52)
б) по схеме сложных процентов
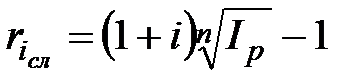 ,
, 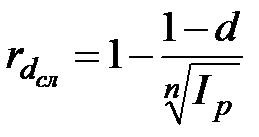 , при m=1; (2.53)
, при m=1; (2.53)
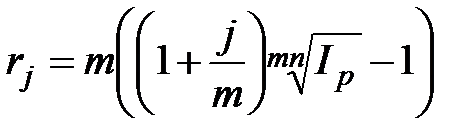 ,
, 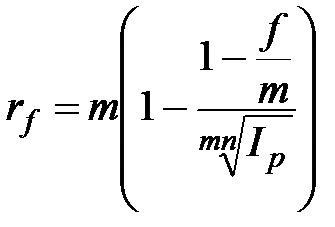 , при m>1; (2.54)
, при m>1; (2.54)
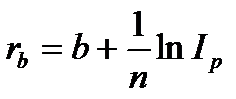 ,
,  . (2.55)
. (2.55)
Пример 2.1 Сумма 200 тыс. руб. инвестируется под процентную ставку 15 % годовых: 1) на 3 месяца; 2) на 6 месяцев; 3) на 1 год; 4) на 6 лет; 5) на 9 лет. Найти наращенные суммы по схеме простых и сложных процентов.
Решение.
1. По условию задачи n1=0,25 года, n2=0,5 года, n3=1 год, n4=6 лет, n5=9 лет, P=200000 руб., i=0,15. При наращении простых процентов по формуле (1.2) получим:
1.1. 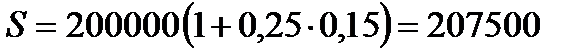 руб.
руб.
1.2. 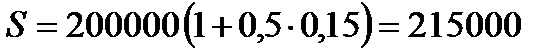 руб.
руб.
1.3. 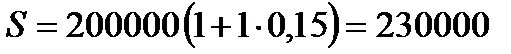 руб.
руб.
1.4. 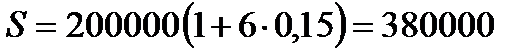 руб.
руб.
1.5. 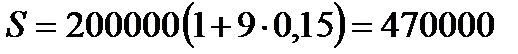 руб.
руб.
2. При наращении сложных процентов по формуле (2.1) получим:
2.1. 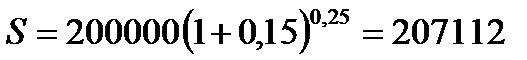 руб.
руб.
2.2. 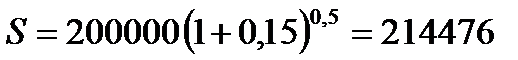 руб.
руб.
2.3. 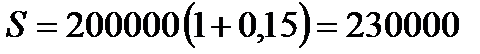 руб.
руб.
2.4. 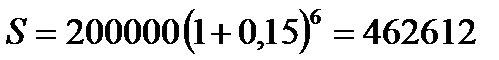 руб.
руб.
2.5. 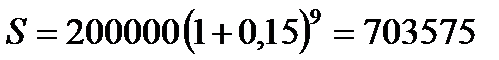 руб.
руб.
Для владельца капитала более выгодной является схема простых декурсивных процентов, если срок финансовой операции менее одного года; схема сложных декурсивных процентов – если срок превышает один год. При однократном начислении процентов и продолжительности периода один год обе схемы дают равные результаты.
Пример 2.2 В банке получена ссуда в размере 400 тыс. руб. на 8 лет на следующих условиях: для первых трех лет процентная ставка равна 10% годовых, на следующий год устанавливается маржа в размере 1%, а на последующие годы маржа равна 1,5%. Найдите сумму, которая должна быть возвращена банку по окончании срока ссуды при ежегодных начислениях сложных процентов.
Решение. Поскольку имеем дело с переменной процентной ставкой, то P=400000 руб., n1=3, n2=1, n3=4, i1=0,10, i2=0,11, i3=0,115. Используя формулу 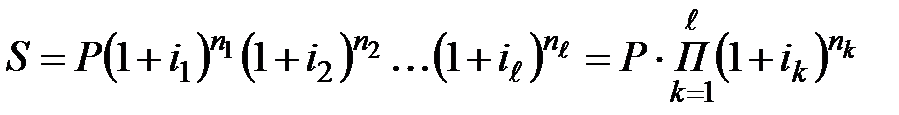 , получим:
, получим:
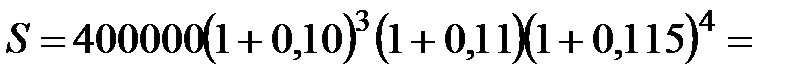 913398,92 руб.
913398,92 руб.
Пример 2.3 Предприниматель получил в банке ссуду в размере 50 тыс. руб. на 39 месяцев под процентную ставку 17% годовых на условиях начисления процентов: а) ежегодного; б) полугодичного. Какую сумму предприниматель должен будет вернуть банку по истечении срока при использовании схемы: сложных процентов, смешанной ?
Решение.
1. Так как срок финансовой операции выражается в месяцах, а проценты в первом варианте начисляются ежегодно, т.е. каждые 12 месяцев, то, разделив 39 месяцев на 12 месяцев, получим общее количество периодов начисления процентов или срок ссуды в годах:
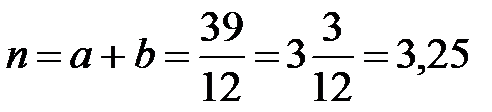 года, где a = 3, b=0,25. Остальные параметры ссуды составят: P = 50000 руб., i = 0,17. Наращенная сумма будет равна:
года, где a = 3, b=0,25. Остальные параметры ссуды составят: P = 50000 руб., i = 0,17. Наращенная сумма будет равна:
по схеме сложных процентов
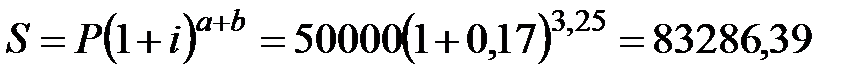 руб.;
руб.;
по смешанной схеме
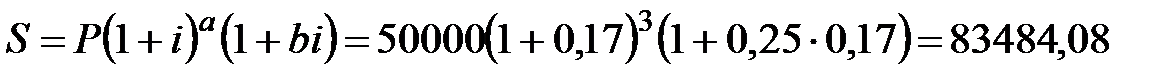 руб.
руб.
2. Так как срок финансовой операции выражается в месяцах, а проценты во втором варианте начисляются по полугодиям, т.е. каждые 6 месяцев, то, разделив 39 месяцев на 6 месяцев, получим общее количество периодов начисления процентов или срок ссуды в полугодиях:
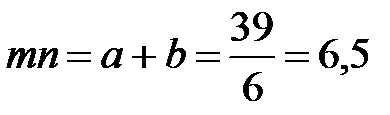 полугодий, где a=6 (a – целое количество периодов начисления процентов), b=0,5 (b – дробная часть одного периода). Наращенная сумма составит:
полугодий, где a=6 (a – целое количество периодов начисления процентов), b=0,5 (b – дробная часть одного периода). Наращенная сумма составит:
по схеме сложных процентов
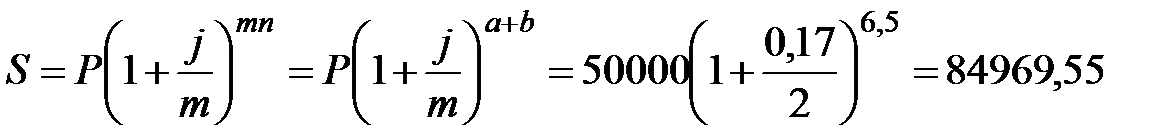 руб.;
руб.;
по смешанной схеме
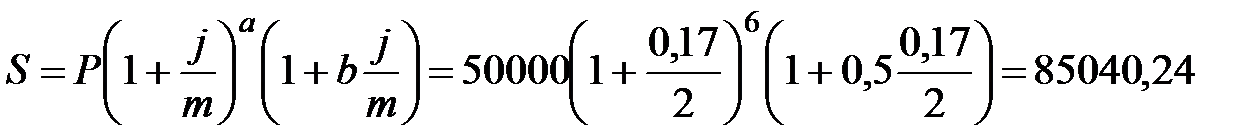 руб.
руб.
По смешанной схеме итоговая сумма несколько больше, чем при начислении только сложными процентами, кроме того, чем чаще начисляются декурсивные проценты, тем больше наращенная сумма. Значит для кредитора (банка) самым выгодным является последний вариант, а для заемщика (предпринимателя) первый вариант.
Пример 2.4 Вы имеете возможность поместить свои свободные денежные средства в долларах США на 1,5 года в одном банке на валютном депозите под процентную ставку 6% годовых с ежемесячным начислением сложных процентов или в другом банке эту же сумму поместить на рублевом депозите под процентную ставку 10% годовых с полугодовым начислением сложных процентов. Как вам лучше поступить, если курс покупки долларов на начало срока – 29,10 руб., а ожидаемый курс продажи через 1,5 года – 30,10 руб.
Решение. Обозначим имеющееся количество долларов через P. Остальные параметры финансовой операции составят: n=1,5; m$=12; mруб.=2; j$=0,06; jруб.=0,1. Помещая доллары на валютный депозит, через 1,5 года можно получить:
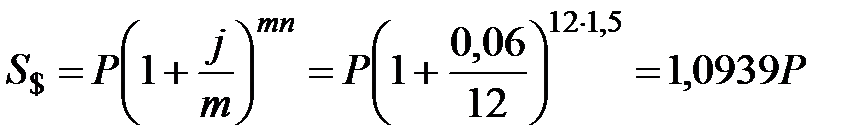 долл. США.
долл. США.
Если же имеющиеся P долларов обменять на рубли, то в соответствии с курсом покупки можно получить 29,1P руб. Через 1,5 года наращенная сумма на рублевом депозите составит:
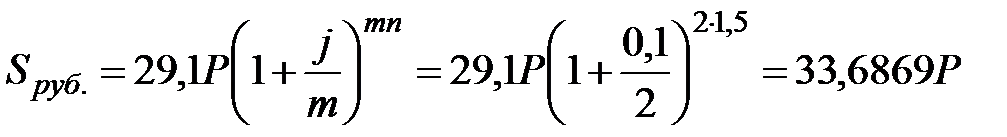 руб.,
руб.,
что при конвертации по ожидаемому курсу продажи даст:
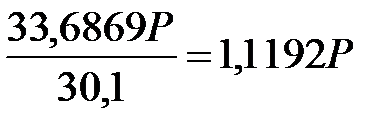 долл. США.
долл. США.
Сравнивая эту величину с наращенной суммой на валютном депозите ( 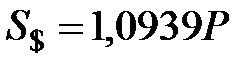 ), делаем вывод, что лучше поместить доллары на рублевый депозит.
), делаем вывод, что лучше поместить доллары на рублевый депозит.
Пример 2.5 На сумму 90 тыс. руб. в течение 3,5 лет ежеквартально начисляются сложные проценты по ставке 14% годовых. За этот же период цены росли ежемесячно в течение первого года на 1%, в течение второго года – на 1,1%, в течение третьего – на 1,3%, последние полгода – на 1,1%. Определить: покупательную способность наращенной суммы через 3,5 года; ставку реальной доходности финансовой операции; минимальную положительную ставку, обеспечивающую реальное наращение капитала. Какова должна быть банковская ставка, которая обеспечит реальную доходность операции 14% годовых при ежеквартальном начислении процентов?
Решение. Имеем: P=90000 руб.; n=3,5 года или 42 месяца, n1=n2=n3=12 месяцев, n4=6 месяцев; h1=1, h2=1,1, h3=1,3, h4=1,1; m=4; j=0,14.
1. Найдем индекс инфляции за 3,5 года или 42 месяца по формуле (2.42)
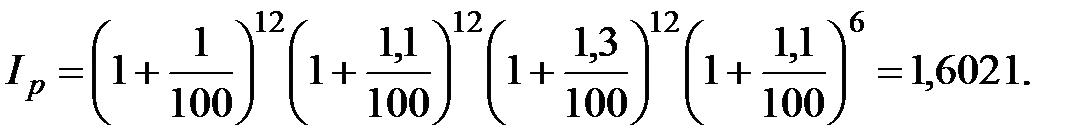
2. Определяем покупательную способность наращенной суммы с учетом инфляции. Так как m=4 (т.е. m>1), то
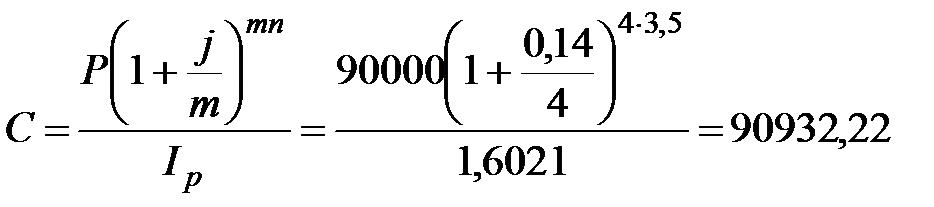 руб.
руб.
Таким образом, реальная наращенная сумма с учетом инфляции оказалась больше первоначальной только на 932,22 руб.
3. Ставка реальной доходности наращения составит:
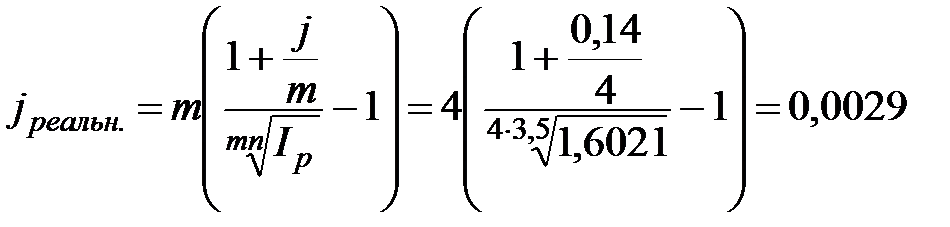 или 0,29%,
или 0,29%,
т.е. при исходных параметрах финансовая операция является малоприбыльной.
4. Минимальная ставка, компенсирующая влияние инфляции составит:
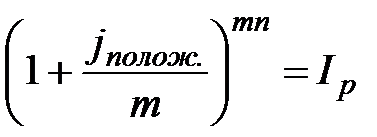 , (2.56)
, (2.56)
откуда 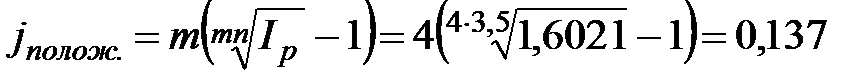 или 13,7%.
или 13,7%.
Таким образом, для обеспечения реального наращения капитала номинальная процентная ставка должна превышать 13,7% годовых при ежеквартальном начислении процентов.
5. Брутто-ставка, обеспечивающая реальную доходность 14% годовых с поквартальным начислением процентов, при данных темпах инфляции будет определяться по формуле:
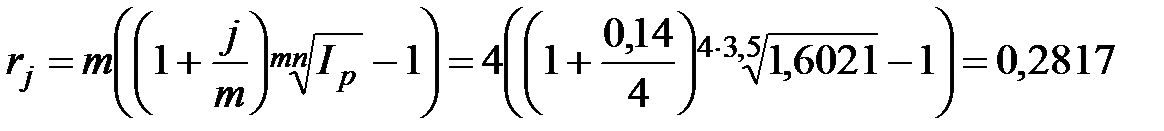 или 28,17%.
или 28,17%.
Это означает, что если банк увеличит номинальную процентную ставку до 28,17% годовых, то влияние инфляции будет полностью компенсировано.
Задачи для самостоятельного решения
2.1 Определенная сумма (таблица 2.3) инвестируется под годовую процентную ставку: а) на 30 дней; б) 80 дней; в) на 3 месяца; г) на 6 месяцев; д) 1 год; е) 5 лет; ж) 8 лет. Найдите наращенные суммы при условии ежегодного начисления сложных и простых процентов.
Таблица 2.3 – Размер инвестируемой суммы и процентная ставка
| Вариант | Ссуда, тыс. руб. | Ставка, % | Вариант | Ссуда, тыс. руб. | Ставка, % |
| 16,0 | 17,4 | ||||
| 18,5 | 15,0 | ||||
| 16,3 | 16,2 | ||||
| 14,9 | 17,0 | ||||
| 15,7 | 15,9 | ||||
| 19,0 | 15,2 | ||||
| 18,0 | 16,4 | ||||
| 14,1 | 15,2 | ||||
| 13,7 | 14,9 | ||||
| 18,2 | 16,4 | ||||
| 19,7 | 14,8 | ||||
| 14,8 | 17,5 | ||||
| 13,7 | 16,9 | ||||
| 15,9 | 15,7 | ||||
| 16,8 | 18,5 |
2.2 Депозит в 400 тыс. руб. положен в банк на 5 лет под процентную ставку 12% годовых. Найдите сумму начисленных процентов и наращенную сумму, если ежегодно начисляются сложные проценты.
2.3 Предприниматель получил в банке ссуду в размере 830 тыс. руб. сроком на 7 лет на следующих условиях: для первых двух лет процентная ставка равна 14% годовых, на следующие три года устанавливается маржа в размере 0,5% и на последующие годы маржа равна 0,8%. Найдите сумму, которую предприниматель должен вернуть в банк по окончании срока ссуды при ежегодном начислении сложных процентов.
2.4 На определенную сумму кредита (таблица 2.4) в течении 8 лет начисляются проценты по соответствующей ставке на следующих условиях: первые 4 года ставка первоначальна, каждые следующие 2 года ставка увеличивается на определенную величину. Определить наращенную к концу срока сумму, если проценты начислялись: один раз в году; ежеквартально; каждые два года.
Таблица 2.4 – Варианты погашения кредита
| Вариант | Сумма, тыс. руб. | Первоначальная ставка, % | Увеличение ставки, % | Вариант | Сумма, тыс. руб. | Первоначальная ставка, % | Увеличение ставки, % |
| 17,4 | 1,1 | 16,0 | 0,8 | ||||
| 15,0 | 0,9 | 18,5 | 1,0 | ||||
| 16,2 | 1,7 | 16,3 | 1,1 | ||||
| 17,0 | 2,1 | 14,9 | 0,7 | ||||
| 15,9 | 0,8 | 15,7 | 1,2 | ||||
| 15,2 | 0,5 | 19,0 | 1,9 | ||||
| 16,4 | 1,0 | 18,0 | 2,0 | ||||
| 15,2 | 1,4 | 14,1 | 0,8 | ||||
| 14,9 | 0,6 | 13,7 | 0,9 | ||||
| 16,4 | 1,9 | 18,2 | 1,0 | ||||
| 14,8 | 1,4 | 19,7 | 1,7 | ||||
| 17,5 | 2,1 | 14,8 | 0,6 | ||||
| 16,9 | 0,5 | 13,7 | 0,9 | ||||
| 15,7 | 0,9 | 15,9 | 0,7 | ||||
| 18,5 | 1,7 | 16,8 | 1,5 |
2.5 Банк предоставил ссуду (таблица 2.5) на 33 месяца на следующих условиях: а) ежегодного начисления процентов; б) ежеквартального начисления процентов; в) полугодичного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока ссуды при использовании схемы сложных процентов и при использовании смешанной схемы? Какая схема менее выгодна для банка?
Таблица 2.5 – Размер ссуды и ставка
| Вариант | Ссуда, тыс. руб. | Ставка, % | Вариант | Ссуда, тыс. руб. | Ставка, % |
| 16,0 | 17,4 | ||||
| 18,5 | 15,0 | ||||
| 16,3 | 16,2 | ||||
| 14,9 | 17,0 | ||||
| 15,7 | 15,9 | ||||
| 19,0 | 15,2 | ||||
| 18,0 | 16,4 | ||||
| 14,1 | 15,2 | ||||
| 13,7 | 14,9 | ||||
| 18,2 | 16,4 | ||||
| 19,7 | 14,8 |
Продолжение таблицы 2.5
| Вариант | Ссуда, тыс. руб. | Ставка, % | Вариант | Ссуда, тыс. руб. | Ставка, % |
| 14,8 | 17,5 | ||||
| 13,7 | 16,9 | ||||
| 15,9 | 15,7 | ||||
| 16,8 | 18,5 |
2.6 Банк предоставил ссуду (таблица 2.6) на 37 месяцев под процентную ставку 20% годовых на условиях единовременного возврата основной суммы долга и начислении сложных процентов. Какую сумму предстоит вернуть банку, если проценты начисляются а) ежегодно; б) по полугодиям; в) ежеквартально. Используйте схему сложных процентов и смешанную схему.
Таблица 2.6 – Размер предоставленной ссуды
| Вариант | Ссуда, тыс. руб. | Вариант | Ссуда, тыс. руб. |
2.7 Предприниматель взял в банке ссуду (таблица 2.7) под сложную процентную ставку 16% годовых. Через 2 года и 7 месяцев кредит был погашен. Определите наращенную сумму кредита, если проценты начислялись а) ежегодно; б) по полугодиям; в) каждые два месяца; г) ежеквартально; в) ежемесячно.
Таблица 2.7 – Размер кредита
| Вариант | Ссуда, тыс. руб. | Вариант | Ссуда, тыс. руб. |
Продолжение таблицы 2.7
| Вариант | Ссуда, тыс. руб. | Вариант | Ссуда, тыс. руб. |
2.8 В банк вложены деньги в сумме (таблица 2.8) на определенный срок под процентную ставку г с ежеквартальным начислением сложных процентов. Определите наращенную сумму и проценты. Как изменится итоговая наращенная сумма и сумма процентов при ежемесячном и полугодовом начислении сложных процентов? Какой вывод можно сделать о частоте начисления сложных процентов?
Таблица 2.8 – Размер вклада и ставка
| Вариант | Вклад, тыс. руб. | Ставка, % | Вариант | Вклад, тыс. руб. | Ставка, % |
| 10,0 | 7,4 | ||||
| 11,5 | 10,0 | ||||
| 10,3 | 9,2 | ||||
| 10,9 | 11,0 | ||||
| 9,7 | 8,9 | ||||
| 9,0 | 11,2 | ||||
| 8,0 | 10,4 | ||||
| 10,1 | 10,2 | ||||
| 10,7 | 10,9 | ||||
| 11,2 | 11,4 | ||||
| 10,7 | 10,8 | ||||
| 11,8 | 10,5 | ||||
| 10,7 | 10,9 | ||||
| 10,9 | 9,7 | ||||
| 10,8 | 11,5 |
2.9 На вклад в конце каждого полугодия начисляются сложные проценты по номинальной годовой процентной ставке 10%. За какой срок первоначальный капитал увеличится в четыре раза? Как изменится результат, если сложные проценты начисляются ежемесячно?
2.10 За какой срок исходная первоначальная сумма возрастет до заданной (таблица 2.9), если сложные проценты по ставке 11% годовых начисляются: а) ежегодно; б) по полугодиям; в) ежеквартально; г) каждые два месяца; д) ежемесячно?
Таблица 2.9 – Первоначальная сумма и сумма возврата
| Вариант | Первоначальная сумма, тыс. руб. | Сумма возврата, тыс. руб. | Вариант | Первоначальная сумма, тыс. руб. | Сумма возврата, тыс. руб. |
2.11 Вы имеете на счете определенную сумму (таблица 2.10) и хотели бы удвоить эту сумму через пять лет. Какое значение сложной процентной ставки удовлетворяет заданным условиям при: а) ежегодном начислении процентов; б) полугодичном начислении; в) ежеквартальном начислении; г) ежемесячном начислении.
Таблица 2.10 – Размер суммы на счете
| Вариант | Сумма на счете, тыс. руб. | Вариант | Сумма на счете, тыс. руб. |
2.12 Вкладчик хотел бы за 6 лет удвоить сумму, помещаемую в банк на депозит. Какую годовую номинальную процентную ставку должен предложить банк при начислении сложных процентов ежеквартально?
2.13 Вы имеете возможность получить кредит либо на условиях 17% годовых с ежемесячным начислением сложных процентов, либо на условиях 19% годовых с ежеквартальным начислением сложных процентов. Какой вариант предпочтительнее?
2.14 На вашем счете в банке 80 тыс. руб. Банк платит 10% годовых. Вам предлагают принять участие всем вашим капиталом в некоторой финансовой сделке. Представленные экономические расчеты показывают, что в случае согласия через пять лет ваш капитал возрастет до 140 тыс. руб. Стоит ли принимать это предложение?
2.15 Клиент поместил в банк 250 тыс. руб. на условиях начисления сложных процентов по процентной ставке 10% годовых. Через 1 год 9 месяцев клиент снял со счета 80 тыс. руб., еще через 3 года положил на свой счет 40 тыс. руб., а после этого через 2 года 3 месяца он закрыл счет. Определите сумму, полученную клиентом при закрытии счета.
2.16 Господин N поместил в банк 300 тыс. руб. на условиях начисления ежеквартально сложных процентов по годовой номинальной процентной ставке 9%. Через 3 года 3 месяца господин N снял со счета 120 тыс. руб., еще через 1 год 6 месяцев положил на свой счет 80 тыс. руб., а после этого через 15 месяцев он закрыл счет. Определите сумму, полученную господином N при закрытии счета.
2.17 Вкладчик может свои свободные денежные средства в долларах на один год поместить в одном банке на валютном депозите под процентную ставку 7% годовых с полугодовым начислением сложных процентов или в другом банке эту же сумму поместить на рублевом депозите под процентную ставку 10% годовых с ежеквартальным начислением сложных процентов. Как ему лучше поступить, если курс покупки долларов на начало срока – 31 руб. 80 коп., а ожидаемый курс продажи через год – 30 руб. 50 коп.?
2.18 По условиям финансового контракта на депозит (таблица 2.11), положенный в банк на 5 лет, начисляются проценты по сложной учетной ставке. Определите наращенную сумму, если начисление процентов производится: а) ежегодно; б) каждое полугодие; в) ежеквартально; г) каждые два месяца; д) ежемесячно. Сравните полученные величины с результатами наращения сложными процентами по процентной ставке.
Таблица 2.11 – Размер вклада и ставка
| Вариант | Вклад, тыс. руб. | Ставка, % | Вариант | Вклад, тыс. руб. | Ставка, % |
| 10,0 | 7,4 | ||||
| 11,5 | 10,0 | ||||
| 10,3 | 9,2 | ||||
| 10,9 | 11,0 | ||||
| 9,7 | 8,9 | ||||
| 9,0 | 11,2 | ||||
| 8,0 | 10,4 | ||||
| 10,1 | 10,2 |
Продолжение таблицы 2.11
| Вариант | Вклад, тыс. руб. | Ставка, % | Вариант | Вклад, тыс. руб. | Ставка, % |
| 10,7 | 10,9 | ||||
| 11,2 | 11,4 | ||||
| 10,7 | 10,8 | ||||
| 11,8 | 10,5 | ||||
| 10,7 | 10,9 | ||||
| 10,9 | 9,7 | ||||
| 10,8 | 11,5 |
2.19 Сроком на 6 лет выпущена облигация номиналом 10000 руб., причем предусмотрен следующий порядок начисления сложных процентов по плавающей годовой учетной ставке: первые три года – 12% годовых, в последующие два года – 16% годовых и в оставшийся год – 18% годовых. Найдите наращенную сумму.
2.20 Вексель был учтен за 21 месяц до срока погашения, при этом владелец векселя получил 80% от написанной на векселе суммы. По какой сложной годовой учетной ставке был учтен этот вексель?
2.21 Вы имеете вексель на сумму (таблица 2.12) и хотели бы при его учете по сложной учетной ставке за 2 года до срока погашения получить две трети этой суммы. Какая должна быть годовая номинальная учетная ставка при дисконтировании поквартально? Как изменится ответ, если дисконтирование осуществляется раз в год?
Таблица 2.12 – Размер суммы на счете
| Вариант | Сумма, руб. | Вариант | Сумма, руб. |
2.22 3а какое время до срока погашения был учтен вексель на сумму 500 тыс. руб., если предъявитель векселя получил 350 тыс. руб., а дисконтирование по номинальной учетной ставке 14% годовых производилось: а) поквартально; б) помесячно?
2.23 Из какого капитала можно получить сумму (таблица 2.13) через 4 года при наращением по сложной процентной ставке 11% годовых, если наращение осуществлять: а) ежегодно; б) по полугодиям; в)ежеквартально; г) каждые два месяца; д) ежемесячно; е) каждые полмесяца?
Таблица 2.13 – Размер суммы на счете
| Вариант | Сумма на счете, руб. | Вариант | Сумма на счете, руб. |
2.24 Банк начисляет ежеквартально сложные проценты по годовой номинальной процентной ставке 10%. Определите современную ценность денежной суммы (таблица 2.14), которая должна быть выплачена через: а)1 год 2 месяца; б) 3 года 3 месяца; в) 5 лет 9 месяцев; в) 7 лет 4 месяца. Как изменится современная сумма если проценты будут начисляться ежемесячно?
Таблица 2.14 – Размер суммы на счете
| Вариант | Сумма на счете, руб. | Вариант | Сумма на счете, руб. |
2.25 Наращенная к концу седьмого года сумма составит 840 тыс. руб. Найдите ее современное значение, если начисляются сложные проценты: а) по полугодиям по процентной ставке 10% годовых; б) ежеквартально по процентной ставке 15% годовых.
2.26 Долговое обязательство на выплату 420 тыс. руб. со сроком погашения через 5 лет учтено за 3 года до срока с дисконтом по сложной учетной ставке 14% годовых. Найдите величину дисконта. Как изменится величина дисконта, если долговое обязательство учтено сразу после его выдачи?
2.27 Долговое обязательство на выплату 200 тыс. руб. со сроком погашения через 6 лет учтено за три года до срока. Определите полученную сумму и дисконт, если дисконтирование производилось: а) полугодовое; б) поквартальное; в) помесячное по номинальной учетной ставке 18% годовых.
2.28 Определите современное значение суммы в 800 тыс. руб., если она будет выплачена через 4 года 9 месяцев и дисконтирование производится по полугодиям по номинальной годовой учетной ставке 15%.
2.29 Клиент поместил в банк сумму (таблица 2.15) сроком на: а). 2 года; б) 3 года; в) 4 года. Какая сумма будет на счете клиента, если банк начисляет сложные проценты: а) по номинальной процентной ставке 11,5% годовых с полугодовым начислением процентов; б) по номинальной учетной ставке 11,5% годовых с ежеквартальным начислением процентов; в) по непрерывной ставке с силой роста 11,5% за год?
Таблица 2.15 – Размер суммы на счете
| Вариант | Сумма на счете, тыс. руб. | Вариант | Сумма на счете, тыс. руб. |
2.30 Какую сумму необходимо поместить на банковский депозит, чтобы через 5 лет получить 680 тыс. руб., если происходит непрерывное начисление процентов по ставке 12%?
2.31 За какой срок сумма 500 тыс. руб. достигнет величины 900 тыс. руб. при непрерывном начислении процентов и силе роста 14%? Как изменится ответ при начислении сложных процентов ежеквартально по номинальной процентной ставке 14% годовых?
2.32 Под какую непрерывную ставку можно поместить деньги на депозит, если первоначальная сумма сейчас эквивалентны определенной наращенной сумме (таблица 2.16) через: 2 года; 5 лет; 8 лет? Какая сложная процентная ставка с начислением процентов по полугодиям решает эту задачу?
Таблица 2.16 – Сумма выдачи и возврата кредита
| Вариант | Первоначальная сумма, тыс. руб. | Наращенная сумма, тыс. руб. | Вариант | Первоначальная сумма, тыс. руб. | Наращенная сумма, тыс. руб. |
2.33 Определите наращенную сумму (таблица 2.17) сроком за: 1 год; 2 года; 3 года; 4 года, если начальное значение силы роста составляет 9%, процентная ставка непрерывно и линейно увеличивается со скоростью 2% в год.
Таблица 2.17 – Размер первоначальной суммы
| Вариант | Сумма, тыс. руб. | Вариант | Сумма, тыс. руб. |
2.34 Определите современную стоимость 500 тыс. руб., которые должны быть выплачены через 5 лет, если начальное значение силы роста составляет 7%, процентная ставка непрерывно и линейно изменяется со скоростью 1,5% в год.
2.35 Определите начальное значение силы роста, необходимое для увеличения начального капитала в 3 раза за 8 лет, если процентная ставка непрерывно и экспоненциально увеличивается с постоянным темпом прироста 2% в год.
2.36 Среднемесячный темп прироста инфляции в течение года составлял 1,5%. Определите индекс и темп прироста инфляции: а) за квартал; б) за полгода; в) за год.
2.37 Клиент поместил в банк сумму (таблица 2.18) на определенный срок. Определите наращенную величину вклада, если начальный уровень силы роста 10%, процентная ставка непрерывно и экспоненциально увеличивается с постоянным темпом прироста 1,5% в год.
Таблица 2.18 – Размер суммы на счете
| Вариант | Сумма на счете, тыс. руб. | Срок, лет. | Вариант | Сумма на счете, тыс. руб. | Срок, лет. |
2.38 Определите современную стоимость 780 тыс. руб., которые должны быть выплачены через 6 лет, если начальный уровень силы роста 9,5%, процентная ставка непрерывно и экспоненциально увеличивается с постоянным темпом прироста 0,7% в год.
2.37 За какой срок произойдет: а) удвоение капитала; б) увеличение в 2,5 раза; в) увеличение в 3 раза; г) увеличение в 4 раза; если начальный уровень силы роста (таблица 2.19), процентная ставка непрерывно и экспоненциально увеличивается с постоянным темпом прироста в год.
Таблица 2.19 – Размер суммы на счете
| Вариант | Начальный уровень силы роста, % | Темп прироста в год, % | Вариант | Начальный уровень силы роста, % | Темп прироста в год, % |
| 10,0 | 3,0 | 11,9 | 1,7 | ||
| 13,8 | 2,0 | 11,6 | 2,8 | ||
| 12,8 | 1,5 | 12,3 | 2,2 | ||
| 14,7 | 2,1 | 10,8 | 1,1 | ||
| 12,0 | 1,8 | 14,0 | 1,2 | ||
| 11,9 | 3,1 | 13,7 | 3,2 | ||
| 12,8 | 1,3 | 14,2 | 1,5 | ||
| 13,6 | 2,2 | 12,7 | 2,4 | ||
| 14,7 | 2,0 | 13,4 | 1,6 | ||
| 14,1 | 3,0 | 12,4 | 3,0 | ||
| 15,1 | 1,4 | 13,1 | 2,0 | ||
| 14,2 | 2,3 | 11,9 | 3,1 | ||
| 14,9 | 2,2 | 14,6 | 1,6 | ||
| 14,2 | 3,0 | 13,9 | 1,7 | ||
| 13,2 | 2,3 | 11,9 | 1,9 |
2.40 По данным таблицы 2.20 определить индекс инфляции за:
а) полгода;
б) год;
в) полтора года;
г) два года.
Таблица 2.20 – Темп прироста инфляции
| Вариант | Инфляция, % | Число раз прироста инфляции в течение года | Вариант | Инфляция, % | Число раз прироста инфляции в течение года | ||
| 0,8 | 2,0 | ||||||
| 1,0 | 2,5 | ||||||
| 0,9 | 2,1 | ||||||
| 1,2 | 1,7 | ||||||
| 1,3 | 0,9 | ||||||
| 0,7 | 2,4 | ||||||
| 0,8 | 2,7 | ||||||
| 1,4 | 3,0 | ||||||
| 0,9 | 2,1 | ||||||
| 0,6 | 0,9 | ||||||
| 1,0 | 2,8 | ||||||
1,
Дата добавления: 2014-09-08; просмотров: 2106; Нарушение авторских прав 
Мы поможем в написании ваших работ! |