
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
КОНСОЛИДАЦИЯ ПЛАТЕЖЕЙ
Для наращения и дисконтирования денежных сумм могут применяться различные виды процентных ставок. Часто требуется определить ставки, которые в конкретных условиях приводят к одинаковым финансовым результатам, когда замена одного вида ставки на другой, при соблюдении принципа эквивалентности, не изменяет финансовых отношений сторон в рамках одной операции.
Процентные ставки, обеспечивающие равноценность финансовых последствий называются эквивалентными.Эквивалентность ставок обеспечивается равенством множителей наращения или дисконтных множителей.
Таблица 3.1 – Эквивалентность процентных ставок
| № п/п | Вид ставки | Формула эквивалентности | |||
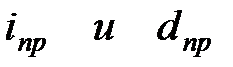
| Срок сделки выражен в годах (n) | ||||
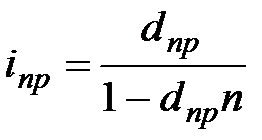 (3.1) (3.1)
| 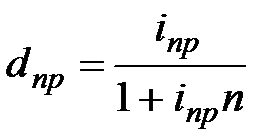 (3.2) (3.2)
| ||||
| Срок сделки выражен в месяцах (m) | |||||
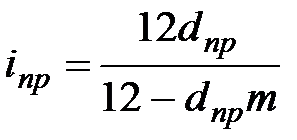 (3.3) (3.3)
| 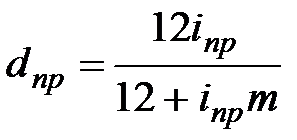 (3.4) (3.4)
| ||||
| Срок сделки выражен в днях (временная база для обеих ставок 360 дней) | |||||
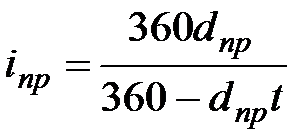 (3.5) (3.5)
| 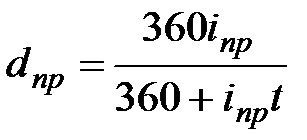 (3.6) (3.6)
| ||||
| Срок сделки выражен в днях (временная база для процентной ставки 365 дней, а для учетной ставки 360 дней) | |||||
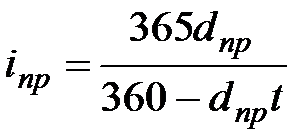 (3.7) (3.7)
| 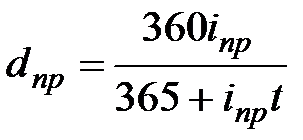 (3.8) (3.8)
| ||||
Продолжение таблицы 3.1
| № п/п | Вид ставки | Формула эквивалентности | |

| 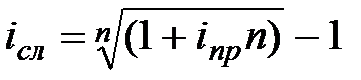 (3.9) (3.9)
| 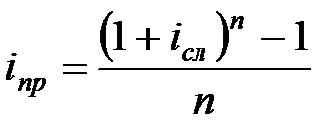 (3.10) (3.10)
| |
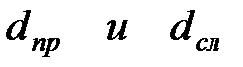
| 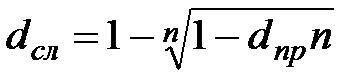 (3.11) (3.11)
| 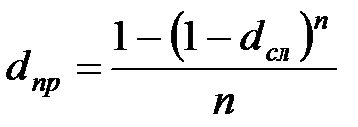 (3.12) (3.12)
| |
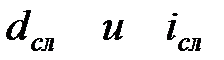
| 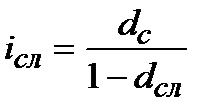 (3.13) (3.13)
| 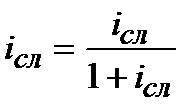 (3.14) (3.14)
| |
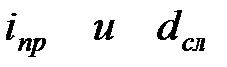
| 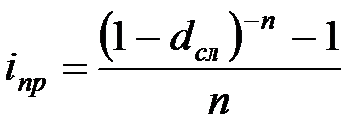 (3.15) (3.15)
|  (3.16) (3.16)
| |
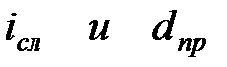
| 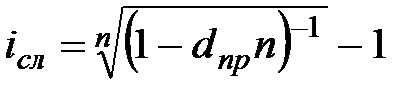 (3.17) (3.17)
| 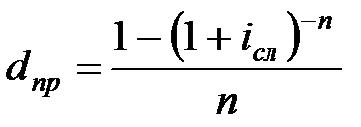 (3.18) (3.18)
| |
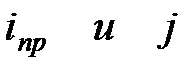
| 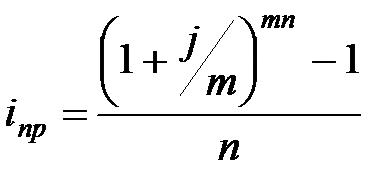 (3.19) (3.19)
| 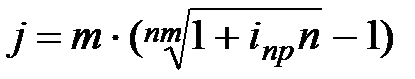 (3.20 (3.20
| |
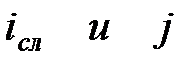
| 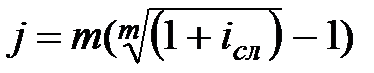 (3.21) (3.21)
|  (3.22) (3.22)
| |
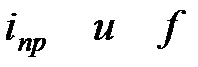
| 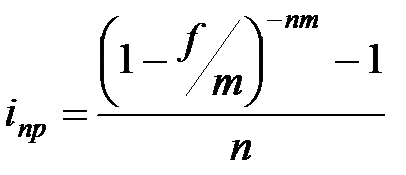 (3.23) (3.23)
| 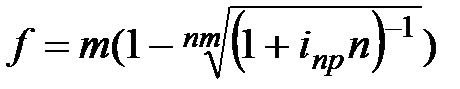 (3.24) (3.24)
| |
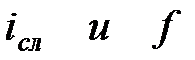
| 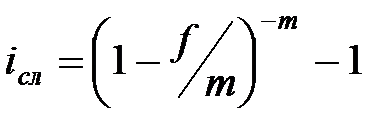 (3.25) (3.25)
| 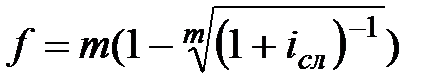 (3.26) (3.26)
| |
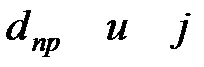
| 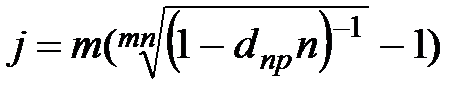 (3.27) (3.27)
| 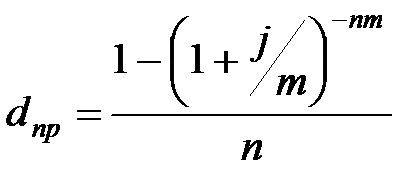 (3.28) (3.28)
| |
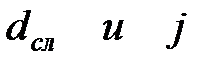
| 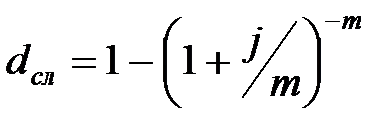 (3.29) (3.29)
| 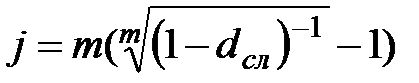 (3.30) (3.30)
| |
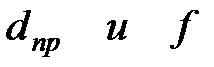
| 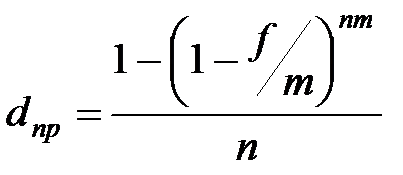 (3.31) (3.31)
| 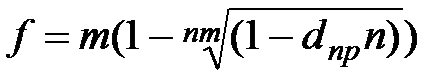 (3.32) (3.32)
| |
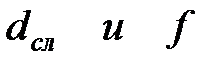
| 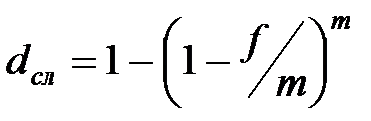 (3.33) (3.33)
| 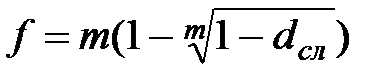 (3.34) (3.34)
| |
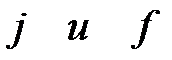
| 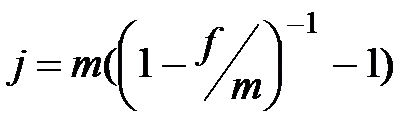 (3.35) (3.35)
| 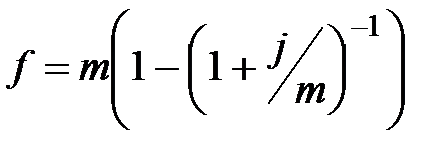 (3.36) (3.36)
|
Пример 3.1 Вексель учтен за год до даты его погашения по учетной ставке 15,0 %. Какова доходность учетной операции в виде процентной ставки?
Решение.
По формуле 3.1 находим:
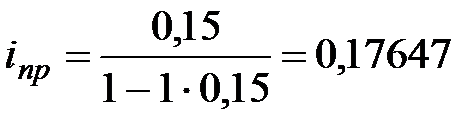 , или 17,647%.
, или 17,647%.
Пример 3.2 Какой сложной годовой ставкой можно заменить в контракте простую ставку 18% (K=365), не изменяя финансовых последствий? Срок операции 580 дней.
Решение.
Находим эквивалентную сложную ставку по формуле 3.9
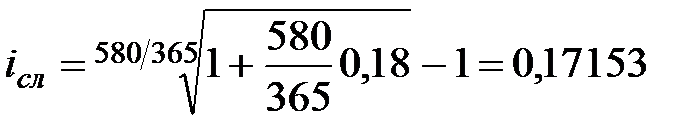 или 17,153%.
или 17,153%.
Пример 3.3 При разработке условий контракта стороны договорились о том, что доходность кредита должна составлять 28% годовых. Каков должен быть размер номинальной ставки при начислении процентов ежемесячно, поквартально?
Решение.
Воспользуемся формулой 3.20:
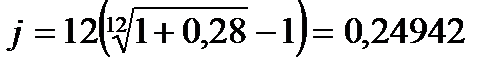 ;
;  .
.
Если в финансовой операции размер процентной ставки изменяется во времени, то все значения ставки можно обобщить с помощью средней.
Пусть за периоды 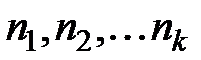 начисляются простые проценты по ставкам
начисляются простые проценты по ставкам 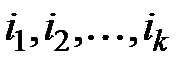 .
.
Средние процентные ставки получим посредством приравнивания соответствующих множителей наращения друг к другу: 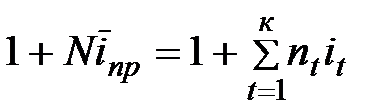 ,
,
отсюда 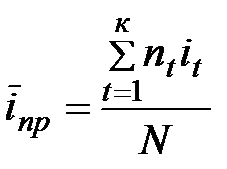 .
.
Аналогично получим 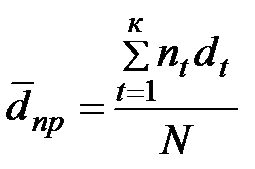 , (3.37)
, (3.37)
где N = 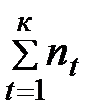 - общий срок наращения процентов,
- общий срок наращения процентов,
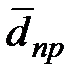 и
и 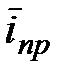 - средняя учетная и процентная ставка.
- средняя учетная и процентная ставка.
Если изменяются во времени и первоначальные суммы, то 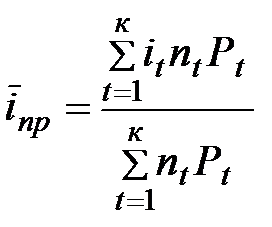 .(3.38)
.(3.38)
Если усредняются переменные во времени ставки сложных процентов, то:
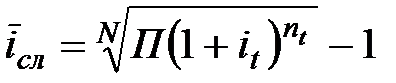 ; (3.39)
; (3.39)
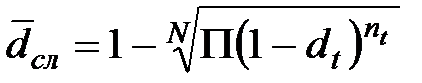 . (3.40)
. (3.40)
Пример 3.4 Для первых двух лет ссуды применяется ставка 20%, для следующих трех лет она составляет 24%. Нужно найти среднюю ставку.
Решение.
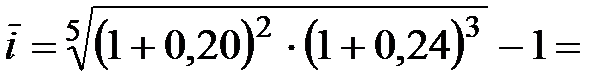 0,22384, или 22,384%.
0,22384, или 22,384%.
Иногда меняются только суммы ссуд и проценты, а сроки операций равны.
Если применяются простые проценты, то 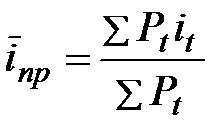 . (3.41)
. (3.41)
Когда усредняются сложные процентные ставки, то средняя ставка составит
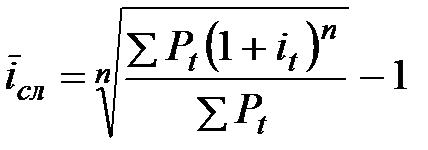 . (3.42)
. (3.42)
Часто возникает необходимость изменения условий ранее заключенных сделок: изменение сроков платежей, объединение нескольких платежей в один – консолидация платежей.
Пусть платежи 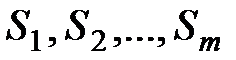 со сроками выплат
со сроками выплат 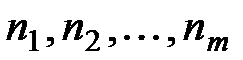 заменяются одним в сумме
заменяются одним в сумме 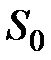 и сроком
и сроком 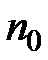 . В этом случае возможны две постановки задачи: если задается срок
. В этом случае возможны две постановки задачи: если задается срок 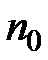 , то находится сумма
, то находится сумма 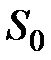 , и наоборот, если задана сумма консолидированного платежа, то определяется его срок.
, и наоборот, если задана сумма консолидированного платежа, то определяется его срок.
Определение размера платежа.
1) Если используется простая процентная ставка, а сроки объединяемых платежей меньше срока консолидированного платежа, то
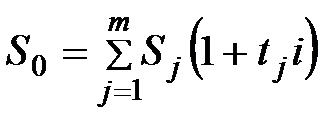 , (3.43)
, (3.43)
где  - размеры объединяемых платежей со сроками
- размеры объединяемых платежей со сроками 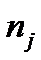 <
< 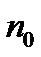 .
.
2) Если используется простая процентная ставка, а сроки объединяемых платежей как меньше, так и больше срока консолидированного платежа, то
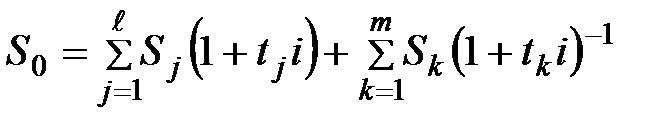 , (3.44)
, (3.44)
где Sj – размеры платежей со сроками погашения nj < no, 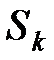 - размеры платежей со сроками
- размеры платежей со сроками 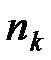 >
> 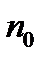 ,
, 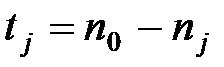 ,
, 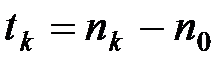 .
.
3) Если используется простая учетная ставка, а сроки объединяемых платежей меньше срока консолидированного платежа, то
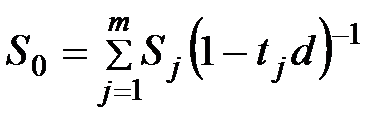 . (3.45)
. (3.45)
4) Если используется простая учетная ставка, а сроки объединяемых платежей как меньше, так и больше срока консолидированного платежа, то
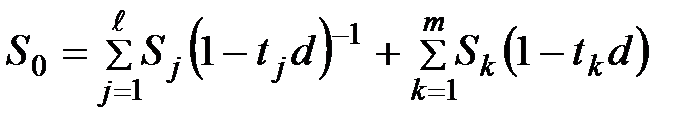 . (3.46)
. (3.46)
5) Если используется сложная процентная ставка, а сроки объединяемых платежей меньше срока консолидированного платежа:
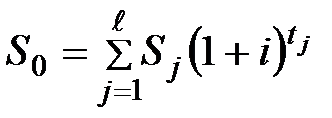 , при no > nj. (3.47)
, при no > nj. (3.47)
6) Если используется сложная процентная ставка, а сроки объединяемых платежей как меньше, так и больше срока консолидированного платежа:
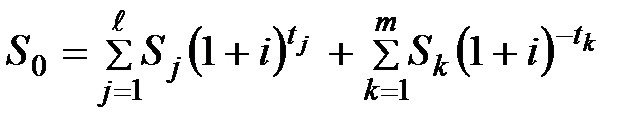 , при nj < no < nк . (3.48)
, при nj < no < nк . (3.48)
7) Если используется сложная учетная ставка, а сроки объединяемых платежей меньше срока консолидированного платежа, то
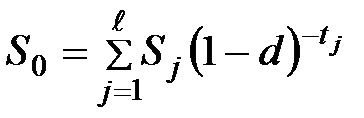 . (3.49)
. (3.49)
8) Если используется сложная учетная ставка, а сроки объединяемых платежей как меньше, так и больше срока консолидированного платежа:
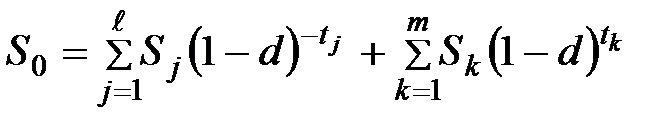 . (3.50)
. (3.50)
Определение срока консолидированного платежа.
При начислении простых процентов срок консолидированного платежа no находится по формуле:
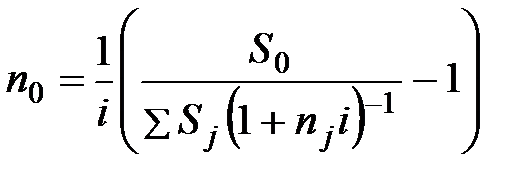 =
= 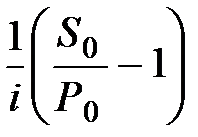 , (3.51)
, (3.51)
где Р0 – современная стоимость консолидируемых платежей,
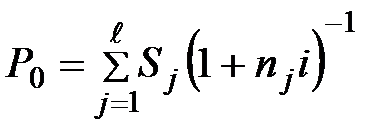 . (3.52)
. (3.52)
При использовании сложных процентов:
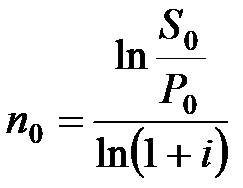 , (3.53)
, (3.53)
где 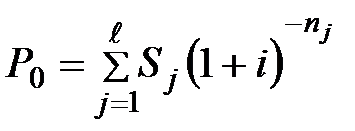 . (3.54)
. (3.54)
Эквивалентность сложных дискретных и непрерывных ставок.
Обозначим силу роста через – b.
Эквивалентность сложной процентной ставки и силы роста:
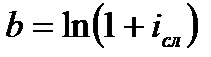 ;
; 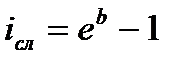 . (3.55)
. (3.55)
Эквивалентность номинальной процентной ставки и силы роста:
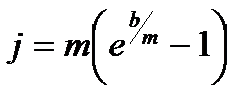 ;
; 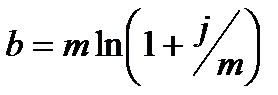 . (3.56)
. (3.56)
Эквивалентность силы роста и учетной ставки:
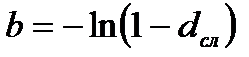 ;
; 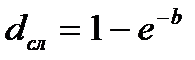 ;
; 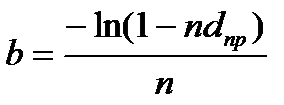 ;
;  . (3.57)
. (3.57)
Задачи для самостоятельного решения
3.1 Определите:
- простую процентную ставку, если кредит выдан по простой учетной ставке;
- простую учетную ставку, если кредит выдан по простой процентной ставке;
- сложную учетную ставку, если кредит выдан по сложной процентной ставке;
- сложную процентную ставку, если кредит выдан по сложной учетной ставке;
- простую процентную ставку, если кредит выдан по сложной процентной ставке;
- сложную процентную ставку, если кредит выдан по простой процентной ставке;
- простую учетную ставку, если кредит выдан по сложной учетной ставке;
- сложную учетную ставку, если кредит выдан по простой учетной ставке;
- сложную процентную ставку, если кредит выдан по простой учетной ставке;
- простую учетную ставку, если кредит выдан по сложной процентной ставке;
- сложную учетную ставку, если кредит выдан по простой процентной ставке;
- простую процентную ставку, если кредит выдан по сложной учетной ставке.
Таблица 3.2 – Выдача кредитов
| Вари- ант | Срок предоставления кредита | Процентная ставка, % | Вари- ант | Срок предоставления кредита | Процентная ставка, % |
| 2 года | 10,0 | 4 года | 20,0 | ||
| 3 месяца | 11,0 | 240 дней | 19,0 | ||
| 120 дней | 10,5 | 5 месяцев | 19,5 | ||
| 1 год | 11,5 | 5 лет | 15,5 |
Продолжение таблицы 3.2
| Вари- ант | Срок предоставления кредита | Процентная ставка, % | Вари- ант | Срок предоставления кредита | Процентная ставка, % |
| 9 месяцев | 11,9 | 300 дней | 16,5 | ||
| 200 дней | 10,3 | 13 месяцев | 16,0 | ||
| 4 года | 12,0 | 3 года | 17,0 | ||
| 320 дней | 12,5 | 6 месяцев | 17,5 | ||
| 4 месяца | 12,8 | 320 дней | 17,9 | ||
| 3 года | 13,0 | 4 года | 15,8 | ||
| 90 дней | 13,5 | 8 месяцев | 18,0 | ||
| 7 месяцев | 13,2 | 270 дней | 18,5 | ||
| 2 года | 14,0 | 3 года | 17,1 | ||
| 180 дней | 14,5 | 11 месяцев | 16,7 | ||
| 5 лет | 15,0 | 190 дней | 12,3 |
3.2 Какая сложная процентная ставка соответствует номинальной процентной ставке в размере (таблица 3.3) при начислении процентов 2 раза в месяц; 3 раза в месяц; 4 раза в месяц; 6 раз в месяц при сроке 1 год и 2 года.
Таблица 3.3 – Номинальная процентная ставка
| Вари- ант | Процентная ставка, % | Вари- ант | Процентная ставка, % |
| 9,0 | 12,0 | ||
| 8,0 | 13,0 | ||
| 9,5 | 12,5 | ||
| 10,5 | 13,5 | ||
| 10,9 | 12,1 | ||
| 11,3 | 11,8 | ||
| 11,0 | 11,6 | ||
| 8,5 | 12,1 | ||
| 9,8 | 11,9 | ||
| 10,1 | 12,8 | ||
| 10,7 | 12,2 | ||
| 10,2 | 12,3 | ||
| 11,1 | 14,1 | ||
| 11,5 | 13,7 | ||
| 10,6 | 12,9 |
3.3 Банк принимает депозиты на 1 год с ежеквартальным начислением процентов по ставке 12,0 %, с полугодовым начислением процентов по ставке 13,0 % годовых и с ежегодным начислением процентов по ставке 14,0 % годовых. Определите наилучший вариант вложения средств (определить сложную процентную ставку, при известной номинальной процентной ставке в первом и втором варианте, и результат сравнить со сложной процентной ставкой).
3.4 Вексель учтен в банке до даты погашения за: 60 дней; 90 дней; 120 дней; 180 дней; 7 месяца; 9 месяцев; 11 месяцев по учетной ставке (таблица 3.4). Какова ставка простых процентов, дающая такой же доход?
Таблица 3.4 – Величина учетной ставки
| Вари- ант | Процентная ставка, % | Вари- ант | Процентная ставка, % |
| 9,0 | 12,0 | ||
| 8,0 | 13,0 | ||
| 9,5 | 12,5 | ||
| 10,5 | 13,5 | ||
| 10,9 | 12,1 | ||
| 11,3 | 11,8 | ||
| 11,0 | 11,6 | ||
| 8,5 | 12,1 | ||
| 9,8 | 11,9 | ||
| 10,1 | 12,8 | ||
| 10,7 | 12,2 | ||
| 10,2 | 12,3 | ||
| 11,1 | 14,1 | ||
| 11,5 | 13,7 | ||
| 10,6 | 12,9 |
3.5 Определите значение простой учетной ставки, эквивалентной ставке простых процентов, равной (таблица 3.5) годовых, при сроке ссуды: 90 дней, 120 дней, 150 дней, 6 месяца, 8 месяцев, 11 месяцев.
Таблица 3.5 – Величина простой процентной ставки
| Вари- ант | Процентная ставка, % | Вари- ант | Процентная ставка, % |
| 13,0 | 12,8 | ||
| 11,0 | 12,1 | ||
| 11,5 | 14,5 | ||
| 12,5 | 15,5 | ||
| 11,9 | 14,1 | ||
| 10,3 | 14,8 | ||
| 10,0 | 15,6 | ||
| 8,9 | 15,1 | ||
| 9,5 | 14,9 | ||
| 10,7 | 16,8 | ||
| 10,8 | 16,2 | ||
| 13,2 | 17,3 | ||
| 13,1 | 18,1 | ||
| 13,5 | 17,7 | ||
| 10,6 | 12,9 |
3.6 Клиент имеет в банке счет, по которому: каждые два месяца; ежеквартально и ежемесячно в течение: 2 лет, 3 лет; 5 лет начисляются сложные проценты по номинальной ставке (таблица 3.6). Определите эквивалентную:
- простую процентную ставку;
- простую учетную ставку;
- сложную процентную ставку;
- сложную учетную ставку.
Таблица 3.6 – Величина годовой номинальной процентной ставки
| Вари- ант | Процентная ставка, % | Вари- ант | Процентная ставка, % |
| 8,0 | 8,8 | ||
| 9,0 | 9,1 | ||
| 7,5 | 10,5 | ||
| 9,5 | 12,5 | ||
| 10,9 | 14,1 | ||
| 11,3 | 14,8 | ||
| 10,0 | 11,6 | ||
| 8,9 | 12,1 | ||
| 9,8 | 11,9 | ||
| 10,7 | 10,8 | ||
| 10,1 | 11,2 | ||
| 13,2 | 12,3 | ||
| 11,1 | 7,7 | ||
| 11,5 | 11,7 | ||
| 10,6 | 12,6 |
3.7 Кредит выдан по номинальной процентной ставке.
Таблица 3.7 – Условия предоставления кредита по вариантам
| Вари- ант | Ставка, % | Число раз начислений процентов в году (m) | Срок кредита | Вари- ант | Ставка, % | Число раз начислений процентов в году (m) | Срок кредита |
| 10,9 | 100 дней | 10,5 | 4 месяца | ||||
| 23,0 | 10 месяцев | 10,0 | 6 лет | ||||
| 21,5 | 2 года | 12,4 | 240 дней | ||||
| 24,3 | 3 года | 12,8 | 9 месяцев | ||||
| 20,7 | 1 год | 13,7 | 5 лет | ||||
| 18,9 | 120 дней | 13,9 | 7 месяцев | ||||
| 17,3 | 90 дней | 15,8 | 220 дней | ||||
| 13,8 | 3 месяца | 13,1 | 6 лет | ||||
| 20,9 | 11 месяцев | 19,7 | 270 дней | ||||
| 14,5 | 4 года | 18,5 | 13 месяцев | ||||
| 12,3 | 5 лет | 8,3 | 10 лет | ||||
| 13,2 | 180 дней | 16,8 | 5 месяцев |
Продолжение таблицы 3.7
| Вари- ант | Ставка, % | Число раз начислений процентов в году (m) | Срок кредита | Вари- ант | Ставка, % | Число раз начислений процентов в году (m) | Срок кредита |
| 11,2 | 6 месяцев | 17,9 | 210 дней | ||||
| 9,5 | 5 лет | 16,3 | 5 лет | ||||
| 11,4 | 200 дней | 14,7 | 300 дней |
Определите эквивалентную:
- простую процентную ставку;
- простую учетную ставку;
- сложную процентную ставку;
- сложную учетную ставку;
- номинальную учетную ставку.
3.8 Банк при выдаче ссуды сроком на 3,5 года использовал номинальную процентную ставку в размере 18,3 % годовых, при: а) ежеквартальной; б) полугодовой; в) ежемесячной капитализации процентов. Определите эквивалентную учетную ставку простых и сложных процентов.
3.9 Определите номинальную ставку сложных процентов при начислении процентов: а) каждые два месяца; б) ежеквартально; в) полугодичном; г) ежемесячном, эквивалентную сложной учетной ставке в размере 18,7 %.
3.10 Кредит выдан по номинальной учетной ставке по следующим условиям.
Таблица 3.8 – Условия предоставления кредита по вариантам
| Вари- ант | Ставка, % | Число раз начислений процентов в году (m) | Срок кредита | Вари- ант | Ставка, % | Число раз начислений процентов в году (m) | Срок кредита |
| 8,9 | 70 дней | 14,5 | 4 месяца | ||||
| 13,0 | 10 месяцев | 17,0 | 5 лет | ||||
| 11,5 | 2 года | 14,4 | 245 дней | ||||
| 7,2 | 3 года | 12,8 | 18 месяцев | ||||
| 10,7 | 1 год | 11,7 | 6 лет | ||||
| 12,9 | 120 дней | 13,9 | 7 месяцев | ||||
| 7,3 | 90 дней | 15,8 | 205 дней | ||||
| 9,8 | 15 месяцев | 13,1 | 5 лет | ||||
| 10,9 | 11 месяцев | 9,7 | 250 дней | ||||
| 14,5 | 4 года | 18,5 | 19 месяцев | ||||
| 9,3 | 7 лет | 8,3 | 8 лет | ||||
| 13,2 | 180 дней | 11,8 | 5 месяцев | ||||
| 21,2 | 6 месяцев | 7,9 | 110 дней | ||||
| 14,5 | 5 лет | 9,3 | 7 лет | ||||
| 10,4 | 200 дней | 14,7 | 330 дней |
Определите эквивалентную:
- сложную процентную ставку;
- простую процентную ставку;
- сложную учетную ставку;
- простую учетную ставку;
- номинальную процентную ставку.
3.11 Какая непрерывная ставка заменит: начисление процентов каждые два месяца; полугодовое; поквартальное начисление; ежемесячное начисление по номинальной ставке (таблица 3.9) годовых.
Таблица 3.9 – Величина номинальной процентной ставки
| Вариант | Процентная ставка, % | Вариант | Процентная ставка, % |
| 9,0 | 10,4 | ||
| 8,0 | 7,0 | ||
| 9,5 | 7,9 | ||
| 7,5 | 6,5 | ||
| 10,9 | 7,1 | ||
| 6,3 | 10,8 | ||
| 11,0 | 8,6 | ||
| 8,5 | 9,1 | ||
| 9,8 | 10,5 | ||
| 10,1 | 9,3 | ||
| 7,7 | 7,2 | ||
| 10,2 | 8,3 | ||
| 11,1 | 8,1 | ||
| 9,2 | 8,7 | ||
| 10,6 | 8,9 |
3.12 На определенную сумму денег в течение: 2 лет, 3 лет и 4 лет непрерывно начисляются проценты с силой роста (таблица 3.10). Определите эквивалентную номинальную процентную ставку, если проценты начислялись: по полугодиям, ежеквартально, ежемесячно, каждые два месяца.
Таблица 3.10 – Величина силы роста
| Вариант | Процентная ставка, % | Вариант | Процентная ставка, % |
| 8,0 | 8,8 | ||
| 9,0 | 9,1 | ||
| 7,5 | 10,5 | ||
| 9,5 | 12,5 | ||
| 10,9 | 11,4 | ||
| 11,3 | 14,8 | ||
| 10,0 | 11,6 | ||
| 8,9 | 12,1 | ||
| 9,8 | 11,9 |
Продолжение таблицы 3.10
| Вариант | Процентная ставка, % | Вариант | Процентная ставка, % |
| 10,7 | 10,8 | ||
| 10,1 | 11,2 | ||
| 13,2 | 12,3 | ||
| 11,1 | 7,7 | ||
| 11,5 | 11,7 | ||
| 10,6 | 12,6 |
3.13 На сумму денег в течение 6 лет непрерывно начисляются проценты с начальной силой роста 10,3 % и ежегодным абсолютным приростом в 2,0 %. Определите эквивалентную ставку сложных процентов.
3.14 Определите величину силы роста при начислении непрерывных процентов, эквивалентную учетной ставке в размере 16,7 % годовых, как простых так и сложных.
3.15 Клиент получил в банке три ссуды.
Таблица 3.11 – Условия получения ссуд по вариантам
| Вари- ант | Ссуда 1 | Ссуда 2 | Ссуда 3 | |||
| Срок | Ставка, % | Срок | Ставка, % | Срок | Ставка, % | |
| 10 дней | 11,5 | 15 дней | 12,3 | 20 дней | 13,5 | |
| 1 месяц | 10,8 | 2 месяца | 12,3 | 3 месяца | 14,7 | |
| 30 дней | 9,8 | 40 дней | 11,5 | 50 дней | 12,3 | |
| 60 дней | 10,0 | 75 дней | 11,0 | 80 дней | 11,8 | |
| 80 дней | 10,5 | 90 дней | 11,4 | 100 дней | 11,9 | |
| 1 год | 10,0 | 2 года | 12,0 | 3 года | 13,6 | |
| 4 года | 11,0 | 6 лет | 12,5 | 9 лет | 13,0 | |
| 3 месяца | 11,2 | 4 месяца | 11,9 | 7 месяцев | 12,3 | |
| 4 месяца | 11,3 | 5 месяцев | 11,8 | 6 месяцев | 12,2 | |
| 4 месяца | 11,4 | 7 месяцев | 12,8 | 9 месяцев | 13,2 | |
| 2 года | 11,2 | 3 года | 12,3 | 6 лет | 12,9 | |
| 90 дней | 11,9 | 120 дней | 12,8 | 150 дней | 13,2 | |
| 5 месяцев | 11,7 | 6 месяцев | 13,9 | 7 месяцев | 14,9 | |
| 3 месяца | 11,8 | 5 месяцев | 13,7 | 8 месяцев | 14,3 | |
| 110 дней | 10,8 | 140 дней | 12,9 | 160 дней | 14,5 | |
| 4 года | 12,3 | 7 лет | 14,8 | 8 лет | 16,7 | |
| 150 дней | 13,8 | 180 дней | 14,9 | 200 дней | 15,6 | |
| 2 месяца | 14,5 | 3 месяца | 15,9 | 6 месяцев | 16,8 | |
| 170 дней | 13,5 | 190 дней | 13,9 | 210 дней | 14,8 | |
| 3 месяца | 13,2 | 6 месяцев | 14,8 | 9 месяцев | 15,6 | |
| 2 года | 16,8 | 4 года | 17,7 | 6 лет | 18,2 | |
| 6 месяцев | 15,9 | 8 месяцев | 16,3 | 11 месяцев | 17,2 | |
| 180 дней | 12,8 | 220 дней | 14,3 | 240 дней | 15,2 | |
| 3 года | 12,4 | 5 лет | 13,5 | 10 лет | 14,1 |
Продолжение таблицы 3.11
| Вари- ант | Ссуда 1 | Ссуда 2 | Ссуда 3 | |||
| Срок | Ставка, % | Срок | Ставка, % | Срок | Ставка, % | |
| 6 месяцев | 13,2 | 9 месяцев | 14,8 | 12 месяцев | 16,5 | |
| 210 дней | 13,4 | 240 дней | 13,9 | 280 дней | 14,8 | |
| 1 год | 14,5 | 3 года | 15,8 | 4 года | 16,7 | |
| 4 месяца | 13,2 | 7 месяцев | 14,7 | 10 месяцев | 15,4 | |
| 250 дней | 12,5 | 300 дней | 13,8 | 330 дней | 14,7 | |
| 5 лет | 14,8 | 7 лет | 15,0 | 10 лет | 15,9 |
Определите среднюю:
- простую процентную ставку;
- сложную учетную ставку;
- сложную процентную ставку.
3.16 По условиям погашения кредита, полученного под 15,0 % (простые проценты) 10 марта, фирма должна выплатить суммы в 4 срока:
- 15 апреля – 280000 руб.;
- 15 июня – 250000 руб.;
- 30 августа – 240000 руб.;
- 28 сентября – 300000 руб.
В связи со сложившимися обстоятельствами фирма просит банк объединить эти платежи в один и перенести дату выплаты долга на 10 августа.
Определите величину консолидированного платежа.
Определите величину консолидированного платежа, если использовалась сложная учетная ставка в размере 14,5 %.
3.17 Клиент взял в банке три кредита. Платежи по этим кредитам клиент желает объединить в один. Найдите консолидированную сумму платежа, если использовалась:
а) простая процентная ставка в размере 11,0%;
б) простая учетная ставка в размере 12,5 %;
в) сложная процентная ставка в размере 13,0 %;
г) сложная учетная ставка в размере 13,5 %.
Задачу решите для двух согласованных сроков.
Таблица 3.12 – Условия консолидации кредитов
| Вари- ант | Кредит 1 | Кредит 2 | Кредит 3 | Согласованные сроки платежей | ||||
| Сумма, тыс. руб. (Р) | Срок кредита | Сумма, тыс. руб. (Р) | Срок кредита | Сумма, тыс. руб. (Р) | Срок кредита | первый | второй | |
| 10,0 | 40 дней | 20,0 | 60 дней | 30,0 | 70 дней | 80 дней | 65 дней | |
| 15,0 | 2 года | 20,0 | 4 года | 25,0 | 6 лет | 7 лет | 5 лет | |
| 30,0 | 60 дней | 35,0 | 70 дней | 40,0 | 100 дней | 120 дней | 90 дней | |
| 20,0 | 1 месяц | 30,0 | 3 месяца | 40,0 | 6 месяцев | 8 мес. | 5 мес. |
Продолжение таблицы 3.12
| Ва-ри- ант | Кредит 1 | Кредит 2 | Кредит 3 | Согласованные сроки платежей | ||||||
| Сумма, тыс. руб. (Р) | Срок кредита | Сумма, тыс. руб. (Р) | Срок кредита | Сумма, тыс. руб. (Р) | Срок кредита | первый | второй | |||
| 30,0 | 1 год | 40,0 | 3 года | 50,0 | 6 лет | 8 лет | 5 лет | |||
| 35,0 | 2 месяца | 40,0 | 4 месяца | 45,0 | 6 месяцев | 7 мес. | 5 мес. | |||
| 40,0 | 80 дней | 45,0 | 100 дней | 50,0 | 150 дней | 180 дней | 120 дней | |||
| 45,0 | 3 года | 50,0 | 5 лет | 55,0 | 7 лет | 9 лет | 6 лет | |||
| 50,0 | 3 месяца | 55,0 | 7 месяцев | 60,0 | 8 месяцев | 10 мес. | 5 мес. | |||
| 57,0 | 45 дней | 60,0 | 90 дней | 63,0 | 140 дней | 200 дней | 120 дней | |||
| 60,0 | 200 дней | 65,0 | 240 дней | 70,0 | 330 дней | 350 дней | 290 дней | |||
| 20,0 | 2 года | 40,0 | 5 лет | 60,0 | 6 лет | 8 лет | 4 года | |||
| 25,0 | 100 дней | 40,0 | 180 дней | 55,0 | 240 дней | 280 дней | 170 дней | |||
| 10,0 | 3 месяца | 25,0 | 6 месяцев | 35,0 | 9 месяцев | 11 мес. | 7 мес. | |||
| 30,0 | 4 года | 60,0 | 5 лет | 70,0 | 6 лет | 8 лет | 6 лет | |||
| 38,0 | 120 дней | 45,0 | 180 дней | 60,0 | 250 дней | 300 дней | 200 дней | |||
| 40,0 | 2 месяца | 58,0 | 3 месяца | 63,0 | 7 месяцев | 8 мес. | 5 мес. | |||
| 50,0 | 170 дней | 67,0 | 220 дней | 80,0 | 290 дней | 320 дней | 210 дней | |||
| 60,0 | 150 дней | 65,0 | 190 дней | 70,0 | 280 дней | 340 дней | 210 дней | |||
| 65,0 | 3 года | 73,0 | 5 лет | 78,0 | 7 лет | 9 лет | 6 лет | |||
| 65,0 | 140 дней | 75,0 | 190 дней | 85,0 | 270 дней | 300 дней | 240 дней | |||
| 60,0 | 4 месяца | 70,0 | 7 месяцев | 80,0 | 10 мес. | 11 мес. | 8 мес. | |||
| 70,0 | 80 дней | 78,0 | 120 дней | 83,0 | 190 дней | 220 дней | 150 дней | |||
| 70,0 | 4 года | 80,0 | 5 лет | 100,0 | 7 лет | 10 лет | 6 лет | |||
| 80,0 | 5 месяцев | 85,0 | 8 месяцев | 99,0 | 11 мес. | 14 мес. | 10 мес. | |||
| 79,0 | 95 дней | 90,0 | 130 дней | 103,0 | 200 дней | 230 дней | 180 дней | |||
| 22,0 | 6 месяцев | 45,0 | 10 мес. | 63,0 | 12 мес. | 15 мес. | 9 мес. | |||
| 95,0 | 160 дней | 104,0 | 250 дней | 110,0 | 340 дней | 350 дней | 290 дней | |||
| 30,0 | 2 года | 64,0 | 4 года | 80,0 | 6 лет | 8 лет | 5 лет | |||
| 37,0 | 4 месяца | 59,0 | 9 месяцев | 78,0 | 11 мес. | 12 мес. | 10 мес. | |||
3.18 Предприятие имеет ряд обязательств перед кредитором: 450000 руб., 689000 руб., 897000 руб., которые должны быть выплачены соответственно через 80, 100 и 130 дней после заключения контракта. По согласованию сторон было решено эти платежи заменить одним платежом равным 2300 тыс. руб. (S0) с продлением срока оплаты, используя:
а) простую процентную ставку 14,7 %;
б) сложную процентную ставку 12,5 %.
Определите:
а) срок погашения задолженности, если использовалась французская практика;
б) современную стоимость платежей.
Вопросы для самоконтроля
1. Какие процентные ставки называются эквивалентными?
2. Как производится усреднение процентных и учетных ставок?
3. Каким образом учитывается принцип финансовой эквивалентности обязательств?
4. Напишите уравнение эквивалентности размеров консолидированных платежей?
5. Составьте уравнение эквивалентности сроков консолидированного платежа?
| <== предыдущая страница | | | следующая страница ==> |
| Тема 2. СЛОЖНЫЕ ПРОЦЕНТЫ | | | Тема 4. ПОСТОЯННЫЕ ФИНАНСОВЫЕ РЕНТЫ |
Дата добавления: 2014-09-08; просмотров: 953; Нарушение авторских прав

Мы поможем в написании ваших работ!