
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тема 4. ПОСТОЯННЫЕ ФИНАНСОВЫЕ РЕНТЫ
Финансовая рента или аннуитет – это однонаправленный денежный поток с равными временными интервалами.
Финансовая рента характеризуется следующими параметрами:
R – величинагодового платежа;
n – срок ренты, лет;
i или j – годовые сложные процентные ставки, используемые для наращения ренты или дисконтирования платежей;
m – частота начисления процентов в году;
p – число рентных платежей в году;
S – наращенная сумма ренты, т.е. сумма всех платежей с начисленными на них процентами на конец срока ренты;
A – современная величина ренты (приведенная стоимость), т.е. сумма всех платежей, уменьшенная (дисконтированная) на величину процентной ставки на определенный момент времени (как правило, на начало ренты).
Таблица 4.1 – Определение наращенной суммы и современной стоимости
постоянной ренты постнумерандо
| Число платежей в году | Число начисления процентов в году | Наращенная сумма | Современная стоимость |
| p=1 | m=1 |  (4.1) (4.1)
| 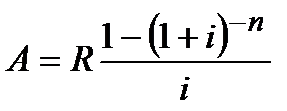 (4.2) (4.2)
|
| m>1 | 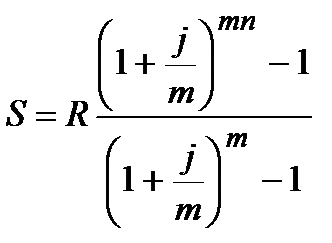 (4.3) (4.3)
| 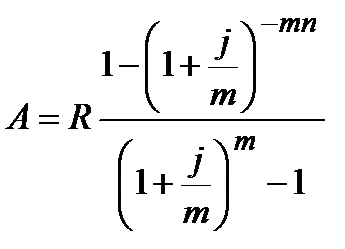 (4.4) (4.4)
| |
m 
| 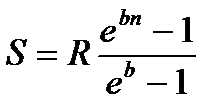 (4.5) (4.5)
| 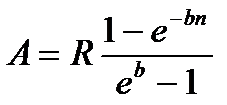 (4.6) (4.6)
| |
| Продолжение таблицы 4.1 | |||
| Число платежей в году | Число начисления процентов в году | Наращенная сумма | Современная стоимость |
| p>1 | m=1 | 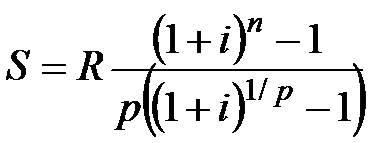 (4.7) (4.7)
| 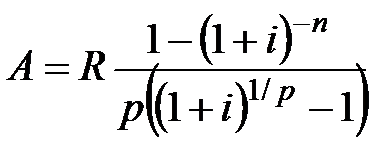 (4.8) (4.8)
|
| m=p | 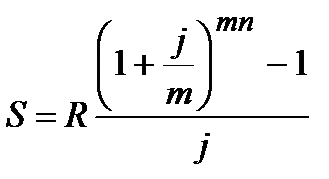 (4.9) (4.9)
|  (4.10) (4.10)
| |
| m¹p | 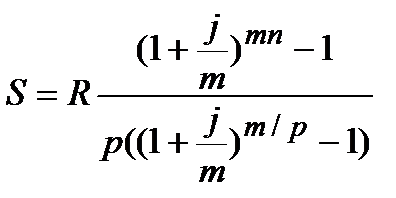 (4.11) (4.11)
| 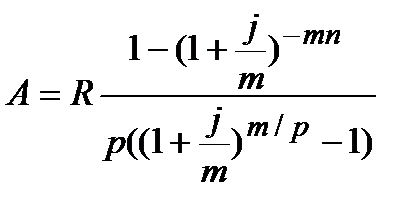 (4.12)
(4.12)
| |
m 
| 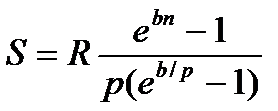 (4.13) (4.13)
|  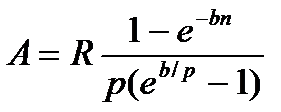 (4.14) (4.14)
|
При разработке контрактов и условий финансовых операций могут возникнуть случаи, когда задается одна из двух обобщающих характеристик – S или A, а необходимо рассчитать значение недостающего параметра.
Таблица 4.2 – Расчет величины годового платежа постоянных рент
постнумерандо
| Число платежей в году | Частота начисления процентов в году | Исходные параметры | |
| S | A | ||
| p=1 | m=1 | 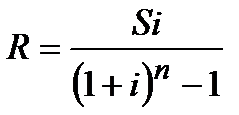 (4.15) (4.15)
| 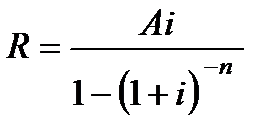 (4.16) (4.16)
|
| m>1 | 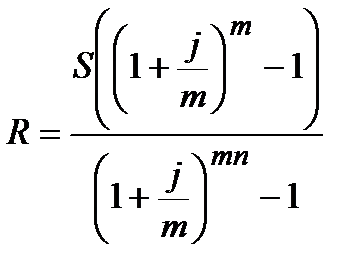 (4.17) (4.17)
|  (4.18) (4.18)
| |
m 
| 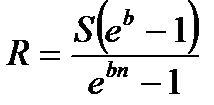 (4.19) (4.19)
| 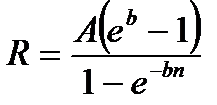 (4.20) (4.20)
| |
| Продолжение таблицы 4.2 | |||
| Число платежей в году | Частота начисления процентов в году | Исходные параметры | |
| S | A | ||
| p>1 | m=1 | 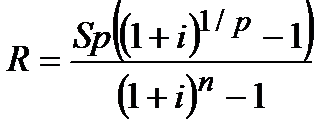 (4.21) (4.21)
| 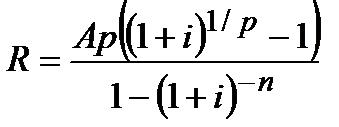 (4.22) (4.22)
|
| m=p | 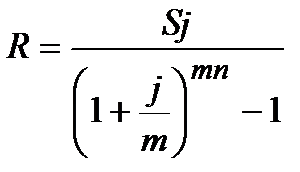 (4.23) (4.23)
| 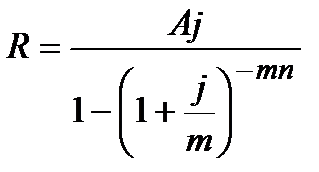 (4.24) (4.24)
| |
| m¹p | 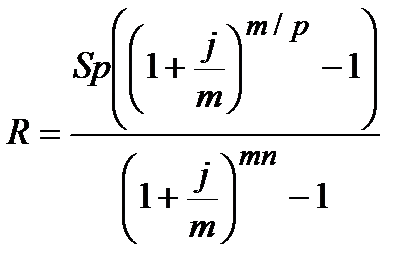 (4.25) (4.25)
|  (4.26)
(4.26)
| |
m 
| 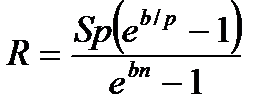 (4.27) (4.27)
| 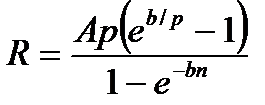 (4.28) (4.28)
|
В случае согласования остальных параметров финансовой сделки срок ренты можно рассчитать с помощью величины наращенной суммы или современной стоимости ренты.
Таблица 4.3 – Расчет срока постоянных рент постнумерандо
| Число платежей в году | Число начислений процентов в году | Исходные параметры | |
| S | A | ||
| p=1 | m=1 |  (4.29) (4.29)
| 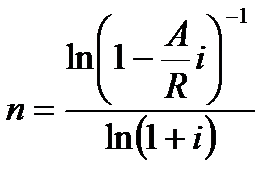 (4.30) (4.30)
|
| m>1 | 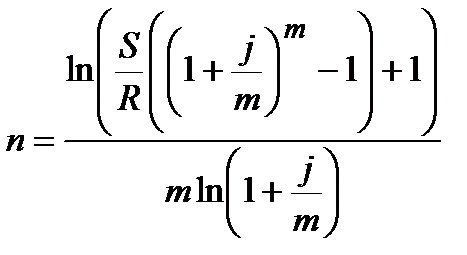 (4.31)
(4.31)
| 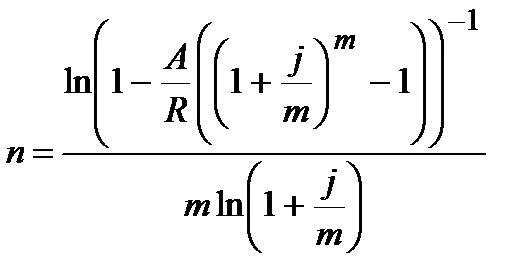 (4.32)
(4.32)
| |
m 
| 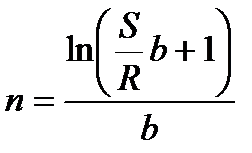 (4.33) (4.33)
| 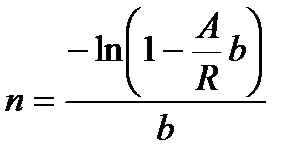 (4.34) (4.34)
| |
| Число платежей в году | Число начислений процентов в году | Исходные параметры | |
| S | A | ||
| p>1 | m=1 | 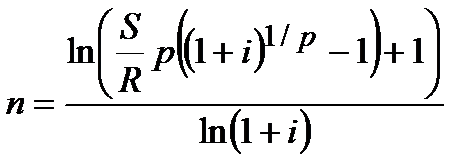 (4.35)
(4.35)
| 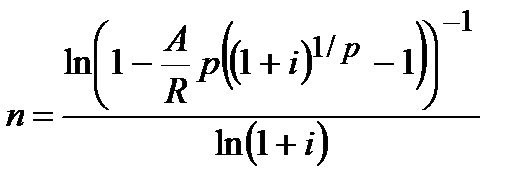 (4.36)
(4.36)
|
| m=p | 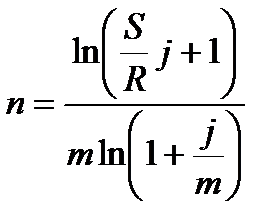 (4.37) (4.37)
| 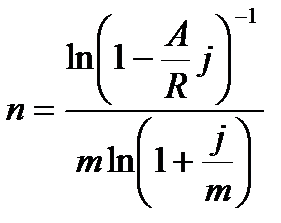 (4.38) (4.38)
| |
| m¹p | 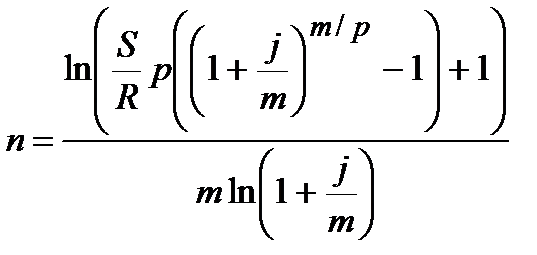 (4.39)
(4.39)
| 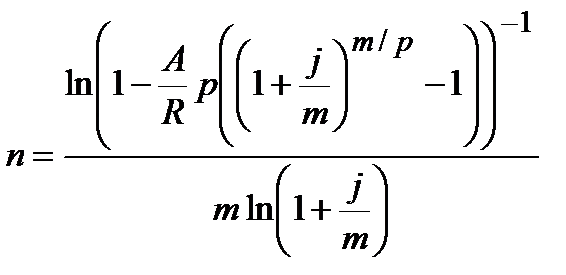 (4.40)
(4.40)
| |
m 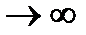
| 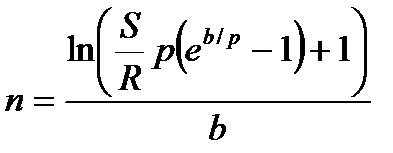 (4.41) (4.41)
| 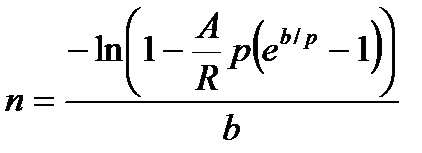 (4.42)
(4.42)
|
При расчете срока ренты нужно принять во внимание следующее:
а) расчетные значения срока будут, как правило, дробные, тогда для годовой ренты в качестве n удобно принять ближайшее целое число лет;
б) в связи с округлением величины n до целого значения необходимо пересчитать величину годового рентного платежа R с тем, чтобы наращенная сумма (или современная стоимость) ренты осталась неизменной.
Величину процентной ставки ренты определяют обычно методом линейной интерполяции следующим образом:
а) при известных величинах наращенной суммы ренты S, годового платежа R и коэффициента наращения ренты 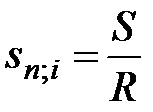
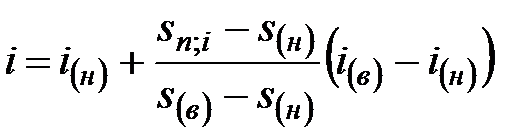 , (4.43)
, (4.43)
где 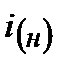 и
и 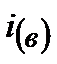 – нижнее и верхнее значения предполагаемой процентной ставки;
– нижнее и верхнее значения предполагаемой процентной ставки;
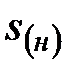 и
и 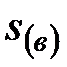 – нижнее и верхнее значения коэффициентов наращения
– нижнее и верхнее значения коэффициентов наращения
ренты для ставок 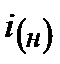 и
и  ;
;
б) при известных величинах современной стоимости ренты A, годового платежа R и коэффициента приведения ренты 
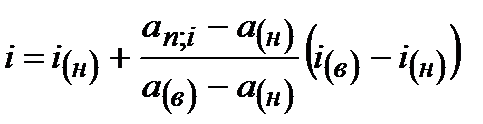 , (4.44)
, (4.44)
где  и
и  – значения коэффициентов приведения ренты для ставок
– значения коэффициентов приведения ренты для ставок 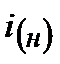 и
и  .
.
При расчетах рентных платежей в финансовой практике чаще всего используются сложные проценты. Однако существуют рентные платежи, в которых начисление производится по ставкам простых процентов, при этом наращенная сумма и современная стоимость ренты определяются по формулам:
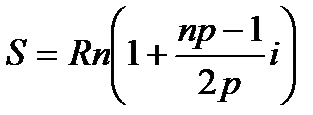 ; (4.45)
; (4.45)
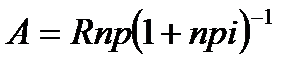 , (4.46)
, (4.46)
где p – число рентных платежей в году.
Таблица 4.4 – Определение наращенной суммы и современной стоимости
ренты пренумерандо
| Число платежей в году | Частота начислений процентов в году | Наращенная сумма | Современная стоимость |
| p=1 | m=1 | 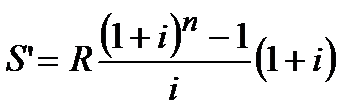 (4.47) (4.47)
| 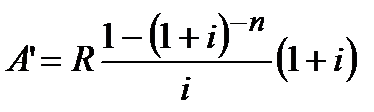 (4.48) (4.48)
|
| m>1 | 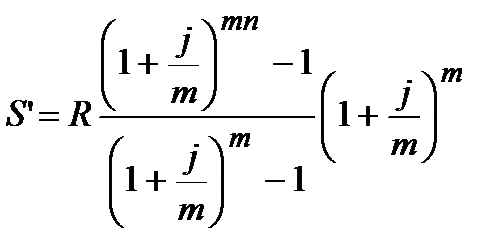 (4.49)
(4.49)
| 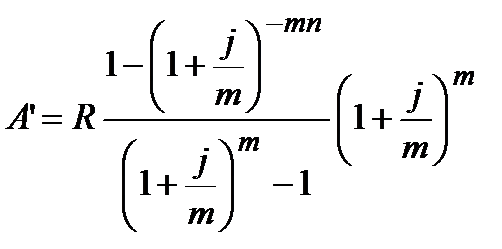 (4.50)
(4.50)
| |
m 
| 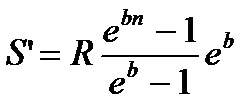 (4.51) (4.51)
|
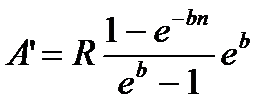 (4.52) (4.52)
| |
| Число платежей в году | Частота начислений процентов в году | Наращенная сумма | Современная стоимость |
| p>1 | m=1 | 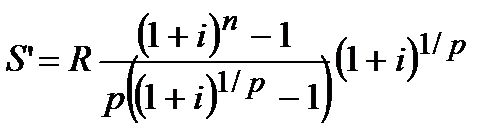 (4.53)
(4.53)
| 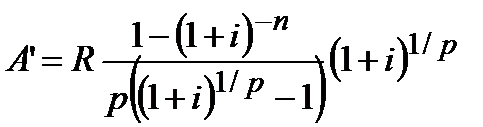 (4.54)
(4.54)
|
| m=p | 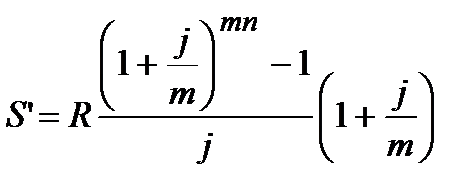 (4.55) (4.55)
| 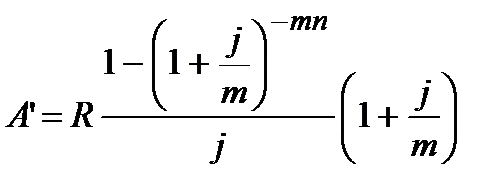 (4.56) (4.56)
| |
| m¹p | 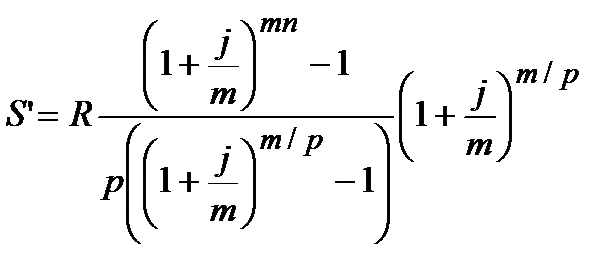 (4.57)
(4.57)
| 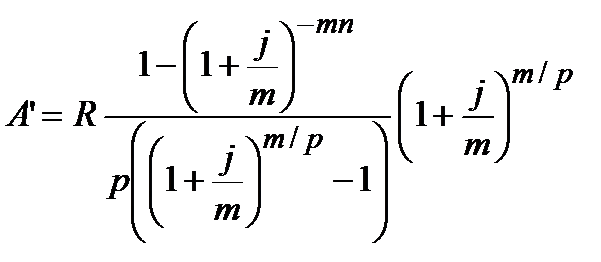 (4.58)
(4.58)
| |
m 
| 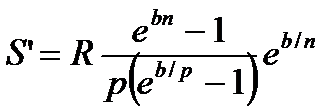 (4.59) (4.59)
| 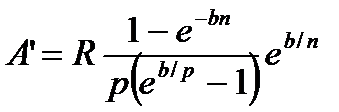 (4.60) (4.60)
|
Пример 4.1 Фирма создает инвестиционный фонд. В течение 5 лет в фонд вносятся платежи в размере 75000 руб. в год под 12% годовых. Найти величину инвестиционного фонда через 5 лет, если: 1) платежи осуществляются один раз в году, проценты начисляются один раз в году; 2) платежи осуществляются один раз в году, проценты начисляются ежеквартально; 3) платежи осуществляются по полугодиям, проценты начисляются один раз в году; 4) платежи осуществляются по полугодиям, проценты начисляются по полугодиям; 5) платежи осуществляются по полугодиям, проценты начисляются ежеквартально.
Решение. По формулам (4.1), (4.3), (4.7), (4.9), (4.11) находим величину наращенной суммы ренты постнумерандо.
1) p=1, m=1, 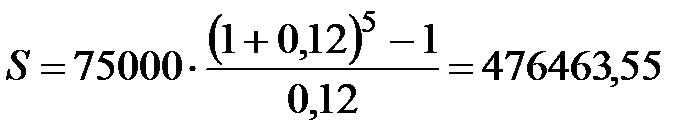 руб.;
руб.;
2)p=1, m=4,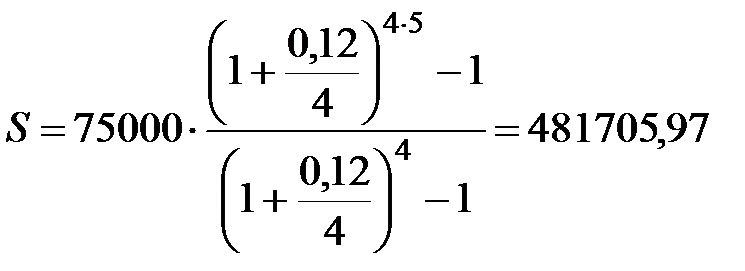 руб.;
руб.;
3) p=2, m=1,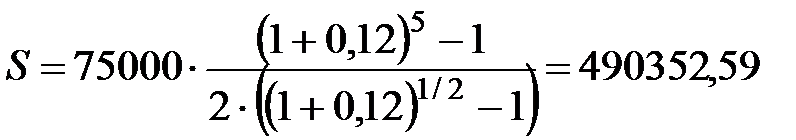 руб.;
руб.;
4) p=2, m=2,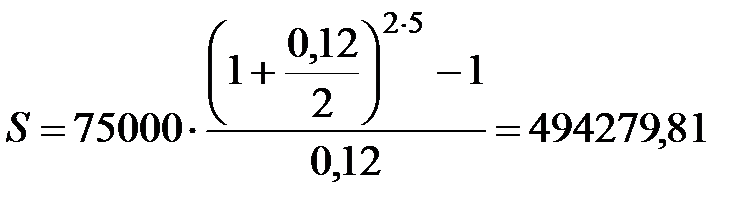 руб.;
руб.;
5) p=2, m=4,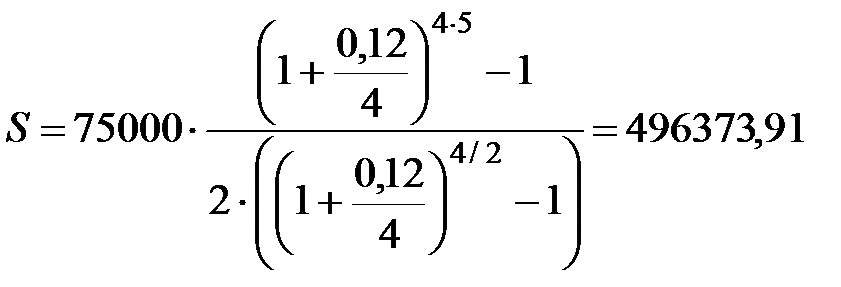 руб.
руб.
Пример 4.2 Фирма предусматривает создание в течение 4-х лет фонда развития и имеет возможность вносить ежегодно 34700 руб. под 8% годовых. Какая сумма потребовалась бы фирме изначально для создания фонда, если бы она поместила ее в банк на 4 года под 8% годовых, если: 1) платежи осуществляются один раз в году, проценты начисляются один раз в году; 2) платежи осуществляются один раз в году, проценты начисляются ежеквартально; 3) платежи осуществляются по полугодиям, проценты начисляются один раз в году; 4) платежи осуществляются по полугодиям, проценты начисляются по полугодиям; 5) платежи осуществляются по полугодиям, проценты начисляются ежеквартально.
Решение. Найдем современную величину ренты постнумерандо, используя формулы (4.2), (4.4), (4.8), (4.10), (4.12).
1) p=1, m=1, 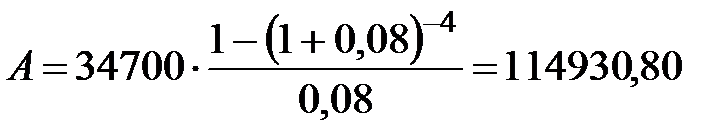 руб.;
руб.;
2) p=1, m=4, 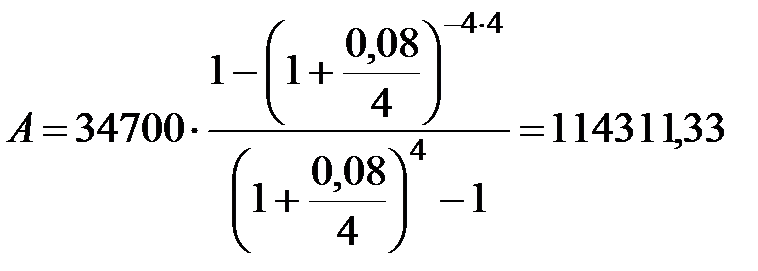 руб.;
руб.; 
3) p=2, m=1, 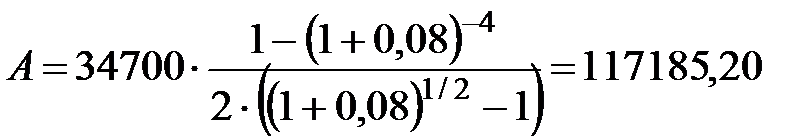 руб.;
руб.;
4) p=2, m=2, 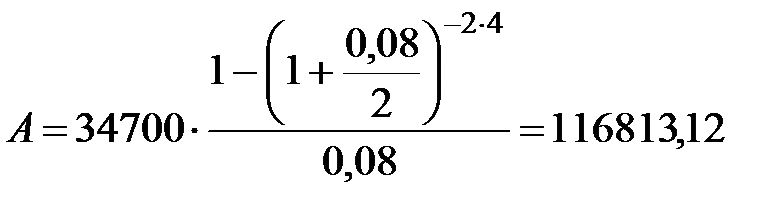 руб.;
руб.;
5) p=2, m=4, 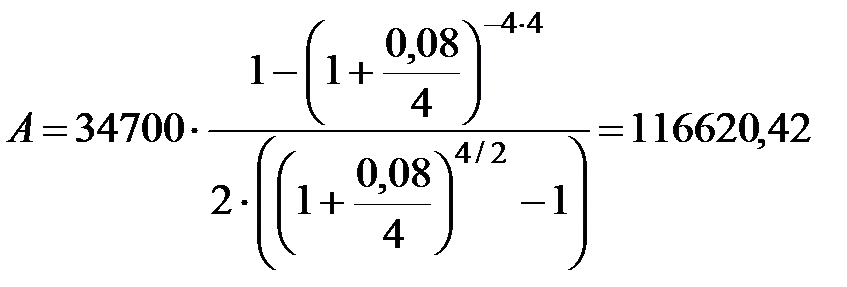 руб.
руб.
Пример 4.3 Какой срок необходим для накопления 400 тыс. руб., если ежеквартально будет вноситься 10 тыс. руб. под 12 % годовых при ежегодном начислении процентов?
Решение. Так как величина наращенной суммы S=400 тыс. руб., число начислений процентов в году m = 1, рентные платежи вносятся ежеквартально (p=4), а R-величина годового взноса составляет 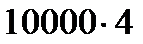 =40 000 руб. то по формуле (4.35)
=40 000 руб. то по формуле (4.35)
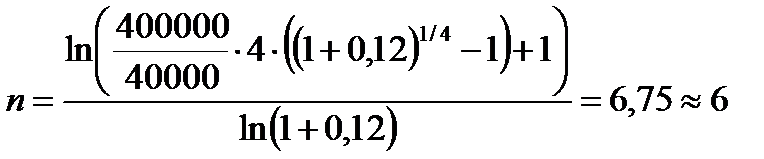 лет.
лет.
Вследствие округления срока ренты необходимо пересчитать величину годового взноса по формуле (4.21)
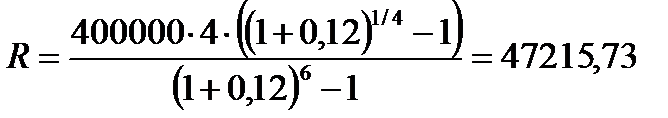 руб.,
руб.,
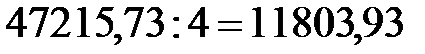 .
.
Таким образом, ежеквартально необходимо вносить 11803,93 руб.
Задачи для самостоятельного решения
4.1 Страховая компания заключила договор с предприятием на: 2 года, 3 года, 4 года, 7 лет, установив годовой страховой взнос в сумме (таблица 4.5). Страховые взносы помещаются в банк под сложную процентную ставку 12% годовых. Определите сумму, которую получит страховая компания по этому контракту, если взносы будут поступать: а) в конце каждого года при ежегодном начислении процентов; б) в конце каждого года при полугодовом начислении процентов; в) равными долями в конце каждого полугодия при ежегодном начислении процентов; г) равными долями в конце каждого квартала при ежеквартальном начислении процентов; д) равными долями в конце каждого квартала при ежемесячном начислении процентов.
Таблица 4.5 – Величина годового взноса
| Вариант | Сумма, тыс. руб. | Вариант | Сумма, тыс. руб. |
Продолжение таблицы 4.5
| Вариант | Сумма, тыс. руб. | Вариант | Сумма, тыс. руб. |
4.2. Определите современную стоимость всех платежей по всем вариантам задачи 4.1.
4.3. Для создания фонда фирма вкладывает ежегодно в банк по 124 тыс. руб. под годовую номинальную процентную ставку 12%. Определите сумму, которая будет накоплена в фонде через 8 лет, если: а) взносы делаются в конце года, а сложные проценты начисляются по полугодиям; б) взносы делаются равными долями в конце каждого месяца, а сложные проценты начисляются ежеквартально; в) взносы делаются равными долями в конце каждого квартала и начисляются непрерывные проценты.
4.4. Страховая компания, заключив на 4 года договор с некоторой фирмой, получает от нее страховые взносы по 150 тыс. руб. в конце каждого квартала. Эти взносы компания помещает в банк под годовую номинальную процентную ставку 11% годовых. Найдите приведенную стоимость суммы, которую получит страховая компания по данному контракту, если сложные проценты начисляются: а) ежеквартально; б) ежемесячно; в) непрерывно.
4.5. Клиент хочет накопить на своем счете сумму (таблица 4.6), осуществляя в конце каждого года равные вклады в банк под сложную процентную ставку 10% годовых. Какой величины должен быть каждый вклад, чтобы клиент мог накопить требуемую сумму за: а) 3 года; б) 5 лет; в) 7 лет; г) 10 лет?
Таблица 4.6 – Величина фонда
| Вариант | Сумма, тыс. руб. | Вариант | Сумма, тыс. руб. |
4.6. Предприниматель, с целью покупки оборудования, делает в конце каждого квартала равные вклады в банк под годовую номинальную процентную ставку 14%, причем сложные проценты начисляются по полугодиям. Какой величины должен быть каждый вклад, чтобы предприниматель мог накопить 1000 тыс. руб. за: а) 3 года; б) 5 лет; в) 8 лет.
4.7. Предприятие намеревается создать за 5 лет фонд развития в размере (таблица 4.7). Какую сумму предприятие должно ежегодно ассигновать на эту цель при условии помещения денег в банк в конце каждого года под процентную ставку 14% годовых с начислением сложных процентов: а) ежегодно; б) по полугодиям; в) ежеквартально; б) ежемесячно; д) непрерывно?
Таблица 4.7 – Величина фонда
| Вариант | Сумма, тыс. руб. | Вариант | Сумма, тыс. руб. |
4.8. Для создания за 5 лет фонда в размере 1 млн. руб. фирма делает ежегодные равные взносы в банк под годовую номинальную процентную ставку 11%. Определите, какой величины взнос должна ежегодно делать фирма, если: а) взносы делаются в конце года, а сложные проценты начисляются ежемесячно; б) взносы делаются равными долями в конце каждого полугодия, а сложные проценты начисляются ежеквартально; в) взносы делаются равными долями в конце каждого квартала и начисляются непрерывные проценты.
4.9. Анализируются два варианта накопления средств по схеме аннуитета пренумерандо: а) вносить на депозит сумму в размере 15 тыс. руб. каждый квартал при условии, что банк начисляет 10% годовых с ежеквартальным начислением сложных процентов; б) делать ежегодный вклад в размере 52 тыс. руб. на условиях 12% годовых при ежегодном начислении сложных процентов. Какая сумма будет на счете через 8 лет при реализации каждого плана? Какой план более предпочтителен? Изменится ли Ваш выбор, если процентная ставка во втором плане будет увеличена до 13%?
4.10. Клиент хочет накопить на своем счете 800 тыс. руб., осуществляя в конце каждого года равные вклады в банк в размере 150 тыс. руб. под сложную процентную ставку 13% годовых. За какой срок он сможет это сделать? Как изменится ответ задачи, если проценты будут начисляться: по полугодиям; ежеквартально; ежемесячно?
4.11. Определите срок, необходимый для создания инвестиционного фонда в размере 10 млн. руб., если планируется а) вносить по полугодиям 100 тыс. руб. под 12% годовых; б) ежемесячно осуществлять взносы в размере 15 тыс. руб. под 14% годовых с ежеквартальным начислением процентов.
4.12. Путем ежегодных взносов постнумерандо по 300 тыс. руб. предполагается за 3 года накопить 1200 тыс. руб. Какова должна быть годовая процентная ставка?
4.13. Клиент в конце каждого года вкладывает 14 тыс. руб. в банк, выплачивающий простые проценты по ставке 10% годовых. Определите сумму, которая будет на счете клиента через 3 года. Как изменится ответ задачи, если деньги вносятся по полугодиям по 7 тыс. руб.?
Вопросы для самоконтроля
1. Какой денежный поток называется потоком постнумерандо?
2. Какой денежный поток называется потоком пренумерандо?
3. В рамках решения каких двух задач может выполняться оценка денежного потока?
4. Какой денежный поток называют аннуитетом?
5. Что называется членом аннуитета, периодом аннуитета?
6. Какой аннуитет называется срочным?
7. Какой аннуитет называется p-срочным?
8. Какой аннуитет называется постоянным?
9. Что такое наращенная сумма ренты?
10. Что такое приведенная стоимость ренты?
11. Что называется коэффициентом наращения и приведения ренты?
12. Какие проценты в основном используются при оценке ренты?
13. Какой аннуитет называется отсроченным?
14. Что такое вечная рента?
| <== предыдущая страница | | | следующая страница ==> |
| КОНСОЛИДАЦИЯ ПЛАТЕЖЕЙ | | | КОНВЕРСИЯ ФИНАНСОВЫХ РЕНТ |
Дата добавления: 2014-09-08; просмотров: 1085; Нарушение авторских прав

Мы поможем в написании ваших работ!