КОНВЕРСИЯ ФИНАНСОВЫХ РЕНТ

В практике встречаются случаи, когда члены потока платежей изменяются в течение срока ренты. Изменения могут быть связаны с какими-либо обстоятельствами объективного порядка, а иногда и случайными факторами.

Поток последовательных платежей, члены которого не являются постоянными величинами, называется переменной рентой. Изменение величины платежей может быть описано каким-либо законом или носить нерегулярный характер. При этом определяются параметры следующих видов рент:

а) ренты с разовыми изменениями платежей:

Наращенная сумма годовой ренты

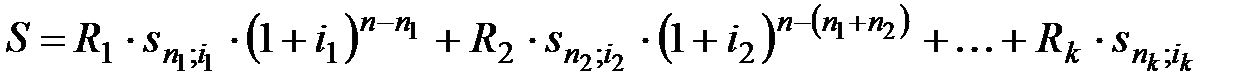, (5.1)

где 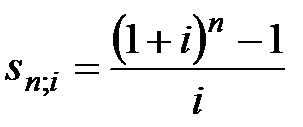– коэффициент наращения годовой ренты.

Современная величина годовой ренты

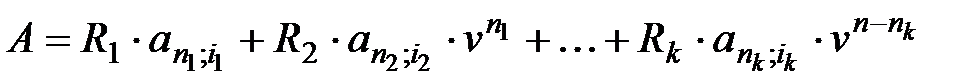, (5.2)

где 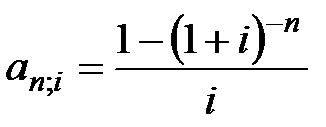– коэффициент приведения годовой ренты;

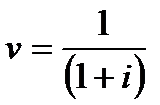– дисконтный множитель по ставке i;

n – срок ренты, n = n₁ + n₂ +…+ n_к;

n₁, n₂, …, n_к – продолжительность временных отрезков;

R₁, R₂, …, R_к - годовой платеж в соответствующем временном отрезке;

i₁, i₂, …, i_к – процентные ставки.

Если платежи вносятся несколько раз в году, то коэффициенты наращения ( 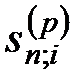) или приведения ( 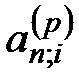) рассчитываются как для p-срочной ренты.

б) ренты с постоянным абсолютным изменением ее членов:

Наращенная сумма переменной ренты с постоянным абсолютным изменением ее членов составит:

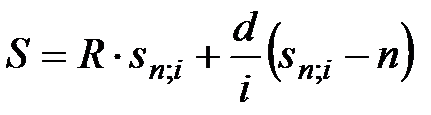, (5.3)

где d – разность арифметической прогрессии (величина абсолютного годового изменения членов ренты с соответствующим знаком),

R – первый член ренты.

Современная величина данной ренты составит:

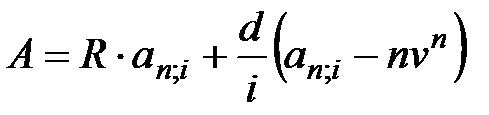. (5.4)

Зная значение постоянного прироста d, процентной ставки i, наращенной суммы S или текущей суммы долга A, определяется размер первого платежа R:

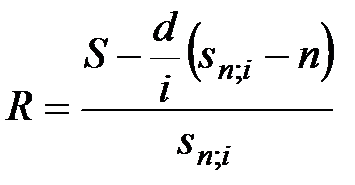; (5.5)

. (5.6)

Величина абсолютного прироста d определяется по формулам:

;

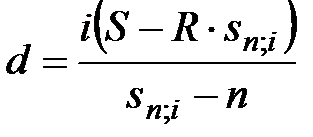(5.7)

.

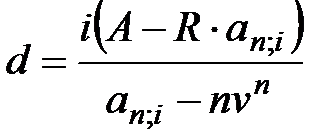Для переменной p-срочной ренты с постоянным абсолютным приростом платежей наращенная сумма и современная стоимость определяются по формулам:

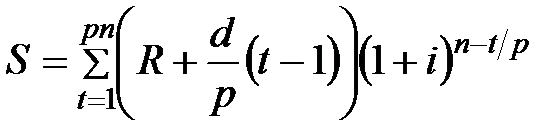; (5.8)

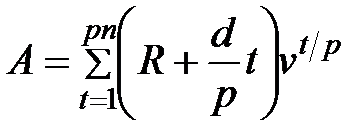. (5.9)

в) ренты с постоянным относительным приростом платежей:

Наращенная сумма и современная стоимость ренты составят:

а) при ежегодных платежах

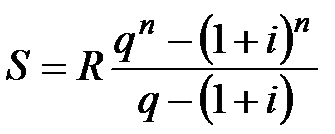; (5.10)

, (5.11)

где q – знаменатель прогрессии, т.е. коэффициент роста;

б) при p-срочной ренте

; (5.12)

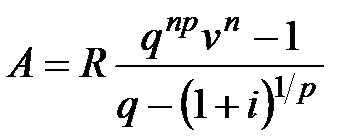. (5.13)

Расчеты по коммерческим сделкам могут предусматривать изменение условий оплаты, которое называется конверсией финансовых рент. Простейшими случаями конверсии являются выкуп ренты (замена ренты разовым платежом) и рассрочка платежа (замена разового платежа рентой).

Замена нескольких рент одной, параметры которой надо определить,называется консолидацией рент. Современная величина вновь образованной консолидированной ренты должна быть равна сумме современных величин консолидируемых рент:

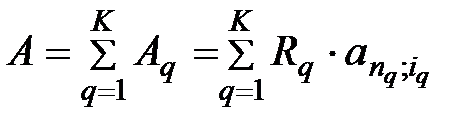, (5.14)

где А – современная величина консолидированной ренты;

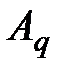– современная величина q-ой заменяемой ренты, q=1, 2, …, K;

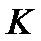– число консолидируемых рент;

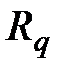– член q-ой ренты;

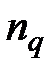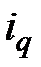и – соответственно продолжительность и процентная ставка q-ой ренты.

Членконсолидированной немедленной ренты определяется по формуле:

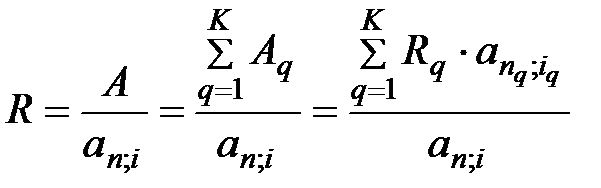, (5.15)

где 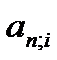– коэффициент приведения консолидированной ренты.

Членконсолидированной отсроченнойренты определяется по формуле:

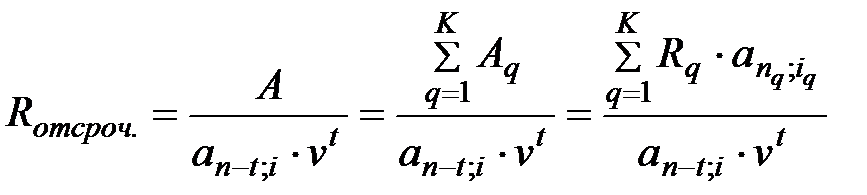, (5.16)

где 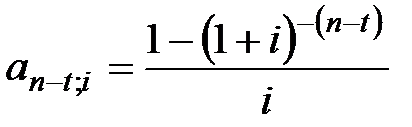– коэффициент приведения отсроченной консолидированной ренты;

t – продолжительность отсрочки, лет;

– процентная ставка консолидированной ренты;

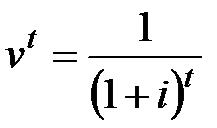– дисконтный множитель за период t, на который отложена рента.

Срок консолидированной немедленной ренты определяется по формуле:

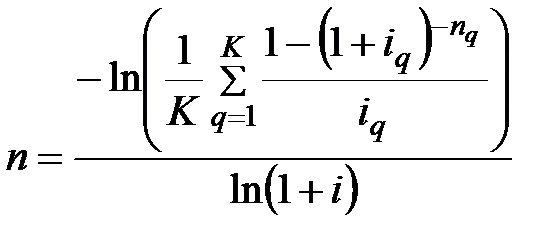. (5.17)

Если процентные ставки объединяемых рент и вновь создаваемой равны между собой, т.е. 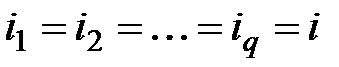, то

. (5.18)

Замена немедленной ренты на отсроченную, т.е. когда первый платеж по ренте переносится на более поздний срок в t лет. При этом возможны следующие варианты конверсии:

1) общая продолжительность ренты остается прежней, т.е. n₁ = n₂ = n, рентный платеж составит:

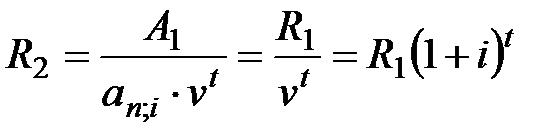, (5.19)

где 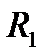и 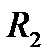– годовые платежи соответственно первоначальной и отсроченной ренты;

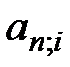– коэффициент приведения первоначальной годовой ренты;

t - продолжительность отсрочки;

2) общая продолжительность ренты изменяется, т.е. 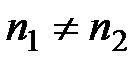, рентный платеж определяется по формуле:

, (5.20)

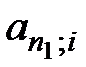где и 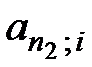– коэффициенты приведения соответственно первоначальной и отложенной рент;

3) члены ренты остаются неизменными, т.е. , тогда срок отложенной ренты составит:

.

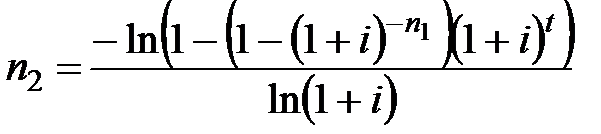Замена годовой ренты на p-срочную. Годовая немедленная рента с параметрами 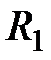, 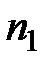заменяется на p-срочную с параметрами 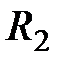, , 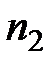p. Если заданы срок заменяющей ренты, ее периодичность и ставка, то

, (5.21)

где 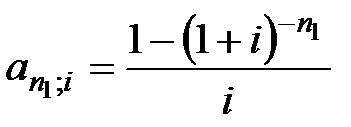– коэффициент приведения годовой ренты;

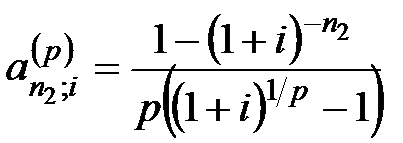– коэффициент приведения p-срочной ренты.

Если 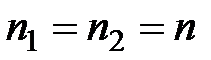, то

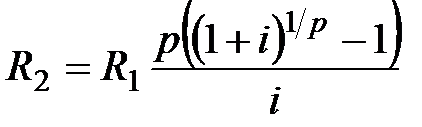. (5.22)

При изменении продолжительности ренты размер нового рентного платежа составит

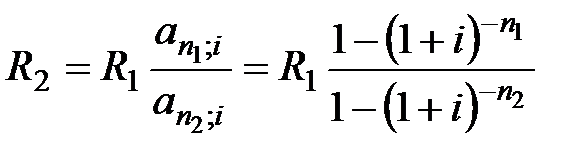. (5.23)

При изменении срочности ренты (числа выплат в году) годовой рентный платеж определяется по формуле:

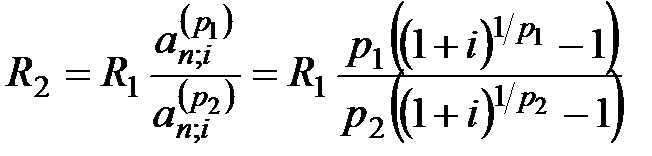, (5.24)

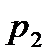где и – характеристики срочности двух рент.

Пример 5.1 По условиям контракта платежи вносятся в конце года, первый платеж составляет 2 млн. руб., каждый год его величина возрастает на 200 тыс. руб., срок выплат 4 года, процентная ставка 8%. Определить наращенную сумму.

Решение. Параметры ренты:

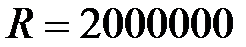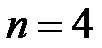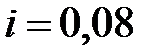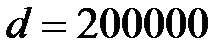руб.; 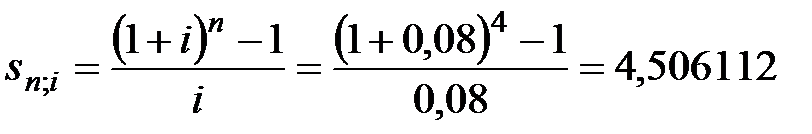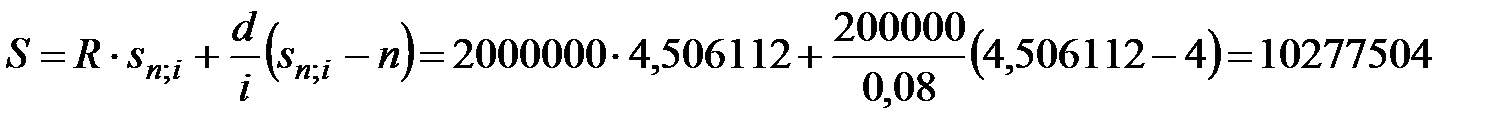; ; руб.;

.

руб.

Пример 5.2 Клиентом получен кредит сроком на 7 лет, при следующих условиях погашения: первый платеж 2 млн. руб., каждый следующий возрастает на 10%, платежи вносятся два раза в году, процентная ставка 8% годовых. Определить размер полученного кредита и сумму долга, подлежащую возврату.

Решение. Параметры ренты:

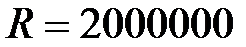руб.; ; ; ; .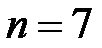

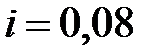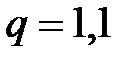Размер полученного кредита – это современная стоимость ренты.

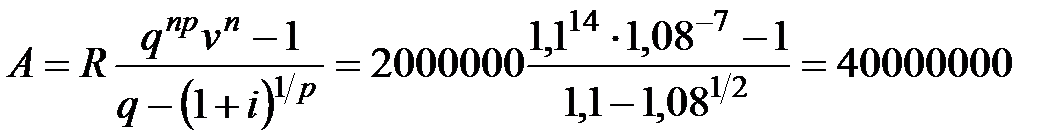руб.

руб.

Задачи для самостоятельного решения

5.1 Предприятием был получен кредит на 10 лет. Условия погашения кредита следующие: в первые пять лет платежи размером 6 млн. руб. вносятся каждый год под 11% годовых; следующие три года платежи размером 4 млн. руб. вносятся по полугодиям под 9% годовых. Последние два года ежеквартально вносятся платежи размером 3 млн. руб. под 8% годовых. Определите наращенную сумму долга по кредиту. Рассчитайте современную стоимость кредита.

5.2 Согласно условиям финансового соглашения на счет в банке в течение 7 лет: а) в конце года будут поступать денежные суммы, первая из которых равна 60 тыс. руб., а каждая следующая будет увеличиваться на 3000 руб.; б) каждое полугодие будут поступать платежи, первый из которых составит 35 тыс. руб., а каждый последующий будет увеличиваться на 1700 руб. Определите наращенную стоимость и приведенную величину этого аннуитета, если банк применяет процентную ставку 12% годовых, а сложные проценты начисляются один раз в кон­це года.

5.3 По условиям контракта на счет клиента в банке поступают в течение 6 лет в конце года платежи. Первый платеж равен 150 тыс. руб., а каждый следующий по отношению к предыдущему уве­личивается на 11%. Оцените этот аннуитет, если банк начисляет в конце каждого года сложные проценты из расчета 10% годо­вых.

5.4 За 5 лет необходимо накопить 1000 тыс. руб. Какой ве­личины должен быть первый вклад, если предполагается каж­дый год увеличивать величину денежного поступления на 15%, а процентная ставка равна 11% годовых? Денежные поступления и начисление сложных процентов осуществляются в конце года. Как изменится величина первого вклада, если предполагается ежеквартальный рост поступлений на 6%?

5.5 За 10 лет необходимо накопить 5000 тыс. руб. Какой ве­личины должен быть первый вклад, если предполагается каж­дый год увеличивать величину денежного поступления на 10000 руб., а процентная ставка равна 10% годовых? Денежные поступления и начисление сложных процентов осуществляются в конце года. Определите, на какую величину необходимо уве­личивать каждый год денежное поступление, если первый вклад будет равен 150 тыс. руб.

5.6 Три немедленные годовые ренты постнумерандо, с характеристиками: 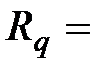130; 220 и 300 тыс. руб.; 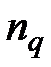= 5; 12 и 8 лет; 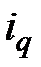= 14; 22 и 18% ; заменяются: а) одной немедленной рентой постнумерандо со сроком 10 лет и процентной ставкой 20% годовых; б) одной отсроченной на 3 года рентой с общим сроком 10 лет, включая отсрочку, и процентной ставкой 20% годовых. Определите величину годового платежа консолидированной ренты.

5.7. Объединяются три ренты со сроками 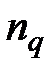= 7; 4 и 9 лет, члены рент равны между собой, а 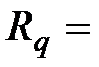500 тыс. руб.; процентные ставки также равны и составляют 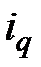= 8%. Размер консолидированного годового платежа равен 1,5 млн. руб., процентная ставка сохраняется на уровне 8% годовых. Определите срок новой ренты.

5.8. Фирма по торговле недвижимостью продает объект стоимостью 3,5 млн. руб. При этом предлагаются следующие варианты оплаты: а) оплата в течение трех лет равными платежами, вносимыми в конце года под 9% годовых; б) оплата с отсрочкой платежа в один год, остальные условия аналогичны предыдущему варианту; в) оплата с отсрочкой в один год, но срок ренты возрастает до четырех лет. Определите финансовые последствия для каждого варианта.

5.9. По условиям договора немедленная годовая рента сроком четыре года, величиной годового платежа 200 тыс. руб. и процентной ставкой 10 % годовых, заменяется отсроченной на два года рентой. Определите срок новой ренты при сохранении остальных параметров.

5.10. По условиям соглашения между кредитором и заемщиком годовая рента постнумерандо с величиной годового платежа 180 тыс. руб., сроком три года и ставкой 14% годовых, заменяется на квартальную при сохранении остальных параметров. Оцените новый аннуитет. Как изменятся параметры аннуитета, если срок ренты увеличится до четырех лет?

Вопросы для самоконтроля

1. Какой аннуитет называется переменным?

2. Приведите пример переменного аннуитета с постоянным аб­солютным изменением его членов. Какую последовательность обра­зуют члены такого аннуитета?

3. Приведите пример переменного аннуитета с постоянным относительным изменением его членов. Какую последовательность обра­зуют члены такого аннуитета?

4. Перечислите виды конверсии ренты.

5. Что такое консолидация ренты?

6. Что такое отсроченная рента?

Дата добавления: 2014-09-08; просмотров: 1261; Нарушение авторских прав

Мы поможем в написании ваших работ!