
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ТЕМА 1. ГАЗ, КАК РАБОЧЕЕ ТЕЛО ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
1.1. Структура основных понятий термодинамики авиационных ГТД
|
|
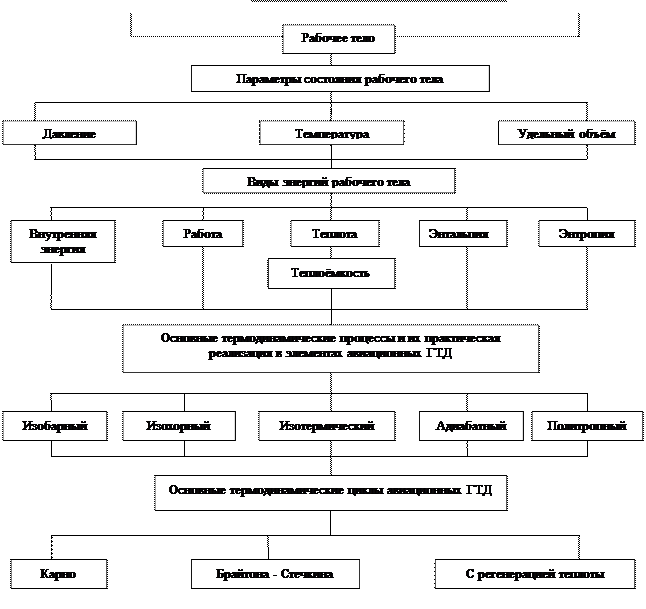 Рис. 1.1. Структура основных понятий термодинамики авиационных ГТД
Рис. 1.1. Структура основных понятий термодинамики авиационных ГТД
Применительно к авиационному двигателю рабочим телом называют воздух из атмосферы Земли, представляющий собой смесь газов (табл. 1.1.), его контрольной поверхностью является внутренняя поверхность цилиндра и поверхность поршня (в поршневых двигателях внутреннего сгорания), поверхность вращающихся и неподвижных лопаток и внутренняя поверхность каналов (в авиационных ГТД). В качестве внешней среды в авиационных двигателях выступает конструкция тепловой машины, форсунка, распыливающая топливо и другие элементы.
Таблица 1.1.
Состав сухого воздуха до высоты 90 км [15]
| Наименование составляющей атмосферного воздуха | Химическая формула | Масса одного киломоля кг/кмоль | Содержание составляющей в процентах |
| Азот Кислород Аргон Углекислый газ Неон Метан Сернистый ангидрид Гелий Криптон Водород Окись азота Ксенон Озон Перекись азота Йод | N2 O2 Ar CO2 Ne CH4 SO2 He Kr H2 N2O Xe O3 NO2 J2 | 28,0134 31,9968 39,9440 44,0079 20,1830 16,0000 64,0658 4,0026 83,8000 2,0159 1,0000 131,8000 48,0000 46,0000 126,9044 | 78,084 20,9476 0,934 0,0314 1,818·10-3 0,2·10-3 0,1·10-3 524·10-6 114·10-6 50·10-6 50·10-6 8,7·10-6 7·10-6 (летом) 2·10-6 (зимой) 2·10-6 1·10-6 |
1.2. Основные понятия и определения термодинамики
Каждая наука имеет свой объект изучения. Объектом исследования в термодинамике является различные термодинамические системы (ТДС), представляющие совокупность макроскопических тел, находящихся в тепловом и механическом взаимодействии как друг с другом, так и с внешней средой.
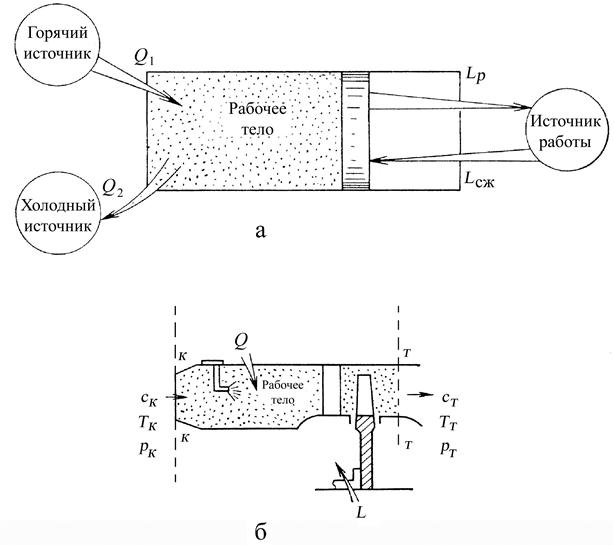
Рис. 1.2. Термодинамические системы:
а – закрытая, б – открытая
Внешней (окружающей) средой называют материальные тела, находящиеся за пределами термодинамической системы (рабочего тела). Границы раздела рабочего тела и внешней среды называют контрольной поверхностью или оболочкой.
Для обеспечения взаимного преобразования тепловой и механической энергии ТДС должна состоять из одного или нескольких источников теплоты, рабочего тела и источника работы. Схема ТДС представлена на рис. 1.2. Охарактеризуем кратко каждый элемент ТДС.
Источники теплоты обмениваются тепловой энергией с рабочим телом, Различают горячие и холодные источники теплоты. Горячим источником (теплоотдатчиком) является тело, сообщающее теплоту рабочему телу. Холодным источником (теплоприемником) является тело, принимающее от рабочего тела теплоту. Например, в ГТД горячим источником является факел пламени в камере сгорания, а холодным источником – атмосферный воздух, окружающий двигатель.
Источник работы обменивается механической энергией с рабочим телом. В ГТД источником работы является его ротор.
Преобразование теплоты в работу и наоборот осуществляется посредством рабочего тела. В ГТД рабочим телом является воздух, газ или другое вещество в газообразном состоянии, дающее наибольший эффект при преобразовании теплоты в работу. Это связано с тем, что газообразное вещество при нагревании способно увеличивать свой объём в большей степени, чем жидкость или твёрдое тело, и при этом совершать большую работу расширения. Такая способность газов обусловлена малостью сил взаимодействия между молекулами, поэтому при решении термодинамических задач этими силами вообще пренебрегают. Кроме того, считают, что молекулы имеют массу, но не имеют объёма. Такой газ называют идеальным. Реальный газ можно рассматривать как идеальный, если он находится в достаточно разреженном состоянии. Так, при течении через тепловой двигатель газ имеет относительно низкую плотность, поэтому можно считать его идеальным.
По характеру взаимодействия с окружающей средой ТДС разделяются на открытые и закрытые. Если ТДС обменивается с внешней средой только энергией, она называется закрытой (рис. 1.2, а). В открытой ТДС (рис. 1.2, б) кроме обмена энергией существует и обмен веществом (рабочим телом). Если между ТДС и внешней средой отсутствует обмен и веществом и энергией, такая система называется изолированной.
Система называется изолированной в тепловом отношении, если отсутствует теплообмен с внешней (окружающей) средой.
Если система обменивается теплом с внешней (окружающей) средой только путем теплообмена она называется изолированной в механическом отношении.
1.3. Реальный и идеальный газы.
Параметры состояния рабочего тела
В технической термодинамике при расчётах рабочих процессов в элементах ГТД с вполне удовлетворительной точностью почти всегда используют модель идеального газа вместо реального газа.
Газы, между молекулами которых отсутствуют силы взаимодействия, а сами частицы газа представляются в виде материальных точек, т.е. имеют массу, но не имеют объёма, называются идеальными.
Введение понятия модели идеального газа в термодинамике даёт возможность найти более простые аналитические зависимости между параметрами. Степень расхождения в свойствах идеальных и реальных газов зависит всякий раз от конкретных условий, в которых находится газ.
Очевидно, что реальный газ тем ближе отвечает модели идеального, чем меньше его плотность, т.е. чем меньше части газа в единице объёма. В дальнейшем при изучении процессов и явлений в ГТД газ, как рабочее тело, будет рассматриваться как идеальный.
Для количественной оценки состояния рабочего тела используют ряд величин, называемых параметрами состояния, которые имеют простой, наглядный смысл и могут быть замерены сравнительно простыми приборами.
Физические величины, характеризующие состояние системы и поддающиеся непосредственному измерению, называется параметрами состояния.
В технической термодинамике за основные параметры состояния рабочего тела (газа) принимают давление, температуру и удельный объём или плотность.
Рассмотрим параметры состояния рабочего тела.
1.3.1. Давление
Давление р по физическому смыслу представляет собой результат ударов хаотически движущихся молекул о стенки сосуда, в котором находится газ.
Давлением рабочего тела называют силу, действующую по нормали к контрольной поверхности тела и отнесённую к единице площади этой поверхности.
В соответствии с молекулярно – кинетической теорией давление газа обусловлено взаимодействием молекул рабочего тела с его оболочкой и определяется по формуле:
p = 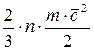 , (1.1)
, (1.1)
где n – число молекул в единице объёма, m – масса молекулы, кг; 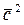 = =
= = 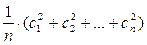 – средняя квадратичная скорость поступательного движения молекул, м/с2.
– средняя квадратичная скорость поступательного движения молекул, м/с2.
В международной системе единиц (СИ) или ГОСТ 8.417-2002 давление измеряется в Паскалях (1 Па = 1 H/м2).
Соотношения между другими единицами давления, которые используются в авиационной технике, приведены в таблице 1.2.
Таблица 1.2.
Соотношения между единицами измерения давления
| Наименование единиц | Ньютон на квадратный метр, Паскаль H/м2, Па | Бар, Бар | Килограмм сила на квадратный метр, кгс/м2 | Физическая атмосфера, атм. | Миллиметры водяного столба, мм. водян. ст. | Миллиметры ртутного столба, мм. рт. ст. |
| 1 H/м2 | 1·10-5 | 0,101972 | 0,987·10-5 | 0,101972 | 750·10-5 | |
| 1 бар | 105 | 10197,2 | 0,987 | 10197,2 | 750,06 | |
| 1 кгс/м2 | 9,80665 | 9,8·10-5 | 0,968·10-5 | 735,55·10-4 | ||
| 1 атм | 1,01325·105 | 1,01325 | 1,033·104 | 1,0332·104 | 760,00 | |
| 104 мм. водян. ст. | 0,980665·105 | 0,98066 | 104 | 0,968 | 104 | 735,55 |
| 103 мм. рт. ст. | 1,33322·105 | 1,33322 | 1,359·104 | 1,316·104 | 1,35951·104 | 103 |
Примечание: 1. Давление в мм. водян. ст. рассматривается при t = 4 °С и ускорении свободного падения g = 9,80668 м/с2 ;
2. Давление в мм. рт. ст. рассматривается при t = 4 °С и
g = 9,80665 м/с2 .
Для измерения давления в технике применяют приборы, определяющие не абсолютное, т.е. полное давление, а разность между абсолютным и атмосферным (барометрическим) давлениями.
Приборы, служащие для измерения давлений больше атмосферного называют манометрами. Они показывают избыточное давление над атмосферным. Этот избыток давления называется манометрическим давлением (избытком). Для измерения давления меньше атмосферного применяют вакуумметры, показывающие, насколько абсолютное давление меньше атмосферного. Эту недостачу давления до атмосферного называют вакуумом.
Методы измерения давления проще всего рассматривать на жидкостных приборах. На рис. 1.3 представлено измерение давления посредством жидкостного манометра.
Если давление в резервуаре больше атмосферного (рис. 1.3, а), то жидкость в правом колене трубки установится выше, чем в левом, и разность уровней будет равна h мм. Ниже сечения c–d жидкость в трубке находится в равновесии, следовательно, и в правом и в левом колене трубки в сечении c–d давления на жидкость одинаковы, а отсюда можно написать, что
ра·f = рб·f + g·ρ·f·h ,
где ра – абсолютное (полное) давление газа в резервуаре; рб – атмосферное давление по барометру; ρ – плотность жидкости; f – внутреннее сечение трубки; g – 9,80665 м/с2 – нормальное ускорение свободного падения; g·ρ·f·h – вес столба жидкости сечением f и высотой h.
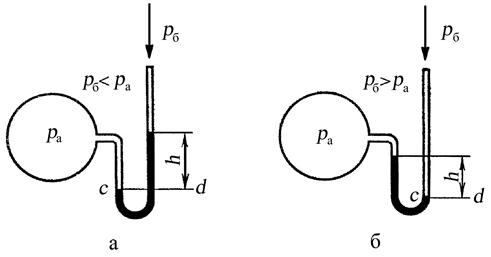
Рис. 1.3. Измерение давления жидкостным манометром
При сокращении на f получается
ра = рб + g·ρ·h,
где g·ρ·h = рм давление столба жидкости высотой h, выраженное в тех же единицах, в каких даны давления ра и рб. При этом последнее уравнение получит вид
ра = рб + рм. (1.2)
Таким образом, показание манометра определяет избыток давления в резервуаре над атмосферным, а абсолютное давление определяется формулой (1.2).
Если давление в резервуаре меньше атмосферного, то уровень жидкости будет выше в левом колене (рис. 1.3, б) и равенство давления на поверхности жидкости в сечении c–d будет выражаться уравнением
ра + g·ρ·h = рб,
а так как g·ρ·h = рв, где рв – давление, создаваемое столбом жидкости высотой h, то
ра = рб – рв. (1.3)
Следовательно, абсолютное давление газа в резервуаре в данном случае равно разности показаний барометра и вакуумметра, причем рв определяет вакуум в резервуаре.
Барометрическое (атмосферное) давление измеряется барометрами, шкала которых градуирована обычно в миллиметрах ртутного столба. Для перевода барометрического давления в Па можно пользоваться формулой
pб = 133,3·В, Па,
где В мм. рт. ст. – показание барометра.
В авиационной технике широко используются манометры для контроля давления в воздушных системах, гидросистемах, в системе смазки двигателя и др. Эти манометры установлены в кабинах экипажа воздушного судна.
Заметим, что при термодинамических расчётах используется только абсолютное давление.
1.3.2. Температура
Температура Т характеризует степень нагретости тела. По физическому смыслу температура является мерой интенсивности теплового движения молекул.
Представление о термодинамическом равновесии позволяет уточнить термодинамический смысл температуры.
С точки зрения термодинамики температура – это единственный параметр, одинаковый во всех точках нескольких систем или частей одной и той же системы в состоянии термодинамического равновесия.
Другие параметры состояния (давление, внутренняя энергия) остаются постоянными, но не обязательно одинаковыми во всех точках системы.
Важность этого положения настолько велика, что по предложению одного известного английского физика Р. Фаулера (1889–1944) оно было названо нулевым началом (законом) термодинамики.
Из термодинамического определения температуры следует, что этот параметр является функцией состояния системы, так как не зависит от начального состояния и предыстории системы, а определяется только состоянием системы в данный момент времени.
Это же свойство температуры подтверждается и её статистическим смыслом, в соответствии с которым она служит мерой средней кинетической энергии 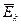 теплового движения частиц вещества:
теплового движения частиц вещества:
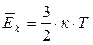 , (1.4)
, (1.4)
где к = 1,38·10-23 Дж/К – постоянная Больцмана.
Абсолютная температура Т отсчитывается по термодинамической шкале (в Кельвинах) от абсолютного нуля температуры, которому соответствует полное прекращение поступательного движения молекул. Для измерения температуры пользуются также международной практической температурной шкалой (в градусах Цельсия). Соотношение между этими шкалами выражается формулой
Т = t + 273,15 , К. (1.5)
Величина градуса по шкале Кельвина принимается равной градусу по стоградусной шкале Цельсия.
XIII Генеральная конференция по мерам и весам (1967 г. Резолюция 4) и ГОСТ 8.417-2002 с. 3, определяют термодинамическую шкалу температур посредством тройной точки воды. Как понять такое определение? Тройной точкой называется температура, при которой все три состояния, или, как говорят, все три фазы (лёд, вода, пар), находятся в равновесии. Тройная точка характеризуется давлением пара в 4,58 мм. рт. ст. и температурой 0,0075 °С (округлённо 0,01 °С). Только при этой температуре лёд, вода и пар могут находиться при одном давлении. А разве при обычном атмосферном давлении над смесью льда и воды нет пара? Есть, конечно, но давление его составляет лишь небольшую часть атмосферного давления и равняется приблизительно 4,5 мм. рт. ст. Если мы хотим воду изо льда при 0 °С и давлении в 1 атм. (760 мм. рт. ст.) превратить в пар такого же давления, то мы должны нагреть её до 100 °С (верхняя пунктирная горизонтальная линия на рис. 1.4.). При давлении ниже 4,58 мм. рт. ст. лёд переходит в пар, минуя жидкую фазу.
Разность между температурами какого-нибудь состояния в термодинамической и стоградусной шкалах составит:
273,16 – 0,01 = 273,15 °С.
Таким образом, температура исходной точки термодинамической шкалы (абсолютный нуль) по шкале Цельсия (стоградусной шкале) равна:
0 – 273,15 = – 273,15 °С.
Как правило, в повседневной жизни пишется упрощённо:
Т = (t + 273) K.
В Англии, в США и в некоторых других странах для измерения температуры принята шкала Фаренгейта (°F), в которой за 0 °F принята температура таяния смеси льда с поваренной солью, а температура таяния воды равна 212 °F и, следовательно, разность температур кипения воды и таяния льда по шкале Фаренгейта равна 212 – 32 = 180 °F.
Таким образом, 1 °F равен 100/180 = 5/9 °C.
На основании изложенного можно написать формулы пересчета температур из одной шкалы в другую:
t °C = [t °F – 32]· 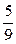 ; t °F =
; t °F = 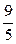 ·t °С + 32.
·t °С + 32.
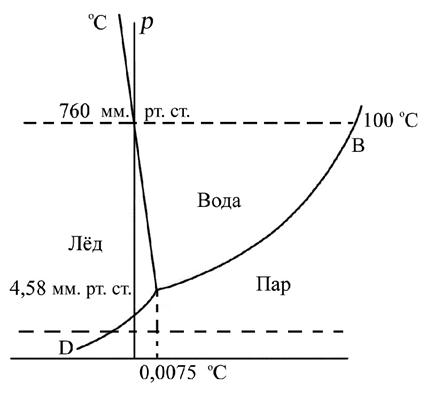
Рис. 1.4. График, иллюстрирующий тройную точку
Шкала Фаренгейта, отсчитанная от абсолютного нуля, называется шкалой Ранкина (°R) В этой шкале tо = 0 °С, Tо = 273,15 К соответствует 491,67 °R, а tk = 100 °С, Тк = 373,15 К равно 671,67 °R.
Температура измеряется с помощью термометров различных типов: жидкостных, газовых, электрических, звуковых. Например, измерение температуры газа за турбиной ГТД осуществляется с помощью электрического термометра, сигнал от которого передается на указатель температуры, размещённый в кабине пилотов.
Наряду с рассмотренными температурными шкалами применяются и другие температурные шкалы. Сравнение различных температурных шкал приведено в П. 1.
1.3.3. Удельный объём, плотность
Удельный объём υ – объём занимаемый 1 кг рабочего тела (газа) и определяется по формуле:
υ = V/m, м3/кг, (1.6)
где V – объём занимаемый газом м3;
m – масса газа, кг.
Плотностью ρ называется количество газа, заключённое в единице объёма. Следовательно, если m кг занимают объём V м3, то плотность его определяется по формуле
ρ = m/V, кг/м3. (1.7)
Из данных определений видно, что плотность газа ρ это величина обратная удельному объёму υ, т.е.
ρ·υ = 1. (1.8)
1.4. Уравнение состояния идеального и реального газов
1.4.1. Уравнение состояния идеального газа
Основные параметры рабочего тела независимо от его агрегатного состояния связаны между собой уравнением, называемым уравнением состояния, которое может быть представлено так:
f (p, υ, T) = 0. (1.9)
Уравнение (1.9) в пространстве отображает поверхность, которая характеризует всевозможные равновесные состояния химически однородной термодинамической системы (газ, жидкость). При отсутствии внешних полей (гравитационного, электрического, магнитного) число независимых параметров, однозначно определяющих равновесное состояние системы, будет равно двум из трех (p, υ, T), так как любой из этих трех параметров является однозначной функцией двух заданных.
Например, если принять за независимые переменные υ и T, то p можно выразить как функцию υ и Т, т.е. р = р (Т, υ); если же за независимые переменные принять р и Т, то удельный объём можно выразить как функцию р и Т, т.е. υ = υ (р, Т).
Таким образом, уравнение состояния устанавливает связь между давлением, температурой и удельным объёмом однородной термодинамической системы.
Наиболее простой вид уравнение состояния имеет для идеальных газов. Свойства идеальных газов, как известно, основаны на экспериментальных законах. (Законы Бойля – Мариотта, Гей – Люсака и Шарля).
Эти законы можно объединить в один, который формируется так: для данного газа произведение давления на объём в любом состоянии пропорционально его массе и абсолютной температуре.
Математическая запись этого закона выражается уравнением Клапейрона (1834 г.).
p·V = m·R·T (1.10)
Для одного кг газа уравнение (1.10) принимает вид:
p·υ = R·T (1.11)
В уравнениях (1.10), (1.11) коэффициент R имеет размерность Дж/(кг·K) и называется газовой постоянной, которая зависит от молекулярной массы газа μ.
Уравнению Клапейрона можно придать универсальную форму, если отнести газовую постоянную к одному киломолю газа.
Киломолем (кмоль) или килограммолекулой называется количество килограммов вещества, численно равное его молекулярной массе.
Обе части уравнения (1.11) умножим на массу одного киломоля μ, г/кмоль.
p·υ·μ = R·T·μ , (1.12)
где υ·μ = Vμ , 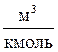 – объём одного киломоля газа;
– объём одного киломоля газа;
μ·R = Rμ , Дж/(кмоль·К) – универсальная газовая постоянная.
Известно, что идеальные газы подчиняются закону Авогадро (1811 г.), который гласит, что при одинаковых температурах и давлениях объёмы, занимаемые одним киломолем любого идеального газа, одинаковы. Измерения показали, что при нормальных атмосферных условиях (pо = 101325 Па; То = 273,15 К) один киломоль идеального газа занимает Vμ = 22,4136 м3, отсюда можно получить, что
μ·R = Rμ = 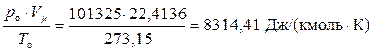
Rμ = Rун .
Таким образом, для одного киломоля идеального газа уравнение состояния будет одинаковым для всех газов:
p·Vμ = Rμ·T (1.13)
Это уравнение носит название уравнение Клапейрона – Менделеева.
С помощью формулы
R = 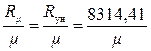 (1.14)
(1.14)
можно определить газовую постоянную R для любого газа.
Масса одного киломоля сухого воздуха находится по уравнению:
μвозд = 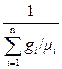 , (1.15)
, (1.15)
где gi = mi /mсм – массовая доля газа или отношение массы газа к общей массе смеси;
μi – молекулярная масса одного киломоля i-го газа в составе смеси, кг/кмоль.
Пользуясь таблицей 1.1., получаем
μвозд = 1/(0,78084/28,0134 + 0,209476/31,9968 + 0,934/39,3440 +
+ 0,0314/44,0079 + и т.д.) = 28,966 кг/кмоль.
Таким образом, газовая постоянная сухого воздуха равна
Rвозд = 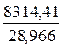 = 287 Дж/(кг·К).
= 287 Дж/(кг·К).
Рассуждая аналогичным образом можно вычислить газовую постоянную для продуктов сгорания для газотурбинных двигателей (ГТД), она получается равной
Rг = 288 Дж/(кг·К).
1.4.2. Уравнение состояния реального газа
Хотя уравнения (1.10…1.13) строго приложимы лишь к идеальным газам, они с достаточной точностью могут быть применены для решения многих задач авиационной техники, в частности для определения свойств газов и расчёта термодинамических процессов, в задачах аэродинамики летательных аппаратов, теории авиационных двигателей и др.
Впервые уравнение, которое в какой-то мере учитывает реальные свойства газов, предложил Ван–дер–Ваальс (1873 г.). Он добавил к внешнему давлению величину внутреннего молекулярного давления, которое было принято пропорциональным квадрату его плотности, т.е.
pвн. мол. = а·ρ2 ,
и отнял из общего объёма одного килограмма газа объём в, занимаемый его молекулами.
С учётом этих двух поправок и сил взаимодействия между молекулами, уравнение состояния реального газа получило вид
(p + a·ρ2) · (υ – в) = R·T. (1.16)
1.5. Понятие о термодинамическом процессе. Равновесные (обратимые) и неравновесные (необратимые) процессы
1.5.1. Равновесные (обратимые) процессы
Термодинамическая система может находиться в равновесном и неравновесном состояниях.
Система находится в термодинамическом равновесии, если при
отсутствии внешних воздействий основные свойства системы (например, давление и температура) во всех частях её одинаковы и неизменны во времени. i
Если же отдельные части тела системы обладают неодинаковыми свойствами, то такая система неравновесна. С течением времени неравновесная изолированная система станет равновесной (например, температура станет во всех её частях и телах одинаковой).
При каждом местном тепловом или механическом воздействии на
термодинамическую систему требуется определенное время релаксации (выравнивания), чтобы состояние во всех частях системы стало одинаковым.
Термодинамическим процессом называется процесс последовательного изменения состояния системы при тепловом или механическом, или одновременно тепловом и механическом воздействиях на неё извне.
В технической термодинамике процесс считается равновесным, если он протекает бесконечно медленно, под действием бесконечно малой разности температур и давлений.
Термодинамический процесс считается обратимым, если термодинамическая система, оставаясь всё время равновесной, переходит из одного состояния в другое в одном направлении и обратно через все те же промежуточные состояния, не оставляя в системе или вне её каких либо изменений.
Таким образом, для равновесных (обратимых) процессов характерны следующие особенности:
1. Давление и температуру термодинамической системы всегда можно считать равными давлению и температуре окружающей (внешней) среды;
2. Система в любой момент процесса может считаться находящейся в равновесном состоянии;
3. Количество энергии, отданное окружающей (внешней) средой системе в виде работы, всегда равно количеству энергии, воспринятой системой в том же виде;
4. Равновесный процесс протекает бесконечно медленно.
Эти особенности очень важны для термодинамики, так как они дают возможность оперировать параметрами состояния системы при анализе процессов и определять количество работы и теплоты через параметры состояния системы.
Равновесные процессы являются условным, идеализированным понятием. Однако опыт показывает, что это абстрактное понятие может быть с успехом применено не только в установлении общих закономерностей термодинамики, но и для расчёта многих реальных процессов. Таким образом, из сказанного выше можно сделать вывод: обратимый термодинамический процесс является фундаментальной моделью в термодинамике. Эта модель должна удовлетворять трём следующим условиям:
а) обратимые процессы допускают (в случае необходимости при помощи соответствующих вспомогательных средств) обратную последовательность процессов;
б) восстановление исходного состояния не требует затрат энергии;
в) обратимый процесс не должен оставлять ни в одном из участвующих тел изменений состояния системы.
1.5.2. Графическое изображение термодинамического процесса
Наглядное представление о состоянии рабочего тела термодинамической системы удобно изобразить графически в координатах “p-υ” (рис. 1.5).
1.5.3. Неравновесные (необратимые) процессы
Обратимые процессы предполагают отсутствие трения. В самом деле, если в процессе расширения рабочего тела имеется трение, то на это затрачивается часть совершаемой работы, которая переходит в эквивалентное количество тепла, воспринимаемое самим рабочим телом. Поэтому работа расширения при наличии трения будет меньше, чем при его отсутствии. Если сжимать теперь рабочее тело с целью возврата его в исходное состояние, то затрата работы на сжатие по абсолютной величине будет больше, чем при отсутствии трения, т.к. на преодоление трения затрачивается работа. Таким образом, при наличии трения работа расширения будет меньше работы сжатия до первоначального состояния. Следовательно, процесс при наличии трения является необратимым.
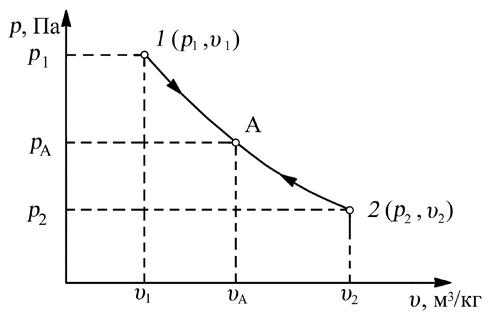
Рис. 1.5. Состояние рабочего тела в координатах “p-υ”
Точка 1 (p1 , υ1) – начальное равновесное состояние;
Точка 2 (p2 , υ2) – конечное равновесное состояние;
Точка А (pА , υА) – промежуточное равновесное состояние;
Линия 1–2 – равновесный термодинамический процесс;
Линия 2–1 – обратимый термодинамический процесс
Потеря работы при необратимых процессах, связанная с их необратимостью, называется диссипацией (рассеянием) энергии. Следует заметить, что согласно первому закону термодинамики общее количество энергии при этом не уменьшается, однако работоспособность системы из-за необратимости процесса меньше.
Трение вызывает необратимость любых механических процессов. В качестве примера можно привести течение газа или жидкости с трением; трение в потоке всегда приводит к диссипации энергии: хотя трение не уменьшает общий запас энергии потока (работа трения переходит в тепло), величина полезной работы, которую газ способен совершить при этом, становится меньше. Эффект (например, трение), делающие процессы необратимыми, называются диссипативными.
Процессы, происходящие под действием больших разностей температур и давлений, называются неравновесными или необратимыми.
Процессы, связанные с самопроизвольным переходом системы из неравновесного в равновесное состояние, также являются необратимыми. Вот некоторые примеры необратимых процессов: переход теплоты от нагретого тела к холодному; взаимное перемешивание двух различных газов, попавших в один объём; расширение газа в пустоту и др. Следует подчеркнуть, что всякий необратимый процесс характеризуется определённой направленностью. Он развивается в каком-то одном направлении и не развивается в обратном.
В течение неравновесного процесса состояние системы невозможно характеризовать определёнными значениями параметров состояния. Поэтому неравновесный процесс невозможно изображать в диаграмме состояний.
Отметим еще одну особенность неравновесных процессов. Количество энергии, переданное окружающей (внешней) средой в виде работы, не соответствует количеству энергии, воспринятому термодинамической системой в виде работы, так как в неравновесном процессе, часть работы неизбежно самопроизвольно превращается в теплоту из-за трения, которое всегда сопровождает такого рода процесс.
Подчеркнем, что при неравновесном процессе невозможно выразить количество теплоты и работы через параметры состояния, так как часть энергии, переданной внешней средой термодинамической системе в одном виде, воспринимается системой в ином виде.
Реальные процессы, протекающие в природе, технических устройствах в принципе являются неравновесными. Это объясняется тем, что изменение состояния системы, представляющее собой термодинамический процесс, может быть осуществлено только посредством внешнего воздействия путём нарушения равновесия. Однако можно представить такие условия протекания реальных процессов, когда они становятся практически равновесными (квазистатическими). Любые нарушения в равновесии системы должны быть бесконечно малыми, это может быть достигнуто медленным изменением состояния системы, т.е. медленным протеканием процесса.
Таким образом, равновесный процесс является предельным случаем неравновесного при стремлении скорости протекания последнего к нулю. Замена реального процесса равновесным позволяет для его исследования использовать термодинамические уравнения и методы анализа, что даёт весьма плодотворные результаты и часто очень точные.
В механике самопроизвольные обратимые процессы могут осуществляться в идеальных случаях. Пример – механические колебания в системах без трения. Особенность самопроизвольных термодинамических процессов состоит в том, что даже в идеальном случае они оказываются необратимыми. Например, можно представить диффузию двух идеальных газов. После их перемешивания никогда не удастся вернуть газы в исходное состояние. Или представьте себе два идеальных газа имеющих в начальном состоянии разную температуру, которые находятся в разных частях замкнутой термодинамической системы. Пусть эти части разделены абсолютно теплопроводной перегородкой. Между этими частями возникнет теплообмен, в результате которого газ, имеющий более низкую температуру, нагреется, а другой газ охладится. Однако самопроизвольно никогда не произойдёт обратного процесса – охлаждение более холодного газа и нагревание более горячего.
В заключение следует заметить, что все процессы, протекающие в природе или в технических устройствах, в той или иной мере являются необратимыми из-за конечной скорости их протекания (ведущей к неравновесности) или из-за наличия диссипативных эффектов, например – трения. Поэтому обратимые процессы по отношению к реальным необратимым являются в некотором смысле идеальными, обладающими наибольшим совершенством и отсутствием потерь работы из-за необратимости. Обратимые процессы можно рассматривать как предельные, по которым оценивается качество реальных процессов.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.1.
Определить, какое количество кислорода было израсходовано из баллона ёмкостью 40 л, если давление в нем снизилось с 196 бар до 49 бар, а температура осталась постоянной и равной 20 °С.
Решение
Прежде всего, для решения задачи размерности исходных данных надо привести в соответствии с единицами измерений международной системой СИ.
V = 40 л = 40·10-3 м3, р1 = 196 бар = 196·105 Па, р2 = 49 бар = 49·105 Па;
Т1 = t1 + 273 = 20 + 273 = 293 К.
Для решения задачи понадобится газовая постоянная кислорода. Её численное значение можно взять из таблиц или вычислить по формуле:
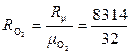 = 260 Дж/(кг·К).
= 260 Дж/(кг·К).
Определим количество кислорода m1 в баллоне при давлении р1 = 196·105 Па, используя уравнение состояния идеального газа
p1·V1 = m1· 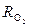 ·T1
·T1
m1 = 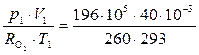 = 10,3 кг.
= 10,3 кг.
Аналогичным способом определим количество кислорода m2 в баллоне при давлении р2 = 49·105 Па, имея в виду, что V2 = V1 и T2 = T1 по условию
m2 = 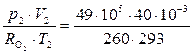 = 2,58 кг.
= 2,58 кг.
И, наконец, определяем количество израсходованного кислорода
Δm = m1 – m2 = 10,3 – 2,58 = 7,72 кг.
Проверим правильность получения размерности массы кислорода
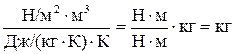 .
.
Задача 1.2.
Как изменяется давление идеального газа при увеличении абсолютной температуры в 2 раза? Концентрация молекул газа при этом не изменяется.
Решение
Воспользуемся для ответа на поставленный вопрос в задаче уравнением состояния идеального газа для 1 кг
p·υ = R·T.
Согласно уравнению при увеличении абсолютной температуры в 2 раза, при неизменной концентрации молекул газа υ = const, давление идеального газа увеличивается в 2 раза.
Задача 1.3.
Можно ли 1 кг воздуха путем сжатия и нагрева привести в состояние, характеризуемое следующими данными:
а) р1 = 147·104 Па; υ1 = 0,5 м3/кг; Т1 = 373 К.
б) р2 = 9,57·104 Па; υ2 = 0,15 м3/кг; Т2 = 50 К?
Решение
Для любого газа, в том числе и для воздуха характеризующим его свойства, является конкретное численное значение его газовой постоянной. Поэтому достаточно для каждого из состояний определить величину газовой постоянной R и сравнить с табличным значением газовой постоянной для воздуха R = 287 Дж/(кг·К).
Используя уравнение состояния идеального газа для 1 кг определим значение газовой постоянной
для состояния – а Rа = 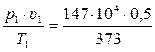 = 1970 Дж/(кг·К),
= 1970 Дж/(кг·К),
для состояния – б Rб = 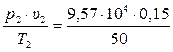 = 287 Дж/(кг·К).
= 287 Дж/(кг·К).
По полученным результатам можно сделать вывод, что 1 кг воздуха путем сжатия и нагрева можно привести в состояние б, характеризуемое параметрами р2 , υ2 , Т2 , так как Rб = Rвозд = 287 Дж/(кг·К).
Проверьте, как Вы усвоили материал
1. Назовите составные части термодинамической системы (ТДС).
2. Приведите примеры закрытых, открытых и изолированных ТДС.
3. Назовите основные параметры, определяющие состояние рабочего тела.
4. Как определяется понятие температуры в термодинамике и в молекулярно – кинетической теории?
5. Как определяется понятие давления в термодинамике и в молекулярно-кинетической теории?
6. Как называются приборы, служащие для измерения давлений больше атмосферного, меньше атмосферного?
7. Дайте определение идеальному газу.
8. Что называют уравнением состояния? Как записывается это уравнение для 1 кг идеального газа и для произвольной массы газа.
9. Каков физический смысл следующих понятий: термодинамическое равновесие, равновесное состояние, термодинамический процесс.
10. Изобразите термодинамический процесс на графике, в котором рабочее тело под воздействием внешних сил уменьшает свой объём и переходит из одного состояния в другое. Как в ходе процесса будут изменяться другие параметры рабочего тела?
11. Каковы свойства идеальных обратимых процессов?
12. Приведите примеры необратимых процессов (явлений).
13. В чём состоит принципиальное отличие идеальных механических процессов от идеальных термодинамических?
14. Воздух в аудитории из смеси различных газов: азота, кислорода, углерода, водяных паров и др. Какие из физических параметров этих газов обязательно одинаковы при тепловом равновесии?
15. Как определить численную величину газовой постоянной R данного газа?
| <== предыдущая страница | | | следующая страница ==> |
| Раздел II | | | ТЕМА 2. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ |
Дата добавления: 2014-09-08; просмотров: 1288; Нарушение авторских прав

Мы поможем в написании ваших работ!