
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ТЕМА 2. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Техническая термодинамика как наука базируется на двух основных законах природы: первом и втором законах термодинамики.
Первый закон термодинамики, это частный случай закона сохранения и превращения энергии применительно к тепловым процессам. Он лежит в основе всех термодинамических исследований, устанавливает возможность превращения различных форм энергии друг в друга и определяет в каких количественных соотношениях эти взаимные превращения осуществляются.
Прежде чем сформулировать первый закон термодинамики, ознакомимся с видами энергии рабочего тела и формами её передачи.
2.1. Внутренняя энергия рабочего тела. Изменение внутренней энергии
Газ (рабочее тело), как и всякая термодинамическая система, в любом состоянии обладает некоторым запасом энергии. Под энергией понимается форма существования материи и мера ее количественного движения.
E = m·c2 , (2.1)
где E – энергия;
m – масса;
c – скорость движения.
В термодинамике полная энергия макросистемы равна
E = Eкин+ Eпот+ U , (2.2)
где Екин – кинетическая энергия системы как целого;
Епот – потенциальная энергия системы во внешних силовых полях;
U – внутренняя энергия.
Термин “внутренняя энергия” ввели основоположники термодинамики Уильям Томсон (Лорд Кельвин) и Рудольф Клаузиус.
Величины Екин , Епот – определяются в соответствии с законами механики. А внутренняя энергия U – это энергия, заключённая в системе (рабочем теле) и включает в себя:
- кинетическую энергию поступательного, вращательного и колебательного движения молекул;
- потенциальную энергию взаимодействия молекул;
- энергию электронных оболочек атомов;
- внутриядерную энергию.
В большинстве термодинамических процессов две последние составляющие внутренней энергии остаются неизменными. Таким образом, внутреннюю энергию можно представить как сумму внутренней кинетической энергии состояния и внутренней потенциальной энергии этих частиц.
U = Uкин + Uпот , Дж (2.3)
где Дж – Джоуль является единицей измерения внутренней энергии.
1 Дж = 1 Н · 1 м
Размерность внутренней энергии для 1кг рабочего тела (газа) имеет вид:
U, Дж/кг.
В идеальных газах нет сил взаимодействия между частицами вещества, поэтому внутренняя энергия таких газов определяется только внутренней кинетической энергией.
U = Uкин , Дж/кг . (2.4)
С увеличением температуры возрастает скорость хаотического движения частиц, что ведет к увеличению внутренней кинетической энергии, следовательно, при изменении температуры рабочего тела (газа) изменяется и его внутренняя энергия.
Таким образом, внутренняя энергия идеального газа зависит лишь от его температуры, а запас внутренней энергии зависит только от состояния системы. Следовательно, внутренняя энергия U есть функция состояния рабочего тела (газа) и полностью определяется его состоянием в данный момент времени.
Если термодинамическая система находится в состоянии равновесия и отсутствует внешнее поле сил, то полная энергия системы совпадает с внутренней энергией: E = U.
Величина внутренней энергии U может быть представлена в виде двух любых независимых параметров, определяющих это состояние, или в общем случае внутренняя энергия является функцией каких либо двух параметров состояния, например
U = f (p, T) или U = f (υ, T) (2.5)
Поскольку все три параметра состояния взаимосвязаны уравнением состояния (1.11), то любой из них может быть выражен через два других.
Еще в 1806 г. опытами Гей-Люссака и Д. Джоуля было установлено, что при любых малых давлениях внутренняя энергия U практически не зависит от давления (р) и удельного объема (υ), а зависит только от температуры (Т). Позже на основе молекулярно–кинетической теории газов было показано, что внутренняя энергия U в точности зависит только от температуры для модели идеального газа (Закон Джоуля). Поэтому для рабочего тела ГТД и ДВС (воздух и продукты сгорания) с высокой точностью уравнение состояния можно записать в упрощенном виде
U = f (T). (2.6)
При исследовании термодинамических процессов вполне достаточно выяснить не конечные результаты количества внутренней энергии, а каким образом она изменилась в данном процессе, т.е. необходимо знать только изменения внутренней энергии при изменении состояния системы.
Изменение внутренней энергии 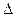 U не зависит от характера термодинамического процесса, а определяется только начальным и конечным состоянием системы (рабочего тела).
U не зависит от характера термодинамического процесса, а определяется только начальным и конечным состоянием системы (рабочего тела).
Оно равно разности внутренних энергий системы в конечном и начальном состояниях:
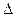 U1-2 =
U1-2 = 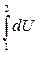 = U2 – U1 , (2.7)
= U2 – U1 , (2.7)
где U1 – внутренняя энергия рабочего тела в начальном состоянии;
U2 – внутренняя энергия рабочего тела в конечном состоянии.
В технической термодинамике и в теории ГТД и ДВС также используются не абсолютные значения внутренней энергии, а её изменения в каком-либо интервале температур Т1…Т2
ΔU1-2 = U2 – U1 = f (T2) – f (T1), (2.8)
где индекс 1 и 2 обозначены начальные и конечные значения U и Т.
Поэтому при расчётах начало отсчёта внутренней энергии, где условно принимается U = 0, может быть выбрано при произвольной температуре, которая обычно указывается в таблицах или графиках U в справочной литературе.
Из уравнения (2.8) следует, что независимо от вида энергообмена между термодинамической системой и окружающей средой в форме теплоты или механической работы порознь или совместно в любых соотношениях, но при изменении температуры газа во всех случаях на одну и ту же величину изменение внутренней энергии 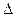 U также одинаково, несмотря на различия в изменениях υ и p.
U также одинаково, несмотря на различия в изменениях υ и p.
Так как U = f (T), поэтому производная от внутренней энергии идеального газа по температуре есть полная производная или полный дифференциал
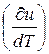 p =
p = 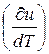 υ =
υ = 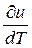 (2.9)
(2.9)
Следует отметить, что при нагревании газа возрастает энергия колебательного движения молекул. Вследствие этого на нагрев расходуется всё большее количество энергии. Поэтому величина производной 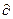 U/dT с увеличением температуры Т не остается постоянной, а возрастает с ростом Т.
U/dT с увеличением температуры Т не остается постоянной, а возрастает с ростом Т.
Количественное выражение производной 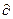 U/dT было установлено Д. Джоулем (1844 – 1845 гг.) Её называют удельной теплоёмкостью при постоянном объёме и обозначают
U/dT было установлено Д. Джоулем (1844 – 1845 гг.) Её называют удельной теплоёмкостью при постоянном объёме и обозначают
Cυ = 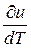 . (2.10)
. (2.10)
Если принять теплоёмкость Cυ постоянной или не зависящей от температуры, то изменение внутренней энергии в любых термодинамических процессах определяется формулой:
ΔU1-2 = U2 – U1 = Cυ ∙ (T2 – T1). (2.11)
С учетом зависимости теплоёмкости от температуры Т уравнение (2.11) примет вид
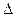 U1-2 = U2 – U1 =
U1-2 = U2 – U1 = 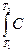 υ ср (T2 – T1), (2.12)
υ ср (T2 – T1), (2.12)
где Сυ ср – среднее значение теплоёмкости при постоянном объёме.
Какими же способами можно изменить внутреннюю энергию термодинамической системы (рабочего тела)? В термодинамике рассматриваются два таких способа.
Первый из них – это теплообмен. А другой способ изменения внутренней энергии – процесс совершения работы.
Приступим к рассмотрению вопросов, связанных с формами передачи энергии в термодинамических процессах в виде работы и теплоты.
2.2. Работа газа, как форма передачи энергии в
термодинамическом процессе
При рассмотрении простейшей ТДС отмечалось, что процесс превращения теплоты в работу сопровождается обменом энергией между источниками теплоты, рабочим телом и источником работы. Существуют две формы передачи энергии между взаимодействующими телами – в форме теплоты и в форме работы.
Работа представляет собой часть внутренней энергии системы, передаваемой в термодинамическом процессе, т.е. она является формой обмена энергии. Она также является оценкой количественной величины передаваемой энергии. Из физики известно, что механическая работа производится только при наличии движения под действием механической силы. Без движения механической работы нет, следовательно, работа является формой передачи упорядоченного, организованного движения в одном направлении. В этом можно убедиться на примере совершения работы газом при его расширении. Частицы газа, находящиеся под поршнем в цилиндре, пребывают в непрерывном хаотическом, неупорядоченном движении.
Когда газ начинает перемещать поршень, т.е. совершать механическую работу, то на беспорядочное движение частиц газа накладывается организованное движение: все частицы наряду с хаотическим движением получают некоторое смещение в направлении движения поршня и совершают работу по перемещению поршня.
В термодинамике рассматривается только механическая работа. В количественном отношении механическая работа является мерой обмена механической формой движения, т.е. мерой энергии, передаваемой в механической форме.
Работа газа в технической термодинамике обозначается буквой L и измеряется в Джоулях, а удельная работа или работа 1 кг газа обозначаются буквой L и измеряется в Дж/кг.
Выведем формулу работы, совершаемую газом, для закрытой ТДС. Поместим 1 кг газа в цилиндр с подвижным поршнем и подведем к нему некоторое количество теплоты при условии, что давление газа в цилиндре постоянное и равно давлению внешних сил (рис. 2.1.) При подведении теплоты увеличится скорость хаотического движения молекул, что приведет к возрастанию давления и температуры газа. При этом сила, действующая на поршень изнутри цилиндра, станет больше силы внешней среды, в результате чего поршень переместится (вправо), т.е. газом будет совершена работа по перемещению поршня. Величина это работы L равна произведению силы Р = р·F на путь x:
т.е. L = p·F·x, но так как F·x = υ2 – υ1, имеем L = p·(υ2 – υ1) или L = p·Δ υ (2.13)
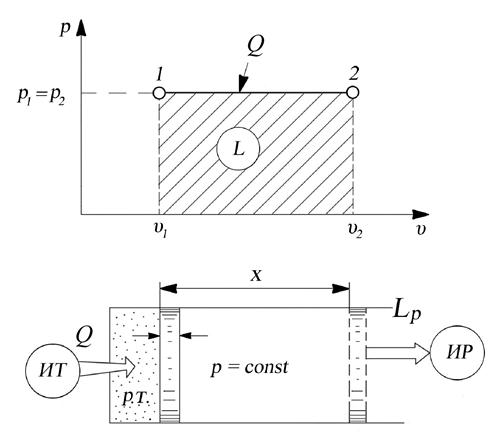 Таким образом, мы можем подсчитать работу, зная параметры состояния рабочего тела. Эта работа связана с изменением объёма, поэтому она называется работой расширения – сжатия (деформации).
Таким образом, мы можем подсчитать работу, зная параметры состояния рабочего тела. Эта работа связана с изменением объёма, поэтому она называется работой расширения – сжатия (деформации).
Рис. 2.1. К определению работы расширения–сжатия при p = const
Рассмотрим произвольный термодинамический процесс, в котором давление в течение всего процесса постоянно изменяется. Определим работу, совершаемую рабочим телом в произвольном термодинамическом процессе (рис. 2.2.).
Если подвести бесконечно малое количество теплоты dQ, произойдет бесконечно малое изменение объема dυ и будет получена элементарная работа dL, равная
dL = p·dυ (2.14)
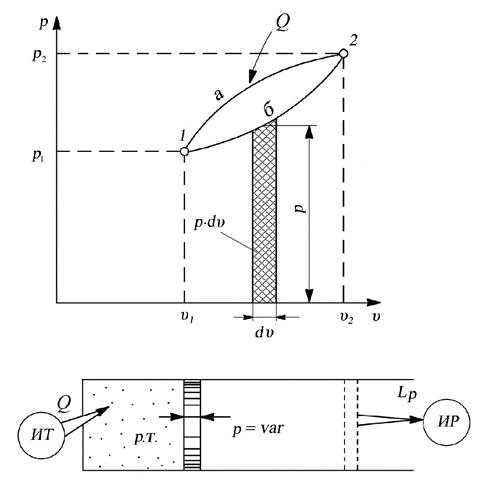
Рис. 2.2. К определению работы расширения при p = var
В общем случае давление в процессе не остается постоянным, поэтому работа в произвольном процессе 1–2 (рис. 2.2.) определяется по его формуле:
L1-2 = 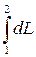 =
= 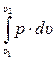 . (2.15)
. (2.15)
Для аналитического вычисления работы по уравнению (2.15) требуется знать закон изменения давления в данном процессе при изменении объёма, т.е. уравнение p = f (υ). Графическое изображение уравнения p = f (υ) называют рабочей диаграммой, так как она позволяет определить количество работы в рассматриваемом термодинамическом процессе.
Работа газа в любом термодинамическом процессе в координатах “р-υ“ изображается площадью, ограниченной линией процесса и осью объёмов. Из графического изображения работы (рис. 2.2.) видно, что ее величина зависит от пути термодинамического процесса. Так, в процессе, идущем по пути 1-а-2, работа получается больше, чем в процессе, идущем по пути 1-б-2 (рис. 2.2.). Действительно, площадь υ11а2υ2 больше площади υ11б2υ2, таким образом 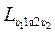 >
> 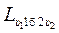 .
.
Работа в уравнении (2.15) выражена через параметры p и υ, каждый из которых по-своему характеризует обмен механической энергией. Изменение объёма, т.е. механическое перемещение границ системы, является признаком передачимеханической энергии. Величина давления в системе определяет возможность обмена механической работой: расширение (или сжатие) газа возможно только в том случае, когда давление в системе отличаются от давления в окружающей среде.
Таким образом, абсолютное давление характеризует с количественной стороны причину, вызывающую обмен механической энергией, т.е. обмен работой.
В термодинамике принято считать количество механической работы положительным, когда работа совершается термодинамической системой над окружающей средой. Применительно к газу, как рабочему телу, работа расширения газа принято считать положительной, а работа сжатия газа – отрицательной.
2.3. Теплота, как форма передачи энергии в
термодинамическом процессе
Форма обмена энергией соответствующая хаотическому, беспорядочному неорганизованному движению микрочастиц, составляющих тело, называется теплообменом, а количество энергии, переданное при теплообмене, называется количеством теплоты или теплом. Другими словами количество Q, это физическая величина характеризующая изменение внутренней энергии. Теплообмен не связан с изменением положения тела, а состоит в непосредственной передаче энергии частицами одного тела частицам другого тела.
Теплота может передаваться либо при непосредственном контакте между телом и окружающей средой (теплопроводностью, конвекцией, трением), либо на расстоянии (излучением), либо в результате осуществления химических реакций между составляющими рабочего тела (горение), причем во всех случаях возможен процесс при наличии разности температур между телами.
Во всех случаях элементарное количество теплоты dQ полученное (отданное) системой при передаче энергии в форме теплоты при изменении температуры можно определить как произведение теплоёмкости вещества на элементарную разность температур
dQ = m·С·dT, Дж (2.16)
где m – масса, а С – теплоёмкость тела.
Количество теплоты, приходящейся на 1 кг рабочего тела (газа) называется удельной теплотой и обозначается q. Измеряется в Дж/кг и определяется формулой:
q = С· 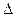 T = С·(T2 – T1) , Дж/кг (2.17)
T = С·(T2 – T1) , Дж/кг (2.17)
Таким образом, теплота и работа представляют собой две единственно возможные формы передачи энергии от одного тела к другому. Разница состоит в том, что:
- теплота является формой передачи энергии неупорядоченного движения частиц;
- работа является формой передачи энергии упорядоченного организованного движения.
Работа и теплота не содержатся, в какой либо части термодинамической системы, ни в источниках теплоты или работы, ни в рабочем теле. Работа и теплота появляются только тогда, когда осуществляется передача энергии или ее преобразование из одного вида в другой. Поэтому теплота и работа являются функциями термодинамического процесса, но не являются параметрами состояния.
2.4. Энтропия. Энтропийная “T-s” диаграмма
Долгое время признаком наличия теплообмена считали изменение температуры. Однако оказалось, что это не так. Достаточно вспомнить, что, например, при кипении воды к ней подводится большое количество теплоты, однако температура остается постоянной. При затвердевании жидкостей теплота отводится, но это не приводит к снижению температуры до тех пор, пока вся жидкость не превратится в кристаллы. В этих примерах теплообмен не приводит к изменению температуры. Наоборот, при сжатии газа в цилиндре температура газа растет, хотя теплота может даже отводиться, если стенки цилиндра холодные. В этом примере изменение температуры вызвано не теплообменом, а механической работой.
Физическая величина, изменение которой действительно является признаком теплообмена, была указана только в 1852 г. немецким физиком Р. Клаузиусом после глубокого научного анализа изменений, наблюдаемых в системе при обмене тепловой энергией. Позднее эта физическая величина получила название энтропии.
Энтропией называется физическая величина, изменение которой является признаком наличия обмена энергией в форме теплоты и обозначается буквой “s” и измеряется Дж/К.
Основная особенность энтропиикак термодинамической величины состоит в том, что она обязательно изменяется при наличии теплообмена. При подводе теплоты к термодинамической системе энтропия системы возрастает, при отводе – уменьшается. Кроме теплообмена, никакие другие воздействия на систему не могут изменить значения энтропии.
Главная трудность в понимании физического смысла энтропии состоит в том, что энтропия не оказывает воздействия на измерительные приборы и поэтому её нельзя измерить, как это делают, например, с давлением или объёмом. Впоследствии будет показано, что можно лишь вычислить изменение энтропии по изменению тех параметров, которые доступны для непосредственного измерения в системе (давления, температуры, объёма). Следовательно, энтропия является функцией состояния термодинамической системы. Связь между количеством теплоты и изменением энтропии такая же, как связь между количеством работы и изменением объёма системы.
Элементарное количество теплоты равно произведению абсолютной температуры системы на изменение энтропии системы:
dq = T·ds. (2.18)
Полное количество теплоты в каком-либо процессе определяется в виде интеграла.
Q1-2 = 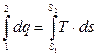 (2.19)
(2.19)
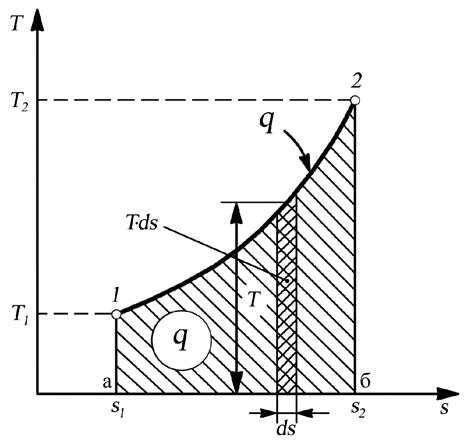 |
Рис. 2.3. Изображение теплоты в “T-s” диаграмме
Так же как и в случае работы, для аналитического вычисления количества теплоты по выражению (2.19) требуется знать уравнение, связывающее значения температуры и энтропии в каждой точке данного процесса, т. е. уравнение:
Т = f (s).
Это уравнение, будучи уравнением, связывающим между собой два параметра в процессе, также является уравнением процесса. Графическое изображение уравнения T = f (s) представляет собой так называемую энтропийную диаграмму (или тепловую диаграмму) процесса 1–2(рис. 2.3.). В “T-s” диаграмме количество теплоты выражается точно так же, как и количество работы в “p-υ” диаграмме, а именно, в виде площади под линией процесса (пл. а12б).
Определить, подводится теплота к системе или отводится от нее (т. е. определить знак количества теплоты) можно по изменению энтропии.
Уравнение (2.18)показывает, что при подводе теплоты к системе (dq > 0)энтропия увеличивается (ds > 0)и, наоборот, при отводе теплоты от системы (dq < 0), энтропия уменьшается (ds < 0).
В связи с тем, что энтропия не может быть измерена никаким прибором, выражения (2.18) и (2.19) используются в основном для графического определения количества теплоты и для теоретического анализа изменений, происходящих в термодинамических системах при взаимодействии их с окружающей средой. В частности, именно на основе уравнения (2.18), как мы увидим дальше, можно найти связь между изменением энтропии и другими параметрами состояния.
Для изолированной термодинамической системы энтропия не меняется, если в ней совершаются обратимые процессы, т.е. s = const, следовательно, ds = 0.
2.5. Зависимость количества работы и теплоты от характера термодинамического процесса
Имея выражение для количества работы и теплоты через параметры состояния системы и их графическое представление в “p-υ” и “T-s” диаграммах, легко показать, что количества работы и теплоты зависят от характера процесса. Вне процесса понятия теплоты и работы не имеют смысла, так как обозначают не запас энергии, а лишь количества энергии, передаваемые в ходе процесса. Физически характер процесса зависит от соотношения между количествами работы и теплоты, которыми система обменивается с окружающей средой, изменяя свое состояние. Аналитически различие в характере процессов выражается различием между уравнениями разных процессов.
Из формул (2.15) и (2.19) видно, что для определения количества работы и теплоты (взятие интеграла) необходимо иметь характеристики процесса в виде уравнений p = f (υ)и T = f (s).Следовательно, количества работы и теплоты зависят от характера процесса.
Графически различие в характерах процессов выражается тем, что разные процессы изображаются различными кривыми в диаграммах состояния. А так как количество работы в “p-υ” диаграмме и количество теплоты в “T-s” диаграмме представляются в виде площадей под линиями процессов, то в этих диаграммах зависимость количеств работы и теплоты от характера процесса наиболее наглядна.
В самом деле, если система рассматривается в двух определенных состояниях, характеризующихся определенными значениями параметров и функций состояния, то на диаграммах (рис. 2.4., а и 2.5,а.)эти состояния изображаются точками 1 и 2.При этом на диаграмме нет никакой линии, связывающей точки 1 и 2, а, следовательно, и площади под ней – работы (и соответственно в “T-s” диаграмме – теплоты).
Если система, обмениваясь теплотой и работой с окружающей средой, переходит из состояния 1 в состояние 2, то это изменение выражается линией на диаграмме состояния, например линией 1–2 (см. рис. 2.4., б и 2.5,б.).В этом случае количества работы и теплоты выражаются в виде площадей соответственно на “p-υ” и “T-s” диаграммах, например, площадь а12б на рис. 2.4,бопределяет работу в процессе 1–2, а площадь а12бна рис. 2.5,б – теплоту в том же процессе.
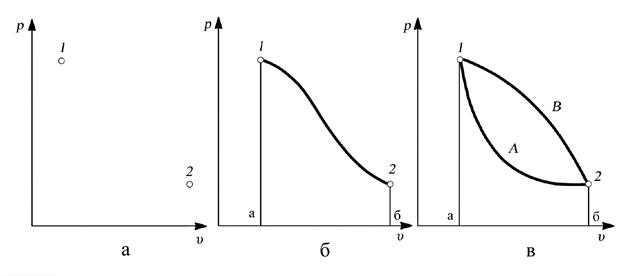 |
Рис. 2.4. Зависимость работы от характера процесса: а – знание начального и конечного состояний недостаточно для вычисления работы, б – при задании линии процесса работа выражается площадью под линией, в – при одинаковых начальных и конечных состояниях работа различна в различных процессах
Но характер изменения состояния системы между точками 1–2 может быть разным (линии 1А2 и 1В2 на рис. 2.4,в и 2.5,в), что, как уже отмечалось, зависит от соотношения между работой и теплотой при изменении состояния. Площади под линиями 1A2и 1В2оказываются различными, следовательно, различными будут и количества работы и теплоты в этих двух процессах. В примере, представленном на рис. 2.4,в,
L1A2 = 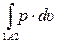 < L1B2 =
< L1B2 = 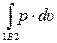
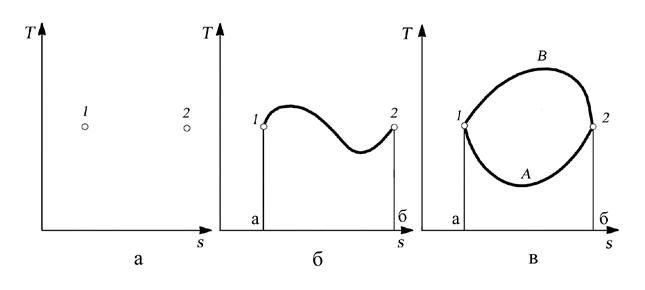
Рис. 2.5. Зависимость теплоты от характера процесса: а – знание начального и конечного состояний недостаточно для вычисления теплоты, б – при задании линии процесса теплота выражается площадью под линией, в – при одинаковых начальных и конечных состояниях теплота различна в различных процессах
В примере, представленном на рис. 2.5,в,
 q1A2 =
q1A2 = 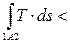 q1B2 =
q1B2 = 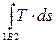
2.6. Теплоёмкость газа. Уравнение Майера. Показатель адиабаты
Теплоёмкость характеризует одно из свойств, какого–либо рабочего тела и, как известно, представляет собой количество подводимой или отводимой теплоты соответственно при нагреве или охлаждении рабочего тела на 1 Кельвин. При данных исходных параметрах состояния (Т, р или Т) теплоемкость 1 кг рабочего тела определяется в бесконечно малом интервале температур dT
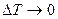 C = lim
C = lim 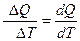 , Дж/(кг·К). (2.20)
, Дж/(кг·К). (2.20)
Эта теплоёмкость, в основном применяемая при расчётах, является удельной массовой, которую для краткости будем называть просто теплоёмкостью (заметим, что существуют и другие удельные теплоёмкости – единицы объёма или одного моля, но они используются редко).
Теплоёмкость зависит от трех основных факторов. Прежде всего, от природы вещества. Газ, жидкость, твёрдое тело естественно имеют своё определённое и конкретное значение теплоёмкости, характерное только данному веществу. Например, теплоёмкость воды в 4 раза больше, чем теплоёмкость воздуха, теплоёмкость водорода в 14,5 раз больше, чем теплоёмкость воздуха и в 3,5 раза больше, чем теплоёмкость воды и т.д.
Второй фактор – это исходные параметры состояния, при которых теплоёмкость определяется. Для газов (рабочих тел ГТД и ДВС) теплоёмкость зависит практически только от температуры С = f (T). Заметим, что у идеальных газов теплоёмкость от температуры не зависит. Но у рабочих тел ГТД и ДВС, хотя и близких к идеальным газам, влияние температуры все, же заметно. Так, в характерных для ГТД диапазонах изменения температуры воздуха от ~ 250 до 800 К и продуктов сгорания от 700 до 1 600 К теплоёмкости возрастают соответственно примерно на 10 % и на 15 %. Условие С = const принимают лишь при весьма приближённых расчётах. Поэтому будет учитываться зависимость от температуры и теплоёмкости и также других, связанных с ней и рассматриваемых ниже параметров. Но влияние давления и удельного объёма при не очень высоких давлениях до ~ (70·105…100·105 Па) ничтожно мало.
С учётом зависимости “С” от Т конечное количество теплоты Q подводимой к единице массы рабочего тела при его нагреве (или отводимой при охлаждении) в конечном интервале температур 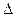 Т, определяется из уравнения (2.20)
Т, определяется из уравнения (2.20)
Q1-2 = 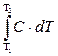 = Ccр·(T2 – T1), (2.21)
= Ccр·(T2 – T1), (2.21)
где индексами 1 и 2 обозначены начальное и конечное состояние рабочего тела; Сср– среднее значение теплоемкости в интервале температур Т1…Т2.
С достаточной точностью (хотя и приближённо) Ссрможет быть определена как среднее арифметическое теплоёмкостей (иногда их называют истинными в отличие от средней) при температурах Т1 и Т2.
Ccp = 0,5·[C (T1) + C (T2)] (2.22)
Значение С = С (Т)приводятся в справочниках в виде таблиц или графиков.
Третий фактор, влияющий на теплоёмкость, относится к сжимаемым рабочим телам – газам. Рассмотрим, в чем проявляется влияние этого фактора.
 Предположим, что имеется жёсткая закрытая термодинамическая система неизменного объёма, приведённая на рис. 2.6., а в виде цилиндра, закрытого неподвижным поршнем. В цилиндре содержится 1 кг рабочего тела. Поэтому не изменяется так же удельный объём , но давление изменяется, например, при подводе теплоты возрастает.
Предположим, что имеется жёсткая закрытая термодинамическая система неизменного объёма, приведённая на рис. 2.6., а в виде цилиндра, закрытого неподвижным поршнем. В цилиндре содержится 1 кг рабочего тела. Поэтому не изменяется так же удельный объём , но давление изменяется, например, при подводе теплоты возрастает.
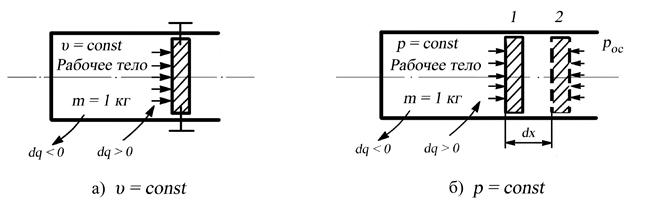 |
Рис. 2.6. К определению теплоёмкости рабочего тела
при υ = const (a), p = const (б)
Таким образом, осуществляется только один вид энергообмена – теплообмен. Истинная теплоёмкость при постоянном объёме определяется уравнением (2.20), в котором для данного случая соответствующие величины снабжены индексом υ
С υ = 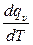 (2.23)
(2.23)
Сохраняются и уравнения (2.21) и (2.22) также с индексами υ т.е. qυ1-2и Cυ ср.
Теперь, пусть система на рис. 2.4,б оставаясь закрытой, станет нежёсткой – поршень в цилиндре может свободно перемещаться в обе стороны. Тогда, например, при подводе теплоты (dq > 0) и нагреве рабочего тела давление остается постоянным, но газ расширяется, и его удельный объём возрастет на величину dυ = F·dx,где F – площадь поршня. Осуществляются оба вида энергообмена – теплообмен и работа изменения объёма, определяемая уравнением (2.14) при бесконечно малом перемещении поршня и (2.15) при конечном перемещении, причем при р = const Lυ = р·(υ2 – υ1).
В результате подводимая к термодинамической системе теплота затрачивается и на нагрев газа и на работу термодинамической системы над окружающей средой (при отводе теплоты все описанные явления происходят в обратном направлении также при р = const). Обозначим бесконечно малую теплоту, отводимую термодинамической системе в процессе р = const с индексом р, dqр . По аналогии с уравнением (2.23)истинная теплоёмкость при постоянном давлении равна
Ср = 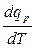 . (2.24)
. (2.24)
Поскольку dqp > dqυ из–за наличия работ изменения объёма dLυ ,то Ср > Cυ. В уравнениях (2.21) и (2.22) соответствующие величины также снабжаются индексом р т.е. qp1-2 и Cp cp.
При теплообмене параметры состояния газа р и υ по-разному изменяются в жёсткой и нежёсткой термодинамических системах, соответственно υ = const, р = var и р = const, υ = var. Но на количество поглощаемой непосредственно только газом теплоты (или отводимой от газа) это не влияет, поскольку, как отмечалось ранее, теплоёмкость газов практически не зависит от параметров состояния р и υ, а только от температуры Т. Поэтому в жёсткой (υ = const) и нежёсткой (р = const) термодинамических системах при одинаковых изменениях, температуры в данном случае бесконечно малых dT газ поглощает (или отдает) одинаковое количество теплоты dqυ. С учётом уравнения (2.14) количество теплоты, подводимой к нежёсткой термодинамической системе (а не только) определяется суммой
dqp = dqυ + p·dυ.(2.25)
Продифференцируем уравнение состояния (1.11)
d(pυ) = υ·dp + p·dυ = R·dT . (2.26)
В данном частном случае для системы р = const это уравнение упрощается, т.к. dp = 0, поэтому имеем:
p·dυ = R·dT . (2.26′)
Используя полученное уравнение (2.26′), а так же уравнения (2.23) и (2.24) из уравнения (2.25) получим
Cp = Cυ + R или Ср – Cυ = R. (2.27)
Это уравнение, связывающее Ср , Cυ и R называются уравнением Майера. Приведем порядок величин, входящих в это уравнение, например, для воздуха при стандартной температуре 288 К (15 °С): Ср = 1005 Дж/(кг·К), Cυ = 718 Дж/(кг·К), R = 287 Дж/(кг·К). Теплоёмкости Ср и Cυ зависят от температуры, а их разность численно равная значению газовой постоянной R от температуры не зависит. В этом и состоит физический смысл газовой постоянной R, которая численно равна величине работы, совершенной газом массой в 1 кг при изменении температуры в 1 К при постоянном давлении.
В термодинамике и при термодинамических расчетах ГТД и ДВС широко используется отношение теплоёмкостей
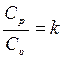 , (2.28)
, (2.28)
которое называется показанием адиабаты. Сущность этого термина выяснится из дальнейшего изложения, хотя, казалось бы, что Ср и Cυ никакого отношения к адиабатной системе не имеют.
Показатель адиабаты, как и теплоёмкости, зависит от вида газа и от температуры. Поскольку с ростом температуры обе теплоёмкости Ср и Cυ возрастают, то зависимость “k” от температуры получается довольно слабой, причём убывающей по Т. Например, для воздуха при Т = 288 К показатель адиабаты k = 1,401, а при Т = 800 К (527 °С) – k = 1,353; для продуктов сгорания при Т = 700 К (427 °С) – k = 1,350, а при Т = 1 500 К (1 227 °С) – k = 1,295. В приближённых расчётах обычно принимают: для воздуха k = 1,4, для продуктов сгорания k = 1,33.
Из уравнений (2.27) и (2.28) получаются следующие соотношения, которые часто используются при расчётах.
Ср = 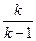 ·R (2.29)
·R (2.29)
Сυ = 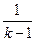 ·R (2.30)
·R (2.30)
2.7. Энтальпия
Энтальпия (теплосодержание) представляет собой сумму внутренней энергии (U) и энергии давления (p·υ), обозначаются буквой (i)
i = U + p·υ , Дж/кг (2.31)
Учитывая, что p·υ = R·T , имеем
i = U + R·T , Дж/кг. (2.32)
Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния ТДС, и может быть представлена в виде функции двух любых параметров состояния:
i1 = f 1(p, υ); i2 = f 2(p, T); i3 = f 3(υ, T); (2.33)
из изложенного не видно, какой смысл имеет введение этого нового параметра состояния. Но в дальнейшем мы убедимся в том, что энтальпия играет решающую роль в термогазодинамических расчётах теплоэнергетических установок, которыми являются ГТД и ДВС.
Как было отмечено в отношении внутренней энергии, используются не абсолютные значения внутренней энергии, а их разности в заданном интервале температур. Аналогично для энтальпии тоже не используется абсолютные значения, а важно знать их разность в заданном интервале температур, т.е. изменение энтальпии ( 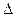 i1-2) в данном термодинамическим процессе. С учётом уравнения (2.32) получим выражение для определения изменения энтальпии
i1-2) в данном термодинамическим процессе. С учётом уравнения (2.32) получим выражение для определения изменения энтальпии
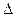 i 1-2 = i 2 – i 1 =
i 1-2 = i 2 – i 1 = 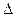 U1-2 + R·
U1-2 + R· 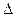 T (2.34)
T (2.34)
Начало отсчета энтальпии может быть выбрано при любой температуре, как правило, равной той, при которой условно принимается Uисх = 0. Но при этой температуре i ≠ 0, а как видно из уравнения (2.32) i исх = R·Tисх.
При бесконечно малых изменениях dU и dT из уравнения (2.10) и (2.34) следует, что
di = dU + R·dT = (Cυ+R)·dT,
а учитывая уравнение (2.27) окончательно получим
di = Cp·dT.(2.35)
При конечных изменениях этих величин, имея в виду зависимость от Т, по аналогии с уравнением (2.12) можно записать
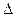 i1-2 = i2 – i1=
i1-2 = i2 – i1= 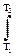 Cp · dT = Cp cp·(T2 – T1) , (2.36)
Cp · dT = Cp cp·(T2 – T1) , (2.36)
где Ср ср определяется уравнением (2.22) с индексом “р”.
Отсюда следует, что изменение энтальпии при переходе газа из одного состояния “1” в другое “2” равно количеству подводимой (или отводимой) теплоты в интервале Т1…Т2 при постоянном давлении, причем независимо от фактического перехода при любом характере изменения давления.
Из вышеизложенного можно сделать важный вывод, что энтальпия характеризует способность рабочего тела (движущегося газа) совершать работу за счёт внутренней (тепловой) энергии и энергии давления.
2.8. Техническая работа (работа движущегося газа)
Элементарная работа 1 кг газа в открытой ТДС при подводе бесконечно малого количества теплоты будет состоять из работы расширения–сжатия pdυ и приращения работы проталкивания d(pυ)
dLтехн = p·dυ – d(p·υ) . (2.37)
Приращение d(pυ) взято со знаком минус, так как эта работа совершается внешними силами над газом. Учитывая, что d(pυ) = p·dυ + υ·dp, получаем
dLтехн = – υ·dp.
Следовательно, для произвольного процесса
Lтехн = – 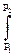 υ·dp (2.38)
υ·dp (2.38)
Это выражение называют технической работой или работой движущегося газа. В координатах “p-υ” она изображается площадью, ограниченной линией процесса и осью давлений (рис. 2.7.).
Таким образом, величина технической работы эквивалентна площади фигуры p112p2 (рис. 2.7.).

Рис. 2.7. К определению работы движущегося газа
Подчеркнём, что техническая работа – эта та работа, которая может быть совершена только в открытой термодинамической системе, и её не следует смешивать с работой расширения газа, совершаемой в закрытой системе. Различие между технической работой и работой расширения объясняется тем, что в открытой системе работа затрачивается не только на деформацию газа (сжатие или расширение), но и на ввод (или вывод) массы, а так же на изменение кинетической энергии движущегося газа.
Знак технической работы определяется знаком величины (–dp). Для процесса 1–2 (рис. 2.7.), осуществляемого с понижением давления (dp < 0), техническая работа будет положительна, так как (–dp) положительна.
2.9. Содержание и уравнение первого закона термодинамики
 В середине прошлого века произошла первая естественнонаучная революция в истории цивилизации. Она была связана с установлением закона сохранения энергии. Этот закон оказался универсальным, применимым не только к механическим процессам, но и к тепловым, и вообще, ко всем физическим процессам.
В середине прошлого века произошла первая естественнонаучная революция в истории цивилизации. Она была связана с установлением закона сохранения энергии. Этот закон оказался универсальным, применимым не только к механическим процессам, но и к тепловым, и вообще, ко всем физическим процессам.
Сейчас, конечно, никто не сомневается в том, что закон сохранения энергии имеет универсальный характер. Однако более 150 лет назад большинство физиков обобщение закона сохранения энергии, справедливого для механических явлений, на тепловые явления считали метафизическими измышлениями.
Универсальный характер фундаментального закона сохранения энергии проявился даже в том, что к его открытию причастны три знаменитых исследователя совершенно разных областей естествознания: Р. Майер, Дж. Джоуль и Г. Гельмгольц.
Среди них лишь Г. Гельмгольц – профессиональный физик-теоретик в современном понимании этого слова; Р. Майер – в большей мере философ, имеющий медицинское образование. Экспериментатором среди этих ученых был лишь Дж. Джоуль.
Закон сохранения энергии – один из самых общих принципов физики и всего естества знаний. За все годы после его открытия не было обнаружено ни одного явления природы, в котором наблюдалось бы его нарушение.
Данный фундаментальный закон природы гласит, что энергия не исчезает и не возникает вновь, а лишь переходит из одного вида в другой в строго эквивалентных количествах. Важно подчеркнуть, что закон сохранения и превращения энергии утверждает не просто сохранение энергии, а её сохранение при превращениях из одной формы в другую.
Принцип эквивалентности теплоты и работы лежит в основе первого закона термодинамики, который представляет собой частный случай всеобщего закона сохранения и превращения энергии применительно к процессам, сопровождающимся тепловыми явлениями.
Получим уравнение первого закона термодинамики. Пусть, например, к рабочему телу, заключённому в цилиндре с подвижным поршнем (рис. 2.6,б) подведено некоторое количество теплоты Q. Это приведет к повышению температуры рабочего тела, следовательно, его внутренняя энергия изменится на величину 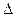 U. Кроме того, рабочее тело, расширяясь, перемещает поршень из положения 1 в положение 2 и совершает работу L против внешних сил. На основании закона сохранения и превращения энергии можно записать:
U. Кроме того, рабочее тело, расширяясь, перемещает поршень из положения 1 в положение 2 и совершает работу L против внешних сил. На основании закона сохранения и превращения энергии можно записать:
Q = 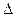 U + L , Дж. (2.39)
U + L , Дж. (2.39)
Соотношение (2.39) представляет собой математическое выражение первого закона термодинамики в самой общей форме.
Первый закон термодинамики гласит: “Подведенное извне количество теплоты Q к рабочему телу, в общем случае расходуется на увеличение его внутренней энергии 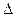 U и совершение работы расширения L против внешних сил”.
U и совершение работы расширения L против внешних сил”.
Из первого закона термодинамики следует, что если в каком либо процессе рабочее тело получает (или отдает) тепло Q, совершает работу L и его внутренняя энергия изменяется на величину 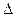 U, то алгебраическая сумма этих величин должна ровняться нулю. Отнеся в уравнении (2.39) все величины к 1 кг массы рабочего тела, получим
U, то алгебраическая сумма этих величин должна ровняться нулю. Отнеся в уравнении (2.39) все величины к 1 кг массы рабочего тела, получим
q = 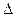 U + L, Дж/кг (2.40)
U + L, Дж/кг (2.40)
или в дифференциальной форме
dq = dU + dL (2.41)
или dU = dq – dL (2.42)
Из первого закона термодинамики следует, что если система (тело) является изолированной, т.е. не обменивается энергией с окружающей средой (Q = 0, L = 0), то её внутренняя энергия не меняется ( 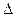 U = 0). Иначе, внутренняя энергия изолированной системы постоянна (U = const).
U = 0). Иначе, внутренняя энергия изолированной системы постоянна (U = const).
Изменение энергии системы (тела) возможно лишь при энергообмене с окружающей средой, т.е. при подводе (или отводе) к системе теплоты или работы.
Первый закон термодинамики отрицает возможность создания вечного двигателя, который совершал бы механическую работу без использования энергии (его называют вечным двигателем первого рода).
Действительно, если механическое устройство не использует «свою» внутреннюю энергию ( 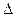 U = 0) и не получает извне количество теплоты (Q = 0), то и работа системы L = 0.
U = 0) и не получает извне количество теплоты (Q = 0), то и работа системы L = 0.
В связи с этим первый закон можно рассматривать как принцип запрета perpetuum mobile (другая формулировка первого закона термодинамики).
Таким образом, первый закон термодинамики позволяет определить количественные соотношения при взаимном преобразовании тепловой энергии в другие виды энергии. Он имеет большое практическое значение, так как используется при термодинамических расчетах элементов ГТД и двигателя в целом.
Аналитическое выражение первого закона термодинамики (2.42) в применении к равновесным процессам может быть представлено через параметры состояния системы [используя полученные ранее выражения (2.14) dL = p·dυ и (2.18) dq = T·ds] в виде
dU = T·ds – p·dυ. (2.43)
Получим запись первого закона термодинамики через энтальпию. Для этого продифференцируем уравнение (2.31) i = U + p·υ и выразим dU через уравнение (2.42) dU = dq – dL и (2.43) dU = T·ds – p·dυ:
di = dU + d(pυ) = dU + p·dυ + υ·dp = (dq – p·dυ) + p·dυ + υ·dp;
и окончательно получим:
di = dq + υ·dp = T·ds + υ·dp.(2.44)
Уравнение (2.44) представляет собой запись первого закона термодинамики через энтальпию. Это уравнение широко используется при анализе открытых термодинамических систем, каковыми например, являются отдельные модули ГТД, так и газотурбинный двигатель в целом.
2.10. Чистые вещества и смеси газов
В термодинамике принято называть "чистыми" вещества, состоящие из одинаковых молекул или атомов. Применительно к газам это, например, азот (N2), кислород (О2), углекислый газ (СО2), водяной пар (Н2О). Перегретый водяной пар, содержащийся и в воздухе, и в продуктах сгорания, по существу также является газом.
Каждый “чистый” газ, который будем обозначать индексом “i”, имеет свою молекулярную массу μi , газовую постоянную Ri = 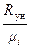 (см. формулу 1.14) и теплоёмкости Cpi и Cυi . Например, у азота
(см. формулу 1.14) и теплоёмкости Cpi и Cυi . Например, у азота 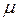 i = 14, у кислорода
i = 14, у кислорода 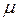 i = 32, у углекислого газа μi = 44. Поэтому существенно различаются их газовые постоянные и теплоёмкости.
i = 32, у углекислого газа μi = 44. Поэтому существенно различаются их газовые постоянные и теплоёмкости.
Рабочие тела ГТД и ДВС являются смесью “чистых” газов. Воздух (сухой) можно считать смесью двух газов – азота (~ 79 %) и кислорода (~ 21 %), поскольку содержание других газов ничтожно мало. Продукты сгорания могут иметь разный количественный состав “чистых” газов – азота, кислорода, углекислого газа, водяного пара и окиси углерода. Относительное содержание этих газов зависит от количества, впрыскиваемого в камеру сгорания топлива на 1кг воздуха, что в свою очередь определяет конечную температуру продуктов сгорания.
Задачей данного вопроса является определение необходимых при расчете ГТД и ДВС газовой постоянной и теплоёмкостей смеси газов (Rсм, Ср см, Cυ см) по значениям этих величин для “чистых” газов, составляющих смесь (Ri, Сpi , Сυi).
Относительное количество каждого “чистого” компонента газа определяется массовой долей – массой данного газа в 1 кг смеси
gi = 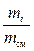 , (2.45)
, (2.45)
где mi – масса i–го компонента газа;
mсм – масса смеси газов.
Используются также мольные доли, но мы их не будем рассматривать. Поскольку mсм = 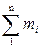 , где n – число “чистых” газовых компонентов, то
, где n – число “чистых” газовых компонентов, то
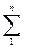 gi =
gi = 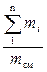 = 1 (2.46)
= 1 (2.46)
Согласно уравнению (2.20)бесконечно малое количество теплоты dq поглощённой (или отданной) 1 кг смеси при нагреве (или охлаждении) на бесконечно малую температуру равно:
dq = Cсм·dT,
где Ссм – истинная теплоёмкость смеси.
Это же количество теплоты можно представить как сумму бесконечно малых значений теплоты dq; каждого компонента массой g; в 1 кг смеси при изменении температуры также на dT одинаковой для всех компонентов, т.е.
dq = Ссм·dT = ( 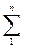 giCi)dT,
giCi)dT,
где Ci – истинная теплоёмкость данного компонента “чистого” газа.
Следовательно, искомая теплоёмкость смеси равна
Cсм = 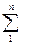 giCi .(2.47)
giCi .(2.47)
Это уравнение справедливо и при постоянном давлении.
Перейдем к определению газовой постоянной смеси, используя уравнение Клапейрона (1.11). Кроме того из курса физики известен закон Дальтона, согласно которому сумма парциальных давлений каждого газа pi , в смеси равна давлению смеси pсм
pсм = 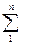 pi . (2.48)
pi . (2.48)
Напомним, что парциальным называется то давление pi, которое имел бы каждый i–й газ, будь он один в объёме смеси Vсм при температуре Т. В точности уравнения (1.11) и (2.48) справедливы для идеальных газов. Но для реальных газов при не очень высоких давлениях не только уравнение (1.11), но и (2.48) имеют очень малую погрешность.
Парциальное давление pi , которое создавал бы каждый i–ый газ, определяется по формуле
pi = ri · p, (2.49)
где ri – объёмная доля i–го компонента газа;
p – значение общего давления смеси.
Запишем уравнение Клапейрона (1.11) для 1 кг смеси
pсм · υсм = Rсм ·Tсм , (2.50)
и n уравнений для каждого из её компонентов
pi · υi = gi · Ri · Tсм , (2.51)
где i изменяется от 1 до n.
Просуммируем n уравнений (2.51)с учетом уравнения Дальтона (2.48)
pсм · υсм = Tсм 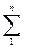 gi · Ri . (2.52)
gi · Ri . (2.52)
Приравнивая правые части уравнений (2.50) и (2.52)получим искомую зависимость газовой постоянной смеси от массовых долей gi и газовых постоянных компонентов, т.е. “чистых” газов
Rсм = 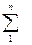 gi·Ri .(2.53)
gi·Ri .(2.53)
Имея в виду (уравнение 1.14), что Ri = 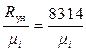 , Дж/(кг·К) получим другой вид этого уравнения
, Дж/(кг·К) получим другой вид этого уравнения
Rсм = 8314 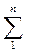
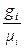 , Дж/(кг·К) . (2.54)
, Дж/(кг·К) . (2.54)
Таким образом, для определения газовой постоянной смеси Rсм необходимо знать массовые доли компонентов газа gi в смеси и молекулярные массы одного киломоля μi каждого i–го газа в составе смеси.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 2.1.
Выхлопные газы двигателя внутреннего сгорания имеют следующий объёмный состав: углекислого газа 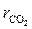 = 14 %, кислорода
= 14 %, кислорода  = 2 %, азота
= 2 %, азота 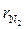 = 79 %, окиси углерода
= 79 %, окиси углерода 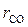 = 2 %. Найти условную молекулярную массу, газовую постоянную плотность смеси при 500 °С и 720 мм. рт. ст.
= 2 %. Найти условную молекулярную массу, газовую постоянную плотность смеси при 500 °С и 720 мм. рт. ст.
Решение
Определим условную молекулярную массу смеси газов μсм по формуле:
μсм = 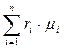 ,
,
где ri – объёмные доли компонентов выхлопных газов;
μi – молекулярные массы компонентов выхлопных газов в кг/кмоль.
Таким образом, условная молекулярная масса смеси газов вычисляется следующим образом:
μсм = 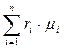 =
= 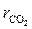 ·
· 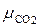 +
+  ·
· 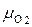 +
+ 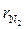 ·
· 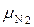 +
+ 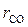 ·
· 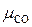 =
=
= 0,14·44 + 0,05·32 + 0,79·28 + 0,02·28 = 30,45 кг/кмоль.
Теперь используя формулу (1.14) можно определить газовую постоянную смеси Rсм
Rсм = 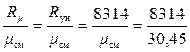 = 273 Дж/(кг·К).
= 273 Дж/(кг·К).
Проверим правильность получения размерности газовой постоянной смеси:
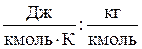 = Дж/(кг·К).
= Дж/(кг·К).
Определим плотность газов ρо при нормальных физических условиях [pо =101325 Па (760 мм. рт. ст.), То = 273,15 К], зная что 1 киломоль газа в этих условиях занимает объём равный Vμ = 22,41 м3/кмоль.
Тогда
ρо = 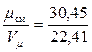 = 1,36 кг/см3.
= 1,36 кг/см3.
Проверим правильность получения размерности плотности газа:
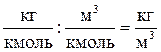 .
.
Для определения плотности смеси газов ρсм по условиям задачи при Т = 773 К (500 °С) и p = 720 мм. рт. ст. запишем уравнение состояния газов для этого состояния и уравнение состояния при нормальных физических условиях
p·υсм = p· 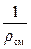 = R·T – уравнение для заданных условий (Т = 773 К и р = 720 мм. рт. ст.),
= R·T – уравнение для заданных условий (Т = 773 К и р = 720 мм. рт. ст.),
po·υo = po· 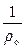 = R·To – уравнение для нормальных физических условий (Тo = 273,15 К и рo = 760 мм. рт. ст.).
= R·To – уравнение для нормальных физических условий (Тo = 273,15 К и рo = 760 мм. рт. ст.).
Откуда имеем:
ρcм = ρо· 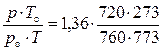 = 0,455 кг/м3.
= 0,455 кг/м3.
Проверим правильность получения размерности плотности смеси газов:
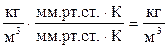 .
.
Таким образом выхлопные газы при 500 °С и 720 мм. рт. ст. имеют условную молекулярную массу μсм = 30,45 кг/кмоль; газовую постоянную Rсм = 273 Дж/(кг ·К) и плотность ρсм = 0,455 кг/м3.
Задача 2.2.
Определить состав генераторного газа в массовых процентах и парциальные давления компонентов при общем давлении смеси 760 мм. рт. ст., если газ имеет следующий состав в объёмных процентах: водорода Н2 = 15 %; окиси углерода СО = 27 %; углекислого газа СО2 = 8 %; азота N2 = 50 %.
Решение
По атомным массам элементов определим молекулярные массы газов, входящих в смесь (округлённо): 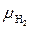 = 2·1 = 2,
= 2·1 = 2, 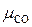 = 12 + 16 = 28,
= 12 + 16 = 28, 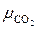 = 12 + 2·16 = 44,
= 12 + 2·16 = 44, 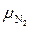 = 2·14 = 24.
= 2·14 = 24.
Условную молекулярную массу смеси μсм определим по формуле (смотрите задачу 2.1)
μсм = 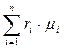 =
= 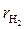 ·
· 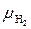 +
+ 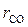 ·
· 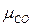 +
+ 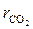 ·
· 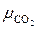 +
+ 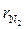 ·
· 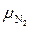 =
=
= 0,15·2 + 0,27·28 + 0,08·44 + 0,50·28 = 25,37 кг/кмоль.
Массовые доли компонентов газа gi находятся по формуле:
gi = 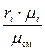 ;
;
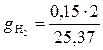 = 0,012;
= 0,012;
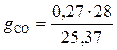 = 0,298;
= 0,298;
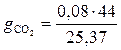 = 0,138;
= 0,138;
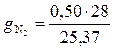 = 0,552 .
= 0,552 .
Проверим правильность полученных значений массовых долей компонентов. Сумма полученных значений должна быть равна единице, т.е. 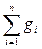 = 1:
= 1:
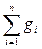 =
= 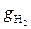 +
+ 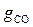 +
+ 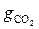 +
+ 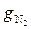 = 0,012 + 0,298 + 0,138 + 0,552 = 1,000.
= 0,012 + 0,298 + 0,138 + 0,552 = 1,000.
Следовательно, массовый состав газа в процентах будет следующим: водорода – Н Дата добавления: 2014-09-08; просмотров: 1140; Нарушение авторских прав
<== предыдущая страница
|
следующая страница ==>
ТЕМА 1. ГАЗ, КАК РАБОЧЕЕ ТЕЛО ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ | ТЕМА 3. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ

Мы поможем в написании ваших работ!