ТЕМА 3. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ

3.1. Последовательность и объём расчёта термодинамических процессов

В тепловых двигателях при их работе протекают разнообразные термодинамические процессы. Целью изучения термодинамических процессов является установление закономерностей изменения параметров состояния ТДС и особенностей преобразования энергии в этих процессах.

Знание указанных закономерностей имеет важное значение для понимания процессов, протекающих в элементах ГТД и ДВС.

Анализ (или расчёт) термодинамических процессов производится обычно в следующей последовательности:

1. Определяют уравнение процесса: исходя из условий протекания процессов и используя уравнение состояния идеального газа, находят уравнения процесса в виде зависимостей

p = f (υ); T = f (υ); T = f (p).

2. Определяют закон изменения параметров на основании уравнения процесса и уравнения состояния, используя известные по условиям задачи значения параметров состояния в начале процесса (p₁, υ₁, T₁), в конце процесса (p₂, υ₂, T₂), а если требуется – то и в промежуточных состояниях.

3. Осуществляют графическое построение процесса в рабочей “p-υ” диаграмме и тепловой “T-s” диаграмме.

4. Определяют величины, входящие в первый закон термодинамики.

q = ∆U + L; T∙∆s = ∆U + pdυ

а) q = ;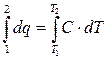

б) ∆U = ;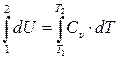

в) L = ;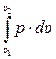

г) ∆s_1-2 = 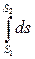= s₂ – s₁.

5. Определяют закон распределения энергии (α) для данного процесса по формуле α = ∆U/q.

Все величины, указанные в пунктах 2 и 4 могут, найдены как аналитически по уравнениям, так и графически с помощью рабочей “p-υ” диаграммы и тепловой “T-s” диаграммы. Поэтому любой расчёт процесса всегда сопровождается графическим построением процесса в этих координатах.

3.2. Изохорный процесс: определение, осуществление и исследование

Термодинамический процесс, протекающий при постоянном объёме (удельном объёме) рабочего тела, называется изохорным (от греческих слов изос – равный и хора – пространство).

В авиационной технике, процессы близкие к изохорным протекают:

- в кислородной и воздушных системах воздушного судна при изменении высоты полёта;

- в отдельных элементах конструкции самолётов и вертолётов: в пневматиках колёс, в амортизационных стойках, в бортовых баллонах со сжатыми газами при изменении температуры окружающей среды;

- в камерах сгорания поршневых двигателей.

3.2.1. Исследование изохорного процесса

1. Условие протекания процесса и есть уравнение процесса

υ = const. (3.1)

Используя уравнение состояния идеального газа, получим уравнение изохорного процесса через параметры состояния

p = 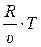= (const)·T или p = f (T). (3.2)

2. Из уравнения (3.2) очевидно, что давление в изохорном процессе изменяется прямопропорционально абсолютной температуре

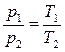. (3.3)

3. Графическое построение процесса

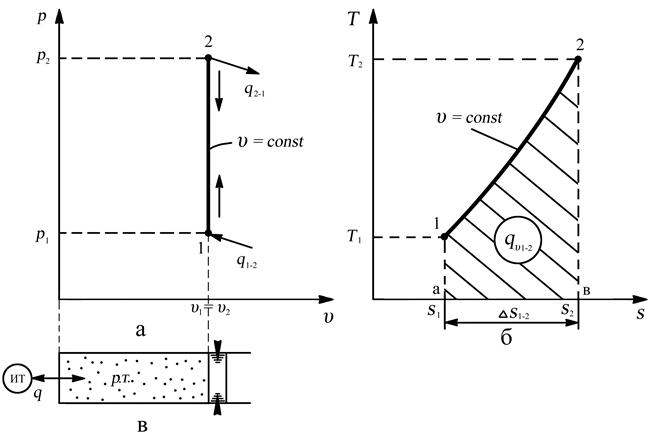
Рис. 3.1. Изохорный процесс: а – рабочая диаграмма процесса, б – тепловая диаграмма процесса, в – осуществление процесса

4. Определение величин входящих в первый закон термодинамики

а) q_υ = 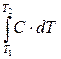= C_υ·(T₂ – T₁); (3.4)

б) ∆U_υ = = C_υ·(T₂ – T₁); (3.5)

в) L_υ = 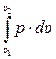= p·(υ₂– υ₁) = 0, (3.6)

т.к. υ₂= υ₁, т.е. газом в изохорном процессе работа не совершается.

Таким образом, в изохорном процессе согласно первому закону термодинамики вся теплота, подводимая к рабочему телу, расходуется только на увеличение внутренней энергии (увеличение температуры), при этом по уравнению (3.3) происходит увеличение давления. При отводе теплоты внутренняя энергия рабочего тела уменьшается, соответственно уменьшается и температура и давление. Поэтому для изохорного процесса первый закон термодинамики будет иметь следующий вид:

q_υ = ∆U_υ = C_υ·∆T . (3.7)

Используя графическое построение изохорного процесса в тепловой “T-s” диаграмме (рис. 3.1,б) определим количество теплоты q_υ1-2, участвующего в изохорном процессе. Площадь под линией изохорного процесса в тепловой “T-s” диаграмме даёт количество тепла q_υ1-2. Если кривизна линии 1–2 не очень значительна (что бывает, если изменение температуры невелико), то приближённо можно считать, что площадь под кривой 1–2 равна площади прямолинейной трапеции а12в:

пл. а12в = .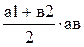

Заменяя длины отрезков а1 и в2 значениями температур, а отрезка ав – изменением энтропии, получим приближённую формулу для вычисления количества теплоты:

q_{υ 1-2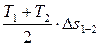} = (3.8)

или из первого закона термодинамики, и определения энтропии имеем:

q_{υ 1-2} = ∆U = T·∆s_1-2 . (3.9)

Знак количества теплоты определяется знаком изменения энтропии. Если ∆s_1-2 > 0, то это значит, что теплота подводится и q_{υ 1-2} > 0. Если ∆s_1-2 < 0, то теплота отводится и q_{υ 1-2} < 0.

г) Определим изменение энтропии, для изохорного процесса используя аналитическое выражение первого закона термодинамики (2.43)

dU = T·ds – p·dυ,

т.к. для изохорного процесса υ = const, и учитывая, что dυ = 0, dU = C_υ·dT имеем C_υ·dT = T·ds и получаем:

ds = C_υ· 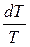. (3.10)

Чтобы найти изменение энтропии ∆s_1-2 при конечном изменении температуры T проинтегрируем выражение (3.10)

,

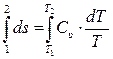при интегрировании считаем, что C_υ не зависит от T и окончательно получаем

∆s_1-2 = s₂ – s₁ = C_υ·ln 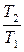= C_υ·ln 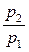= C_υ·2,3·lg 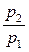. (3.11)

5. Распределение энергии в изохорном процессе изобразим в виде схем, представленных на рис. 3.2,а и 3.2,б. Коэффициент распределения энергии α = ∆U/q = 1.

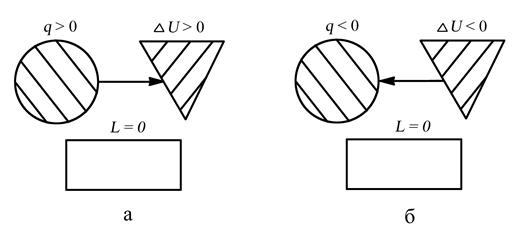
Рис. 3.2. Распределение энергии в изохорном процессе: а – при подводе теплоты к рабочему телу (процесс 1–2), б – при отводе теплоты от рабочего тела (процесс 2–1)

3.3. Изобарный процесс: определение, осуществление и исследование

Термодинамический процесс, протекающий при постоянном давлении рабочего тела, называется изобарным (от греческих слов изос – равный и барос – тяжесть).

Примером процесса, близкого к изобарному, является процесс подвода теплоты к рабочему телу в камерах сгорания авиационных ГТД.

3.3.1. Исследование изобарного процесса

1. Условие протекания процесса и есть уравнения процесса

p = const. (3.12)

Используя уравнение состояния идеального газа, получим уравнение изобарного процесса через параметры состояния

υ = 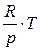= (const)·T или υ = f(T) . (3.13)

2. Из уравнения 3.13 очевидно, что удельный объём в изобарном процессе изменяется пропорционально абсолютной температуре

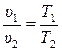. (3.14)

Если подводить теплоту к рабочему телу, его удельный объём (υ) и температура (Т) возрастают, а давление (р) останется неизменным (р = const). Физически это объясняется тем, что уменьшение числа молекул, приходящихся на единицу площади поверхности, вызванное ростом удельного объёма, компенсируется увеличением силы ударов каждой молекулы, обусловленным увеличением температуры (энергии) молекул.

3. Графическое построение процесса.

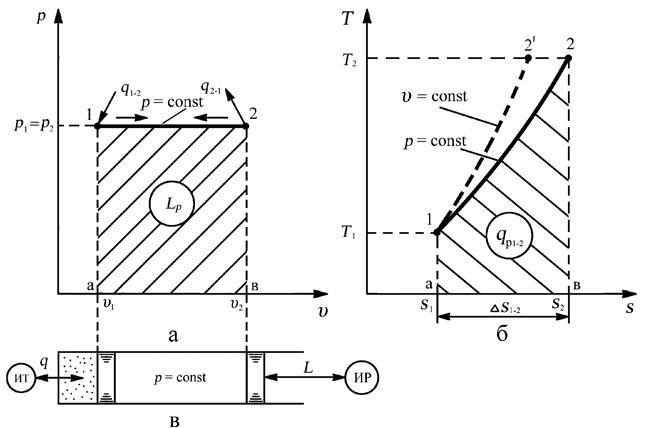
Рис. 3.3. Изобарный процесс: а – рабочая диаграмма процесса, б – тепловая диаграмма процесса, в – осуществление процесса

4. Определение величин входящих в первый закон термодинамики

а) q_p= 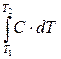= C_p·(T₂– T₁); (3.15)

б) ∆U_p= 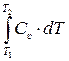= C_υ·(T₂– T₁); (3.16)

в) L_p= 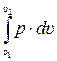= p·(υ₂– υ₁) = R·(T₂– T₁). (3.17)

Из формулы (3.17) видно, что работа расширения–сжатия совпадает с работой проталкивания. Следовательно, в открытой ТДС работа L расходуется на перемещение газа из области высокого в область низкого давления в процессе расширения. Такой процесс происходит в камере сгорания ГТД.

Таким образом, теплота, подводимая к рабочему телу в изобарном процессе, расходуется на увеличение внутренней энергии рабочего тела и совершения работы против внешних сил.

q_p = ∆U_p + L_p (3.18)

Теплота q_{p 1-2} , участвующая в изобарном процессе определяется из тепловой диаграммы (рис. 3.2,б). Площадь под линией процесса в тепловой “T-s” диаграмме даёт q_{p 1-2}

q_{p 1-2} = пл. а12в ≈ 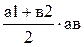= 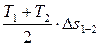. (3.19)

г) Определим изменение энтропии для изобарного процесса, используя аналитическое выражение первого закона термодинамики через энтальпию (2.44).

q_{p 1-2} = T·ds = di + υ·dp,

т.к. для изобарного процесса p = const и учитывая, что dp = 0, получаем:

q_{p 1-2} = T·ds = di = С_p·dT . (3.20)

Из уравнения (3.20) следует, что вся теплота, подведённая к рабочему телу, идёт на изменение энтальпии.

Проинтегрируем выражение (3.20) => 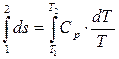и определим изменение энтропии ∆s_1-2 при конечном изменении температуры Т, при интегрировании считаем, что С_p не зависит от Т и окончательно получаем:

∆s_1-2 = s₂ – s₁ = C_p·ln 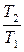= C_p·ln 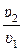= C_p·2,3·lg 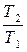. (3.21)

5. Распределение энергии, количественно оценивает коэффициент

α = 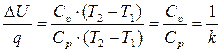. (3.22)

Для воздуха k = 1,41, поэтому из (3.22) имеем, что ∆U = 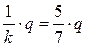. Это означает, согласно первому закону термодинамики, что из подведённого тепла q в изобарном процессе бόльшая часть ( 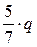) расходуется на изменение внутренней энергии рабочего тела, а меньшая часть ( 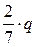) идёт на совершение работы против внешних сил (рис. 3.4,а и 3.4,б).

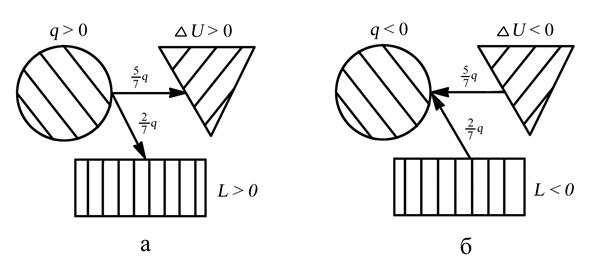
Рис. 3.4. Распределение энергии в изобарном процессе: а – при подводе теплоты к рабочему телу (процесс 1–2), б – при отводе теплоты от рабочего тела (процесс 2–1)

Из сравнения графиков изохорного и изобарного процессов в тепловой “T-s” диаграмме (рис. 3.3,б) можно заметить их внешнее сходство, поэтому важно уметь различать, каким образом эти две зависимости υ = const (линия 1–2') и p = const (линия 1–2) располагаются относительно друг друга при одинаковых начальных параметрах рабочего тела. Изохора в тепловой “T-s” диаграмме будет круче, чем изобара в тех же координатах по той причине, что подведённое тепло в изохорном процессе идёт только на увеличение внутренней энергии рабочего тела, естественно повышение температуры рабочего тела происходит более интенсивно, чем в изобарном процессе, в котором часть подведённого тепла идёт ещё на совершение работы.

3.4. Изотермический процесс: определение, осуществление, исследование

Термодинамический процесс, протекающий при постоянной температуре рабочего тела называется изотермическим (от греческих слов изос – равный, терме – тепло, жар). Примером изотермического процесса может служить процесс сжатия воздуха в компрессоре ГТД при условии, что в него производится впрыск легкоиспаряющейся жидкости. В компрессоре жидкость испаряется за счёт теплоты, выделившейся при сжатии воздуха. Тем самым обеспечивается постоянство температуры. Такой способ иногда используется для увеличения тяги (мощности) ГТД.

3.4.1. Исследование изотермического процесса

1. Условие протекания и есть уравнение процесса

T = const. (3.23)

Поскольку T = const, значит dT = 0, а dq ≠ 0, то теплоёмкость изотермического процесса равна: C_T = dq/dT = ± ∞.

Воспользовавшись условием протекания процесса и уравнением состояния идеального газа (p·υ = R·T), получим уравнение изотермического процесса через параметры состояния

p·υ = p₁·υ₁= p₂·υ₂=const . (3.24)

2. Из уравнения (3.24) очевидно, что давление в изотермическом процессе изменяется обратно пропорционально изменению удельного объёма

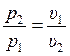. (3.25)

3. Графическое построение процесса.

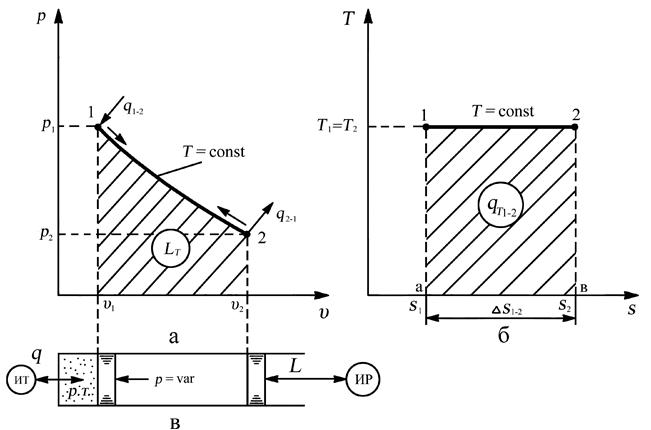
Рис. 3.5. Изотермический процесс: а – рабочая диаграмма процесса, б – тепловая диаграмма процесса, в – осуществление процесса

4. Определение величин входящих в первый закон термодинамики.

а) Сначала получим формулу для вычисления работы газа в изотермическом процессе. Для этого выразим текущее значение давления p через объём из уравнения процесса (3.24):

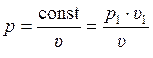; (3.26)

Далее проведя ряд преобразований, получим выражение для определения работы в изотермическом процессе:

L_Т = 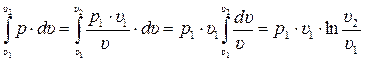(3.27)

или

L_Т = 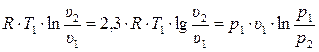(3.28)

б) В изотермическом процессе внутренняя энергия системы сохраняется неизменной, т.е. отсутствует изменение внутренней энергии

∆U_Т = 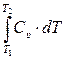= 0. (3.29)

в) Согласно первому закону термодинамики, количество теплоты определяется по формуле:

q_Т = ∆U_Т + L_Т, т.к. ∆U_Т = 0 и учитывая (3.28) получаем

q_Т = L_Т = 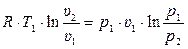(3.30)

Таким образом, в изотермическом процессе всё подведённое тепло расходуется на совершение работы против внешних сил. Теплоту q_Т в изотермическом процессе в координатах “T-s” определяют по площади прямоугольника а12в (рис. 3.5.)

пл. а12в = а1·ав или

q_Т = T·∆s_1-2.

г) Зная величину теплоты, участвующей в процессе всегда можно определить изменение энтропии для данного процесса по формуле

∆s_1-2 = 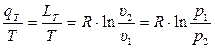. (3.31)

5. Распределение энергии в изотермическом процессе представлено на рис. 3.6., а коэффициент распределения энергии α = 0.

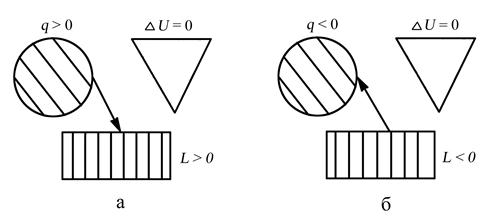
Рис. 3.6. Распределение энергии в изотермическом процессе: а – при расширении рабочего тела (процесс 1–2), б – при сжатии рабочего тела (процесс 2–1)

3.5. Адиабатный (изоэнтропический) процесс: определение,

осуществление, исследование

Адиабатным называется термодинамический процесс, в котором рабочее тело (система) не обменивается теплотой с окружающей средой.

Таким образом, характеристикой адиабатного процесса является условие q = 0 или s = const (ds = 0), которое должно соблюдаться в течение всего процесса. Поскольку dq = 0, а dT ≠ 0, то теплоёмкость адиабатного процесса C_ад = dq/dT = 0. Практически адиабатными могут считаться процессы, проходящие в хорошо изолированных от теплообмена устройствах, а также быстро протекающих процессах, что теплообмен, между газом (рабочим телом) и стенками окружающими газ, не успевает произойти. Газ (рабочее тело) при этом получает или теряет ничтожное количество теплоты.

Примером адиабатного процесса могут служить процессы сжатия воздуха во входном устройстве и компрессоре ГТД, процессы расширения газа в турбине и выходном устройстве ГТД при определённых допущениях. Необходимо пренебречь трением и предположить, что нет теплообмена через стенки корпусов элементов ГТД (идеальные входное устройство, компрессор, турбина, выходное устройство).

3.5.1. Исследование адиабатного процесса

1. Уравнение адиабатного процесса имеет вид:

p·υ^k = const, (3.32)

где k – показатель адиабаты.

Для того чтобы получить уравнение адиабатного процесса (3.32) воспользуемся уравнениями первого закона термодинамики (2.41 и 2.44) в дифференциальной форме:

dq = dU + p·dυ,

di = dq + υ·dp.

Перепишем данные уравнения в другом виде, используя известные соотношения и условия протекания процесса q = 0, т.е.

0 = С_υ·dT + p·dυ,

С_p·dT = 0 + υ·dp.

Далее преобразуя, получим:

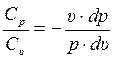
или

.

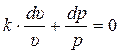Для решения этого дифференциального уравнения, проинтегрируем его считая, что C_p и C_υ остаются постоянными:

;

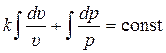k·lnυ + lnp = const, и окончательно получаем

p·υ^k = const, что и требовалось доказать.

2. Соотношение между параметрами в адиабатном процессе получаются из уравнения процесса (3.32)

p·υ^k = p₁· 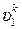= p₂· 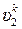= const . (3.33)

Это уравнение (3.33) даёт соотношение между давлениями и объёмами в адиабатном процессе

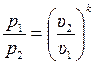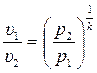; . (3.34)

Соотношение между температурами и объёмами получим из уравнения (3.34) путём его преобразования и использования уравнения состояния идеального газа (1.11)

p₁·υ₁· 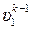= p₂·υ₂· 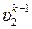(3.35)

R·T₁· 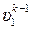= R·T₂· 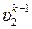. (3.36)

Из уравнения (3.36) находим соотношение между температурами и объёмами в начале и в конце адиабатного процесса:

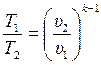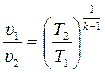; . (3.37)

Заменив в уравнении (3.37) отношение объёмов из уравнения (3.34) отношений давлений получим:

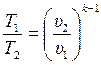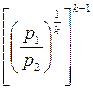= . (3.38)

И окончательно соотношение температур и давлений в адиабатном процессе будет иметь вид

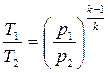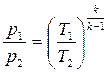; . (3.39)

Полученное выражение (3.34), (3.37), (3.39) дают нам соотношение между параметрами рабочего тела в начале и в конце адиабатного процесса.

Кроме полученных соотношений полезно определить соотношение между давлениями и плотностями, а также между температурами и плотностями рабочего тела, имея в виду, что плотность есть величина обратная удельному объёму.

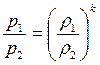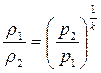; . (3.40)

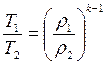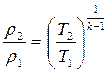; . (3.41)

3. Графическое построение процесса.

График процессов в “p-υ” координатах представляет собой неравнобокую гиперболу, а в координатах “T-s” будет представлять собой отрезок прямой, параллельной оси абсолютной температуры.

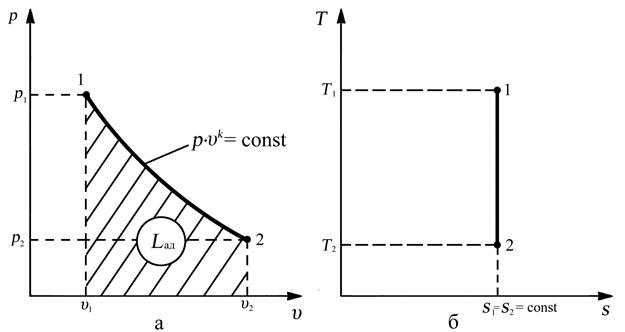
Рис. 3.7. Адиабатный процесс: а – рабочая диаграмма процесса,

б – тепловая диаграмма процесса

4. Определение величин входящих в первый закон термодинамики:

а) q_ад = 0 по условию протекания процесса;

б) ∆U_ад = C_υ·∆T = C_υ·(T₂ – T₁);

в) Работа газа в адиабатном процессе определяется по уравнению (2.15)

L_ад = 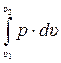, в котором текущее значение давления pопределено через объём по уравнению (3.33)

p = = .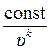

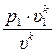Далее, проведя ряд преобразований, используя известные зависимости между параметрами, получим выражение для определения адиабатной работы газа

L_ад =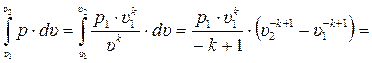

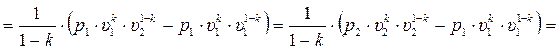
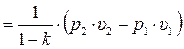. (3.42)

Используя уравнение состояния (1.11) получим выражение адиабатной работы через изменение температур:

L_ад = 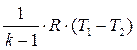. (3.43)

Из первого закона термодинамики имеем:

q_ад = ∆U_ад + L_ад, т.к. q_ад = 0 → L_ад = –∆U_ад.

Применив соотношение (2.11) и (2.30) получим:

L_ад = –∆U_ад = C_υ·(T₂ – T₁) = 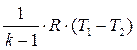. (3.44)

Преобразуем соотношение (3.44) воспользовавшись выражением (3.39), получим работу в адиабатном процессе расширения через изменение давлений

L_{ад. расш.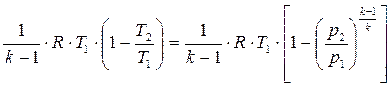} = . (3.45)

А адиабатная работа сжатия (по принятому правилу определения знаков работы) будет иметь следующий вид:

L_{ад. сж.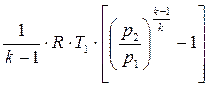} = . (3.46)

г) ∆s = 0, таким образом, в адиабатном процессе энтропия системы сохраняется неизменной.

5. Распределение энергии в адиабатном процессе определяет равенство:

L_ад = –∆U_ад.

Это равенство показывает, что в адиабатном процессе работа расширения (процесс 1–2) осуществляется за счёт уменьшения внутренней энергии рабочего тела, а работа сжатия (процесс 2–1) затрачивается на увеличение его внутренней энергии. Схема распределения энергии представлена на рис. 3.8.

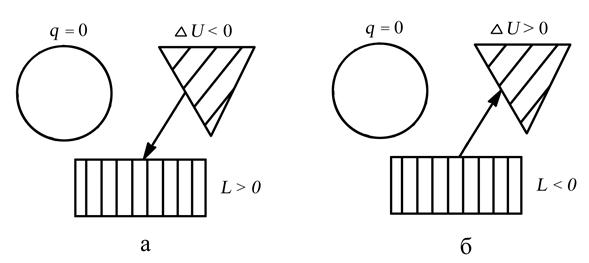
Рис. 3.8. Распределение энергии в адиабатном процессе: а – при расширении рабочего тела (процесс 1–2), б – при сжатии рабочего тела (процесс 2–1)

3.6. Сравнение адиабаты и изотермы

Сравнивая графики изотермического и адиабатного процессов можно заметить их внешнее сходство, поэтому важно уметь различать каким образом эти две зависимости (графики) располагаются относительно друг друга при одинаковых начальных параметрах рабочего тела.

Рассмотрим процесс расширения рабочего тела (рис. 3.9,а) из состояния 1 с параметрами p₁, υ₁ по изотерме 1–2 в состояние 2 с параметрами p₂, υ₂, и по адиабате 1–2' в состояние 2' с параметрами 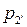, υ₂. Согласно уравнению изотермического расширения p = R·T/υ = const/υ, с увеличением удельного объёма υ рабочего тела происходит пропорциональное уменьшение его рабочего давления p. А при адиабатном расширении (p = R·T/υ) удельный объём υ увеличивается на ту же величину, что и в изотермическом процессе, но кроме этого происходит уменьшение температуры, т.к. в адиабатном процессе работа расширения осуществляется за счёт уменьшения внутренней энергии рабочего тела. Поэтому уменьшение давления в адиабатном процессе происходит более интенсивно, чем в изотермическом процессе. Следовательно, адиабата будет протекать более круче, чем изотерма, и в процессе расширения она располагается ниже изотермы (рис. 3.9,а). А в процессе сжатия адиабата располагается выше изотермы (рис. 3.9,б).

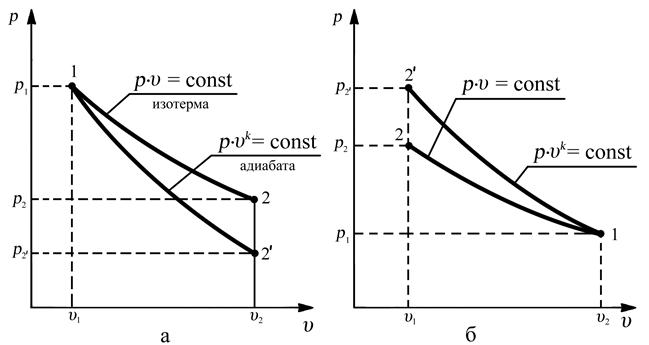
Рис. 3.9. Сравнение адиабаты и изотермы: а – процесс расширения газа,

б – процесс сжатия газа

3.7. Обобщающее значение политропных процессов

Реальные процессы в элементах авиационных двигателей протекают при наличии теплообмена и с изменением параметров рабочего тела (p, υ, T). Естественно реальные процессы не могут быть описаны ранее полученными закономерностями для основных термодинамических процессов. Поэтому используют другие процессы, более близкие к действительным термодинамическим процессам, протекающим в авиационных двигателях. Наиболее простым из них считают политропный процесс – это термодинамический процесс, при осуществлении которого может изменяться любой из параметров состояния (p, υ, T), а также возможен теплообмен с окружающей средой.

Примерами политропных процессов могут служить процессы сжатия и расширения рабочего тела в ГТД с учётом сил трения.

1. Уравнение процесса: p·υⁿ = const, где n показатель политропы. Показатель n может быть любым числом (–∞ < n < +∞), следовательно, политропных процессов бесконечное множество. Но в каждом конкретном процессе величина n постоянна.

2. Поскольку уравнение политропного процесса совпадает по форме с адиабатным, то легко можно получить соотношения между параметрами в начале и в конце политропного процесса, заменив в формулах (3.34), (3.37), (3.39) показатель адиабаты k на показатель политропы n.

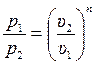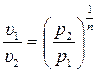; (3.47)

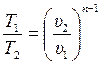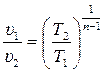; (3.48)

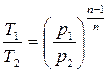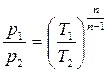; (3.49)

При исследовании реальных процессов необходимо бывает установить, является ли данный процесс политропным, а затем определяется показатель политропы n из уравнения (3.47) по значению параметров газа в каких–либо двух точках этого процесса.

lg 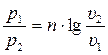, т.е. n = 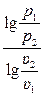. (3.50)

Для каждого из реальных необратимых процессов значения показателей политропы лежат в тех диапазонах, которые определяются расположением кривой реального процесса. Так в реальном компрессоре кривая процесса сжатия располагается между адиабатной (n = k) и изохорой (n = ± ∞) линия О…комп. (рис. 3.10.). Следовательно теоретически показатель политропы процесса сжатия в компрессоре n_комп. (k < n _комп. < ∞) ненамного превышает показатель адиабаты k.

Обработка показателей многих компрессоров показывает, что n_комп. = 1,46…1,47 > k_возд. = 1,41.

В реальной газовой турбине кривая процесса расширения линия О…турб. (рис. 3.10.) лежит между адиабатой (n = k) и изохорой (n = 1) и теоретически k < n_турб. < 1. Но практически, показатель политропы процесса расширения в турбине n_турб. гораздо ближе к показателю адиабаты и составляет

n_турб. = 1,27…1,29 < k_г для продуктов сгорания k_г = 1,33.

3. Определение величин, входящих в первый закон термодинамики

а) q_n = С_n·(T₂ – T₁), (3.51)

где С_n – теплоёмкость газа в политропном процессе.

б) –∆U = C_υ·(T₂ – T₁) (3.52)

в) L_n = 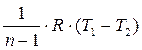. (3.53)

Это уравнение по форме одинаково с соответствующим уравнением для адиабатного процесса и отличается от него только значением показателя политропы n.

Найдём формулу для вычисления С_n в произвольном политропном процессе. Для этого подставим в уравнение первого закона термодинамики величины q_n, ∆U, L_n их аналитическое выражение. В результате получим:

q_n = ∆U + L_n

С_n·∆T = C_υ·∆T +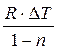

С_n = C_υ + 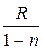или С_n = C_υ · 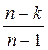. (3.54)

Из этого выражения видно, что если считать теплоёмкость C_υ не зависящей от температуры, то С_n для идеального газа в политропном процессе будет постоянна и её можно всегда найти, зная C_υ, R и n.

4. Каждому политропному процессу соответствует своё распределение энергии. Поскольку таких процессов множество, исследовать их все не представляется возможным. Однако качественное суждение о характере распределения энергии в любом политропном процессе можно сделать, рассмотрев его расположение по отношению к известным нам процессам: изохорному, изобарному, изотермическому и адиабатному (рис. 3.10.), которые являются частными случаями политропных процессов. Уравнение каждого из них можно представить в виде p·υⁿ = const со своим значением показателя политропы.

Действительно, при n = 0 уравнение политропы получает вид:

p·υ° = p·1 = const или p = const (изобарный процесс).

Изобарный процесс (n = 0) делит область политропных процессов на две части. Процессы, графики которых расположены выше изобары, происходят с увеличением давления, ниже изобары – с уменьшением давления.

При n = 1 уравнение политропы описывает изотермический процесс:

p·υ¹ = p·υ = const.

Изотермический процесс разделяет все процессы на две группы. Политропы, расположенные выше изотермы соответствуют процессам, которые сопровождаются увеличением внутренней энергии (повышением температуры), ниже изотермы – уменьшением внутренней энергии (понижением температуры).

При n = k, политропы совпадают с адиабатой:

p·υ^k = const.

Адиабатный процесс (n = k) делит все политропные процессы на две группы. Если политропа расположена выше адиабаты, ей соответствует процесс, который протекает с подводом теплоты (q > 0) к рабочему телу, а если ниже адиабаты, то с отводом теплоты (q < 0) от рабочего тела.

При n = ± ∞ (при очень больших абсолютных значениях n) уравнение политропы преобразуется в уравнение изохоры, извлекая корень степени n из уравнения политропы, получим:

.

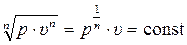При n → ± ∞ величина 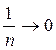, , 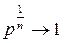следовательно, при n = ± ∞ получаем υ = const.

Изохорный процесс (n = ± ∞) разделяет всю область политропных процессов на две части. Политропы, расположенные справа от изохоры, соответствуют процессам, которые осуществляются с увеличением объёма, следовательно, газом совершается при этом работа расширения против внешних сил (L > 0). Если политропы расположены слева от изохоры, то такой процесс происходит с уменьшением объёма. При этом внешние силы совершают над газом работу (L < 0), сжимая его.

Таким образом, если известны показатель политропы и характер или график процесса, то можно определить при каких условиях он может осуществляться: с подводом или отводом теплоты, с увеличением или уменьшением внутренней энергии, совершением механической работы рабочим телом или внешними силами над рабочим телом.

Покажем области политропных процессов в зависимости от показателя политропы в координатах “p-υ” и “T-s”.

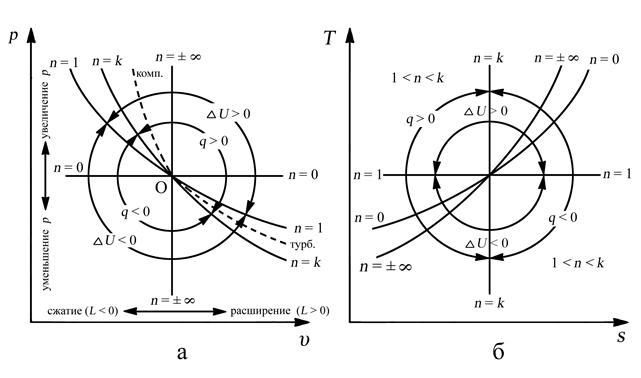
Рис. 3.10. Области политропных процессов: а – в “p-υ” координатах,

б – в “T-s” координатах

3.8. Энтальпийная “i-s” диаграмма (“i-s” координаты)

Недостатком диаграмм, построенных в “T-s” координатах, является необходимость вычислять площади отдельных участков диаграммы при определении теплоты q и работы L процесса, изменения внутренней энергии ∆u и энтальпии ∆i газа. Этого недостатка лишены диаграммы состояния, построенные в “i-s” координатах (энтальпия – энтропия), где величины q, L, ∆u, ∆i определяются по отрезкам прямых. Данная особенность “i-s” координат упрощает анализ и расчёт термодинамических процессов.

Рассмотрим протекание основных процессов с идеальными газами в “i-s” координатах (рис. 3.11.).

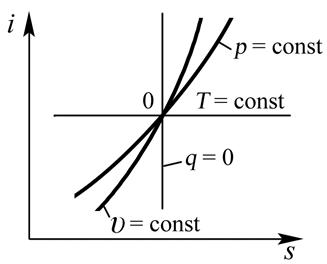Рис. 3.11. Изображение основных термодинамических процессов

в “i-s” координатах

Обратимый адиабатный процесс изображается в “i-s” координатах, как и в “T-s” координатах, прямой вертикальной линией (s = const).

Изотермический процесс. Для идеального газа

di = c_p·dT, (3.35)

поэтому

.

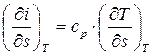Поскольку в изотермическом процессе 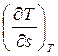= 0, то в случае идеального газа 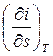= 0. Следовательно, изотерма идеального газа в “i-s” координатах представляет собой горизонтальную прямую.

Изобарный процесс. Здесъ

dq = T·ds = c_p·dT = di.(3.56)

Изобара представляет собой кривую линию, тангенс угла накло­на касательной к которой равен:

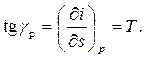(3.57)

Так как в изобарном процессе с ростом энтальпии увеличивается температура газа Т,то возрастает и γ_р. Следовательно изобара обращена выпуклостью к оси абс­цисс.

Изохорный процесс. По аналогии с изобарным процессом можно записать

dq = T·ds = c_υ·dT = 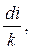(3.58)

отсюда

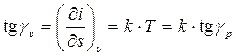. (3.57)

Следовательно, изохора так же, как и изобара, представляет со­бой кривую линию, обращенную выпуклостью к оси абсцисс. Взаимное расположение изобары и изохоры в “i-s” координатах (рис. 3.11.) аналогично с их расположением в “T-s” координатах.

С помощью “i-s” диаграммы нетрудно определить основные термодинамические величины. Зная положение точек начала 1 и конца 2процесса, непосредственно из диаграммы определяют­ся параметры газа в этих точках p₁, T₁, υ₁, p₂, T₂, υ₂ и величины

∆i = i₂ – i₁ и ∆s = s₂ – s₁ .

Изменение внутренней энергии найдется по формуле

∆u = ∆i – (p₂·υ₂ – p₁·υ₁).

Величины теплоты и работы зависят от типа процесса и опре­деляются следующим образом:

- в изобарном процессе q = ∆i, L = q –∆u;

- в изохорном працессе q = ∆u;

- в изотермическом процессе q = T·∆s, L = q;

- в адиабатном процессе L = ∆u.

Особое значение “i-s” диаграммы имеют в расчётах термодина­мических процессов с реальными газами, у которых сильно ме­няются теплоёмкость и другие свойства, что затрудняет исполь­зование аналитических формул.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 3.1.

Баллон с азотом ёмкостью 40 литров вносят с улицы, где температура –30 °С, в помещение с температурой +20 °С. Какое будет давление в баллоне и сколько азот воспримет теплоты, если его температура сравняется с температурой помещения? Первоначальное давление в баллоне 98·10⁵ Па. Теплоёмкость азота считать постоянной и равной C_υ = 742 Дж/(кг·К).

Решение

При нагревании баллона его объём практически не изменится (υ = const), следовательно, происходит изохорный процесс, применяя формулу (3.3) определим давление в баллоне при температуре 20 °С:

p₂ = p₁· 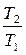= 98·10⁵· 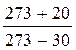= 118·10⁵ Па.

Проверим правильность получения размерности давления

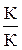Па· = Па.

По уравнению состояния (1.10) найдём массу азота в баллоне, имея в виду, что 1 литр = 10^-3 м³:

m = 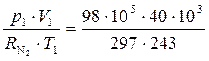= 5,43 кг,

где 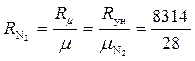= 297 Дж/(кг·К) – газовая постоянная азота (смотриформулу 1.14), или её значение может быть взято из справочных таблиц.

Проверим правильность получения размерности газовой постоянной и массы азота.

Универсальная газовая постоянная по величине одинаковая для всех газов и имеет следующую величину и размерность R_ун = 8 314 Дж/(кмоль·К), а масса одного киломоля азота – 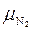= 28 кг/кмоль. Таким образом, размерность газовой постоянной азота будет следующая:

,

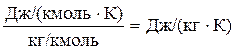а размерность массы азота:

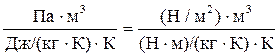= кг.

Теперь определим теплоту, воспринимаемую азотом при его нагреве от –30 °С до +20 °С:

Q = m·C_υ·(T₂ – T₁) = 5,43·742· (293 – 243) = 201,45 кДж.

Размерность теплоты, воспринимаемой азотом будет следующая:

.

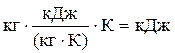Задача 3.2.

Воздух сжимается в поршневом компрессоре от 1·10⁵ Па до 7·10⁵ Па. Начальная температура воздуха 300 К, объём цилиндра 1,5 литра. Как изменяется температура и объём воздуха, если сжатие производится: а) по адиабате; б) по изотерме; в) по политропе с показателем политропы n = 1,2?

Решение

а) Адиабатное сжатие.

Показатель адиабаты для воздуха определяется по формуле (2.28) или может быть взят из справочных таблиц:

k = ;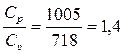

Используя зависимости (3.34), (3.39) между параметрами в адиабатном процессе находим искомые значения объёма и температуры воздуха в конце адиабатного сжатия:

V₂ = V₁· 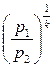= 1,5·10^-3· 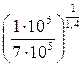= 0,376·10^-3 м³ = 0,376 литра;

T₂ = T₁· 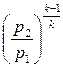= 300· 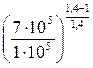= 528 К.

б) Изотермическое сжатие.

Температура в конце процесса сжатия равна температуре в начале процесса по условию протекания изотермического процесса, поэтому:

T₂ = T₁ = 300 К.

Объём в конце процесса сжатия определяется из уравнения (3.25):

V₂ = V₁· 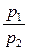= 1,5·10^-3· 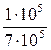= 0,214·10^-3 м³ = 0,214 литра.

в) Политропное сжатие.

Искомые параметры воздуха в конце политропного процесса сжатия находим по формулам (3.49) и (3.47):

T₂ = T₁· 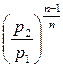= 300· 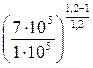= 416 К;

V₂ = V₁· 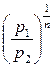= 1,5·10^-3· 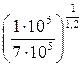= 0,297·10^-3 м³ = 0,297 литра.

Задача 3.3.

Один килограмм воздуха сжимается адиабатно от начальной температуры t₁ = 20 °C и давления p₁ = 2·10⁵ Па до давления p₂ = 16·10⁵ Па. Определить температуру в конце сжатия, конечный объём и работу, затраченную на сжатие. Для воздуха принять: k = 1,4; R = 287 Дж/(кг·К).

Решение

Из соотношения параметров в адиабатном процессе (3.39) определим температуру в конце процесса сжатия:

T₂ = T₁· 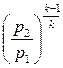= 293· 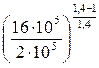= 532 К.

Из уравнения состояния (1.11) находим конечный объём одного килограмма (υ₂) воздуха:

υ₂ = 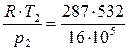= 0,095 м³/кг.

Работу, затраченную на сжатие воздуха находим по формуле (3.43):

L_{ад. сж.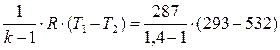} = = – 171 482 Дж/кг.

Знак минус в полученном результате означает, что адиабатная работа сжатия воздуха совершена внешними силами над воздухом.

Задача 3.4.

Определить показатель политропы процесса сжатия азота, если давление повышается от 1·10⁵ Па до 8·10⁵ Па, а температура от 293 до 450 К. Значение газовой постоянной азота определено в задаче 3.1.

Решение

Удельные объёмы азота в начале и в конце процесса сжатия находим по уравнению состояния (1.11):

υ₁ = 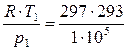= 0,87 м³/кг;

υ₂ = 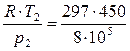= 0,167 м³/кг.

Значение показателя политропы определяется из соотношения (3.50)

n =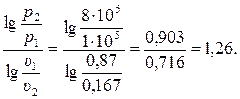

Проверьте, как Вы усвоили материал

1. В какой последовательности производится анализ термодинамических процессов?

2. В каком термодинамическом процессе вся подведённая теплота расходуется на изменение внутренней энергии?

3. Подводится или отводится теплота в процессе изобарного сжатия?

4. Чему равно изменение внутренней энергии при изотермическом процессе.

5. Как изменяется температура рабочего тела при расширении?

6. Чем отличается линия изобарного процесса от линии изохорного процесса в тепловой “T-s” диаграмме?

7. При каких условиях термодинамический процесс будет адиабатным?

8. Назовите термодинамический процесс, в котором всё подведённое тепло расходуется на совершение работы против внешних сил.

9. Чему равно изменение энтропии при адиабатном процессе?

10. Назовите термодинамический процесс, в котором рабочее тело совершает против внешних сил за счёт уменьшения своей внутренней энергии?

11. Как найти количество теплоты при графическом изображении процесса?

12. Как взаимно расположены адиабата и изотерма, в “p-υ” и “T-s” координатах?

13. В каком термодинамическом процессе вся теплота, подведённая к рабочему телу, идёт на увеличение энтальпии?

14. Изобразите основные идеальные термодинамические процессы в диаграммах состояния, построенных в “i-s” координатах.

Дата добавления: 2014-09-08; просмотров: 3526; Нарушение авторских прав

Мы поможем в написании ваших работ!