
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ТЕМА 4. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
4.1. Понятие о круговых процессах (циклах).
Прямой цикл (цикл тепловой машины)
В предыдущих темах были рассмотрены так называемые разомкнутые термодинамические процессы. Поскольку в них некоторые параметры рабочего тела непрерывно и односторонне изменяются, что такие процессы неизбежно заканчиваются при каких-то конечных значениях давления и температуры. Осуществляя их можно получить лишь ограниченную величину работы. Бесконечное непрерывное расширение заданной массы рабочего тела практически получить невозможно. Следовательно, для непрерывного получения полезной работы необходимо осуществлять периодически повторяющийся процесс расширения. Повторение же процесса расширения можно обеспечить, если возвращать рабочее тело в начальное состояние после завершения его расширения, т.е. совершать периодически повторяющиеся термодинамические процессы.
Совокупность термодинамических процессов, в результате которых рабочее тело возвращается в первоначальное состояние, называется круговым процессом или циклом.
Циклы имеют большое практическое значение, так как они позволяют осуществлять превращение теплоты в работу, а также непрерывную передачу теплоты с низшего температурного уровня на высший.
Рассмотрим круговой процесс (цикл) теплового двигателя.
Тепловой двигатель представляет собой механическое устройство, в котором теплота непрерывно превращается в полезную работу. Циклы тепловых двигателей протекают по часовой стрелке, и они называются прямыми циклами.
Перейдём к рассмотрению кругового процесса теплового двигателя (рис. 4.1.).
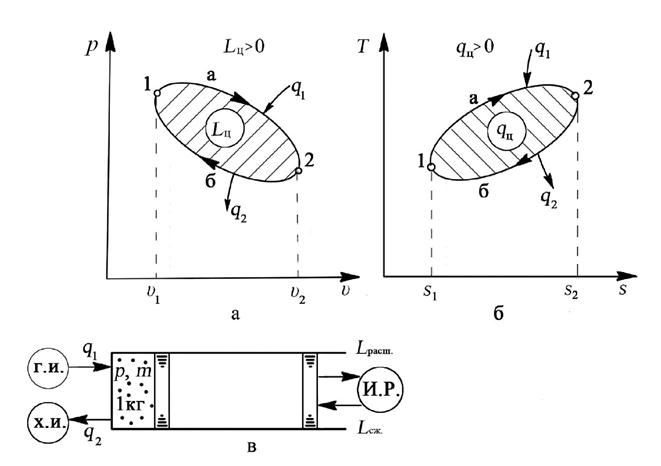
Рис. 4.1. Круговой процесс (цикл) теплового двигателя: а – изображение прямого цикла в рабочей диаграмме, б – изображение прямого цикла в тепловой диаграмме, в – осуществление кругового процесса
Возьмём цилиндр с поршнем, который может передвигаться без трения. Поместим в цилиндр 1кг идеального газа, имеющего некоторое избыточное давление. Если подвести к газу теплоту, он начнет расширяться и при этом совершать положительную работу до тех пор, пока давление газа не станет равным внешнему давлению.
Работа расширения Lрасш полученная при этом, в координатах “p-υ”изобразится (рис. 4.1,а) площадью υ11a2υ2. Чтобы осуществить вновь процесс расширения, необходимо возвратить рабочее тело в начальное состояние путем его сжатия.
Если процесс сжатия будет происходить при той же температуре, что и процесс расширения (по линии 2а1), работа сжатия будет в точности равна работе расширения и никакой избыточной (полезной) работы такой двигатель вырабатывать не будет.
Поэтому для получения полезной работы в тепловом двигателе, работа сжатия должна быть меньше работы расширения. Этого можно достигнуть, если температура рабочего тела, при сжатии будет более низкая, чем при его расширении. При этом рабочее тело создает меньшее сопротивление силам, сжимающим его, поэтому на сжатие рабочего тела, необходимого для возвращения в начальное состояние, при более низкой температуре требуется меньше работы.
Таким образом, при сжатии, от рабочего тела необходимо отводить теплоту, чтобы понизить его температуру T и соответственно понижается давление p рабочего тела.
Работа сжатия Lсж в координатах “p-υ” изображается площадью υ22б1υ1. Из (рис. 4.1,а) видно, что площадь υ11a2υ2 больше площади υ22б1υ1, т.е. Lрасш > Lсж.
4.2. Полезная работа цикла. Термический КПД цикла
Разность работ расширения и сжатия называется полезной работой цикла Lц:
Lц = Lрасш – Lсж . (4.1)
Работа цикла в координатах “p-υ ”изображается площадью, описываемой круговым процессом 1-а-2-б-1.
Из приведенного анализа цикла следует, что для получения полезной работы в круговом процессе необходимо иметь:
- горячий источник (теплоотдатчик), отдающий рабочему телу теплоту при его расширении;
- рабочее тело, которое совершает работу при расширении;
- холодный источник (холодильник), который воспринимает теплоту от рабочего тела, при его сжатии (рис. 4.1,в).
Связь между теплотой, подведённой к рабочему телу q1 и отведённого от него q2 и работой цикла Lц можно установить, применив первый закон термодинамики к процессам, составляющим цикл:
- для процесса расширения q1 = ΔU12 + Lрасш;
- для процесса сжатия –q2 = –ΔU21 – Lсж.
Суммируя эти уравнения и учитывая, что ΔU12 = –ΔU21, получим:
q1 – |q2| = Lрасш – Lсж = Lц . (4.2)
Таким образом, полезная работа цикла пропорциональна разности подведённой к рабочему телу и отведённой от него теплоты. То есть количество работы, совершённой термодинамической системой за цикл, должно равняться количеству теплоту полученной системой в течение того же цикла. Можно говорить, что в рассмотренном круговом процессе произошло превращение теплоты qц = q1 – |q2| в механическую работу Lц.
qц = Lц = q1 – |q2| (4.3)
Рассмотренный цикл совершается в тепловых двигателях, а сам цикл называется термодинамическим циклом или просто циклом тепловых двигателей.
На рис. 4.2. изображена схема, отображающая принципиальные условия работы теплового двигателя:
 |
Рис. 4.2. Принципиальная схема работы теплового двигателя
Термодинамическая система, обеспечивающая циклическое действие теплового двигателя в течение необходимого достаточно продолжительного времени, должна включать:
- рабочее тело (газ или пар), получающее теплоту и переводящее её в работу цикла Lц;
- теплоотдатчик (горячий источник тепла), сообщающий за цикл каждой единице массы рабочего тела теплоту q1.
Теплоприемник (холодный источник тепла), куда от единицы массы рабочего тела отводится за цикл теплота q2.
Очевидно, что для получения положительной работы цикла должно быть q1 > q2. Следовательно, в тепловом двигателе только часть теплоты, получаемой от теплоотдатчика (от горячего источника), преобразуется в полезную работу.
А теплота q2, поступающая в теплообменник (холодильник), утрачивает свою ценность как энергия, которая может быть преобразована в работу.
Степень преобразования теплоты в работу в тепловом двигателе оценивается термическим КПД.
Термическим КПД цикла ηt называется отношение тепла, превращённого в работу цикла, ко всему подведенному за цикл теплу:
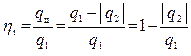 (4.4)
(4.4)
Термический КПД цикла характеризует совершенство цикла теплового двигателя с точки зрения преобразования, в полезную работу подведённого к рабочему телу тепла.
Значение КПД цикла зависит от условий, в которых происходит подвод и отвод теплоты, а также от характера (типа) термодинамических процессов, из которых составлен конкретный цикл. При прочих равных условиях наибольшее значение термического КПД будет иметь такие циклы, в которых все процессы являются равновесными (обратимыми).
Цикл являются обратимым, если он состоит только из обратимых термодинамических процессов. Если хотя бы один термодинамический процесс в цикле является, необратимым, цикл также будет необратимым. Процессы, протекающие в реальных технических устройствах, необратимы. Следовательно, необратимы все циклы реализуемые в тепловых машинах.
Согласно формуле (4.4) для всех тепловых двигателей, в том числе и идеальных всегда ηt < 1.
4.3. Цикл Карно и теорема Карно
Сочетая различные термодинамические процессы, можно получить множество циклов, каждому из которых будет соответствовать определённое значение термического КПД ηt. Возникает естественный вопрос, какой же цикл будет иметь ηt = ηt max.
При исследовании проблемы повышения КПД тепловых машин, Сади Карно в 1824 году был предложен идеальный обратимый цикл, носящий в настоящее время его имя.
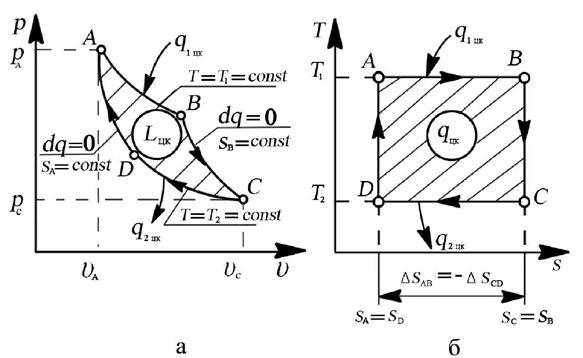 На рис. 4.3. показан идеальный обратимый цикл Карно в рабочей и тепловой диаграммах.
На рис. 4.3. показан идеальный обратимый цикл Карно в рабочей и тепловой диаграммах.
Рис. 4.3. Цикл Карно: а – изображение цикла Карно в рабочей “p-υ” диаграмме,
б – изображение цикла Карно в тепловой “T-s” диаграмме
Процессы, составляющие этот цикл, протекают следующим образом. Пусть теплоотдатчик имеет постоянную температуру T1, а теплоприемник – постоянную температуру T2 < T1.
Считаем, что их размеры настолько велики, что подвод теплоты q1 цк к рабочему телу и отвод от него теплоты q2 цк на величину T1 и T2 не влияют. Рабочим телом является идеальный газ.
От исходного состояния А (рис. 4.3,а) рабочее тело расширяется изотермически (T1 = const) до состояния В, получая от теплоотдатчика теплоту q1 цк. Дальнейшее расширение происходит адиабатным процессом ВС до тех пор, пока температура рабочего тела не снизится до величины T2. Для возвращения рабочего тела в исходное состояние осуществляется его сжатие в изотермическом процессе CD (T2 = const). При этом в теплоприемник отводится теплота q2 цк. Цикл замыкается адиабатным процессом сжатия DA,в котором рабочее тело возвращается в исходное состояние A с температурой T1. Таким образом, цикл Карно состоит из двух изотермических и двух адиабатных процессов.
Заметим, что поскольку цикл обратим, то изотермические процессы подвода и отвода тепла должны происходить при бесконечно малой разнице между температурами теплоотдатчика (или теплоприемника) и рабочего тела. Это позволяет считать, что в процессе изотермического расширения температура рабочего тела равна температуре теплоотдатчика T1, а в процессе изотермического сжатия – температуре теплоприемника T2.
На рис. 4.3,б цикл Карно представлен в тепловой “T-s” диаграмме:
1. В “T-s” диаграмме изотермический процесс подвода тепла к системе изображается линией AB, параллельной оси абсцисс. В этом процессе рабочее тело получает теплоту q1 цк > 0, в результате чего его энтропия возрастает от sA до sB на величину:
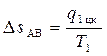 . (4.5)
. (4.5)
2. Далее следует адиабатное расширение по линии BC, в ходе которого температура рабочего тела уменьшится от T1 до T2, и при этом энтропия рабочего тела остаётся неизменной sB = sС.
3. При температуре T2 происходит изотермический процесс сжатия по линии CD, в ходе которого рабочее тело отдает приёмнику теплоту в таком количестве q2 цк, чтобы энтропия рабочего тела от значения sB = sС, снова вернулась к значению sA = sD,
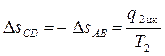 . (4.6)
. (4.6)
4. Цикл завершается адиабатным сжатием DA, в ходе которого температура повышается от T2 до T1, принимая, таким образом, первоначальное значение.
Теперь легко определить КПД цикла Карно, т.е. КПД идеального теплового двигателя. В уравнение (4.4) подставим значения количеств теплоты q1 цк и q2 цк из (4.5 и 4.6), выраженных через температуры и изменения энтропии в процессах AB и CD:
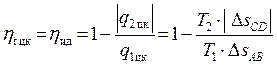 .
.
Так как ΔsAB = |ΔsCD|, имеем, что:
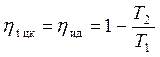 . (4.7)
. (4.7)
Из полученного выражения (4.7) видно, что термический КПД цикла Карно зависит только от температур источника (T1) и приёмника (T2) теплоты. Никакие физические свойства рабочего тела не вошли в выражение для ηt цк. Эти выводы составляют содержание так называемой теоремы Карно, которая формулируется следующим образом: Термический КПД цикла Карно зависит только от температур теплоотдатчика (T1) и теплоприёмника (T2) и не зависит от свойств рабочего тела.
Из анализа формулы (4.7) следует:
1. Чем выше T1 и чем ниже T2, тем выше ηt цк.
Хотя в настоящее время имеется техническая возможность получения очень высоких температур (сотни тысяч градусов), однако в реальных двигателях использовать эти температуры практически не представляются возможным, так как материалы, из которых изготовлены детали двигателей, не способны выдерживать такие температуры. Максимальная температура (T1), практически реализуется в большинстве двигателей, близка к 1000…2000 К. Имеются двигатели (например, ракетные), в которых используются более высокие температуры до 4000 К. Однако эти двигатели рассчитаны на очень короткий срок службы (не более нескольких десятков минут).
Что касается температуры T2, то она приблизительно составляет 300 К, поскольку приёмником теплоты для всех двигателей, работающих в наземных условиях, является либо атмосферный воздух, либо вода в водоемах, реках, морях.
Вообще говоря, искусственно может быть получена температура, даже близкая к нулю, однако получение температур ниже температуры окружающей среды связанно с затратой работы. Затрата работы оказывается больше, чем выигрыш в КПД, поэтому такой путь увеличения КПД оказывается неприемлемым.
2. Эффективность превращения теплоты в работу (термический КПД) в любом цикле не может быть больше, чем в цикле Карно, осуществляемом в том же интервале температур.
3. Термический КПД цикла Карно всегда меньше единицы, так как не существует источников теплоты с бесконечно высокой температурой (T1 = 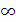 ) или же приемников теплоты (T2 = 0), то соотношение T2/T1 всегда больше нуля. Следовательно, КПД цикла Карно, а тем более любого другого цикла всегда меньше единицы.
) или же приемников теплоты (T2 = 0), то соотношение T2/T1 всегда больше нуля. Следовательно, КПД цикла Карно, а тем более любого другого цикла всегда меньше единицы.
4. Когда T1 = T2, термический КПД цикла ηt цк = 0, следовательно, если все тела термодинамической системы имеют одинаковую температуру, т.е. находится в тепловом равновесии, то преобразование теплоты в работу невозможно.
Хотя теоретически цикл Карно является наиболее экономичным циклом, он не нашел практической реализации в тепловых машинах, использующих в качестве рабочего тела различные газы.
Цикл Карно с газообразным рабочим телом осуществлять нельзя, т.к. обеспечить изотермическое сжатие с непрерывным отводом теплоты в изотермическом компрессоре и изотермическое расширение с непрерывном подводом теплоты в изотермической турбине. Только в паросиловых установках отвод теплоты и иногда частично подвод теплоты происходят при постоянных температурах в процессах конденсации пара и при парообразовании.
В тепловом двигателе, работающему по циклу Карно и развивающему необходимую для практических целей мощность, диапазон изменения давления и объёма рабочего тела должен быть настолько большим, что двигатель получился бы недопустимо громоздким и тяжелым.
Смысл рассмотрения цикла Карно заключается в том, что его энергетические показатели Lцк и ηt цк являются предельно высокими по сравнению с любимыми другими циклами тепловых машин в заданном интервале температур максимальной T1 = Tг и минимальной T2 = Tн.
Поэтому показатели цикла Карно являются общим критерием оценки энергетической эффективности тепловых установок, в том числе ГТД и ДВС.
Таким образом, цикл Карно является базовым для оценки совершенства любого произвольного цикла, в том числе и цикла авиационного ГТД.
4.4. Обратные циклы (циклы холодильных машин)
Последовательность процессов в цикле может быть такая, что расширение рабочего тела термодинамической системы происходит при более низком давлении, чем сжатие (рис. 4.4,а)
Направление протекания этих процессов происходит против часовой стрелки, и они называются обратными циклами.
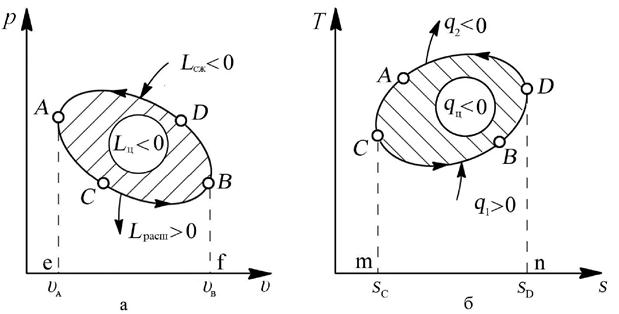
Рис. 4.4. Обратный цикл: а – изображение цикла холодильной машины (обратного цикла) в рабочей диаграмме, б – изображение цикла холодильной машины (обратного цикла) в тепловой диаграмме
В этом случае работа на участке BDA (Lсж = пл.eADBf) будет отрицательна, а на участке ACB (Lрасш = пл.eACBf) – положительна. Так как пл.eADBf > пл.eACBf, то работа за цикл будет отрицательна (Lц < 0):
Lц = Lрасш – | Lсж| = пл.eACBf - пл.eADBf < 0.
В соответствии с уравнением первого закона термодинамики qц = Lц, т.к. ΔUц = 0, поэтому теплота этого цикла также должна быть отрицательной: qц < 0.
Для этого необходимо, чтобы теплота подводилась к термодинамической системе при низкой температуре (линия CBD на рис. 4.4,б), а отводилась – при более высокой температуре (линия DAC). В этом случае:
qц = q1 – | q2 | = пл.mCBDn – пл.mCADn = пл.CBDAC < 0.
Обратим внимание на то, что при осуществлении такого цикла (в какой-либо машине) в процессе СBD рабочее тело машины отбирает теплоту в количестве q1 от холодного тела в окружающей среде, а в процессе DAC отдает теплоту в количестве q2 другому телу в окружающей среде, имеющему более высокую температуру, чем первое тело. Таким способом осуществляется передача теплоты с низшего температурного уровня на высший, т.е. производится охлаждение некоторых тел окружающей среды. Это охлаждение обязательно сопровождается превращением работы Lц, подведённой к машине, в теплоту qц. Одновременно с охлаждением одних тел в окружающей среде обязательно происходит нагревание других тел, которые получают как теплоту, взятую у холодного тела, так и теплоту, в которую превратилась работа цикла:
| q2 | = q1 – | qц | = q1 – | Lц | (4.8)
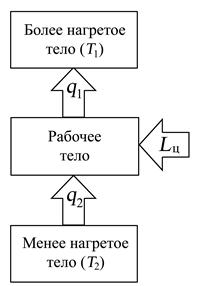 Таким образом, для осуществления обратного цикла (цикла холодильных машин) необходимо затратить механическую работу кого-либо постороннего источника работы. На рис. 4.5. изображена схема, отображающая принципиальные условия работы холодильной машины.
Таким образом, для осуществления обратного цикла (цикла холодильных машин) необходимо затратить механическую работу кого-либо постороннего источника работы. На рис. 4.5. изображена схема, отображающая принципиальные условия работы холодильной машины.
Рис. 4.5. Принципиальная схема работы холодильной машины
Холодильные установки (холодильные машины, просто холодильники) – это тепловые машины, служащие для отвода внутренней энергии от охлаждаемого тела, температура которой ниже температуры окружающей среды.
Холодильные установки используются для получения температуры от -10 °С до 15 °С.
Характеристикой холодильной установки является его холодильный коэффициент (ε), равный отношению количества теплоты отнятого от охлаждаемого тела q2 к затраченной работе цикла Lц (эта работа внешнего источника работы). Поэтому холодильный коэффициент для 1кг холодильного агента (рабочее тело), участвующего в цикле определяется следующей формулой:
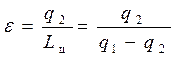 . (4.9)
. (4.9)
Если осуществляется обратный цикл Карно (идеальная холодильная машина) в интервале температур T1…T2, в ходе которого отбирается от холодного источника теплота q2 и передается источнику (окружающей среде) теплота q1, то на основании (4.5) и (4.6) имеем:
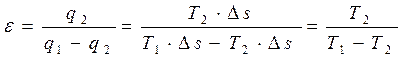 . (4.10)
. (4.10)
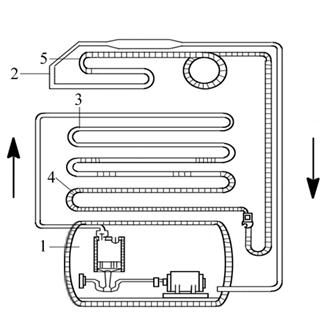 В качестве примера осуществления обратного цикла (цикла холодильной машины) познакомимся с работой бытового (компрессионного) холодильника. Компрессионная холодильная машина состоит из компрессора 1, испарителя 2 и конденсатора 3, заполненных хладагентом (рис. 4.6.).
В качестве примера осуществления обратного цикла (цикла холодильной машины) познакомимся с работой бытового (компрессионного) холодильника. Компрессионная холодильная машина состоит из компрессора 1, испарителя 2 и конденсатора 3, заполненных хладагентом (рис. 4.6.).
Рис. 4.6. Схема компрессионной холодильной машины
В качестве хладагента обычно применяется фреон – 12 (CF2CL2) – дифтордихлорметан. Он взыровобезопасен, не имеет запаха и обладает низкой температурой кипения (-29 °С при атмосферном давлении).
При работе компрессора, приводимого в действие электродвигателем, происходит отсасывание паров фреона из испарителя 2. Из-за пониженного давления процесс испарения ускоряется. Пары фреона сжимаются компрессором, при этом их температура повышается. В конденсаторе-теплообменнике 3, расположенном на задней стенке холодильника, пары фреона охлаждаются до комнатной температуры, отдавая некоторое количество теплоты окружающей среде, и конденсируются при постоянном давлении p1.
После прохождения фреона по капиллярным трубкам 4, 5, в испарителе давление снижается от p1 до p2. Жидкий фреон при понижении давления испаряется, его температура, и температура стенок испарителя понижаются. Такая циркуляция фреона происходит непрерывно, пока работает компрессор.
В конденсаторе холодильника выделяется количество теплоты q1 = q2 + Lц, где Lц – работа, совершённая электродвигателем компрессора, q2 – количество теплоты, отнятое у среды, окружающей испаритель.
4.5. Второй закон термодинамики. Формулировки
второго закона термодинамики
Первый закон термодинамики ничем не ограничивает передачу различных видов энергии от одного тела к другому и их взаимопревращение. Он позволяет определить теплоту, работу, изменение внутренней энергии в различных термодинамических процессах, т.е. устанавливает лишь, что при переходе энергии из одного всегда в другой или при передаче её от одного тела к другому должен выполняться фундаментальный закон сохранения и превращения энергии. Однако он не устанавливает условий, при которых возможен тот или иной процесс, и проявление процесса.
Эти условия определяет второй закон термодинамики.
Второй закон термодинамики, как и первый, сформулирован на основе обобщения результатов практического опыта и наблюдений. Он устанавливает определённые ограничения на процессы передачи и превращения энергии.
Во-первых, это стремление всех естественных (самопроизвольных) процессов протекать в определённом направлении:
а) теплота самопроизвольно передаётся только от горячего тела к холодному;
б) вода течёт сверху вниз;
в) воздух перемещается из области высоких давлений в область низких давлений.
Во-вторых, все самопроизвольные процессы продолжаются до тех пор, пока не наступит равновесие между телами, участвующими в процессе:
а) переход теплоты от горячего тела к холодному телу продолжается до тех пор, пока их температуры не выравниваются;
б) сжатый воздух самопроизвольно вытекает из баллона (при открытом вентиле) до тех пор пока давление в нем не сравняется с атмосферным.
В-третьих, для осуществления искусственного (не самопроизвольного) процесса необходимо затратить внешнюю энергию.
Чтобы повысить давление воздуха, его надо переместить из области низкого давления в область высокого давления. Это искусственный процесс, и для его осуществления к воздуху в компрессоре ГТД подводят внешнюю работу.
Вышеперечисленные явления определяют условия, необходимые, для реального преобразования теплоты в работу и наоборот. Они отражены в различных формулировках второго закона термодинамики. Приведём эти формулировки.
1.Невозможен самопроизвольный процесс, единственным результатом которого была бы передача энергии путём теплообмена от холодного тела к горячему.
В этом виде закон сформулирован немецким физиком Р. Клаузиусом.
Мы подчеркнём слово “единственным”, так как передача энергии от холодного тела к горячему возможна, но при этом должна быть совершена работа внешними силами. Такие процессы осуществляются в холодильных машинах.
Схема процесса, запрещённого вторым законом термодинамики в формулировке Р. Клаузиуса, представлена на рис. 4.7,в.
2. Любой естественный процесс – есть переход от менее вероятного состояния к более вероятному.
Эта формулировка определяет направление термодинамических процессов. Наиболее вероятным является равновесное состояние термодинамической системы.
Изучение процессов взаимопревращения теплоты в работу и работы в теплоту показывает, что превращение работы в теплоту реализуется сравнительно просто и без ограничений. Так, например, за счёт трения, работу производимую двигателем, можно полностью преобразовать в теплоту. Иначе обстоит дело с превращением теплоты в работу. Вся многолетняя практика создания тепловых машин (двигателей) свидетельствует о том, что в любом из них нельзя полностью преобразовать подведённое к рабочему телу тепло в механическую работу.
Для периодического возвращения рабочего тела в исходное состояние в числе термодинамических процессов, составляющих цикл любой машины, обязательно имеется процесс, в котором происходит отвод части подведённой теплоты во внешнюю среду. Без этого процесса невозможно вернуть рабочее тело в исходное состояние после подвода теплоты и адиабатного расширения, путём только адиабатного сжатия. Это объясняется тем, что адиабатные процессы, соответствующие состоянию рабочего тела в начале и в конце процесса, различны. А различные адиабаты, как известно, не пересекаются. Учитывая сказанное, можно сформулировать второй закон по-другому.
3. В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую энергию, всего количества теплоты, полученного от источника энергии – нагревателя.
В этом виде второй закон сформулировал английский физик, один из основоположников термодинамики Уильям Томсон в 1851 году.
Таким образом, в любом тепловом двигателе, невозможно получение полезной работы без переноса части количества теплоты от нагревателя в холодильник.
На рис. 4.7. показана принципиальная схема работы любого теплового двигателя. Из рисунка видно, что полезная работа Lц может быть совершена только за счёт части энергии, выделившейся при сжигании топлива.
Даже если пренебречь всеми тепловыми потерями, то
Lц = Q1 – Q2,
где Q1 – количество теплоты от нагревателя, Q2 – количество теплоты, отданное холодильнику.
Другими словами, для работы теплового двигателя нужны три тела:
- нагреватель – источник энергии (перегретый при высоком давлении пар или газ при высокой температуре, созданный за счёт сгорания топлива);
- рабочее тело (обычно это газ, который совершает работу при расширении);
- холодильник (атмосфера или специальное устройство для охлаждения и конденсации отработанного пара).
Схема процесса, запрещённого вторым законом термодинамики в формулировке Томсона представлена на рис. 4.7,б.
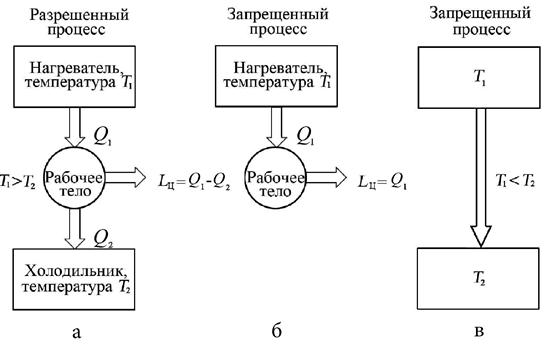
Рис. 4.7. Схемы термодинамических процессов, разрешённых и запрещённых вторым законом термодинамики: а – разрешённый процесс, б, в – запрещённые процессы
4. Невозможно построить непрерывно действующую машину, которая производила бы механическую работу за счёт охлаждения какого-либо источника теплоты до температуры более низкой, чем самое холодное из окружающих тел.
Эта формулировка интересна тем, что исключает возможность создания тепловой машины, которая могла бы использовать практически неограниченные запасы низкотемпературной тепловой энергии, содержащейся в мировом океане, в атмосфере.
Если бы удалось создать такую машину, то за счёт огромного количества тепловой энергии, которое соответствует охлаждению воды мирового океана на 1 К, можно было бы обеспечить потребность в энергии всего человечества на многие сотни лет.
Двигатель, в котором всё тепло какого-либо тела превращаются в работу, принято называть вечным двигателем второго рода. Другими словами, это двигатель, превращающий теплоту в работу без разности температур в окружающей среде.
И хотя его принцип действия не противоречит первому закону термодинамики, все попытки сконструировать такой двигатель, потерпели неудачу, так как не выполняется второй закон термодинамики. Поэтому В. Оствальд предложил наиболее краткую формулировку второго закона термодинамики.
5. Невозможно создать вечный двигатель второго рода.
Рассмотренным особенностям передачи и превращения тепловой формы энергии можно дать следующее физическое объяснение. Как известно из молекулярной физики, тепловая форма энергии является энергией беспорядочного движения микрочастиц вещества. Работа же совершается за счёт упорядоченного, направленного перемещения отдельных макрообъёмов рабочего тела (тема 2, с. 53). В природе наиболее вероятным состоянием является беспорядочное движение, т.е. тепловое движение частиц. Поэтому работа легко полностью переходит в теплоту. Обратный переход от беспорядочного движения к упорядоченному, т.е. переход теплоты в работу, является переходом от более вероятного состояния к менее вероятному и поэтому ограничен.
4.6. Второй закон термодинамики и энтропия
Как известно, что все самопроизвольные процессы являются необратимыми. Если изолированная (замкнутая) термодинамическая система находится в начальном неравновесном состоянии, то внутри неё будут протекать самопроизвольные процессы обмена энергией между отдельными телами до тех пор, пока система в целом не придет в равновесное состояние. При этом энтропия отдельных тел, входящих в систему, может увеличиваться или уменьшаться, в зависимости от того, подводится к ним тепло или отводится.
Но энтропия изолированной системы в целом при этом будет только возрастать. Покажем это на следующем примере.
Рассмотрим изолированную (замкнутую) систему, состоящую из двух тел с температурой первого T1 и второго T2 (рис. 4.8.), считаем T1 > T2.
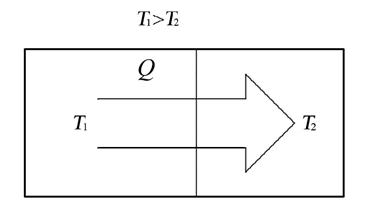
Рис. 4.8. Схема изолированной (замкнутой) системы
Тепло будет самопроизвольно переходить от горячего тела к холодному. Если от первого тела ко второму перешло некоторое количество теплоты Q при температуре T1, то энтропия первого уменьшится на величину:
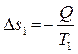 , (4.11)
, (4.11)
а второе тело, получившее количество теплоты Q при температуре T2 < T1, увеличивает свою энтропию на величину:
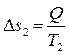 , (4.12)
, (4.12)
следовательно, в рассматриваемой изолированной (замкнутой) термодинамической системе энтропия изменилась на величину:
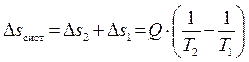 . (4.13)
. (4.13)
Так как T2 < T1, то Δsсист > 0. Очевидно чем больше разница температур T1 и T2, тем сильнее проявляется необратимость процесса, протекающего в системе, тем больше возрастает её энтропия. Нетрудно показать, что и для других необратимых процессов, при протекании их в изолированной системе всегда энтропия этой системы возрастает. Сказанное позволяет рассматривать энтропию как величину, характеризующую меру необратимости процессов, протекающих в замкнутых (изолированных) системах.
Если рассматривать обратимые процессы, энтропия системы сохраняется неизменной, то естьΔs = 0.
При достижении равновесного состояния в замкнутых системах её энтропия возрастает до максимального значения. Равновесная система не способна к производству работы, хотя она и располагает тем же запасом энергии, что и в начальном неравновесном состоянии. Равновесная термодинамическая система как источник работы мертва.
Поэтому можно дать очередную формулировку второго закона термодинамики – “энтропийную” формулировку. Энтропия всякой изолированной системы либо остается неизменной, либо увеличивается. В состоянии термодинамического равновесия в системе становятся невозможными самопроизвольные процессы.
Обращаем внимание на замкнутость (изолированность) системы как условие применяемости второго закона термодинамики. Аналитическая запись второго закона термодинамики в дифференциальной форме выражается уравнением (4.14)
ds ≥ 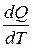 .(4.14)
.(4.14)
И наконец, какова же роль второго закона термодинамики в системе законов термодинамики. Ответить на этот вопрос довольно просто, если обратиться к следующему примеру.
Что происходит при опускании нагретого тела в холодную воду? Количество теплоты, отданное нагретым телом, равно количеству теплоты, полученному холодной водой, что соответствует закону сохранения энергии – первому закону термодинамики. Энтропия воды при этом возросла.
Теперь будем рассуждать так: пусть вода передаст свою энергию телу – вода остынет, тело нагреется. Это не противоречит первому закону термодинамики, но никогда не происходит в природе. Почему? Энтропия воды при таком процессе уменьшилась бы. А это запрещает второй закон термодинамики.
В настоящее время справедливость всех формулировок второго закона для макросистем подтверждена экспериментально и не подлежит сомнению.
4.7. Статистическая интерпретация второго закона термодинамики
Статистический метод позволяет объяснить, почему реальные процессы в природе необратимы, почему возрастает энтропия замкнутой системы, в чём состоит статистическая сущность второго закона.
Рассмотрим явления расширения идеального газа в пустоту. Пусть в начальный момент времени все молекулы находятся в левой половине сосуда, закрытой заслонкой (рис. 4.9,а). Если заслонку убрать, то газ займет весь объём сосуда (рис. 4.9,б).
При этом плотность, давление и температура газа во всех точках сосуда будут одинаковыми (наступит термодинамическое равновесие). Все указанные параметры не будут изменяться, хотя хаотическое движение молекул не прекращается.
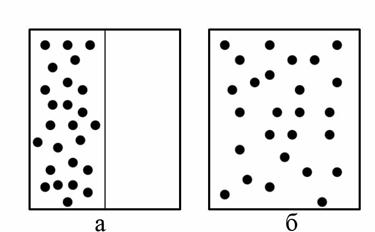
Рис. 4.9. Схема явления расширения идеального газа: а – молекулы находятся в левой половине сосуда, закрытой заслонкой, б – сосуд с открытой заслонкой
Сколько бы времени мы ни наблюдали в дальнейшем за газом, его молекулы самопроизвольно не соберутся в одной половине сосуда. Поэтому расширение газа в вакуум является необратимым процессом.
Обратите внимание на важное слово “самопроизвольно”. Мы, конечно, можем вернуть газ в левую половину сосуда, сжав его с помощью поршня, но самопроизвольно этот процесс маловероятен, особенно, если число молекул велико.
Теперь обратите внимание на слово “маловероятен”. Оказывается, все же существует возможность того, что все молекулы окажутся в одной половине сосуда. Для того чтобы характеризовать поведение частиц в системе, введём новое понятие – термодинамическую вероятность W. Она равна числу различных способов, которыми может, реализовано состояние макроскопической физической системы (макросостояние). Напомним, что в термодинамике состояние физической системы характеризуется определёнными значениями плотности, давления, температуры, объёма. Перечисленные величины определяют состояние системы в целом, её макросостояние. Однако при одних и тех же параметрах макросотояние системы частицы системы могут находиться в разных местах её объёма, иметь различные значения энергии и импульса. Каждое такое состояние называют микросостоянием.
Дадим более точное определение термодинамической вероятности. Термодинамическая вероятность W равна числу микросостояний, реализующих данное макросостояние. Ясно, что термодинамическая вероятность больше или равна единице: W ≥ 1.
При разработке молекулярно-кинетической теории учёные вынуждены были ввести вероятностные законы. Наиболее значительный вклад внесли Дж. Максвелл и Л. Больцман. В 1872 г. Больцман доказывает свою теорему, связывающую энтропию с вероятностью, и приходит к выводу, что “второе начало термодинамики оказывается вероятностным законом”.
Взгляды Больцмана были враждебно встречены всеми физиками. Полное признание его идеи нашли лишь в 1910 г., после создания броуновского движения А. Эйнштейном и её экспериментальной проверки Ж. Перреном (1870 – 1942).
В математическом виде второй закон термодинамики выражается формулой:
s = к·lnW,(4.15)
где s – энтропия;
к – постоянная Больцмана (к = 1.38∙10-23 Дж/К);
ln –натуральный логарифм (основанием является число е, равное примерно 2,7); W – термодинамическая вероятность.
Формула s = к∙lnW высечена на памятнике Больцману на Венском кладбище. Этим подчёркивается её важность для развития науки XX века. Формулу Больцмана по значимости можно поставить с двумя великими формулами, связанными с именами М. Планка и А. Эйнштейна.
Термодинамическая вероятность отличается от вероятности состояния термодинамической системы, которая всегда меньше или равна единице.
Микросостояния непрерывно изменяются, сменяя друг друга. Время пребывания в определенном макросостоянии пропорционально числу микросостояний W, которые реализуют данное состояние. Обозначив полное число микросостояний системы через Wо, можем записать выражение для расчёта вероятности макросостояния: 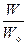 .
.
Вероятность макросостояния, характеризующая относительную частоту появления данного события, равна отношению числа микросостояний, реализующих макросостояние, к полному числу возможных микросостояний.
Чем больше термодинамическая вероятность W, тем больше вероятность данного макросостояния и тем большее время система будет находиться в данном состоянии.
Для равновесного состояния системы термодинамическая вероятность имеет максимальное значение. В таком состоянии система может находиться, очень долго.
Переход от маловероятных состояний к состояниям более вероятным определяет эволюцию системы и объясняет необратимость макроскопических процессов, несмотря на то, что законы, определяющие движение отдельных частиц, обратимы.
Рассмотрим пример, наглядно показывающий, как увеличение числа частиц в системе приводит к необратимости процессов, несмотря на обратимость законов движения частиц.
Пусть мы имеем в сосуде всего две молекулы. Предположим, что в начальный момент обе молекулы находятся в левой части сосуда. Возможно всего 4 способа распределения молекул между половинками сосуда (рис. 4.10.).
Из рисунка видно, что существует один способ размещения двух молекул в левой части сосуда (W = 1). В этом случае вероятность данного состояния равна: 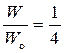 .
.
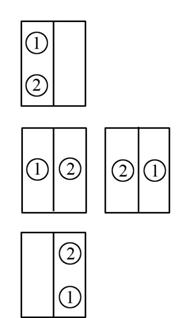
Рис. 4.10. Схема распределения 2-х молекул в половинках сосуда
Для трех молекул число возможных способов распределения молекул между половинками сосуда равно 8 (рис. 4.11.).
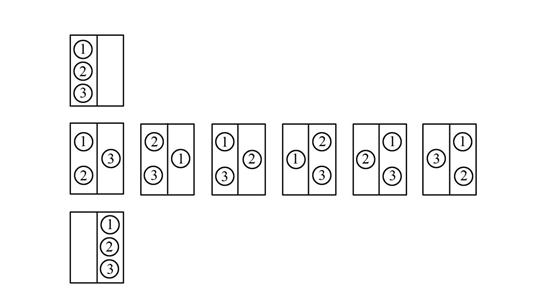
Рис. 4.11. Схема распределения 3-х молекул в половинках сосуда
Однако существует только один способ размещения трех молекул в левой части сосуда (W = 1), но так как Wо = 8, то вероятность данного события равна 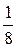 .
.
Для четырех молекул число возможных способов распределения молекул между половинками сосуда равно 16 (рис. 4.12.).
И опять существует только один способ размещения четырех молекул в левой части сосуда. В данном случае вероятность этого события равна 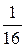 .
.
Так как 4 = 22, 8 = 23, 16 = 24, то можно сделать вывод, что для n молекул вероятность того, что все молекулы окажутся в левой части сосуда, равна: 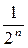 .
.
В реальном случае в газе число молекул очень велико (в одном моле любого газа содержится 6 · 1023 молекул), поэтому вероятность того, что все молекулы окажутся в одной половине сосуда, равна 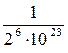 .
.
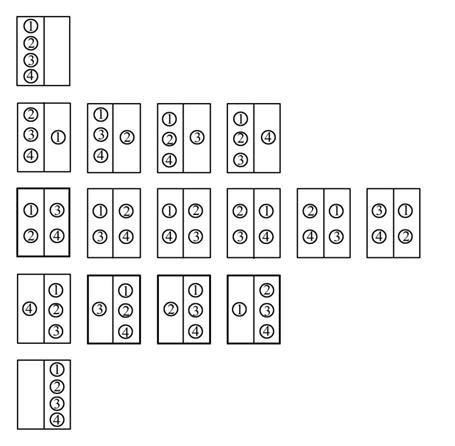
Рис. 4.12. Схема распределения 4-х молекул в половинках сосуда
Это значение настолько близко к нулю, что ситуация, когда все молекулы одного моля газа окажутся в левой части (или правой) части сосуда, никогда не реализуется.
На практике оказывается, что газ равномерно распределяется по всему сосуду, так как термодинамическая вероятность W равномерного распределения молекул максимальна.
Первый закон термодинамики не запрещает такого явления, когда в чайнике, стоящем на столе, нагревается за счёт охлаждения воздуха в комнате. Но этот процесс настолько маловероятен, что никогда не наблюдается.
Понятие “термодинамическая вероятность” помогает нам уяснить смысл второго закона термодинамики. Дело в том, что второй закон термодинамики имеет вероятностный характер. В отличие от закона сохранения энергии, который может быть применен к отдельным молекулам, атомам, электронам, ионам и другим частицам, второй закон термодинамики применим лишь к системам, состоящим из очень большого числа частиц.
Проанализируем формулу s = к∙lnW, которая в математическом виде выражает суть второго закона термодинамики. Из этой формулы видно, что энтропия s определяется только термодинамической вероятностью W. Возрастание энтропии при необратимых процессах есть следствие перехода от менее вероятных состояний к более вероятным. Ясно, что наиболее вероятное состояние – это состояние термодинамического равновесия.
Состояние макросистемы, которое реализуется малым числом микросостояний (W мало), называется упорядоченным.
Состояние, осуществляемое большим числом микросостояний (W очень велико), называется беспорядком, хаосом. Следовательно, равновесное состояние соответствует хаосу в макросистеме, т.е. наиболее неупорядоченному состоянию – состоянию с максимальной энтропией s.
Итак, энтропия является мерой неупорядоченности системы, а необратимость процессов можно трактовать как самопроизвольный переход системы от более упорядоченного состояния к менее упорядоченному, образно говоря, “от порядка к хаосу”.
Приведем примеры, иллюстрирующие полученный вывод:
- механическое движение упорядочено, а, следовательно, ему соответствует наибольшее число микросостояний по сравнению с беспорядочным тепловым движением. Поэтому механическая энергия самопроизвольно превращается во внутреннюю;
- любой вид энергии при её всевозможных превращениях, в конечном счете, переходит в энергию теплового движения, связанного с беспорядочным хаотическим движением частиц, так как любой другой вид энергии является мерой более упорядоченных движений. Например, энергия электрического тока связана с более упорядоченным движением заряжённых частиц по сравнению с тепловым, хаотическим движением;
- теплообмен самопроизвольно происходит от горячего тела к холодному до установления состояния теплового равновесия, так как этому состоянию соответствует максимальное число микросостояний.
Именно эту сторону понятия энтропии подчеркнул немецкий физик и математик А. Зоммерфельд, назвав энтропию царицей мира, которая предписывает всем процессам направление их протекания, а энергия выполняет лишь роль бухгалтера (пусть даже главного и великого), приводящего в равновесие дебет и кредит.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 4.1.
Доказать, что цикл Карно (идеальный тепловой двигатель) имеет наибольший термический КПД по сравнению с любым другим циклом в данном интервале температур.
Решение
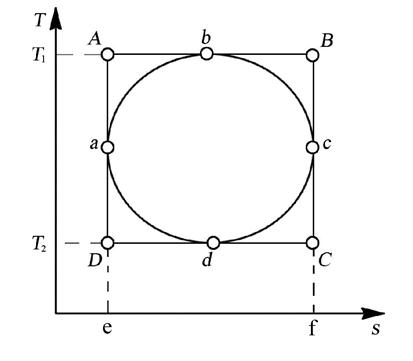 Для доказательства сравним в “T-s ”диаграмме (рис. 4.13.) цикл Карно (ABCD) с произвольным циклом (abcd), проходящим между теми же температурными границами.
Для доказательства сравним в “T-s ”диаграмме (рис. 4.13.) цикл Карно (ABCD) с произвольным циклом (abcd), проходящим между теми же температурными границами.
Рис. 4.13. “T-s ” диаграмма цикла Карно
Для цикла Карно имеем:
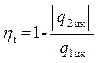 .
.
Из рис. 4.13. видно, что q2 цк = пл.eDcf, a q1 цк = пл.eABf. Соответственно для произвольного цикла имеем:
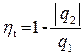 ,
,
где q2 = пл.eadcf, а q1 = пл.eabcf.
Сравнивая соответствующие площади, замечаем, что: q2 цк < q2, a q1 цк > q1, отсюда получаем неравенство:
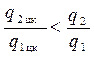 .
.
Следовательно,
ηt цк > ηt.
Таким образом, эффективность превращения теплоты в работу (термический КПД) в любом цикле не может быть больше, чем в цикле Карно, осуществляемом в том же интервале температур.
Задача 4.2.
Почему КПД идеального теплового двигателя меньше единицы?
Решение
На этот вопрос дает ответ математическая запись теоремы Карно:
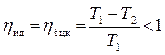 .
.
Могло ли быть иначе? Да, если бы существовал только первый закон термодинамики. Тогда можно было бы считать, что q2 цк = 0, и
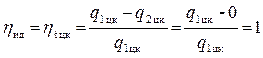 .
.
Сделать q2 цк = 0 нельзя, так как согласно второму закону термодинамики, энтропия рабочего тела в цикле должна остаться неизменной. Именно поэтому рабочее тело должно отдать “холодильнику” такое количество теплоты q2 цк, чтобы уменьшение его энтропии было бы равно её увеличению при изотермическом расширении.
Задача 4.3.
Газ совершающий цикл Карно, за счёт полученного от нагревателя количества теплоты, равного 2,5 кДж, производит работу 500 Дж. Каков КПД этого цикла? Во сколько раз абсолютная температура нагревателя больше абсолютной температуры холодильника?
Решение
Определяем коэффициент полезного действия тепловой машины работающей по циклу Карно, воспользовавшись уравнением (4.4)
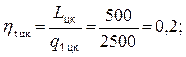
 ηtцк = 20 %.
ηtцк = 20 %.
Отношение абсолютной температуры нагревателя T1 и абсолютной температуры холодильника T2 определяется выражением (4.7)
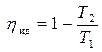 .
.
Отсюда имеем:
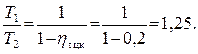
Задача 4.4.
Идеальная холодильная машина, работающая по обратному циклу Карно, отнимает от охлажденного тела количество теплоты, равное 2,8 кДж, и передаёт его более тёплому телу.
Температура охлаждаемого и тёплого тел соответственно равны (–10 °С) и 17 °С. Определите КПД цикла, количество теплоты, переданное тёплому телу за один цикл, и холодильный коэффициент машины.
Решение
Коэффициент полезного действия цикла:
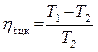 =
= 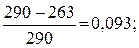 ηtцк= 9,3 %.
ηtцк= 9,3 %.
Так как:
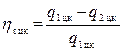 , то
, то
из равенства 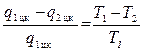
можно определить количество теплоты q1 цк переданное нагревателю за один цикл:
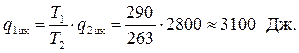
Теперь определяется холодильный коэффициент машины по уравнению (4.9)
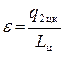 , где Lц= q1 цк– q2цк= 3100 – 2800 = 300 Дж.
, где Lц= q1 цк– q2цк= 3100 – 2800 = 300 Дж.
Таким образом, окончательно получаем, что
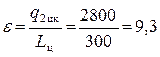 .
.
Задача 4.5. (решите самостоятельно)
Тепловую машину, работающую по циклу Карно с КПД равным 20 %, используют при тех же условиях как холодильную машину. Найдите её холодильный коэффициент.
Ответ: ε = 4
Задача 4.6. (решите самостоятельно)
Температура нагревателя идеальной тепловой машины, работающей по циклу Карно, равна 227 °С, температура холодильника 127 °С. Во сколько раз надо увеличить температуру нагревателя, чтобы КПД машины увеличился в 3 раза?
Ответ: В два раза
Задача 4.7. (решите самостоятельно)
Газ совершает цикл Карно, 75 % от количества теплоты, полученного от нагревателя, отдаёт холодильнику. Температура холодильника 273 К. Чему равна температура нагревателя?
Ответ: 364 К
Информация к размышлению
Использование внутренней энергии тепловыми двигателями таит в себе много вопросов. Сравним КПД (η) тепловых и электрических машин (табл. 4.1 и табл. 4.2).
Таблица 4.1
| Тепловой двигатель | η, % |
| Паровая машина стационарная Турбореактивный двигатель Газотурбинная установка (стационарная) Двигатель карбюраторный Дизель тракторный Дизель стационарный Тепловоз ТЭ3 Паровая турбина большой мощности при начальных параметрах пара: p = 3,5 МПа и t = 435 °С p = 9 МПа и t = 480 °С p = 17 МПа и t = 550 °С p = 24 МПа и t = 560 °С | ≈ 15 20…25 25…29 25…30 28…32 34…44 ≈ 28 36…37 |
Разница огромная: КПД электрических машин не опускается ниже 85 % и поднимается к теоретическому, разрешённому первым законом термодинамики (100 %); КПД тепловых двигателей не поднимается выше 40…45 %.
Все эти проблемы связаны с качественными особенностями внутренней энергии.
Таблица 4.2
| Электрическая машина | η, % |
| Электродвигатель Электровоз постоянного тока Электрический чайник с трубчатым герметическим нагревательным элементом Гидроэлектростанция большой мощности Гидрогенератор мощностью 120 кВт Линия электропередачи Волжская ГЭС им. В. И. Ленина – Москва Трансформатор большой мощности Гидрогенератор мощностью 500 МВт Турбогенератор мощностью 800 МВт Турбогенератор мощностью 1200 МВт | 82…98 ≈ 85 ≈ 86 ≈ 89 ≈ 90 ≈ 92,3 ≈ 98 98,2 98,8 98,9 |
Внутренняя энергия распределена между огромным числом частиц, образующих данную термодинамическую систему. В простейшем случае идеального газа – это кинетическая энергия хаотически движущихся частиц. Для более сложных термодинамических систем кинетической энергии поступательного движения добавляется кинетическая энергия, связанная с вращением и колебанием частиц, а также потенциальная энергия их взаимодействия. Это обстоятельство – распределение внутренней энергии между огромным числом хаотически движущихся и взаимодействующих частиц и приводит к тому, что полностью превратить её в механическую невозможно. Ведь при механической работе макроскопическое тело перемещается как целое. И вероятность того, что частицы вещества передадут всю свою энергию макроскопическому телу, стремится к нулю.
Проверьте, как Вы усвоили материал
1. Какой процесс называется термодинамическим циклом или круговым процессом?
2. В чём состоит практическое значение циклов?
3. Изобразите произвольный цикл в рабочей диаграмме, в котором происходит превращение теплоты в механическую работу.
4. Чем отличаются обратные циклы от прямых циклов?
5. Что оценивает термический коэффициент полезного действия цикла? Приведите математическую формулу этого коэффициента.
6. Из каких процессов состоит цикл Карно?
7. Сформулируйте теорему Карно.
8. В чём состоит практическое значение цикла Карно?
9. Как сформулировал второй закон термодинамики У. Томсон?
10. Как сформулировал второй закон термодинамики Р. Клаузиус?
11. Сформулируйте второй закон термодинамики, используя понятие энтропии.
12. Какова теоретическая модель теплового двигателя?
13. Почему нельзя создать идеальный тепловой двигатель с КПД, равным единице, если использовать в качестве холодильника тело при абсолютном нуле?
14. Как определяется КПД идеального теплового двигателя?
15. Противоречит ли создание вечного двигателя второго рода первому закону термодинамики?
16. Почему все реальные процессы необратимы?
17. Какие виды тепловых машин вам известны?
18. Назовите составные части любой циклической тепловой машины?
19. Как рассчитать холодильный коэффициент?
| <== предыдущая страница | | | следующая страница ==> |
| ТЕМА 3. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ | | | ТЕМА 5. ИДЕАЛЬНЫЕ ЦИКЛЫ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ |
Дата добавления: 2014-09-08; просмотров: 1914; Нарушение авторских прав

Мы поможем в написании ваших работ!