ТЕМА 5. ИДЕАЛЬНЫЕ ЦИКЛЫ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ

5.1. Особенности термодинамического метода исследования циклов тепловых двигателей

Основной задачей термодинамического исследования циклов тепловых двигателей является определение степени преобразования подведённого тепла в работу, т.е. определение термического КПД цикла и факторов, на него влияющих. В ходе исследования определяются также подведённое q₁ и отведённое q₂ тепло, работа цикла L_ц, оцениваются пути повышения эффективности цикла.

Теоретическое исследование реальных циклов тепловых двигателей является трудной задачей, поскольку превращение теплоты в работу у реального двигателя связано со многими сложными физическими, химическими и газодинамическими процессами, такими, как, например, горение топлива, теплоотдача от рабочего тела в стенки двигателя, течение газа в различных элементах двигателя и др. Изучение особенностей каждого из этих процессов является самостоятельной сложной научной задачей, которая рассматривается в теории двигателей.

В технической термодинамике изучаются идеальные циклы. В них реальные процессы идеализируются и отождествляются с обратимыми термодинамическими процессами, применительно к которым и проводятся все расчёты. Переход от реальных циклов к идеальным производится при следующих допущениях:

1. Идеализируется рабочее тело – химический состав его при осуществлении цикла принимается неизменным. Для циклов, в которых рабочим телом является газ, последний считается идеальным с неизменными физическими свойствами.

2. Процессы, составляющие цикл, считаются обратимыми. В связи с этим принимается, что трение и другие диссипативные эффекты отсутствуют.

3. Процесс горения заменяется условным обратимым процессом подвода тепла к рабочему телу.

4. Цикл считается замкнутым, процессы смены рабочего тела не рассматриваются, а процесс выбрасывания продуктов сгорания и их охлаждение в атмосфере, заменяются условным процессом отвода тепла от рабочего тела.

Составленный из таких процессов и при принятых допущениях цикл называется идеальным.

Термодинамическое исследование идеального цикла начинается обычно с построения его в “p-υ” или “T-s” координатах. Для этого необходимо задать параметры рабочего тела p₁, υ₁, T₁ в исходной точке 1 цикла и знать уравнения термодинамических процессов, составляющих цикл. Кроме того, для каждого конкретного цикла дополнительно задаются некоторые безразмерные параметры цикла, представляющие собой отношения одноименных параметров рабочего тела, относящихся к его состояниям в характерных точках цикла.

К числу таких параметров цикла относятся:

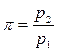– степень повышения давления, (5.1)

где p₁ – начальное давление рабочего тела,

p₂ – давление в конце процесса повышения давления рабочего тела;

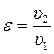– степень сжатия, (5.2)

где υ₁ – начальный удельный объём рабочего тела,

υ₂ – удельный объём в конце процесса сжатия рабочего тела;

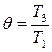– степень подогрева, (5.3)

где T₁ – начальная температура рабочего тела,

T₃ – конечная температура рабочего тела в процессах повышения давления (сжатия) и подвода теплоты;

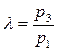– степень повышения давления при подводе тепла, (5.4)

где p₁ – начальное давление рабочего тела до подвода тепла,

p₃ – конечное давление рабочего тела после подвода тепла;

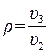– степень расширения при подводе тепла, (5.5)

где υ₂ – удельный объём в конце процесса сжатия рабочего тела,

υ₃ – удельный объём в конце процесса подвода тепла.

Эти безразмерные параметры определяют пределы изменения параметров рабочего тела в цикле при сжатии или при подводе тепла.

Общее значение термодинамического метода исследования циклов тепловых машин состоит в том, что это исследование позволяет установить наибольшее теоретически возможное значение термического КПД цикла, т.е. оценить предельную степень эффективности преобразования теплоты в работу в исследуемом цикле.

5.2. Схема устройства и принцип работы авиационного

газотурбинного двигателя (ГТД)

ГТД – тепловая машина, предназначенная для преобразования энергии сгорания топлива в кинетическую энергию реактивной струи и (или) в механическую работу на валу двигателя, основными элементами которой являются компрессор, камера сгорания, и газовая турбина (ГОСТ 23851-79 с. 2). Таким образом, характерной особенностью любого ГТД является наличие газогенератора, состоящего из компрессора, камеры сгорания и газовой турбины.

Рассмотрим схему и принцип работы ГТД.

На рис. 5.1. представлена схема турбореактивного двигателя (ТРД). Турбореактивный двигатель – ГТД, в котором энергия топлива преобразуется в кинетическую энергию струй газов, вытекающих из реактивного сопла (ГОСТ 23851-79 с. 3). Его основными элементами являются входное устройство (Н – В), компрессор (В – К), камера сгорания (К – Г), газовая турбина (Г – Т) и выходное устройство (Т – С).

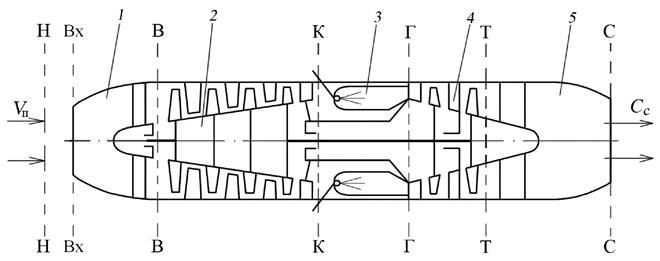Рис. 5.1. Схема турбореактивного двигателя (ТРД): 1 – входное устройство; 2 – компрессор; 3 – камера сгорания; 4 – газовая турбина; 5 – выходное устройство

Принцип работы ТРД состоит в следующем. Воздух в двигатель поступает через входное устройство, где скорость движения потока воздуха обычно уменьшается, а давление и температура возрастают. В компрессоре к воздуху подводится внешняя механическая энергия, вследствие чего его давление и температура увеличиваются. Скорость потока воздуха в компрессоре несколько уменьшается.

Из компрессора воздух поступает в камеру сгорания, где в нём сжигается топливо. В результате температура воздуха (теперь уже газа) повышается до 1200…1600 К. Скорость движения газа при этом растёт, а давление несколько уменьшается.

Далее газ проходит через турбину, где часть энергии сжатого и нагретого газа преобразуется в механическую работу, которая используется для вращения компрессора и привода вспомогательных агрегатов. Вследствие этого давление и температура газа в турбине уменьшаются. Другими словами, в турбине газ отдаёт ту механическую энергию, которая была подведена к воздуху в компрессоре. Таким образом, без учёта потерь энергия потока газа за турбиной отличается от энергии воздуха, поступающего в двигатель, на тепловую энергию, сообщённую ему в камере сгорания.

В выходном устройстве оставшаяся энергия газа используется для его разгона до скорости, значительно превышающей скорость полёта. Давление и температура газа при этом снижаются. В результате рассмотренных процессов воздух в двигателе получает ускорение. Это ускорение он приобретает в ходе воздействия на него элементов проточной части двигателя. В свою очередь, воздух (газ) действует на эти элементы в виде сил давления и трения. Равнодействующая этих сил – тяга двигателя – передается на самолёт.

5.3. Идеальный цикл ГТД (цикл Брайтона – Стечкина)

Цикл Брайтона – Стечкина – это цикл, осуществляемый с подводом тепла при постоянном давлении (p = const) и полном расширении. Этот цикл осуществляется в проточной части всех существующих типов авиационных ГТД и газотурбинных установок.

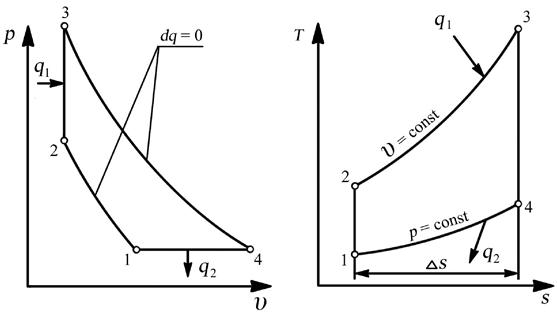
Идеальный цикл ГТД, изображенный на рис. 5.2. в “p-υ” и “T-s” координатах, состоит из четырех термодинамических процессов – двух обратимых адиабатных и двух изобарных процессов.

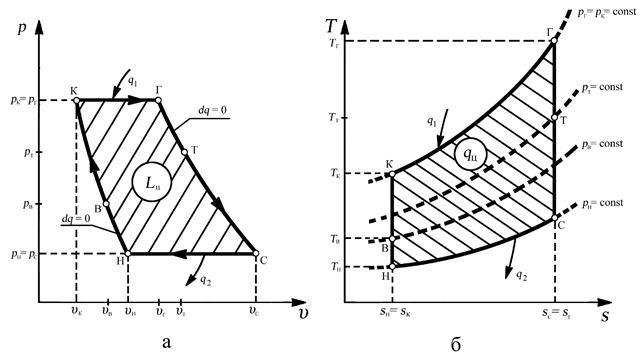
Рис. 5.2. Изображение идеального цикла ГТД с подводом тепла при p = const в диаграммах состояния: а – цикл в рабочей диаграмме; б – цикл в тепловой диаграмме

Линии на диаграммах изображают следующие термодинамические процессы:

1. Обратимый адиабатный процесс повышения давления воздуха, который осуществляется во входном устройстве (линия Н – В) и в компрессоре (линия В – К).

Из начальной точки “Н” при параметрах окружающей среды p_H и T_H происходит процесс обратимого адиабатного сжатия воздуха вплоть до выхода из компрессора в точке “К”. На начальном участке этого общего процесса между сечениями “Н” и “В” на рис. 5.2,а, сжатие воздуха в полёте происходит за счёт скоростного напора до входа в компрессор в точке “В”. С уменьшением скорости полета точка “В” перемещается к точке “Н” и при работе ГТД на земле на месте сливается с этой точкой.

2. Изобарный процесс подвода теплоты q₁ к воздуху, протекающего в камере сгорания (линия К – Г). От точки “К” до точки “Г” осуществляется изобарный процесс подвода теплоты q₁ в камере сгорания ГТД к рабочему телу. Температура рабочего тела (газа) в результате повышается и достигает максимального значения в цикле – Т_Г.

В процессе осуществления этих двух термодинамических процессов к рабочему телу извне сообщается энергия в виде теплоты, направленной на увеличение внутренней энергии. Таким образом, рабочее тело располагает большим запасом энергии, который отбирается в последующих термодинамических процессах расширения.

3. Обратимый адиабатный процесс расширения газа (понижения давления), осуществляемого в газовой турбине (линия Г – Т) и в выходном устройстве (линия Т – С).

От точки “Г” до точки “С” между сечениями на рис. 5.2. происходит общий процесс расширения газа по обратимой адиабате до давления окружающей среды p_C = p_H. На начальном участке этого процесса расширения газа происходит в турбине до точки “Т” между сечениями “Г” и “Т” на рис. 5.2., а затем расширение продолжается в сопле до точки “С”. Положение точки “Т” может быть различным для разных типов ГТД. У ТВД и вертолетных ГТД (ТВаД) точка “Т” практически совпадает с точкой “С”, т.к. расширение в сопле почти или совсем отсутствует. У одноконтурных ТРД точка “Т” занимает предельно верхнее положение, определяемое минимальной работой турбины, необходимой только для привода компрессора.

4. Условный изобарный процесс отвода теплоты q₂ от рабочего тела (газа) в холодильник (линия С – Н), роль которого выполняет окружающая двигатель атмосфера.

Этот процесс является процессом замыкающим цикл.

5.4. Работа и термический КПД цикла ГТД

Для оценки качества преобразования тепловой энергии, подведённой к воздуху в камере сгорания, в механическую работу и влияния на этот процесс различных факторов, определим работу цикла (L_ц) и термический КПД цикла (η_t).

Параметрами, определяющими L_ц и η_t являются:

а) Степень повышения давления воздуха в двигателе π_∑

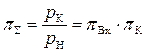, (5.6)

где π_Вх = 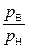– степень повышения давления воздуха во входном устройстве;

π_К = 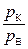– степень повышения давления воздуха в компрессоре;

p_К – давление воздуха за компрессором;

p_Н – давление воздуха на входе в двигатель.

б) Степень подогрева воздуха в двигателе

θ = Т_Г / Т_Н , (5.7)

где Т_Г – температура газов перед турбиной;

Т_Н – температура воздуха на входе в двигатель.

Если выбрать значения π_∑, θ и задать начальные параметры воздуха p_H, T_H, ρ_H (они легко определяются, если задать высоту и скорость полета), то можно определить L_ц и η_t, используя следующую методику:

1. Определяются параметры рабочего тела в характерных точках цикла.

Точка Н. Параметры p_H, T_H, ρ_H определяются по заданной высоте Н полета и скорости полета М_Н по стандартной атмосфере (ГОСТ 4401-81).

Точка К. Давление p_К определяется по формуле (5.6)

p_К = p_H ∙ π_∑ . (5.8)

Учитывая, что процесс повышения давления воздуха происходит по адиабате, и используя ранее полученные формулы адиабатного процесса (3.34), (3.39), получим выражения для определения температуры Т_К и удельного объёма υ_К:

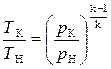
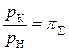
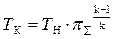(5.9)

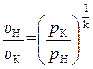
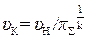. (5.10)

Точка Г. Так как процесс подвода теплоты изобарный, то давление в этой точке

p_Г = p_К = p_H · π_∑. (5.11)

Температура Т_Г определяется по заданной величине степени подогрева по выражению (5.7)

Т_Г = θ ∙ Т_Н. (5.12)

Теперь используя уравнение состояния идеального газа (1.11) определяется удельный объём υ_Г в точке “Г”

p_Г ∙ υ_Г = R_Г ∙ Т_Г 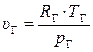. (5.13)

Точка С. Давление p_C = p_H, так как происходит полное расширение газа в цикле.

Процесс понижения давления (расширения) газа происходит по обратимой адиабате (линия Г – С) рис. 5.2. Используя формулу (3.39), получим выражения для определения температуры Т_С:

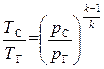, т.к. p_C = p_H и p_Г = p_К имеем

.

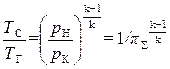Таким образом, величина температуры Т_С определяется по формуле:

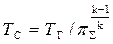(5.14)

Аналогично (5.13) определяем удельный объём υ_С в точке “С”.

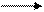p_С ∙ υ_C = R ∙ Т_C 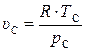(5.15)

Во всех промежуточных точках цикла, в том числе в точках “В” и “Т” можно определить значения интересующих параметров рабочего тела, что и будет сделано в дальнейшем по дисциплине “Теория авиационных двигателей”.

2. Определим количество тепла, подведённого к 1 кг рабочего тела q₁ и отведённого от него в холодильник q₂, используя найденные значения параметров состояния в характерных точках цикла.

Для изобарного процесса К – Г, используя формулы (5.9) и (5.12), получим

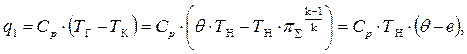(5.16)

где для упрощения дальнейших записей введём обозначение

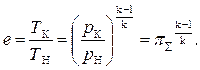(5.17)

Величина подведённого тепла q₁ изображается площадью фигуры s_HКГs_Cs_H, изображённой на тепловой диаграмме (рис. 5.2,б).

По линии С – Н протекает условный изобарный процесс с отводом тепла q₂. В результате простых преобразований с помощью формул (5.12), (5.15) получим:

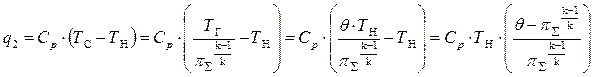(5.18)

Далее имея в виду (5.17) уравнение (5.18) приведем к виду:

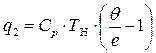(5.19)

А теперь полезно будет иметь зависимость между подведённым теплом в цикле q₁, отведённым в холодильник теплом q₂ и степенью повышения давления воздуха в двигателе π_∑. Уравнение (5.18) с помощью уравнения (5.16) приведём к виду:

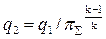. (5.20)

Величина отведённого тепла q₂изображается площадью фигуры s_HHCs_Cs_Hизображённой на тепловой диаграмме (рис. 5.2,б).

3. Определим термический КПД цикла, подставив (5.16) и (5.19) в (4.4):

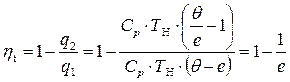(5.21)

или

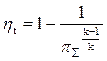. (5.22)

Таким образом,величина термического КПД идеального цикла зависит только от степени повышения давления воздуха в двигателе.Увеличение π_∑ является основным средством повышения η_t и соответственно уменьшения расхода топлива тепловых машин, работающих по циклу Брайтона – Стечкина. В современных двигателях π_∑ достигает значений 25…30 и более.

Из формулы (5.22) следует, что с увеличением π_∑ КПД цикла η_t непременно повышается и формально π_∑ → ∞,η_t → 1.

Зависимости η_t от π_∑ приведены на рис. 5.3. и рис. 5.4.

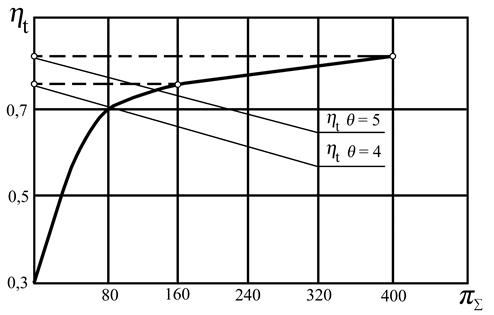
Рис. 5.3. Зависимость η_t = f (π_∑) для k = const

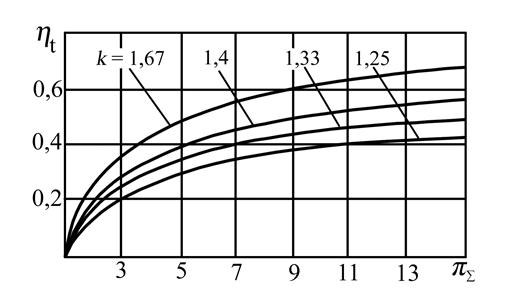
Рис. 5.4. Сравнительная зависимость η_t = f (π_∑) для разных значений коэффициента адиабаты

Увеличение термического КПД цикла объясняется тем, что с увеличением π_∑ возрастает степень понижения давления газа в выходном устройстве двигателя и соответственно снижается температура газа на выходе из двигателя. Поэтому уменьшается количество теплоты q₂, отводимого в атмосферу, и соответственно увеличивается количество теплоты q_ц = q₁ – q₂, преобразованной в полезную работу. Величина q_ц изображается площадью фигуры НКГСН на тепловой диаграмме (рис. 5.2,б).

Значение π_∑ возрастает при увеличении скорости и высоты полета, поэтому повышается экономичность двигателя. Так у современных ГТД при работе на земле КПД идеального цикла лежит в пределах 0,38…0,48, а в полёте увеличивается до 0,5…0,6.

4. И, наконец, определяется работа цикла L_ц, подставив в (4.3) значения q₁ и q₂ из (5.16) и (5.22) найдем выражение для работы цикла:

L_ц = q_ц = q₁ – q₂,

,

.

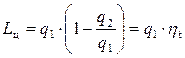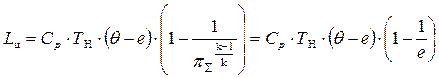И окончательно получаем работу цикла через параметры рабочего тела и параметры цикла:

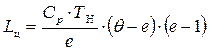. (5.23)

Как видно из (5.23), величина работы идеального цикла зависит от его начальной температуры Т_Н, степени повышения давления π_∑ и степени подогрева газа θ в цикле. С учетом уравнения (5.17) уравнение (5.23) преобразуем к удобному для дальнейшего исследования виду:

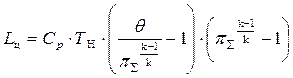. (5.24)

Из этих последних двух уравнений (5.23) и (5.24) следует, что работа цикла является функцией двух независимых параметров: степени подогрева θ (при заданной начальной температуре Т_Н) и степени повышения давления π_∑. С увеличением θ при любом значении π_∑ = const работа цикла возрастает. Это является одной из основных причин, в силу которой в мировом газотурбостроении (и не только в авиационном) господствующим направлением повышения энергетической эффективности ГТД является увеличение температуры газа перед турбиной. Но при этом возникают большие трудности, связанные с обеспечением надежности и ресурса высокотемпературных элементов ГТД. Так за последние примерно 50 лет с начала широкого применения ГТД (с конца 40-х – начала 50-х годов прошлого века) максимальная температура Т_Г повысилась с ~ 1 050…1 100 К (~780…830 °С) до ~ 1 600 К (~ 1 330 °С).

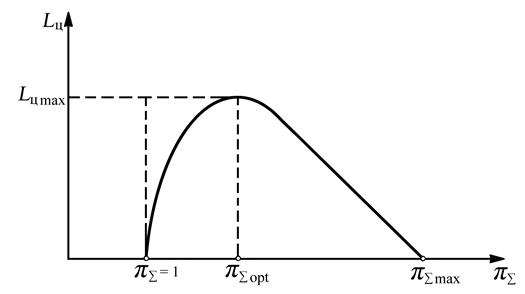
Рис. 5.5. Зависимость L_ц = f (π_∑) при θ = const

Влияние на работу цикла другого независимого параметра цикла π_∑ при θ = const, как видно из уравнений (5.23) и (5.24) неоднозначно. Формулы показывают, что L_ц обращается в нуль при двух значениях π_∑, соответствующих е = 1 и е = θ или с учётом уравнения (5.17) имеем:

что L_ц = 0 при 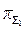= 1 и L_ц = 0 при 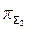= = 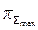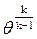. (5.25)

Очевидно, что между этими крайними значениями имеется некоторая оптимальная величина 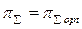, при которой работа цикла достигает своего максимального значения.

Для определения π_{∑ opt} продифференцируем уравнение (5.23) и производную приравняем нулю:

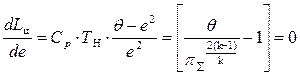, (5.26)

отсюда следует, что

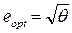или 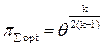, (5.27)

из (5.27) имеем

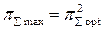. (5.28)

Как видно из (5.27) оптимальная степень повышения давления в идеальном цикле для данного рабочего тела зависит только от степени подогрева θ. С ростом θ растет и величина π_{∑ opt}. Зависимость работы цикла от степени повышения давления при различных значениях степени подогрева показана на рис. 5.6.

На рис 5.6. видно, что температура газа перед турбиной очень сильно влияет на работу цикла при любых π_∑. При оптимальных π_{∑ opt} максимальная работа цикла L_{ц max} с увеличением θ от 4-х до 5, т.е. на 25 %, возрастает на 50 %. При этом π_{∑ opt} повышается с 13 до 20.

Подставив из (5.27) 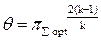в (5.24) получим выражение для максимальной работы цикла:

,

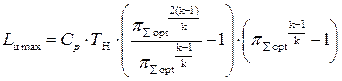Далее, выполнив ряд преобразований, получим

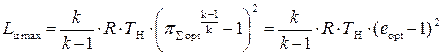. (5.29)

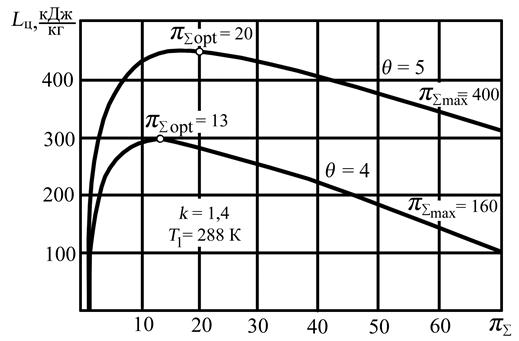
Рис. 5.6. Зависимость L_ц = f (π_∑) для разных значений степени подогрева θ

Как видно из рисунков (5.5. и 5.6.) при изменении π_∑ в интервале π_∑opt…π_∑maxработа и КПД цикла изменяются в противоположных направлениях. Поэтому рациональные значения следует выбирать в этом интервале, принимая то или иное компромиссное решение между работой цикла и его экономичностью. Более определенные рекомендации термодинамический анализ сделать не позволяет, необходимо дополнительно привлечь иные критерии технико-экономической эффективности.

Весьма наглядно влияние π_∑ на L_ц можно проиллюстрировать на циклах, изображённых на рис. 5.7., “p-υ” координатах при различных значениях π_∑ и при Т_Г = const(изотерма p= R·T_Г/υ). Площадь цикла максимальна L_ц= L_{ц max}при π_{∑ opt}. С увеличением и уменьшением π_∑ площадь цикла явно уменьшается и стремится к нулю в предельных случаях при π_∑ = 1 и π_∑ = π_{∑ max}, определяемых уравнениями (5.25). При этих значениях π_∑ цикла превращается соответственно в изобарный процесс p_H= p_Cmax= constи в обратимый адиабатный процесс Н – К_maxи К_max– Н.

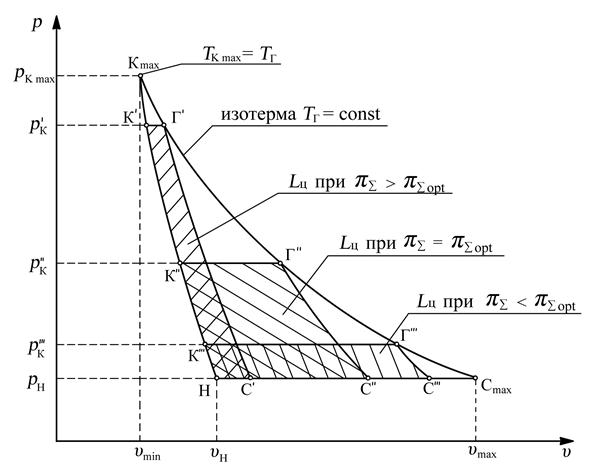
Рис. 5.7. Иллюстрация зависимости L_ц = f(π_∑) в

координатах “p-υ” для Т_Г = const

Хотя реальный ГТД строится на базе идеального, различия в энергетических показателях этих циклов весьма велики из-за наличия гидравлических потерь в процессах реального цикла. Поэтому необходимо иметь в виду, что после рассмотрения реального цикла в курсе “теория авиационных двигателей”, в результаты анализа обратимого цикла будут внесены существенные коррективы.

Рассмотренный цикл реализуется в ряде типов силовых установок. В авиации по этому циклу работают турбореактивные и турбовинтовые двигатели (ТРД и ТВД), вертолётные газотурбинные двигатели (ТВаД), а также прямоточные воздушно – реактивные двигатели (ПВРД). Цикл Брайтона – Стечкина реализуется и в газотурбинных установках (ГТУ), используемых как вспомогательные силовые установки на самолётах, в качестве корабельных, танковых и автомобильных двигателей, а также в стационарных энергетических устройствах. Отличительной особенностью ГТУ является то, что для получения работы, передаваемой к внешним потребителям (во внешнюю среду), у них используется газовая турбина.

Рабочим телом в этих силовых установках является в начале цикла воздух и далее – образующиеся в камере сгорания продукты сгорания топлива в воздухе (газ).

5.5. Цикл с подводом тепла при постоянном объёме (υ = const) и полном расширении (цикл Гемфри)

Цикл Гемфри, изображённый на рис. 5.8. в “p-υ” и “T-s” координатах, состоит из двух адиабатных процессов (сжатия 1–2 и расширения 3–4), изохоры 2–3 с подводом тепла q₁ и изобары с отводом тепла q₂.

Рис. 5.8. Цикл Гемфри в диаграммах состояния

Для исследования цикла зададим параметры рабочего тела p₁, Т₁ в исходной точке 1, степень повышения давления в процессе сжатия π и степень повышения давления в изохорном процессе подвода тепла .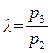

Подведённое тепло q₁определяется по формуле:

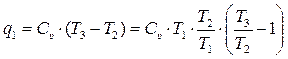. (5.30)

Здесь

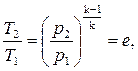
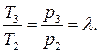
Подставляя эти отношения температур в (5.30), получим

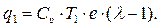(5.31)

Отведённое тепло q₂определяется по формуле

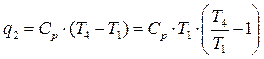. (5.32)

Из диаграммы цикла в “T-s” координатах для процессов 2 – 3 и 1 – 4 следует ∆s_{2 – 3}= ∆s_{1 – 4}= ∆s. Поэтому

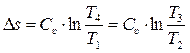. (5.33)

Отсюда

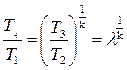. (5.34)

Подставив (5.34) в (5.32), получим

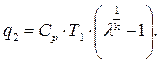(5.35)

Формулу для определения термического КПД цикла получим, подставив в (4.4) значения q₁и q₂:

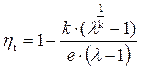. (5.36)

Термический КПД цикла Гемфри зависит от рода газа (k) и степеней повышения давления π и λ. При увеличении π и λ термический КПД цикла возрастает. Используя (5.31) и (5.35), получим формулу для L_ц:

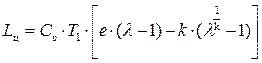. (5.37)

Для реализации цикла Гемфри в реактивных двигателях и газотурбинных установках следует обеспечить сгорание топлива (подвод тепла) при постоянном объёме. Это требует создания специальных клапанов, изолирующих камеру сгорания от остальной проточной части двигателя на время, необходимое для сгорания введённого в камеру количества топлива. Это мероприятие чрезвычайно усложняет конструкцию двигателя и делает её недостаточно надежной, в связи с чем до настоящего времени такие двигатели не созданы.

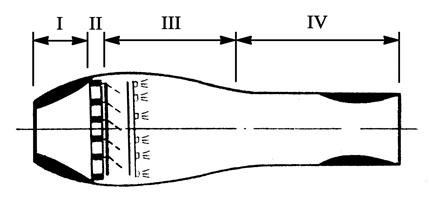К двигателям, в которых реализуется цикл, близкий к циклу Гемфри, относятся так называемые пульсирующие воздушно – реактивные двигатели. Схема такого двигателя представлена на рис. 5.9. Камера сгорания IIIразделяется с входным устройством Iспециальными клапанами II, которые открываются при заполнении камеры свежей порцией воздуха и топлива и закрываются при воспламенении топливо – воздушной смеси.

Рис. 5.9. Схема пульсирующего воздушно – реактивного двигателя

Выходное устройство IVсконструировано таким образом, что продукты сгорания предыдущей порции топлива не успевают покинуть его к моменту воспламенения новой порции. Таким образом, горение происходит в ограниченном (практически постоянном) объёме. Эти процессы повторяются с частотой, достигающей несколько сотен Герц. Данный тип двигателей не нашел широкого применения в технике вследствие низкой надёжности клапанного устройства.

5.6. Сравнение циклов Брайтона и Гемфри

Сравним эти циклы, полагая, что у них одинаковые значения степени повышения давления πи параметров рабочего тела в исходной точке 1 (p₁, Т₁) и в точке 4 (p₄, Т₄). Цель сравнения состоит в том, чтобы при заданных условиях выявить, какой цикл является более экономичным, т.е. имеет большее значение η_t.

Совместим сравниваемые циклы в “T-s” координатах (рис. 5.10.). Видно, что в данных условиях количество подведённого тепла в цикле Гемфри (q_{1 Г}) больше, чем в цикле Брайтона (q_{1 Б})

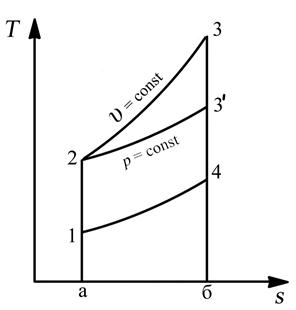пл. a23б> пл. a23'б

Рис. 5.10. Сравнение циклов Брайтона и Гемфри

Количество отведённого тепла в обоих циклах одинаково (пл. a14б). Поэтому на основании (4.4) можно утверждать, что при заданных условиях сравнения цикл Гемфри является более эффективным, т.е. имеет более высокое значение термического КПД. Однако по причинам, указанным выше, основное применение в технике получили реактивные двигатели и газотурбинные установки, в которых реализуется цикл Брайтона.

5.7. Цикл с регенерацией тепла

Регенерация тепла является одним из средств повышения термического КПД цикла. Регенерацией называется использование теплоты газов, отработавших в турбине, для подогрева сжатого воздуха, направляющегося из компрессора в камеру сгорания. На рис. 5.11. представлена схема газотурбинного двигателя, работающего по циклу Брайтона с регенерацией тепла. Основное отличие этого двигателя от ГТД, рассмотренного в (5.3), состоит в том, что он имеет теплообменный аппарат V, через который протекают холодный воздух, сжатый в компрессоре, и горячие газы, выходящие из турбины. Вследствие обмена теплом между ними происходит подогрев воздуха перед его поступлением в камеру сгорания и охлаждения горячих газов. Таким образом, при регенерации полезно используется тепло q_2p, что уменьшает количество тепла, отдаваемого в окружающую среду.

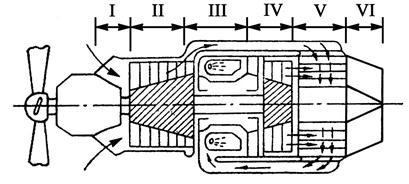
Рис. 5.11. Схема газотурбинного двигателя с регенерацией тепла

Очевидно, что регенерация возможна лишь в случаях, когда температура газа на выходе из турбины выше, чем температура воздуха после компрессора.

Изобразим в “T-s” координатах (рис. 5.12.) цикл Брайтона с регенерацией тепла. Он состоит из адиабатных процессов сжатия 1–2 и расширения 3–4, изобарного процесса подвода тепла в теплообменнике 2–2р и в камере сгорания 2р–3 и замыкающего цикл изобарного процесса отвода тепла в теплообменнике 4–4р и в окружающей атмосфере 4р–1. Подведённое к воздуху в теплообменнике тепло изображается на рис. 5.12. площадью a22pб и определяется по формуле

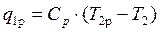. (5.38)

Отведённое в теплообменнике от горячих газов тепло q_2p изображается площадью c4p4д и равно:

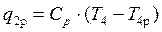. (5.39)

При отсутствии потерь тепла выполняется равенство

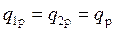. (5.40)

Максимальная температура, до которой может быть нагрет воздух в теплообменнике, равна температуре газов за турбиной (Т_{2p max} = Т₄). Поэтому

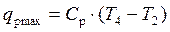. (5.41)

Степенью регенерации называется отношение действительного количества тепла, участвующего в регенерации, к максимально возможному:

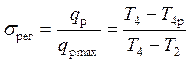. (5.42)

В реальных ГТД с регенерацией тепла 0 < σ_рег < 1. Определим термический КПД цикла Брайтона с регенерацией. С учётом передачи тепла через теплообменник

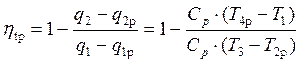. (5.43)

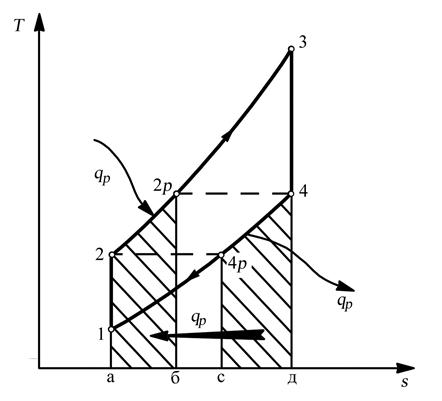
Рис. 5.12. Изображение цикла газотурбинного двигателя с регенерацией

тепла в тепловой диаграмме

В случае предельной регенерации (σ_рег = 1) Т_4р = Т₂, а Т_2р = Т₄. Тогда

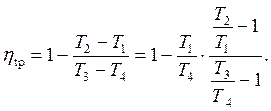(5.44)

В адиабатных процессах 1 – 2 и 3 – 4

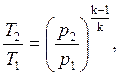
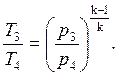
В цикле Брайтона p₁ = p₄ и p₂ = p₃, следовательно,

.

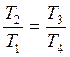После сокращения (5.44) приобретает вид:

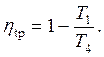(5.45)

Из (5.45) следует, что при постоянной исходной температуре рабочего тела Т₁ термический КПД цикла тем больше, чем выше температура после адиабатного расширения. Таким образом, применение регенерации тем эффективнее, чем выше температура газов перед турбиной.

Сравним при одинаковых параметрах цикла термические КПД циклов Брайтона с регенерацией тепла и без неё.

Преобразуем (5.43) к виду

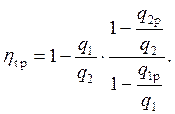(5.46)

Так как q₁ > q₂, а q_1p = q_2p, то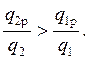

Следовательно, в (5.46) всегда

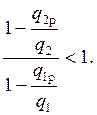
Без регенерации тепла, как известно,

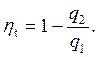(5.47)

Из сравнения (5.46) и (5.47) видно, что

η_{t p} > η_t ,

т.е. регенерация тепла повышает термический КПД цикла.

Регенерация тепла сравнительно широко применяется в газотурбинных установках. В авиации использование регенерации имеет место лишь в отдельных типах ГТД. Для широкого применения её в авиации необходимо создание лёгких и компактных теплообменников.

5.8. Цикл со ступенчатым подводом тепла

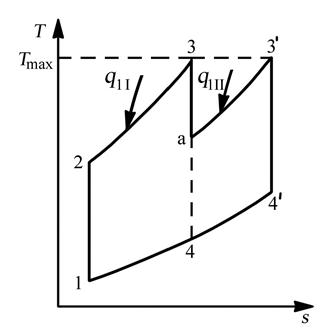Величина максимальной температуры Т₃ (Т_Г) в циклах ГТД и ГТУ обычно ограничивается условиями прочности турбины, что соответственно ограничивает работу цикла, а, следовательно, мощность (или тягу) двигателя. Повысить L_ц можно, используя ступенчатый подвод тепла. На рис. 5.13 в “Т-s” координатах показан цикл с двухступенчатым подводом тепла. В этом цикле тепло подводится в изобарных процессах 2–3 и а–3'. Следует обратить внимание на то, что подвод тепла в процессе а–3' происходит при меньшем давлении, чем в процессе 2–3. Видно, что по сравнению с циклом Брайтона 1–2–3–4 (рис. 5.15.) ступенчатый подвод тепла увеличивает L_ц (площадь цикла возрастает L_{ц ∑} = L_{ц I} + L_{ц II}). Однако КПД цикла при этом снижается. Для доказательства этого условно разделим цикл на два: I – цикл 1–2–3–4; II – цикл 4–а–3'–4'.

Рис. 5.13. Изображение цикла с двухступенчатым подводом тепла

в тепловой “Т-s” диаграмме

Запишем выражения для термодинамических КПД цикла I, цикла II и цикла со ступенчатым подводом тепла:

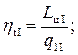
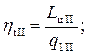
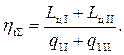(5.48)

Так как степень повышения давления в цикле II меньше, чем в цикле I,

η_{t II} < η_{t I}.

Решая совместно уравнения (5.48), нетрудно получить следующее соотношение:

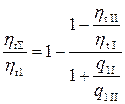. (5.49)

Из(5.49) видно, что поскольку η_tII < η_tI, то η_t∑ < η_tI. Следовательно, термический КПД цикла со ступенчатым подводом тепла меньше КПД исходного цикла Брайтона.

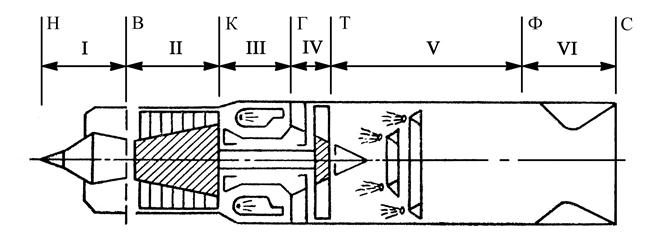
Рис. 5.14. Схема турбореактивного двигателя с

форсажной камерой сгорания (ТРДФ)

Цикл со ступенчатым подводом тепла применятся в авиации в турбореактивных двигателях с форсажной камерой сгорания (ТРДФ). Схема такого двигателя приведена на рис. 5.14. Термодинамические процессы протекают в этом двигателе следующим образом. Процесс 1–2 (рис. 5.15.) соответствует адиабатному сжатию во входном устройстве I и компрессоре II; процесс 2–3 – изобарному подводу тепла в основной камере сгорания III; процесс 3–а – адиабатному расширению в турбине IV; процесс а–3' – изобарному подводу тепла в форсажной камере сгорания V; процесс 3'–4' – адиабатному расширению в сопле VI; процесс 4'–1 – замыкающий изобарный процесс отвода тепла в окружающую среду. Отметим, что в ТРДФ температура газа в форсажной камере (Т₃') обычно выше температуры перед турбиной (Т₃) в виду отсутствия ограничений, связанных с работой турбины. Когда форсажная камера сгорания выключена, двигатель работает как ТРД по циклу Брайтона 1–2–3–4. Из выше сказанного следует, что η_{t ТРД} > η_{t ТРДФ}. ТРДФ обеспечивает по сравнению с ТРД увеличение тяги вследствие большей работы цикла, но имеет худшую экономичность из-за меньшего значения η_t .

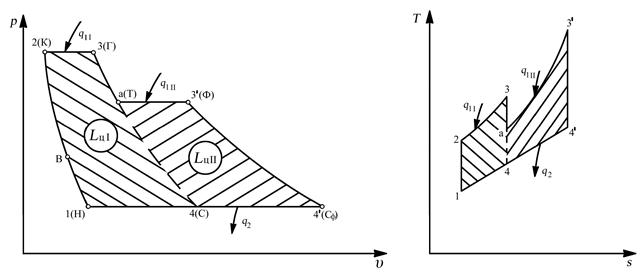
Рис. 5.15. Изображение цикла ТРДФ в диаграммах состояния

Таким образом, если к исходному циклу добавляются дополнительные ступени подвода тепла (при меньшем давлении), то это приводит к увеличению работы цикла, но ухудшению его экономичности. К такому же результату приводит и ступенчатый отвод тепла.

Если же в цикле со ступенчатым подводом и отводом тепла осуществляется и регенерация тепла, то это приводит как к росту L_ц, так и к увеличению η_t по сравнению с исходным циклом. В этом случае увеличением числа ступеней подвода и отвода тепла термический КПД идеального цикла может быть приближен к η_t обратимого цикла Карно.

5.9. Эксергетический метод термодинамического анализа

Как было указано выше, совершенство теплового двигателя может быть оценено величиной термического КПД (4.4), который показывает степень преобразования теплоты в полезную работу, а, следовательно, и долю потерь теплоты в цикле. В случае идеального обратимого цикла, каким является, например, цикл Карно, эти потери обусловлены только вторым законом термодинамики, т. е. неизбежной отдачей части подведённой теплоты в теплоприемник. Термический КПД идеального обратимого цикла Карно (4.7), таким образом, может служить определённым эталоном, в сравнении с которым оценивается совершенство реальных циклов тепловых двигателей с аналогичными значениями максимальной и минимальной температур в цикле.

В реальных циклах имеют место дополнительные потери, связанные с необратимостью реальных процессов. В этих случаях термический КПД (4.4) учитывает общие потери. Между тем для более полного и глубокого анализа совершенства тепловых двигателей, энергетических и холодильных установок, а также их отдельных элементов важно выделять потери, связанные с необратимостью реальных процессов. Это позволяет выяснить степень необратимости процессов в отдельных элементах и наметить пути их совершенствования. Одним из наиболее плодотворных методов такого анализа является эксергетический метод, общие представления о котором рассматриваются в данном вопросе.

В основе эксергетического метода лежит понятие эксергии – величины, означающей ту часть энергии, которая может быть превращена в полезную работу при обратимом переходе рабочего тела из рассматриваемого состояния в состояние равновесия с окружающей средой. Таким образом, эксергия характеризует работоспособность рабочего тела, т. е. определяет величину максимальной полезной работы, которая может быть получена в термодинамической системе “рабочее тело – окружающая среда”. Поскольку в большинстве тепловых двигателей, энергетических и холодильных установок имеет место непрерывный поток рабочего тела, важное значение имеет определение эксергии потока рабочего тела.

Рассмотрим неизолированную систему, состоящую из источника работы (рабочего тела) с параметрами Т₁, p₁ и окружающей среды с параметрами Т_о, p_о. Для производства максимальной работы рабочее тело из состояния 1 в состояние 0 должно быть переведено обратимо. Такой переход может быть проведен следующим образом. Вначале осуществляется обратимый адиабатный процесс 1–а(рис. 5.16.), в результате которого температура рабочего тела снижается от Т₁ до Т_о, а давление от p₁ до p_о, затем – обратимый изотермический процесс (Т_о = const), в котором за счёт теплообмена с окружающей средой давление рабочего тела достигает величины p_а. Заметим, что любая другая комбинация процессов между состояниями 1–0 является необратимой.

Таким образом, работа, совершаемая рабочим телом в процессах 1–а–0, является максимальной (L_max), она характеризует работоспособность источника работы (рабочего тела) в состоянии 1 по отношению к окружающей среде, находящейся в состоянии 0.

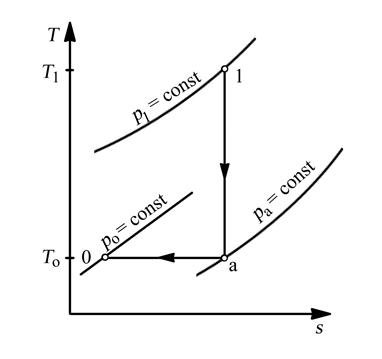
Рис. 5.16. К определению эксергии потока рабочего тела

Опуская вывод, приведём формулу L_max:

L_max = i₁ – i_о – T_о ∙ (s₁ – s_о), (5.50)

где i₁, s₁ – энтальпия и энтропия рабочего тела в исходном состоянии;

i_о, s_о – то же при достижении равновесия с окружающей средой.

Как указывалось, величину работоспособности рабочего тела называют эксергией (ex). Следовательно, эксергия потока рабочего тела в произвольном состоянии равна:

ex = (i – i_о) – T_о ∙ (s – s_о). (5.51)

Из (5.51) видно, что эксергия является функцией состояния. Однако в отличие от других функций состояния (внутренняя энергия, энтальпия, энтропия), её величина зависит как от состояния рабочего тела, так и от состояния окружающей среды. При термодинамическом равновесии окружающей среды и рабочего тела эксергия последнего равна нулю.

Эксергия рабочего тела изменяется при его переходе из одного состояния в другое. При этом на величину эксергии потока влияет обмен энергией с окружающей средой. Если, например, к рабочему телу подводится теплота q, то его эксергия возрастает на величину ex_q, которая представляет собой долю тепла и определяется из уравнения

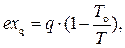(5.52)

где Т – температура источника теплоты.

Из (5.52) видно, что величина, стоящая в скобках, равна термическому КПД обратимого цикла Карно, осуществляемого между температурами источника Т и окружающей среды Т_о. Таким образом, эксергия подведённой теплоты q составляет только её “работоспособную” часть, т.е. ту часть, которая может быть преобразована в работу при заданном состоянии окружающей среды.

При подводе работы эксергия потока возрастает на величину ex_L, значение которой зависит от способа подвода работы.

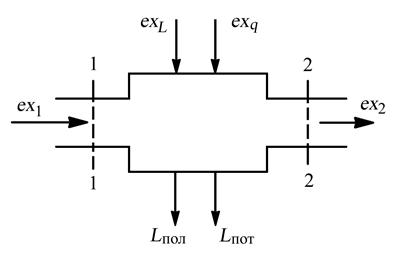Рассмотрим баланс эксергии (рис. 5.17.) применительно к какому–либо техническому устройству (тепловому двигателю, его отдельному элементу и т.д.).

Рис. 5.17. К составлению уравнения баланса эксергии

В этом случае эксергия потока рабочего тела на выходе из рассматриваемого устройства ex₂ равна алгебраической сумме эксергии рабочего тела на входе в него ex₁, эксергии подведённых теплоты и работы (ex_q, ex_L), а также затрат эксергии на совершение полезной работы L_пол и на потери вследствие необратимости процессов ∆L_пот:

ex₂ = ex₁ + ex_q + ex_L – L_пол – ∆L_пот. (5.53)

Заметим, что в (5.53) величины ex_q, ex_Lмогут быть положительными или отрицательными в зависимости от того, подводится теплота или работа к рабочему телу или отводится от него. Смысл полезной работы L_поли составляющие её величины определяются в зависимости от назначения рассматриваемого технического устройства и особенностей его работы. В частных случаях значения отдельных величин, входящих в (5.53), могут быть равны нулю. Из (5.53) при известных значениях ex₁, ex₂, ex_q, ex_Lи L_полможет быть определена величина потерь работы, связанная с необратимостью термодинамических процессов в рассматриваемом устройстве:

∆L_пот = (ex₁ – ex₂) + ex_q + ex_L – L_пол. (5.54)

В этом уравнении три первых слагаемых представляют собой расход эксергии на термодинамическую систему (ex_p), а последнее (L_пол) – затраты эксергии на полезный эффект (ex_п). Поэтому выражение (5.54) можно записать так:

∆L_пот = ex_p – ex_п . (5.55)

В случае обратимых процессов потери из-за необратимости отсутствуют (∆L_пот = 0), тогда из (5.55) следует:

ex_p = ex_п , (5.56)

т.е. все затраты эксергии в техническом устройстве являются полезными.

Для количественной оценки термодинамического совершенства какого–либо технического устройства используется эксергетический КПД, равный отношению полезно использованной эксергии ex_п к эксергии, израсходованной при осуществлении термодинамических процессов в рассматриваемом устройстве ex_p:

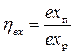. (5.57)

С учётом (5.55) можно записать

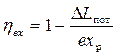. (5.58)

Из (5.58) видно, что величина эксергетического КПД зависит от степени необратимости термодинамических процессов и связанных с этим потерь ∆L_пот. При обратимых процессах ∆L_пот = 0 и η_ex = 1.

Заметим, что разделение эксергии на полезную (ex_п) и затраченную (ex_p) зависит от особенностей рассматриваемых технических устройств и в определённой степени произвольно. В связи с этим определения для эксергетических КПД различных устройств могут отличаться друг от друга. В каждом конкретном случае следует решать, какое из них более показательно.

5.10. Идеальные циклы двигателей внутреннего сгорания (ДВС)

Существует два основных обратимых цикла ДВС (как правило, поршневых, но не только). Это цикл с теплоподводом (сгоранием) при постоянном объёме, называемый циклом Отто, и цикл с теплоподводом (сгоранием) при постоянном давлении, называемый циклом Дизеля. Существует также цикл, в котором сгорание начинается при постоянном объёме и завершается при постоянном давлении. Этот цикл, называемый циклом Тринклера или Сабатэ, по своим показателям занимает промежуточное положение между циклами Отто и Дизеля.

5.10.1. Идеальный цикл ДВС с подводом тепла

при постоянном объёме (цикл Отто)

Начнем с цикла Отто, который приведён на рис. 5.18. в диаграммах состояния. Одновременно рассмотрим также рабочий процесс этого ДВС, для чего под циклом изображён цилиндр с поршнем, который может перемещаться внутри цилиндра в обе стороны от крайнего левого положения, называемого верхней мёртвой точкой (ВМТ), до крайне правого, называемого нижней мёртвой точкой (НМТ), и обратно. Возвратно – поступательное движение поршня (3) осуществляется кривошипно – шатунным механизмом (1). С помощью этого механизма работа цикла преобразуется в механическую энергию вращательного движения, используемую потребителем. У левого основания цилиндра (2) вблизи ВМТ расположены два клапана – впускной (5) и выхлопной (4), которые могут открываться и закрываться специальным механизмом, называемым механизмом газораспределения. Так же установлена электрическая свеча зажигания (6).

Рабочий процесс начинается при движении поршня от ВМТ к НМТ вправо при открытом впускном клапане. В цилиндр поступает топливовоздушная смесь (воздух с испарившимся бензином), которая предварительно образуется в карбюраторе. Вместо карбюратора применяется также непосредственный дозированный впрыск бензина в воздушный поток. В идеальном представлении процесс заполнения О – Н на рис. 5.18. происходит при постоянном давлении, но в действительности давление несколько пониженное. Процесс О – Н не входит в состав цикла, осуществляется не в закрытой, а в открытой термодинамической системе с переменной массой рабочего тела. Процесс заканчивается в точке “Н” при положении поршня в НМТ, и впускной клапан закрывается.

Цикл начинается в точке “Н” и происходит при постоянной массе рабочего тела. От точки “Н” осуществляется процесс сжатия по обратимой адиабате до точки “К” при движении поршня влево от НМТ к ВМТ. Оба клапана впускной и выпускной закрыты. В точке “К” от разряда в свече зажигания бензино– воздушная смесь воспламеняется и происходит её сгорание в течение очень короткого времени. Осуществляется подвод теплоты q₁ в идеальном представлении в изохорном процессе υ_К = υ_Г = const, давление и температура газа резко повышаются.

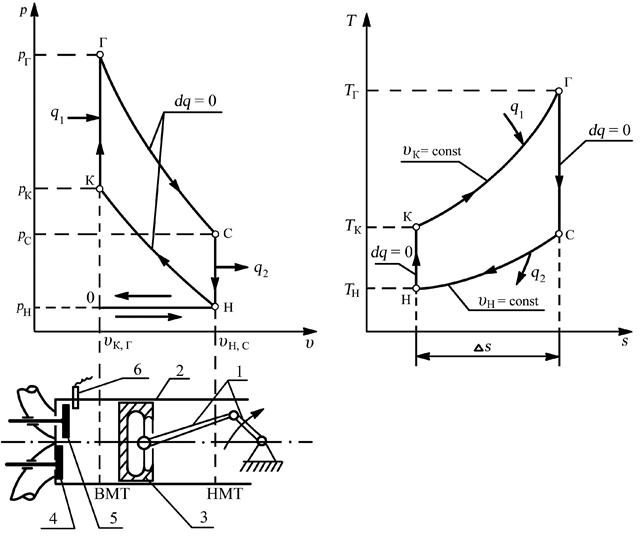
Рис. 5.18. Изображение идеального цикла ДВС с подводом тепла при постоянном объёме в диаграммах состояния: 1 – кривошипно-шатунный механизм; 2 – цилиндр; 3 – поршень; 4 – выхлопной клапан; 5 – впускной клапан; 6 – свеча зажигания

В реальном цикле зажигание смеси осуществляется ещё до подхода поршня к ВМТ, а процесс сгорания заканчивается после начала движения поршня вправо. Таким образом, реальный процесс теплоподвода не является строго изохорным.

От точки “Г” до точки “С” происходит расширение рабочего тела по обратимой адиабате при перемещении поршня вправо ВМТ к НМТ (рис. 5.18.). В точке “С” в идеальном представлении открывается выпускной клапан, и продукты сгорания выбрасываются в окружающую среду, где отводимая теплота q₂ рассеивается. Процесс теплоотвода происходит в изохорном процессе υ_С = υ_Н = const, температура и давление рабочего тела резко снижаются. Рабочее тело возвращается в исходное состояние в точке “Н”, и обратимый цикл завершается. В реальном цикле выпускной клапан открывается ещё до подхода поршня к НМТ, а выхлоп продолжается при движении поршня влево от НМТ, т.е. процесс теплоотвода далеко не является строго изохорным.

После завершения идеального цикла рабочий процесс ДВС ещё продолжается при движении поршня от НМТ к ВМТ при открытом выпускном клапане. Происходит выброс продуктов сгорания из цилиндра в атмосферу. В точке “О” на рис. 5.18. выпускной клапан закрывается, а впускной открывается. Только после этого завершается рабочий процесс ДВС, и вновь начинается процесс всасывания бензино–воздушной смеси. Процесс Н – О не входит в состав процессов идеального цикла и в реальных условиях происходит при несколько избыточном давлении.

Таким образом, идеальный цикл Отто состоит из двух обратимых адиабат Н – К и Г – С и двух изохор К – Г и С – Н и осуществляется за два хода поршня – от НМТ к ВМТ (сжатие) и от ВМТ к НМТ (расширение), т.е. за один оборот вала кривошипно–шатунного механизма. Рабочий процесс ДВС включает еще два процесса – всасывания О – Н и выталкивания Н – О, также осуществляемых за один оборот вала. Таким образом, весь рабочий процесс ДВС совершается за два оборота вала кривошипно–шатунного механизма, а поршень перемещается от ВМТ к НМТ и обратно 4 раза. Одно перемещение поршня называют тактом ДВС. Поэтому описанный рабочий процесс ДВС называютчетырехтактным. (Заметим, что существуют и двухтактные ДВС, у которых за один такт или ход поршня осуществляются сразу по два процесса: в одном – всасывание и сжатие, а в другом – расширение и выхлоп).

Из всех 4-х тактов рабочего процесса ДВС только в одном из них – в процессе расширения Г – С на рис. 5.18. происходит передача механической энергии потребителю. Поэтому этот процесс или такт называют рабочим ходом поршня от ВМТ к НМТ. В остальных 3-х тактах энергия на движение поршня только затрачивается в основном в такте сжатия рабочего тела в процессе Н – К. Эта энергия поступает от накопленного маховиком кривошипно–шатунного механизма за единственный такт – рабочий ход поршня, имея в виду, что энергия направляется и потребителю, ради чего собственно и осуществляется цикл ДВС.

Заметим, что ДВС, работающие по циклу Отто иногда называют карбюраторными (что не совсем справедливо) или двигателями легкого топлива, поскольку они используют бензин, более “легкий” по сравнению с дизельным топливом.

Перейдём к рассмотрению энергетических показателей обратимого цикла Отто. Количества подведённой и q₁ и отведённой q₂ теплоты в изохорных процессах К – Г и С – Н определяются уравнением (q_υ = c_υ·∆T), которое с учётом обозначений на рис. 5.18. запишется в виде

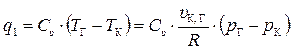, (5.59)

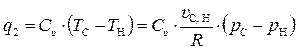. (5.60)

Отсюда получим уравнение для термического КПД, используя исходное уравнение (4.4)

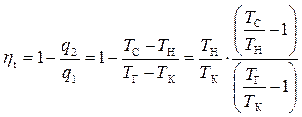. (5.61)

Из уравнения обратимой адиабаты 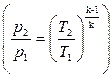, заменив отношение давлений обратным отношением удельных объёмов по уравнению 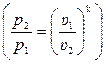, с учётом обозначений на рис. 5.18. получим для обратимых адиабат Н – К и Г – С следующие соотношения

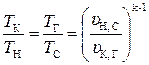или 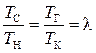. (5.62)

В теории ДВС сжатие рабочего тела принято оценивать отношением максимального и минимального удельных объёмов (или объёмов цилиндра), которое называется степенью сжатия:

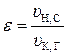. (5.63)

(В отличие от степени повышения давления p_К, как отношения давлений в конце и в начале сжатия в теории ГТД). С учётом соотношений (5.62), (5.63) уравнение (5.61) приобретает следующий вид:

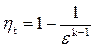. (5.64)

Как видно, термический КПД зависит только от одного параметра цикла – степени сжатия e. С ростом e термический КПД непрерывно повышается, и выгодно осуществлять, возможно, большие значения e. Однако, в двигателях Отто из-за сжатия не воздуха, а бензино–воздушной смеси и увеличения её температуры максимальные значения e ограничиваются возникновением детонации (взрывного горения), что недопустимо. В зависимости, главным образом, от качества бензина (его антидетонационных свойств) в двигателях Отто значения лежат в диапазоне e » 7…12. Как показывает практика, большие значения исключены. Например, при e = 10, h_t = 0,521, T_К = 691 K. Степень повышения давления .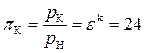

Характерной особенностью ДВС (в отличие от ГТД) является возможность осуществить предельно высокую температуру в процессе сгорания К – Г. Процесс сгорания весьма кратковременный (доли секунды), а затем следуют 3 хода поршня и процесс выхлопа С – Н. Конструктивные элементы в зоне горения успевают охладиться к началу следующего процесса горения. Кроме того, цилиндр снаружи охлаждается либо водой, либо воздухом, для чего предусматривается внешнее оребрение. Но это охлаждение гораздо менее существенно, чем периодичность сгорания. В результате с самого начала появления ДВС вопрос о повышении температуры не возникал, а для ГТУ с непрерывным процессом горения был и остаётся одним из основных.

Теплота, подводимая в изохорном процессе q_υ = q₁ в двигателе Отто, по существу является заданной. Она определяется как максимально возможная при сгорании топлива в количестве, необходимом для полного сгорания, т.е. при использовании всего кислорода, содержащегося в воздухе. На 1 кг бензино–воздушной смеси выделяемая теплота составляет q₁ » 2 600 кДж/кг. Уравнение (для изохорного процесса q_υ = С_υ·∆T) для q_υ = q₁ используется для определения максимальной температуры

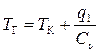. (5.65)

Эта температура получается очень высокой, пор

Дата добавления: 2014-09-08; просмотров: 3398; Нарушение авторских прав

Мы поможем в написании ваших работ!