ТЕМА 6. СВОЙСТВА ДВИЖУЩЕГОСЯ ГАЗА

6.1. Основные задачи газовой динамики

Газовая динамика – наука о движении газов с большими скоростями. Большими считаются скорости, близкие к скорости распространения звука в газе, равные этой скорости или же превышающие её.

При движении с такими скоростями в потоке газа наблюдается столь большие изменения давления и температуры, что заметным становятся изменения плотности при движении, проявляется такое свойство газа, как сжимаемость.

Если скорость движения газа значительно меньше звуковой, то изменения давления в потоке невелики и газ ведет себя как несжимаемая среда.

Газовая динамика является частью гидродинамики (гидроаэродинамики) – науки о движении жидкостей. Отличие этих наук заключается в том, что газовая динамика учитывает сжимаемость – явление, которое присуще газам, движущимся с большими скоростями.

При этом для описания поведения газа необходимо использовать уравнение состояния газа и уравнение изменения его энергии из-за деформации (сжатия и расширения) и из-за теплообмена. Это означает, что для описания явлений при движении газа с большими скоростями необходимо наряду с законами механики учитывать и законы термодинамики.

Процессы движения газа с большими скоростями все шире применяются в технике. Примерами таких процессов являются движение газов в соплах реактивных и ракетных двигателей, движение газа в каналах и лопаточных аппаратах газовых турбин и компрессоров, обтекание воздухом частей самолётов, ракет и снарядов, движущихся с околозвуковыми и сверхзвуковыми скоростями.

Для изучения таких процессов и принципов работы элементов ГТД необходимо знать основные законы движения воздуха и газа по газовоздушному тракту двигателя, процессы изменения параметров состояния в потоке газа, взаимодействие газового потока с ограничивающими его стенками. Эти законы устанавливает газовая динамика реактивных двигателей, которые отражены в основных уравнениях газовой динамики.

Основными задачами газовой динамики являются:

- изучение взаимных преобразований тепла, механической работы и различных видов энергии движущегося газа;

- определение сил, действующих со стороны движущегося газа на стенки каналов, в которых движется газ.

Таким образом, положения и уравнения газовой динамики являются основой теории реактивных двигателей и их элементов, а также методов их инженерного расчёта.

6.2. Структура основных понятий газовой динамики

Основные понятия газовой динамики, свойства газового потока, картина обтекания тел газовым потоком и системы основных уравнений, описывающих движение газа, представлены на рис. 6.1.

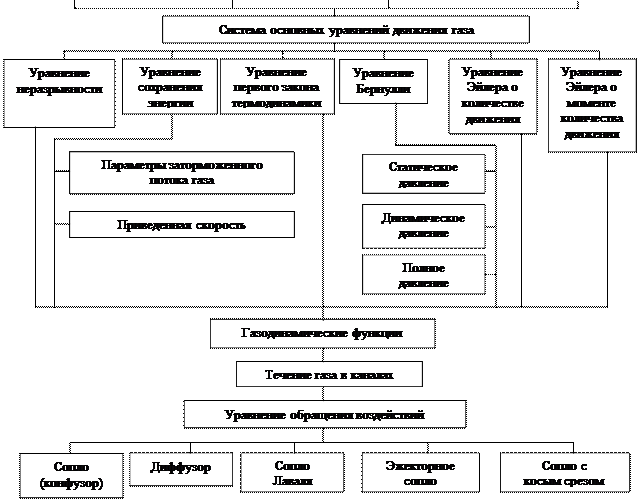
Рис. 6.1. Структура основных понятий газовой динамики авиационных двигателей

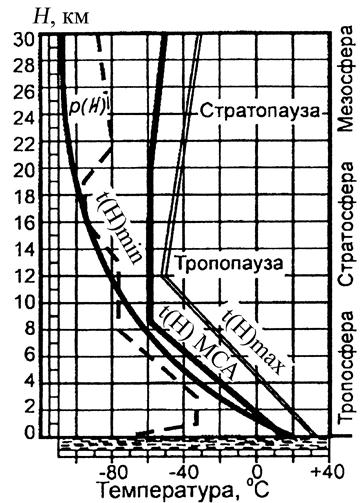
6.3. Международная стандартная атмосфера (МСА)

Необходимость сравнения результатов расчёта и лётных испытаний ЛА, ГТД проводимых в различных условиях, привела к созданию математической модели условной атмосферы. В соответствии с этой моделью, по высоте атмосфера делится на несколько слоёв, в пределах которых температура изменяется по определенным законам, довольно близко совпадающими с законами изменения по высоте среднегодовых значений температуры на средних широтах в летнее время (рис. 6.2.). Эти слои называются тропосфера (от греч. tropos – поворот, изменение), стратосфера (от лат. stratum – слой), мезосфера (от греч. mesos – средний, промежуточный), термосфера (от греч. terme – теплота, жар), экосфера (от греч. exo – вне, наружу). Сравнительно тонкие слои атмосферы, толщина которых измеряется десятками и сотнями метров, отделяющие друг от друга основные слои атмосферы, называются соответственно тропопаузой, стратопаузой, мезопаузой.

Рис. 6.2. Параметры МСА

Единая для всех государств международная стандартная атмосфера – условная атмосфера (модель), в которой распределение давления по высоте в поле силы тяжести получается из дифференциального уравнения гидростатики dp = – ρ·g·dH при определённых предположениях о распределении температуры по вертикали. В этом уравнении dp – дифференциал давления, Па; ρ – плотность воздуха, кг/м³; g – ускорение свободного падения, м/с²; dH – дифференциал высоты, м. Так как воздух сжимаем, его плотность зависит от давления и температуры в соответствии с уравнением состояния (Клапейрона – Менделеева)

,

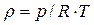где T – абсолютная температура, К; R – газовая постоянная, для воздуха R = 287,05 Дж/(кг·К).

В МСА за начало отсчёта высоты принят уровень Мирового океана при следующих нормальных условиях: ускорение свободного падения g_о = 9,807 м/с²; давление p_о = 101 325 Па (760 мм. рт. ст.); температура T_о = 288,15 К (t = 15 ^оС); плотность воздуха (вычисляется по температуре и давлению) ρ_о = 1,225 кг/м³; скорость звука (вычисляется по температуре) а_о = 340 м/с.

Для тропосферы (H = 0…11 000 м) принимают

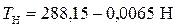; (6.1)

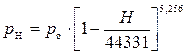; (6.2)

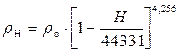; (6.3)

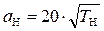. (6.4)

В стратосфере (до высоты H = 20 000 м)

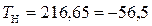°C; (6.5)

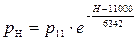; (6.6)

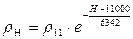; (6.7)

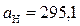м/с , (6.8)

где p₁₁ = 22,6 кПа = 170 мм. рт. ст.; ρ₁₁ = 0,364 кг/м³.

Рис. 6.3. Параметры МСА для малых высот

Подробные таблицы параметров стандартной атмосферы приводятся в литературе. В специальном математическом обеспечении ЭВМ есть стандартные программы, позволяющие рассчитывать параметры МСА.

Параметры МСА (изменение температуры и давления воздуха) для малых высот, на которых летают самолёты и вертолёты, приведены на рис. 6.3. здесь же приведены данные о распределении среднегодовых значений температуры t(H)_max и t(H)_min .

Все расчёты при проектировании ЛА и ГТД проводятся для условий МСА, что позволяет сравнить результаты расчётов и лётных испытаний нескольких ЛА и ГТД проводимых в различных климатических поясах. Результаты испытаний пересчитываются на параметры международной стандартной атмосферы, таким образом, все ЛА и ГТД “помещаются” в одинаковые условия – условия МСА.

6.4. Свойства движущегося газа

Движущийся газ обладает рядом свойств, из которых инертность, вязкость и сжимаемость оказывают наибольшее влияние на характер его движения.

Инертность характеризует способность газа сохранять состояние покоя или равномерного прямолинейного движения. Как известно из физики, мерой инертности тела является его масса. Инертность газа удобнее оценивать его плотностью, так как она является параметром состояния газа. Чем больше плотность газа, тем большее усилие необходимо приложить к газу, чтобы изменить величину и направление скорости его движения.

Вязкость характеризует способность газа сопротивляться сдвигу одних слоев относительно других. Существование вязкости газа объясняется хаотическим тепловым движением молекул, движущихся с различными скоростями, вследствие чего они перемещаются из слоя в слой и создают касательные силы взаимодействия между слоями. Эти силы называются силами внутреннего трения. Если силы внутреннего трения достаточно велики, то слои газа двигаются относительно друг друга без сдвига или скольжения. Характер движения потока газа называют слоистым или ламинарным. Если же силы внутреннего трения оказываются малыми по сравнению с силами движения, то слои газа сдвигаются относительно друг друга, вызывая завихрения. Характер движения газа при этом называют вихревым или турбулентным. Силы внутреннего трения преодолеваются за счёт энергии движущегося газа, которая преобразуется в теплоту. Эта теплота вновь подводится к газу, поэтому его полная энергия не изменяется (при условии, что теплота не идет на нагрев стенок канала). Однако качество энергии будет иное. Газ будет иметь меньшую механическую энергию и большую тепловую (внутреннюю), в результате снизится работоспособность газа.

Сжимаемость характеризует способность газа изменять свой объём (сжиматься и расширяться) при изменении давления или температуры. Количественно сжимаемость газа оценивается величиной Δρ/Δp, показывающей, как изменится плотность газа при изменении давления на единицу. Повышение температуры газа вызывает увеличение интенсивности хаотического движения молекул, и сжимать такой газ труднее, следовательно, сжимаемость его уменьшается. Понижение температуры увеличивает сжимаемость газа.

Упругость характеризует свойство газа возвращаться в исходное состояние после прекращения действия сил, вызвавших его деформацию. Естественно, что для воздуха такой деформацией может быть только деформация его объёма при всестороннем сжатии.

6.5. Скорость звука. Число Маха

Свойства сжимаемости и упругости воздуха проявляются в том, что всякое возмущение в нём, т.е. местное сжатие (местное повышение давления и плотности воздуха), распространяется в виде очень малых возмущений – колебаний давления и плотности. Эти колебания происходят со звуковыми частотами и распространяются в виде волн со скоростью звука. Таким образом, скорость звука a (скорость распространения звуковой волны в воздухе) характеризует упругость и сжимаемость воздуха.

Скорость движения волны можно определить из соотношения

a² = dp/dρ,

где p – давление воздуха в волне; ρ – плотность воздуха в распространяющейся волне.

Приближенно процесс распространения звуковой волны может рассматриваться как адиабатный, т.е. такой, при котором распространяющаяся волна газа не получает теплоты извне и не отдаёт её окружающей среде. В этом случае из уравнения обратимого адиабатного процесса (p·υ^k = const), которое запишем в виде p = const·ρ^k, и дифференцируя это уравнение и подставляя затем значение константы из исходного уравнения (p·υ^k = const), получим dp = const·k·ρ^k-1·dρ = 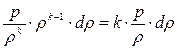, откуда 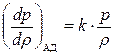и скорость звука выразится соотношением a = 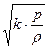и, используя уравнение состояния идеального газа p·υ = R·T, получим формулу (6.9) для определения скорости распространения звука:

a = 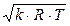, (6.9)

где k – показатель адиабаты;

R – газовая постоянная;

T – абсолютная статическая температура среды.

Из этой формулы следует, что величина скорости звука различна для различных газов и увеличивается в одном и том же газе с увеличением температуры. Положив по формуле (6.9) k = 1,4 и R = 287 Дж/(кг·К), получим приближенное значение для скорости звука в воздухе:

a ≈ 20 . (6.10)

Подсчитанная по этой формуле скорость звука в воздухе при 15 °С (288 К) равна 340 м/с, при 900 °С она достигает 600 м/с.

При изучении течения газа скорость его движения (c) в данном сечении сравнивают со скоростью звука (a) в том же сечении (местной скоростью звука).

Отношение скорости движения газового потока (c) к скорости звука (a) в данной точке потока называется числом М (число Маха, названо в честь австрийского учёного Э. Маха)

М = 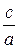. (6.11)

Число М потока является важным критерием, характеризующим сжимаемость газа (воздушного потока) под действием динамических сил.

В зависимости от числа М различают потоки:

- М < 1 – поток называют дозвуковым;

- М ≤ 0,4…0,5 – поток несжимаемый (т.е. поток газа можно рассматривать как поток жидкости);

- М = 0,8…0,9 – поток околозвуковой;

- М = 1 – поток звуковой, критический режим течения;

- М ≤ 1,3…1,6 – поток трансзвуковой;

- М > 1,8 – поток сверхзвуковой;

- М = 4…5 – поток гиперзвуковой.

6.6. Картина обтекания твёрдого тела потоком газа

6.6.1. Пограничный слой

Взаимодействие потока газа с внешней средой (твёрдым телом) осуществляется по контрольной поверхности (оболочке), где имеет место резкая разница в силах внутреннего трения. В результате силы молекулярного сцепления на границе двух сред приводят к тому, что скорость движения газа на контрольной поверхности равна нулю (рис. 6.4.). В соседних слоях, примыкающих к этой поверхности, силы внутреннего трения оказываются, значительно меньше и поэтому здесь возникает движение слоёв. Таким образом, градиент скорости при взаимодействии газового потока с твёрдым телом меняется от нуля на оболочке до скорости внешнего потока. Толщина слоя жидкости или газа, где происходит описанное изменение скорости, называется пограничным слоем.

Распределение сил внутреннего трения в пограничном слое приводит к тому, что непосредственно у твёрдого тела имеет место слоистый (ламинарный) характер течения, а по мере удаления от твёрдого тела этот характер либо сохраняется, либо изменяется (переходит в вихревой или турбулентный). Если же под влиянием внешних сил, турбулентный характер течения возникает, непосредственно на контрольной поверхности, то это явление называют отрывом пограничного слоя от твёрдого тела (рис. 6.4.).

Для преодоления сил внутреннего трения затрачивается энергия движущегося газа, которая, превращаясь в теплоту, вызывает нагрев газа и поверхности обтекаемого тела. Точка на поверхности тела, в которой поток газа утратил кинетическую энергию, соответствует точке отрыва пограничного слоя. В этой точке не действуют касательные напряжения, так как градиент скорости равен нулю. Правее точки отрыва, по направлению потока, частицы газа под действием положительного градиента давления начинают двигаться в обратную сторону, вследствие чего появляется срывная зона. Профили скоростей по нормали к течению правее точки отрыва имеют область отрицательных скоростей.

Отрыв потока сопровождается большими потерями давления. Кинетическая энергия образовавшихся вихрей не преобразуется в давление внизу, по течению, а необратимо переходит в теплоту. За точкой давление меньше, чем в местах безотрывного обтекания. Поэтому при обтекании с отрывом равнодействующая сил давления всегда имеет составляющую, направленную против потока. Эта составляющая называется сопротивлением давления.

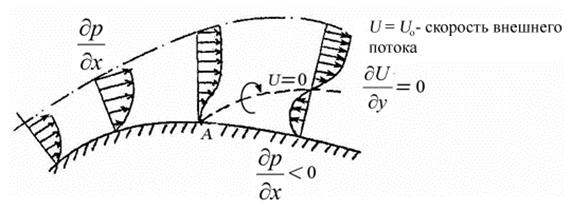
Рис. 6.4. Схема образования отрыва пограничного слоя:

А – точка отрыва пограничного слоя

Таким образом, сопротивление обтекаемого твёрдого тела состоит из сопротивления трения и сопротивления давления. У хорошо обтекаемых тел отрыв пограничного слоя отсутствует, поэтому сопротивление трения является основным.

6.6.2. Ядро потока

Деление потока газа на примыкающий к контрольной поверхности пограничный слой и внешний поток, называемый ядром, облегчает изучение течения в целом. Ядро потока рассчитывается с помощью системы основных уравнений движения газа, пограничный слой – методами теории вязкой жидкости.

Отмеченная система уравнений движения газа включает:

1. Уравнение неразрывности;

2. Уравнение сохранения энергии;

3. Уравнение первого закона термодинамики;

4. Обобщенное уравнение Бернулли;

5. Уравнение Эйлера о количестве движения;

6. Уравнение Эйлера о моменте количества движения.

Вывод названных уравнений, их физическую сущность и практическое применение к газовым потокам будут рассмотрены в следующей теме.

6.7. Распространение малых возмущений в потоке

Любое тело при обтекании его потоком вызывает в нём малые возмущения (звуковые колебания), которые представляют собой малые изменения плотности и давления среды. Вначале они возникают в слое, непосредственно примыкающему телу, а затем, передаваясь от слоя к слою, распространяются по всем направлениям от тела со скоростью звука.

Малые возмущения в воздушной среде возникают при следующих обстоятельствах:

а) тело, назовем его источником возмущений, может находиться в состоянии покоя (V = 0) и оно обтекается воздушным или газовым потоком (с ≠ 0);

б) источник возмущений перемещается (V ≠ 0) в неподвижной воздушной среде (c = 0).

Подобный характер обтекания наблюдается постоянно при эксплуатации авиационной техники. Например, обтекание ЛА воздушным потоком при его движении в воздушной среде, обтекание движущимися воздушными и газовыми потоками элементов ГТД при его работе. Поэтому представляется целесообразным рассмотрение характера распространения малых возмущений в потоке в зависимости от скорости потока и их влияния на характер обтекания тела (источника возмущения) потоком.

Рассмотрим картину распространения малых возмущений в потоках газа, движущихся с разными скоростями.

6.7.1. Неподвижный газ, с = 0. Рассмотрим распространение малых возмущений от точечного источника в неподвижной воздушной среде.

Известно, что малые возмущения от неподвижного источника распространяются в неподвижной воздушной среде в виде концентрических сфер, проекции которых на плоскость изображаются в виде концентрических окружностей радиусом

,

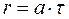где а – скорость звука, м/с;

τ – время, с.

Передний фронт звуковой волны (граница уплотнения) за первую секунду после возникновения звуковой волны пройдет по всем направлениям путь, численно равный скорости звука а (рис. 6.5,а), за вторую секунду – путь, равный 2а, за третью секунду – 3а и т.д. В невозмущенной воздушной среде малые возмущения (звуковые волны) распространяются симметрично по отношению к источнику (рис. 6.5,а).

6.7.2. Скорость газа меньше скорости звука, с < а. В движущемся потоке звуковые волны распространяются не только в радиальных направлениях, но еще и сносятся потоком. За первую секунду центр волны снесется потоком от источника на расстояние, численно равное скорости потока с (рис. 6.5,б). За это же время радиус сферы станет численно равным скорости звука а. К концу второй секунды расстояние между центром этой волны и источником станет равным 2с, а радиус волны – 2а и т.д. При этом распределение звуковых волн становится несимметричным по отношению к породившему их источнику. С наибольшей скоростью, равной сумме (с + а),эти волны распространяются в направлении потока и с наименьшей скоростью, равной (а – с),распространяются против течения.

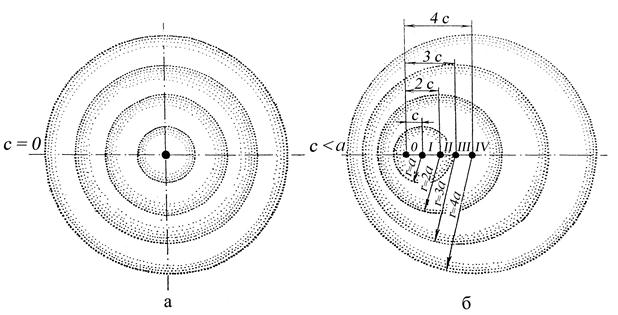
Рис. 6.5. Мгновенные изображения звуковой волны, распространяющейся в покоящемся (а) и в дозвуковом (б) потоке воздуха к концу каждой секунды

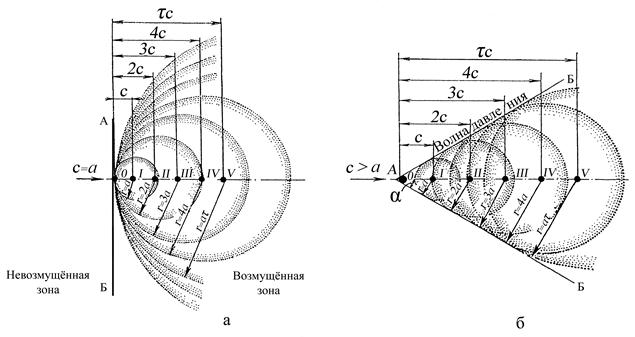Если скорость потока меньше скорости звука (с < а), волны распространяются не только по течению, но и навстречу набегающему потоку (рис. 6.6,б).

Рис. 6.6. Мгновенные изображения сферической звуковой волны в потоке воздуха, движущемся со звуковой (а) и сверхзвуковой (б) скоростями

В случае движения источника возмущений (например, летательный аппарат) со скоростью меньше скорости звука возмущения от него опережают его. В результате появления малых возмущений впереди ЛА происходит изменение параметров среды. Поэтому струйки потока воздуха заранее подготавливаются к плавному обтеканию тела (ЛА) задолго до приближения к нему в зависимости от формы этого тела.

6.7.3. Скорость газа равна скорости звука, с = а.В этом случае с течением времени возмущения распространяются в потоке, но они никогда не могут проникнуть в область, находящуюся перед источником возмущений, т.е. левее линии АОБ (рис. 6.6,а). Возмущения накладываются друг на друга и образуют плоскую волну, проходящую по линии АОВ. Эта плоская волна разделяет поток на две зоны: слева от плоскости волны, куда не могут проникнуть возмущения – зона невозмущенного потока, а справа, где распространяются возмущения – зона возмущенного потока.

6.7.4. Скорость потока газа больше скорости звука, с > а. В сверхзвуковом потоке волны не могут распространяться против течения, поэтому они заполняют не все пространство вокруг источника возмущений, а только определенную его часть, вытянутую в направлении течения (рис. 6.6,б).

Эта область представляет собой конус с вершиной в источнике возмущений, который называется конусом возмущений или конусом Маха. Звуковые волны, накладываясь одна на другую впереди тела, в результате суммирования создают волну давления, разделяющую весь поток на две области – возмущенную внутри конуса и невозмущенную снаружи его. Таким образом, волна давления является огибающей поверхностью передних фронтов звуковых волн. На этой поверхности, показанной линиями АБ, происходит концентрация возмущений.

Из рис. 6.6,б следует, что угол α (угол Маха) между направлением скорости течения и образующими конуса волны давления может быть найден по формуле

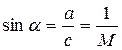. (6.12)

С увеличением числа М угол α уменьшается, а при уменьшении числа М – увеличивается. При М = 1 угол α = 90°, т. е волна давления развертывается в плоскость (рис. 6.6,а).

Источником звуковых волн в потоке может быть любое малое препятствие, например риска или бугорок на обтекаемой поверхности. Такое препятствие создает небольшое уплотнение, которое, стремясь сгладиться, распространяется в потоке. В сверхзвуковом потоке от каждого даже малого препятствия отходит волна давления, ограничивающая область распространения возмущений, вызываемых этим препятствием.

Рассмотрим обтекание входного устройства двигателя при дозвуковой скорости полёта. Если скорость движения самолёта меньше скорости распространения малых возмущений (скорости звука), то возмущения, созданные входным устройством распространяются навстречу потоку со скоростью а > V.

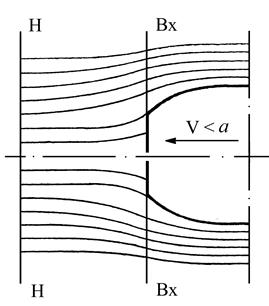Рис. 6.7. Обтекание воздухом входного устройства двигателя

при дозвуковой скорости полёта

В результате появления малых возмущений происходит изменение параметров среды ещё до встречи с входным устройством, т.к. поток “чувствует” находящееся впереди него препятствие задолго до приближения к нему, и поэтому струйки потока воздуха заранее перестраиваются к плавному обтеканию в зависимости от характера этого препятствия.

На рис. 6.7. показана схема обтекания потоком воздуха входного устройства воздушно – реактивного двигателя самолёта, летящего со скоростью V < а.

6.8. Обтекание сверхзвуковым потоком плоской стенки, выпуклых и вогнутых поверхностей

6.8.1. Обтекание плоской стенки

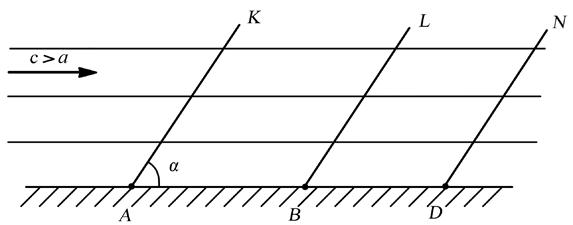Предположим, что сверхзвуковой поток движется параллельно какой-нибудь стенке со скоростью c > a (рис. 6.8.).

Рис. 6.8. Схема обтекания сверхзвуковым

потоком плоской стенки

Если в точках A, B, D на поверхности имеются какие либо препятствия, то вызываемые ими малые возмущения распространяются только правее граничных волн AK, BL, DN. Каждая из граничных волн наклонена к направлению скорости потока с под углом α, который определяется соотношением (6.12)

.

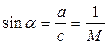Левее граничных волн AK, BL, DN малые возмущения, порожденные соответствующими источниками возмущений, т.е. точками A, B, D не могут распространяться навстречу сверхзвуковому потоку. Поэтому струйки потока в сверхзвуковом потоке заранее не могут подготовиться (как в случае c < a) к плавному обтеканию источника возмущений. Это является одним из характерных особенностей сверхзвукового потока.

6.8.2. Обтекание сверхзвуковым потоком выпуклых поверхностей

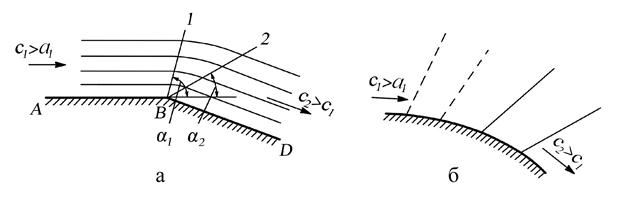Рассмотрим, как происходит обтекание сверхзвуковым потоком выпуклой поверхности, образующей внешний тупой угол ABD (рис. 6.9,а). Вдоль поверхности AB поток движется со скоростью c₁ > a₁. За точкой B струя (поток) расширяется, что приводит к увеличению скорости, поэтому при движении вдоль поверхности BD поток имеет скорость c₂ > c₁. Увеличение скорости сопровождается снижением температуры потока (Т₂ < Т₁) и скорости звука (a₂ < a₁).

Рис. 6.9. Схема обтекания сверхзвуковым потоком внешнего тупого угла (а)

и выпуклой криволинейной стенки (б)

Следовательно, c₂/a₂ > c₁/a₁ и М₂ > M₁.

Угловая точка В является источником слабых возмущений, поэтому от неё будут исходить волны давления B1 и B2, образующие соответственно углы α₁ и α₂ с направлением скоростей c₁ и c₂. Так как число М₂ > M₁, угол α₂ < α₁. Таким образом, волны возмущений расходятся от точки В.

Если сверхзвуковой поток обтекает плавную выпуклую поверхность (рис. 6.9,б), источником малых возмущений является каждая точка поверхности, поэтому от каждой точки будут исходить волны давления, не пересекающиеся одна с другой.

Таким образом, при обтекании сверхзвуковым потоком выпуклых поверхностей волны давления рассеиваются, а поток, расширяясь, ускоряется и движется вдоль поверхности со скоростью c₂ > c₁ (рис. 6.9,а,б).

6.8.3. Обтекание сверхзвуковым потоком вогнутых поверхностей

По иному происходит обтекание сверхзвуковым потоком вогнутых поверхностей. В этом случае вместо расширения происходит сужение струи, вызывающее уменьшение скорости потока. Углы наклона волн давления вдоль потока увеличиваются, что приводит к их пересечению и образованию сильного возмущения, которое называется скачком уплотнения или ударной волной (рис. 6.10,а).

При прохождении потоком скачка уплотнения, имеющего очень малую толщину (порядка 10^-3 мм), происходит мгновенное (скачкообразное) уменьшение его скорости и увеличение давления и температуры.

При обтекании сверхзвуковым потоком внутреннего тупого угла ABD (рис. 6.10,б) за точкой B происходит уменьшение скорости его движения (c₂ < c₁). При этом возрастают температура (Т₂ > Т₁) и скорость звука (a₂ > a₁). Поэтому c₂/a₂ < c₁/a₁и М₂ < M₁. Тогда угол α₂ граничной волны B2 должен быть больше угла α₁ волны B1. Так как до граничной волны B1 поток должен иметь

Рис. 6.10. Схема обтекания сверхзвуковым потоком вогнутой

криволинейной стенки (а) и внутреннего тупого угла (б)

скорость c₁, а после волны В2 – скорость c₂, как видно из рис. 6.9,б, в области между волнами В1 и В2 поток должен дважды изменить направление своего движения на противоположное, что невозможно. Поэтому поворот потока и изменение его скорости происходят на скачке уплотнения ВЕ, имеющего угол наклона α_ск, при чем α₁< α_ск< α₂.

Аналогично рассмотренному появляются скачки уплотнения впереди тел, обтекаемых сверхзвуковым потоком воздуха. Струи воздуха, вынужденно огибающие тело, искривляются так же, как при течении вдоль вогнутой поверхности. Наложение волн давления приводит к возникновению скачков уплотнения.

Скачки уплотнения образуются не только впереди тел, обтекаемые сверхзвуковым потоком воздуха, но и за ними. Эти скачки называют хвостовыми скачками уплотнения (хвостовыми ударными волнами), тогда как головные скачки уплотнения называют головными (ударными волнами) скачками уплотнения.

Скачки уплотнения отличаются один от другого формой и интенсивностью.

6.9. Скачки уплотнения и их особенности

Скачки уплотнения могут быть прямые и косые. Прямым скачком уплотнения называют такой скачок, поверхность которого перпендикулярна направлению набегающего потока (рис. 6.11,а). Если поверхность скачка наклонена по отношению к направлению набегающего потока, такой скачок уплотнения называют косым (рис. 6.11,б).

Прямые скачки уплотнения возникают перед телом, имеющим тупую закругленную переднюю кромку (рис. 6.12,а), или перед конусом (клином) с большим углом при вершине при движении со сверхзвуковой скоростью. Если сверхзвуковой поток обтекает конус (клин), имеющий малый угол при вершине, возникают косые скачки, начинающиеся от носка тела (рис. 6.12,б,в).

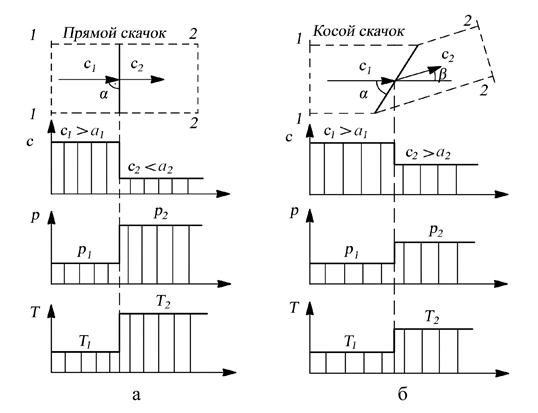
Рис. 6.11. Изменение параметров потока в прямом (а) и

косом (б) скачках уплотнения

Если скачок уплотнения начинается непосредственно на передней поверхности тела, то скачок называется присоединенным. Такие скачки возникают только на достаточно заостренных передних кромках (рис. 6.12,б,в). Если же передняя кромка предмета имеет тупой угол или закругление, то скачок уплотнения располагается на некотором расстоянии от тела; в этом случае скачок называется отсоединенным, или отошедшим (рис. 6.12, а).

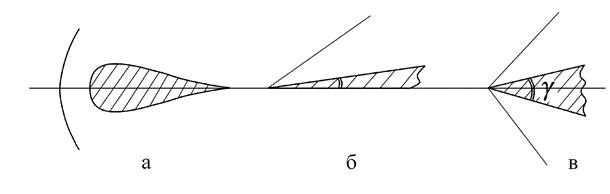
Рис. 6.12. Формы и схемы расположения скачков уплотнения

Интенсивность скачка уплотнения и его вид (прямой или косой) зависят от скорости набегающего потока формы обтекаемого тела. Чем интенсивнее скачок, тем в большей степени происходит снижение скорости за ним, а также увеличение давления и температуры потока. Наиболее интенсивным является прямой скачок, причём с ростом скорости его интенсивность возрастает. За ним скорость потока всегда становится дозвуковой и направление движения потока не изменяется. Скорость c₁ перед прямым скачком и скорость за прямым скачком c₂ связаны между собой следующей зависимостью:

c₁ · c₂ = 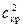, (6.13)

где c_кр – критическая скорость.

То есть чем больше скорость c₁до скачка, тем меньше скорость c₂ после скачка. Скорость за прямым скачком максимально может уменьшаться в шесть раз (c_1max /c_2min = 6). Косой скачок менее интенсивен, чем прямой. За ним поток изменяет направление движения и может быть дозвуковым или сверхзвуковым в зависимости от угла его наклона, который в свою очередь зависит от скорости потока и формы тела. Если угол наклона скачка не намного меньше 90°, он имеет большую интенсивность и поток за ним становится дозвуковым. При уменьшении угла наклона интенсивность скачка снижается, а при некотором его значении скорость за скачком, хотя и уменьшается, остается дозвуковой.

На рис. 6.13. представлена картина, объясняющая изменение направления движения потока за косым скачком.

Скорость потока перед скачком c₁ можно представить как геометрическую сумму двух скоростей:

c_1n = c₁·sinα – нормальная составляющая скорости потока до скачка;

c_1τ = c₁·cosα – тангенциальная составляющая скорости потока до скачка.

После косого скачка тангенциальная составляющая остается неизменной и она равна c_1τ = c_2τ. А для c_1n скачок будет прямым, поэтому нормально составляющая скорости c_2n будет всегда дозвуковой (c_2n < c_1n).

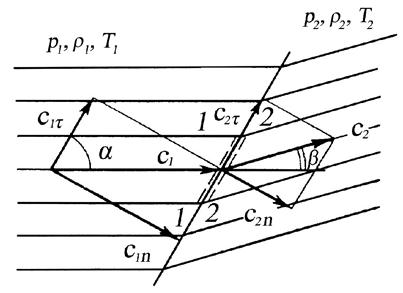Геометрическая сумма двух составляющих c_1n и c_2n дает результирующую скорость потока c₂ после косого скачка, которая поворачивается на некоторый угол β по сравнению с первоначальным направлением.

Рис. 6.13. Изменение направления

потока за косым скачком

Существуют предельные значения заострения тела, при которых возможно образование косых скачков уплотнения. Эти предельные значения зависят от скорости потока перед телом. Так, например, при М = 3 γ_пред = 34° (рис. 6.12,в). Это означает, что при сверхзвуковом обтекании клина с углом при вершине γ > γ_пред, возникает не косой скачок, а скачок уплотнения с криволинейным фронтом (головная ударная волна), поверхность которого не соприкасается с носиком тела.

При прохождении потоком скачка происходит качественное изменение его энергии: часть механической энергии преобразуется в тепловую (внутреннюю). Полная энергия потока до и после скачка не изменяется, однако за скачком поток имеет меньшую механическую энергию и большую тепловую (внутреннюю) энергию, поэтому его работоспособность снижается.

Вследствие преобразования энергии давления в теплоту при прохождении воздуха через скачок уплотнения, полное давление за скачком получается меньше, чем перед скачком.

Полным давлением называется давление адиабатно заторможенного потока. Оно является наибольшим возможным давлением при уменьшении скорости потока до нуля. Вследствие рассеяния энергии при прохождении воздуха через скачок уплотнения полное давление за скачком получается меньше, чем перед скачком. Потери полного давления в скачках уплотнений оцениваются коэффициентом восстановления полного давления σ_ск, который равен отношению полного давления 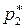за скачком к полному давлению 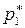перед скачком:

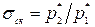. (6.14)

С ростом числа М полёта потери полного давления на скачке возрастают, следовательно, σ_ск уменьшается.

На рис. 6.14. показана схема организации торможения сверхзвукового потока в прямом скачке (рис. 6.14,а) и в системе косых скачков (рис. 6.14,б), при обтекании воздухом гондолы двигателя. Потери полного давления в косом скачке всегда меньше, чем в прямом, поэтому для снижения потерь энергии торможение потока необходимо осуществлять в системе косых скачков (рис. 6.14,б).

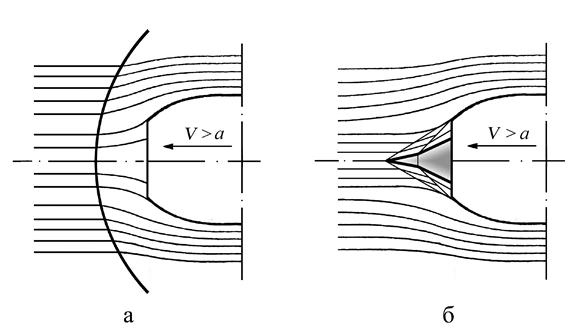
Рис. 6.14. Обтекание воздухом гондолы двигателя при полёте самолёта со сверхзвуковой скоростью: а – дозвуковое входное устройство, б – сверхзвуковое входное устройство

Из рассмотренных выше случаев обтекания сверхзвуковым потоком различных тел можно установить следующие характерные особенности сверхзвукового потока:

- ускорение сверхзвукового потока происходит в расширяющемся канале;

- слабые возмущения в сверхзвуковом потоке охватывают лишь часть пространства внутри конуса малых возмущений, малые возмущения не могут распространяться против сверхзвукового потока;

- если в дозвуковом потоке изменение скорости и параметров потока происходит ещё до встречи с препятствием, то в сверхзвуковом потоке, это точно известно, в скачке уплотнения;

- торможение сверхзвукового потока происходит не постепенно, а скачком. Невозможность предварительной перестройки, подготовки потока при подходе к препятствию является главной особенностью сверхзвукового потока.

Проверьте, как Вы усвоили материал

1. С какой целью принята международная стандартная атмосфера (МСА)?

2. Назовите основные свойства движущегося газа.

3. Что называется вязкостью и чем она обусловлена?

4. Дайте определение ламинарного и турбулентного потока.

5. Напишите формулу для определения скорости распространения звука.

6. Проанализируйте, какие факторы влияют на величину этой скорости.

7. Дайте определение числу Маха.

8. При каких значениях скорости потока газа можно рассматривать его как несжимаемую среду?

9. Почему в дозвуковом потоке параметры среды изменяются ещё до встречи с источником возмущений?

10. Что такое конус Маха и угол Маха?

11. В чём различие между слабыми и сильными возмущениями в потоке газа?

12. Почему торможение сверхзвукового потока происходит не постепенно, а скачком?

13. Укажите основные особенности прямых и косых скачков.

14. Какая из составляющих скорости потока, нормальная или тангенциальная, изменяется при переходе газа через фронт скачка уплотнения?

15. Летательный аппарат совершает полёт на высотах 5 и 10 км с одинаковой дозвуковой скоростью, отличается ли характер обтекания ЛА потоком на этих высотах?

16. Почему в сверхзвуковых входных устройствах торможение потока осуществляют в системе косых скачков?

Дата добавления: 2014-09-08; просмотров: 1424; Нарушение авторских прав

Мы поможем в написании ваших работ!