ТЕМА 7. ОСНОВНЫЕ УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ

7.1. Основные допущения, принимаемые в газовой динамике

Основная особенность авиационных ГТД состоит в том, что все процессы в них протекают в движущемся рабочем теле (газе). Теория и расчёт этих процессов базируется на термодинамическом анализе газового потока. Данный анализ, в свою очередь, основывается на первом законе термодинамики. Исходя из первого закона термодинамики, можно получить основные соотношения, описывающие энергетический баланс в потоке, и выявить характер изменения параметров рабочего тела. Для полной характеристики состояния движущегося газа (рабочего тела), кроме основных термодинамических параметров (р, Т, υ), необходимо знать и скорость движения газа (с)через данное поперечное сечение. Движение газов по каналам имеет свои закономерности, которые отражены в основных уравнениях газовой динамики.

Необходимо отметить, что в общем случае движение газа в элементах летательных аппаратов и силовых установок имеет сложный характер и уравнения, точно описывающие реальный поток, весьма громоздки, что затрудняет их использование для анализа и практических расчётов. Поэтому вывод уравнений газовой динамики осуществляется при следующих основных допущениях:

- течение газа считается стационарным (установившимся), т.е. все параметры газа (скорость, давление, температура, плотность) в любой точке потока неизменны во времени. В действительности всегда имеются пульсации потока, вызванные конечным числом лопаток, турбулентностью и другими причинами, но пренебрежение ими не приводит к заметным погрешностям в расчётах;

- считают, что в каждой точке данного сечения все параметры потока газа одинаковы. Такой поток называют равномерным. Изменение параметров происходит лишь в направлении движения. Уравнения, полученные при этом условии, строго верны лишь для элементарной струйки, поперечные размеры которой настолько малы, что в каждом ее сечении параметры потока практически постоянны. Следует отметить, что в реальных газовых потоках в пределах поперечного сечения параметры газа могут быть переменными. При использовании уравнений элементарной струйки для таких потоков рассматриваются средние для каждого сечения потока величины (средняя скорость, средняя плотность и т.д.).

Примером движения газового потока при таких допущениях можно считать во всех элементах ГТД во время его работы при неизменной частоте вращения, скорости и высоты полета.

7.2. Уравнение неразрывности (расхода)

Это уравнение позволяет рассчитать проточную часть двигателя и связывает параметры и скорость газа (рабочего тела) с площадью поперечного сечения газового потока и определить, таким образом, габариты ГТД.

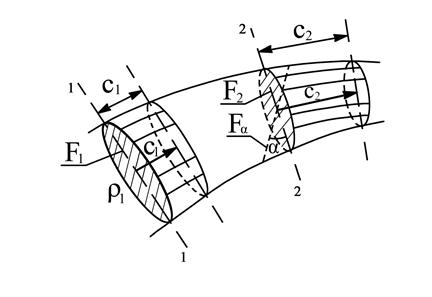Рассмотрим движение газового потока по каналу с непроницаемыми стенками переменного сечения (рис. 7.1.), в котором выделим произвольный участок между сечениями 1-1 и 2-2, перпендикулярными скорости потока.

Рис. 7.1. К выводу уравнения неразрывности (расхода)

Расход газа G кг/с – количество газа, проходящее через данное поперечное сечение канала (струи) в единицу времени, – равен:

G = F·c·ρ, (7.1)

где, F – площадь поперечного сечения канала;

с и ρ – скорость и плотность потока в этом сечении.

Уравнение неразрывности отражает следующую закономерность: при установившемся движении поток газа неразрывен, т.е. расход газа поступающего в рассматриваемый объём, равен расходу газа, выходящего из этого объёма:

G₁ = G₂.

Следовательно, при установившемся течении газа через любое сечение потока в единицу времени проходит одинаковая масса газа, т.е.

G₁ = G₂ = G = const

или

F·c·ρ = const. (7.2)

Уравнение (7.2) для рассматриваемых сечений 1-1 и 2-2 стационарного газового потока примет вид:

F₁·c₁·ρ₁ = F₂·c₂·ρ₂. (7.3)

Полученные уравнения (7.2) и (7.3) и есть уравнения неразрывности стационарного газового потока, устанавливающие связь между площадью поперечного сечения потока канала F, его скоростью c, и плотностью ρ в этом сечении. В этих уравнениях учитывается свойство сжимаемости газа.

В случае движения жидкости или несжимаемого потока газа, для которых ρ₁ = ρ₂ = ρ = const уравнение (7.3) приводится к виду:

F₁·c₁ = F₂·c₂. (7.5)

Из уравнения (7.5) следует, что при установившемся течении жидкости и несжимаемого потока газа скорость потока изменяется обратно пропорционально площади сечения канала.

Выполнив логарифмирование и последующее дифференцирование уравнения (7.2), получим уравнение неразрывности в дифференциальной форме:

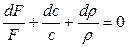(7.6)

или

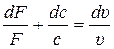. (7.7)

Если стенки канала проницаемые и через них может проникать газ, то условие (7.2) не выполняется. В этом случае уравнение неразрывности в дифференциальной форме имеет вид:

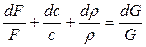, (7.8)

где dG – изменение расхода газа на элементарной длине канала.

Для произвольного сечения потока, составляющего угол α с направлением нормали к вектору скорости, расход определится так:

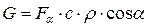, (7.9)

где F_α – площадь сечения, составляющего угол α с направлением нормали к вектору скорости (рис. 7.1.).

7.3. Уравнение первого закона термодинамики

Во второй теме было показано, что уравнение первого закона термодинамики (2.39) определяет баланс между теплом, подведённым к телу (или отведённым от него), изменением внутренней энергии и работой расширения (сжатия), т.е. работой изменения объёма. Поэтому уравнение первого закона термодинамики (2.41) применим и для потока газа:

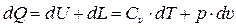. (7.10)

Уравнение (7.10) является общим, приложимым к любым газовым потокам, в том числе и нестационарным.

Если dυ = 0, то

.

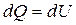Следовательно, если в потоке не совершается работа изменения объёма (p·dυ =0), то все тепло, подведённое (или отведённое) к газу, идет на изменение его внутренней энергии.

Из сказанного следует, что тепловая форма энергии (внутренняя энергия; энергия, подводимая в виде тепла) в потоке, так же, как и в неподвижной среде, может быть преобразована в механическую форму лишь посредством изменения объёма газа.

В том случае, когда рабочее тело несжимаемо (несжимаемая жидкость, dυ =0), тепло, подводимое к нему, не может быть преобразовано в какой-либо вид энергии механического движения (кинетическая энергия, потенциальная энергия и др.); оно только, как отмечалось, изменит внутреннюю энергию. Поэтому, например, несжимаемая жидкость не может служить рабочим телом тепловых двигателей.

Для движущегося газа удобно вместо внутренней энергии пользоваться понятием «энтальпия». Тогда воспользовавшись уравнением (2.44) получим другую форму записи уравнения первого закона термодинамики:

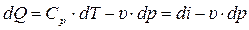. (7.11)

Чтобы перейти к интегральной форме уравнения первого закона термодинамики, выделим в потоке газа частицу, которая в начальный момент времени находится в сечении 1-1, и проследим изменение термодинамического состояния этой частицы газа за конечный промежуток времени, в течение которого она переместится в сечение 2-2 (рис. 7.2,а). В процессе движения выделенной частицы газа происходит её деформация, т.е. она находится в термодинамическом процессе изменения состояния. Это может быть процесс сжатия или расширения. Изобразим его в “p-υ” координатах линией процесса 1-2 (рис. 7.2,б). Интегрируя уравнение (7.11) от начального сечения 1-1 до конечного сечения 2-2 (рис. 7.2,а), считая течение одномерным и относя его величины к 1 кг воздуха, получим уравнение первого закона термодинамики для движущегося газа в интегральной форме

. (7.11')

В этом уравнении Q – все тепло, которое подводится к газу между сечениями 1-1 и 2-2. Оно состоит из тепла Q_внеш, подводимого к объёму газа извне, и того тепла Q_r, которое выделяется в результате работы сил трения.

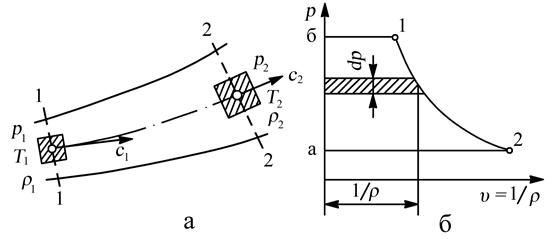Рис. 7.2. К составлению уравнения первого закона

термодинамики для движущегося потока

Следовательно,

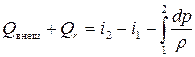(7.12)

В предположении, что тепло трения Q_r, эквивалентно работе сил трения (Q_r = L_r), получаем

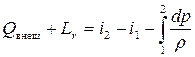(7.13)

Интеграл 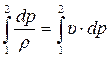представляет собой, как известно из техническойтермодинамики (формула 2.38), работу сжатия (расширения) движущегося газа. Процесс изменения состояния газа в элементах ГТД принято считать политропным и определять указанную работу по выражению

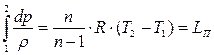. (7.14)

Эта работа численно равна площади aб12 (рис. 7.2,б).

7.4. Уравнение сохранения энергии

Чтобы получить уравнение сохранения энергии газового потока необходимо выяснить, какими видами энергии обладает движущийся газ. Каждый килограмм движущегося газа обладает следующими видами энергии:

а) внутренней энергией, равной 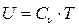, Дж/кг;

б) кинетической энергией, равной 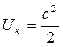, Дж/кг;

в) энергией давления (проталкивания) 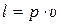, Дж/кг.

Энергия давления (энергия проталкивания) имеет смысл для открытой термодинамической системы, т.е. для движущегося газа. Она характеризует способность газа перемещаться из области с одним давлением в область с другим давлением.

Энергия давления измеряется работой, совершаемой силами давления газа при его движении.

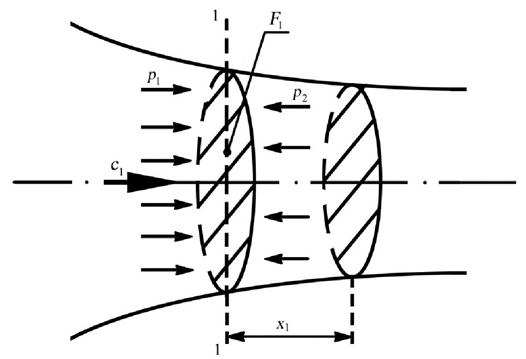
Чтобы получить формулу для вычисления энергии давления, найдём работу сил давления, которая затрачивается на проталкивание 1 кг газа через сечение 1–1 (рис. 7.3.).

С обеих сторон рассматриваемого сечения на газ действует сила

P₁= p₁·F₁,

где p₁ – давление;

F₁ – площадь поперечного сечения.

Для перемещения газа из сечения 1–1 на расстояние x₁ необходимо преодолеть силу P₁, совершив работу по перемещению массы газа, равную

L = P₁·x₁ = p₁·F₁·x₁,

где произведение F₁·x₁ представляет собой объём 1 кг газа (удельный объём υ) прошедшего через сечение 1–1, тогда

L = p₁·υ₁.

Рис. 7.3. К выводу формулы энергии давления

Величина, равная произведению давления газа на его удельный объём – p·υ представляет собой энергию (работу) проталкивания или энергию давления. Таким образом, каждый килограмм движущегося газа обладает кроме собственной внутренней энергии ещё и переносимой им энергией проталкивания, которую он получает от внешнего источника.

Уравнение сохранения энергии есть частное выражение всеобщего закона сохранения и превращения энергии, записанного применительно к газовому потоку, протекающему через какой–либо из элементов двигателя (рис. 7.4.), в котором в общем случае поток газа может получать или отдавать энергию. Поскольку при установившемся движении газа его расход через сечения 1-1 на входе и 2-2 на выходе одинаков, все входящие в уравнение сохранения энергии члены принято относить к 1 кг газа. Внешняя энергия может сообщаться (отводиться) газу как в форме механической работы L_внеш, так и в форме тепла Q_внеш.

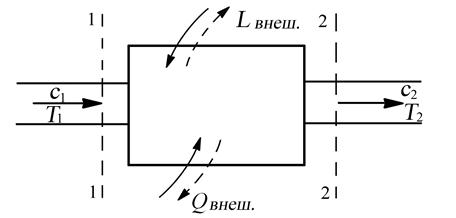
Рис. 7.4. К составлению уравнения сохранения энергии

Согласно закону сохранения энергии полная энергия газового потока на выходе из рассматриваемого элемента 2-2 будет больше (или меньше) полной энергии на входе в него 1-1 на величину сообщённой (отведённой) энергии между рассматриваемыми сечениями.

Так как полная энергия газового потока в каждом сечении равна сумме внутренней энергии, энергии давления и кинетической энергии, согласно сказанному, запишем уравнение сохранения энергии в общем виде

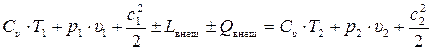. (7.15)

Уравнение (7.15) для упрощения расчётов приведём к другому виду, заменив сумму внутренней энергии и энергии давления энтальпией.

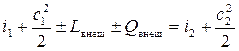. (7.16)

Для энергоизолированного газового потока (L_внеш = 0, Q_внеш = 0), уравнение сохранения энергии примет вид:

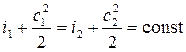. (7.17)

Уравнение (7.17) показывает, что при отсутствии энергообмена полная энергия газового потока в любом сечении элемента двигателя, равная сумме энтальпии и кинетической энергии, сохраняется неизменной.

Важно отметить, что уравнения (7.16), (7.17) не содержат в явном виде гидравлических потерь, учитываемых в виде работы от сил гидравлических сопротивлений L_r. Они имеют совершенно одинаковый вид, как при отсутствии, так и при наличии гидравлических потерь. Силы гидравлического сопротивления (условно называемые также силами трения) возникают из-за наличия трения, вихреобразования и волнового сопротивления. Для рассматриваемой системы они являются внутренними силами, а работа, затрачиваемая на их преодоление, переходит практически полностью в тепло (L_r = Q_r).

Если же часть этого тепла уходит через стенки наружу, оно должно быть учтено в величине Q_внеш. Поэтому наличие гидравлических потерь приводит только к преобразованию одного вида энергии другой и не отражается на общем балансе энергии. Из уравнения (7.16) следует, что если наличие гидравлических потерь приводит к уменьшению кинетической энергии газа в сечении 2-2, то ровно на столько же увеличивается энтальпия газа в этом сечении. Таким образом, уравнения (7.16), (7.17) справедливы для установившегося течения вязкого сжимаемого газа. В каждом конкретном случае могут быть различными только направление внешнего воздействия (подвод или отвод) и вид подводимой или отводимой энергии.

Уравнение (7.16) запишем в другой форме, где слева будет отражено полное количество энергии подводимой к газу, которое складывается из теплоты подведённой к газу (Q_внеш) и работы внешних сил подведённой к газу (-L_внеш), а справа результат изменения энергии газового потока.

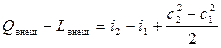. (7.18)

или в дифференциальной форме

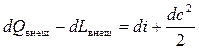. (7.19)

Уравнение сохранения энергии в форме (7.18) можно сформулировать так: внешняя энергия, подведённая к потоку газа в виде тепла и работы, идёт на изменение энтальпии и кинетической энергии газа.

В случае идеального газа

.

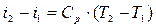Поэтому для идеального газа уравнение (7.18) можно представить в виде

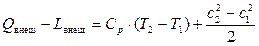. (7.20)

или в дифференциальной форме

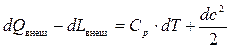. (7.21)

Таким образом, полученные уравнения неразрывности (расхода) и уравнение сохранения энергии, являются важнейшими уравнениями термодинамики, позволяющие выполнить газодинамический расчёт как элементов ГТД, так и двигателя в целом.

7.5. Применение уравнения сохранения энергии и уравнения

неразрывности к элементам ГТД

7.5.1. Рассмотрим применение закона сохранения энергии для элементов ГТД. Обозначения сечений будем принимать такими, как показано на рис. 7.5.

Используя уравнение сохранения энергии (7.16) всегда можно найти закономерности движения газа в любом элементе ГТД. Приведём примеры использования уравнения (7.16) для расчётов элементов ГТД.

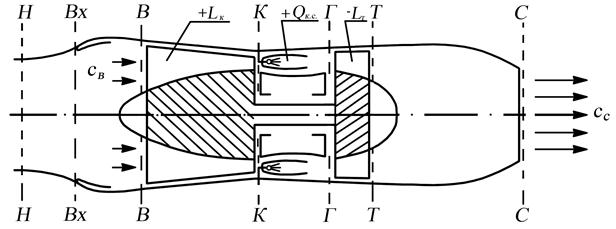
Рис. 7.5. Схема ТРД и обозначение основных сечений

1. Для процесса движения воздуха через входное устройство Q_внеш= 0 и L_внеш= 0, поэтому уравнение (7.16) будет иметь вид

,

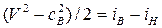где V – скорость полета.

Таким образом, во входном устройстве в полёте кинетическая энергия воздуха преобразуется в его энтальпию. В результате увеличиваются температура и давление воздуха, а скорость потока снижается.

2. При движении воздуха через компрессор ГТД с достаточной для практики точностью можно считать, что Q_внеш= 0. Тогда уравнение (7.16) принимает вид

,

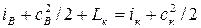где L_к = L_внеш – механическая работа, переданная 1 кг воздуха лопатками рабочего колеса компрессора.

Обычно компрессор выполняют так, что скорость воздуха на выходе и входе примерно одинакова (c_к ≈ c_в), следовательно,

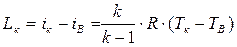. (7.22)

Отсюда видно, что механическая работа компрессора затрачивается на увеличение энтальпии воздуха, в результате повышаются его давление и температура.

Реальный процесс сжатия воздуха в компрессоре ГТД оказывается политропным, так как при сжатии необходимо преодолеть силы трения, а выделившееся при этом тепло подводится к воздуху.

С учётом сказанного и после простых преобразований, применив уравнение (3.49), уравнение (7.22) можно представить в следующем виде:

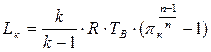(7.23)

где 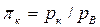– степень повышения давления воздуха в компрессоре.

Из этого выражения следует, что механическая работа, подведённая к каждому килограмму воздуха в компрессоре, зависит от температуры воздуха на входе в компрессор Т_в, степени повышения давления π_к и показателя политропы n.

Если рассматривать идеальный компрессор, в котором отсутствует теплообмен и силы трения, процесс сжатия будет адиабатным. Работа компрессора в этом случае называется адиабатной и определяется по формуле

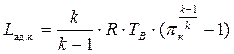. (7.24)

Уравнения (7.22) и (7.23) могут быть использованы для определения L_к по измеренным или вычисленными значениями Т_к и Т_в. Зная работу L_к, можно найти мощность N_к, потребную для вращения компрессора:

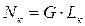. (7.25)

3. Для процесса движения потока через камеру сгорания (рис. 7.5.) L_внеш = 0; Q_внеш = Q_к.с., поэтому уравнение (7.16) примет вид:

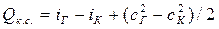, (7.26)

где Q_к.с. – теплота, теплота подводимая к 1 кг воздуха в камере сгорания.

Из выражения (7.26) видно, что теплота, подведённая к воздуху в камере сгорания ГТД, расходуется на увеличение его энтальпии и кинетической энергии.

4. При движении газов через турбину ГТД можно считать, что Q_внеш = 0. Тогда уравнение (7.16) примет такой вид:

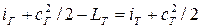, (7.27)

где L_Т = L_внеш– механическая работа, полученная на рабочем колесе турбины от 1 кг газа.

В турбине реальный процесс расширения также оказывается не адиабатным, а политропным вследствие наличия сил трения.

Уравнение (7.27) позволяет найти механическую работу турбины. После ряда преобразований получим

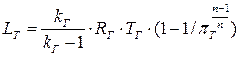, (7.28)

где 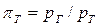– степень понижения давления газа в турбине.

Из формулы (7.28) следует, что механическая работа, получаемая в турбине, зависит от температуры Т_Г перед турбиной, степени понижения давления π_Т и показателя политропы n.

При отсутствии сил трения и внешнего теплообмена процесс движения газа через турбину будет адиабатным. Работа турбины в этом случае называется адиабатной и определяется по формуле

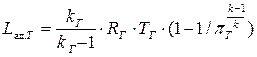. (7.29)

Зная величину работы, полученной на рабочем колесе турбины L_Т и расход газа G_Г, можно определить мощность N_Т, развиваемую газовой турбиной, используя формулу (7.28), в которой обычно всегда известны температура газов Т_Г и степень понижения давления газа в турбине π_Т:

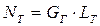. (7.30)

5. Для процесса движения газа через выходное устройство ГТД (рис. 7.5.) Q_внеш = 0 и L_внеш = 0, поэтому уравнение (7.16) будет иметь вид

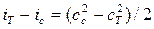, (7.31)

т.е. в выходном устройстве происходит преобразование энтальпии в кинетическую энергию газового потока (давление и температура при этом уменьшаются, а скорость растёт).

6. Если рассмотреть движение потока через весь двигатель (рис. 7.5.), получим

.

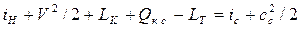Так как в ГТД L_Т ≈ L_к.

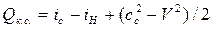. (7.32)

Анализируя уравнение (7.32), можно сделать вывод, что в результате процессов, происходящих в ГТД, изменяется энтальпия рабочего тела и тепловая энергия, подводимая к воздуху в камере сгорания, преобразуется в кинетическую энергиию потока.

7.5.2. Применение уравнения неразрывности к элементам ГТД

При установившемся течении рабочего тела (на установившихся режимах работы ГТД) расход в каждом сечении газовоздушного тракта остается неизменным и равен произведению площади этого сечения, средней скорости потока и плотности, то есть:

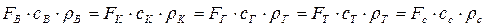, (7.33)

где индексы при переменных соответствуют сечениям проточной части двигателя (рис. 7.5.).

7.6. Обобщенное уравнение Бернулли

При расчёте элементов ГТД важно знать энергию газового потока, затраченную на преодоление сил трения, так как она определяет КПД элементов и двигателя в целом. Определить работу трения можно с помощью обобщённого уравнения Бернулли.

Обобщённое уравнение Бернулли получается из совместного решения уравнений сохранения энергии (7.16), и первого закона термодинамики (7.13) вычитая из (7.16) уравнение (7.13), получаем

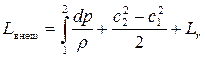(7.34)

или

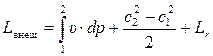. (7.34')

Эти уравнения показывают, что внешняя работа, подводимая к газу или отводимая от него, затрачивается на совершение политропной работы, изменение кинетической энергии и преодоление гидравлических потерь на рассматриваемом участке проточной части двигателя между сечениями 1-1 и 2-2.

Запишем уравнение (7.34') в дифференциальном виде

dL_внешн. = υ·dp + 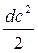+ dL_r . (7.35)

При течении газа в каналах без подвода внешней работы (L_внешн = 0) и без трения (L_r = 0), то уравнение (7.35) примет вид:

– υ·dp = c·dc. (7.36)

Из последнего выражения следует, что в таком потоке разгон газа (dc > 0) возможен лишь при понижении его давления (dp < 0), а торможение (dc < 0) сопровождается ростом давления (dp > 0). Наличие трения, естественно, сказывается количественно на параметрах потока. Например, при заданном уровне понижения давления наличие трения (L_r > 0) понизит прирост скорости потока, и, наоборот, в случае торможения потока при заданном уровне понижения скорости при наличии трения, давление будет возрастать в меньшей степени, чем без трения.

В уравнение (7.34) входят только механические величины, поэтому его можно рассматривать, как уравнение сохранения энергии в механической форме. Но хотя в обобщённое уравнение Бернулли не входит в явном виде внешнее тепло, оно применимо как для процессов с теплообменом, так и без него. Интенсивность и направление подвода внешнего тепла косвенно учитываются в численных значениях отдельных величин, входящих в уравнение (7.34). Заметим, что поскольку уравнение (7.34) получено из уравнений (7.13) и (7.16), то эти уравнения не могут рассматриваться как независимые, но два любые из них могут приниматься в качестве независимых.

Обобщённое уравнение Бернулли позволяет оценить баланс механических видов энергии при движении газа в любом элементе ГТД.

7.6.1. Рассмотрим примеры записи обобщённого уравнения Бернулли для элементов двигателя (рис. 7.5.).

1. При течении воздуха через входное устройство L_внеш = 0, L_r = L_{r вх.у} , поэтому уравнение Бернулли будет иметь вид

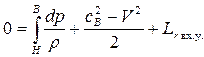(7.37)

или

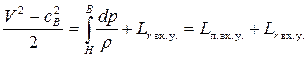, (7.38)

где V – скорость полета; c_в – скорость потока за входным устройством.

Из уравнения (7.38) видно, что изменение кинетической энергии расходуется на совершение политропной работы сжатия и преодоления сил трения. В результате кинетическая энергия потока уменьшается, а давление и температура воздуха увеличиваются.

2. Для компрессора L_внеш = L_к; L_r = L_{r к}, поэтому

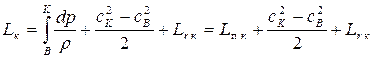, (7.39)

где

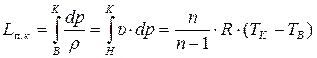. (7.40)

В “p-υ” координатах политропная работа сжатия воздуха в компрессоре L_п.к равна площади в'вкк', рис 7.6,а.

Физический смысл уравнения (7.39) состоит в том, что внешняя работа, сообщаемая воздуху в теплоизолированном компрессоре (Q_к = 0), расходуется на политропное сжатие воздуха, изменение его кинетической энергии и на преодоление гидравлических потерь.

3. Для всего процесса сжатия воздуха в двигателе от сечения Н-Н до сечения К-К (рис. 7.5.) уравнение Бернулли дает

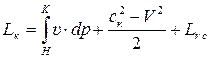, (7.41)

где 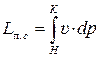–суммарная политропная работа сжатия (во входномустройстве и компрессоре), равная площади Н'К'КНН' (рис. 7.6,г).

4. Для камеры сгорания L_внеш = 0; L_r = L_{r к.с} , поэтому

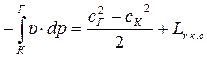. (7.42)

Как видно из “p-υ”диаграммы, реальный процесс подвода тепла в камере сгорания сопровождается расширением газа. Работа расширения расходуется на увеличение кинетической энергии (с_Г > с_К) и на преодоление гидравлических потерь (рис. 7.6, в).

5. Для турбины L_внеш = – L_T ; L_r = L_{r Т}, поэтому

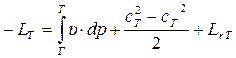, (7.43)

и, следовательно,

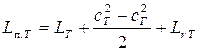, (7.44)

где политропная работа турбины 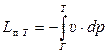и в “p-υ” координатах равна площади Т'ТГГ' (рис. 7.6,б).

В данном случае располагаемой работой является политропная работа, которую совершает сжатый и нагретый газ при расширении в турбине. Эта работа расходуется на получение полезной работы на валу турбины, приращение кинетической энергии газового потока и преодоление гидравлических потерь в проточной части турбины.

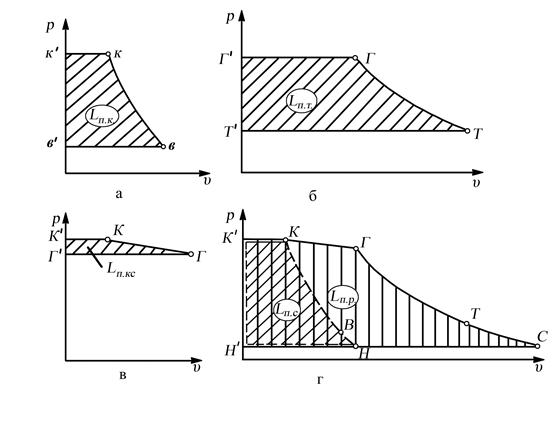
Рис. 7.6. Изображение процессов ГТД в “p–υ” координатах

6. При течении газа через выходное устройство L_внеш = 0; L_r = L_{r вых. у}, поэтому уравнение Бернулли будет иметь вид

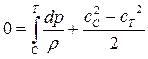+ L_{rвых. у.} (7.45)

так как в выходном устройстве происходит расширение газа, L_п.вых.у > 0. Следовательно,

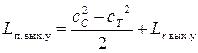(7.46)

т.е. политропная работа расширения газа расходуется на увеличение кинетической энергии потока и преодоление трения.

7. Для всего процесса расширения газового потока в двигателе от сечения К-К до сечения С-С (рис. 7.5.)

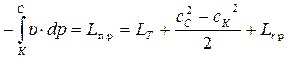. (7.47)

Здесь L_п.р – суммарная политропная работа расширения в камере сгорания, турбине и реактивном сопле, равная площади Н'К'КГТСН' (рис. 7.6,г).

В заключение отметим, что рассматриваемые уравнения движения используются в предположении, что газ является совершенным, т.е. подчиняется уравнению состояния в виде 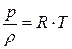или p∙υ = R∙T.

Основными параметрами, характеризующими движение газа, являются с, ρ, р,и Т. Для получения замкнутой системы уравнений относительно этих параметров имеются четыре уравнения: уравнение неразрывности, уравнение состояния и любые два из трех указанных энергетических уравнений.

Типы решаемых задач могут быть различными. Если, например, известны параметры газового потока на входе в рассматриваемый элемент двигателя и заданы для этого элемента величины L_внеш , Q_внеш и L_r , то составленная указанным образом система уравнений позволяет определить параметры газа на выходе из этого элемента. Может рассматриваться задача определения по заданным параметрам на входе и выходе величин L_внеш , Q_внеш и L_r и т.п.

7.6.2. Уравнение Бернулли для жидкости и несжимаемого газа

При отсутствии внешней работы (L_внеш = 0) и трения (L_r = 0) для жидкости и несжимаемого газа (ρ = const) уравнение (7.34) имеет вид

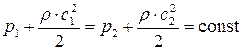, (7.48)

где p₁, p₂– действительные (статические) давления в рассматриваемых сечениях;

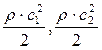– динамические давления (скоростные напоры) в соответствующих сечениях потока.

Уравнение (7.48) позволяет сделать вывод, что сумма статического и динамического давлений при течении жидкости и несжимаемого газа без подвода внешней работы и отсутствии трения, остается неизменным.

Сумму статического и динамического давлений называют полным давлением заторможенного потока и обозначают:

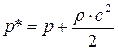. (7.49)

С учётом (7.47) уравнение (7.46) можно записать так:

.

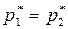Иначе говоря, при течении энергоизолированного потока жидкости и несжимаемого газа и отсутствии трения, полное давление остаётся неизменным (p* = const). Уравнение Бернулли в форме (7.49) используется для определения скорости жидкости и газа (при М ≤ 0,4…0,6). Статическое давление измеряют трубкой а (рис. 7.7.), в которой измерительная плоскость параллельна вектору скорости. Полное давление измеряют Г-образной трубкой б (рис. 7.7.), в которой измерительная плоскость поставлена перпендикулярно вектору скорости.

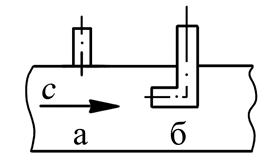Рис. 7.7. Схема датчиков для измерения статического (а) и

полного (б) давлений

7.7. Уравнение Эйлера о количестве движения

Уравнение количества движения в механике получают как следствие второго закона Ньютона.

Если за малый промежуток времени Δτ на тело массой т действует сила P, то тело получит ускорение равное 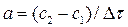, где с – скорость тела.

Тогда

,

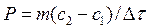или

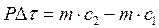. (7.50)

Произведение тс называют количеством движения тела, или импульсом тела, а PΔτ – импульсом силы. Из уравнения (7.50) следует, что изменение количества движения тела равно импульсу силы. Эта известная из физики теорема об изменении количества движения.

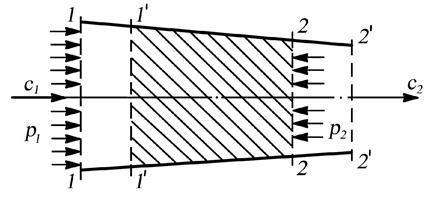Применим эту теорему к установившемуся течению газа по прямолинейному каналу (рис. 7.8.). Выделим некоторый объём газа контрольной поверхностью, которая состоит из поперечных сечений 1-1 и 2-2 и боковой поверхности, прилегающей к стенкам канала. На выделенный объём газа действуют силы давления, втекающего (в сечении 1-1) и вытекающего (в сечении 2-2) потока, а также силы давления и трения о стороны стенок канала. Сумма импульсов этих сил равна ΣPΔτ.

Рис. 7.8. К выводу уравнения Эйлера о количестве движения

Найдем изменение количества движения массы газа Δ(mc), заключённого в выделенном объёме. За малый промежуток времени Δτ выделенная масса газа переместится из положения 1-2 в положение 1'-2'. При установившемся движении потока количество движения массы газа, заключённого между сечениями 1'-1' и 2-2, не изменится. Следовательно, изменение количества движения всей рассматриваемой массы газа определится изменением количества движения элементарных масс, находящихся в объёмах 1-1' и 2-2', т.е.

.

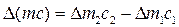Умножим и разделим правую часть равенства на Δτ. Получим

.

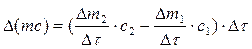Учитывая, что 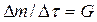– секундный массовый расход и G₁ = G₂ = G = const в соответствии с уравнением неразрывности (7.2), то изменение количества движения определяется по формуле:

.

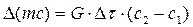В соответствии с уравнением (7.50) получим

,

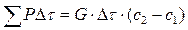или

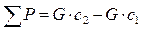. (7.51)

Это уравнение впервые было получено Л. Эйлером в 1755 г. и поэтому носит его имя.

Согласно уравнению Эйлера при установившемся движении газа сумма всех внешних сил, действующих на массу газа, выделенную контрольной поверхностью, равна разности количеств движения секундной массы газа, вытекающей и втекающей через контрольную поверхность. Важность уравнения Эйлера состоит в том, что с его помощью можно определить газодинамические силы, действующие на различные элементы ГТД, не вдаваясь в сущность явлений, происходящих внутри выделенного объёма. Для определения этих сил важно знать лишь данные параметров газа на контрольной поверхности. С помощью уравнения Эйлера можно получить выражение силы тяги реактивного двигателя, сил, действующих на лопатки компрессора и турбины и др.

В заключении отметим лишь, что именно с использованием уравнения (7.51) академиком Б.С. Стечкиным еще в 1929 году была получена формула тяги ВРД, носящая в настоящее время его имя.

Формула для тяги ВРД академика Б.С. Стечкина имеет вид:

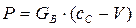, (7.52)

где P – тяга ВРД;

G_В – расход воздуха;

c_c – скорость истечения газов из сопла;

V – скорость летательного аппарата.

Вывод этой формулы будет рассмотрен в теории авиационных двигателей.

7.8. Уравнение Эйлера о моменте количества движения

При изучении вращательных движений газа следует использовать ещё один из законов механики – закон об изменении момента количества движения, который гласит: изменение момента количества движения тела равно моменту импульса равнодействующей всех внешних сил, приложенных к телу. Напомним, что моментом количества движения (М) тела относительно некоторой точки, называется произведение количества движения тела (m·c) на кратчайшее расстояние (r) от точки до линии, по которой направлена скорость тела, то есть M = (m·c·r). Моментом импульса называется произведение величины импульса (PΔτ) на кратчайшее расстояние (r) от точки до линии действия силы, создающий импульс.

Найдём уравнение моментов количества движения для случая, когда телом является газ, движущийся в некотором канале (рис. 7.9.).

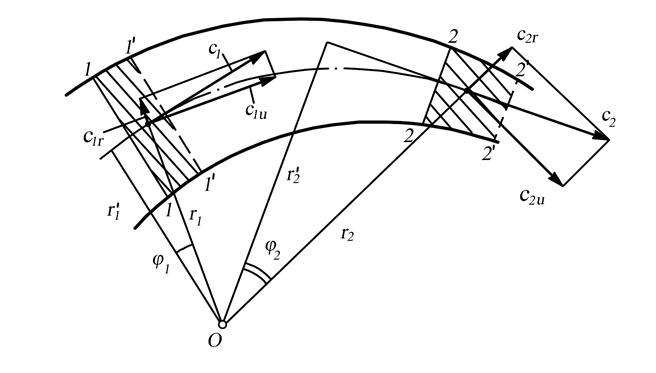
Рис. 7.9. К выводу уравнения Эйлера

о моменте количества движения

Как и ранее, будем рассматривать изменение состояния выделенного сечениями 1-1 и 2-2 объёма за малый промежуток времени Δτ, а движение будем считать установившимся. Изменение момента количества движения будет равно разности моментов количества движения объемов 2-2' и 1-1'.

Момент количества движения объёма 1-1' равен 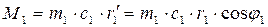, а из (рис. 7.8.) видно, что произведение 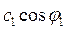, есть не что иное, как окружная составляющая скорости с₁:

.

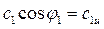Таким образом, момент количества движения объема 1-1' равен

.

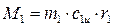Аналогично этому момент количества движения объема 2-2' равен

.

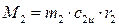Разность между этими величинами нужно приравнять моменту импульса равнодействующей

,

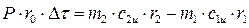где P – равнодействующая внешних сил;

r_о– расстояние от линии действия силы P до оси О.

При установившемся движении массы объёмов 1-1' и 2-2' одинаковы. Учитывая, что 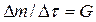– секундный массовый расход и G₁ = G₂ = G = const в соответствии с уравнением неразрывности, а произведение P · r_о даёт момент равнодействующей P относительно точки O: P · r_о = M.

Окончательно уравнение моментов количества движения для потока газа имеет вид:

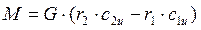(7.53)

Уравнение (7.53) называется также уравнением Эйлера для вращательного движения. Оно позволяет вычислить момент сил, действующих со стороны газа на тела, взаимодействующие с потоком газа.

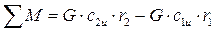(7.54)

Согласно этому уравнению, при установившемся течении газа и отсутствии массовых сил, сумма моментов внешних сил, действующих на выделенную массу газа со стороны обтекаемых тел и контрольной поверхности относительно произвольной оси, равна разности моментов относительно той же оси окружных составляющих количеств движения секундных масс газа, вытекающих и втекающих через рассматриваемую контрольную поверхность.

Используем уравнение (7.54) для того, чтобы вычислить момент, действующий на колесо газового компрессора. Колесо воздействует на газ в то время, когда газ находится между входным 1 и выходным 2 сечениями (рис. 7.10.).

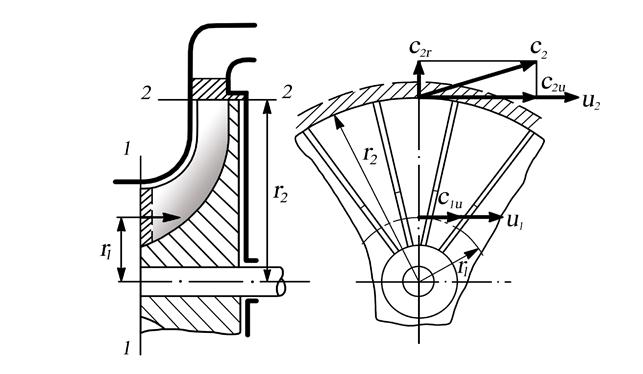Рис. 7.10. Схема рабочего колеса центробежного компрессора

К сечению 1-1 газ может подходить с некоторой окружной скоростью, которая сообщается ему во входном направляющем аппарате. Значение этой окружной скорости на среднем радиусе r₁ входного сечения 1-1 обозначим с_1u. Тогда уравнение (7.53) дает значение крутящего момента, необходимого для вращения рабочего колеса. Умножив момент на угловую скорость вращения, можно вычислить теоретическую мощность, необходимую для привода компрессора:

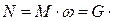
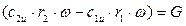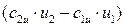· Вт, (7.55)

где u₁и u₂ – окружные скорости колеса на радиусах r₁ и r₂. К этой мощности следует ещё добавить мощность, расходуемую на преодоление трения колеса о газ за пределами участка 1-2 и на преодоление трения в подшипниках.

Из уравнений (7.54) и (7.55) легко определяется внешняя механическая работа L_внеш, подводимая к единице массы газа (или отводимая от неё) в рабочем колесе ступени компрессора (турбины), выраженная через параметры газа:

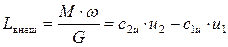, Дж/кг. (7.56)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 7.1.

Определить температуру воздушного потока на входе в двигатель, если известно, что самолёт совершает полёт на высоте 10,5 км со скоростью 900 км/ч, а скорость потока на входе в двигатель 200 м/с.

Решение

При полёте самолёта скорость набегающего потока в сечении Н-Н (рис. 7.5.) равна скорости полета самолета 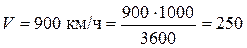м/с. Такимобразом, на участке Н-Н и Вх-Вхпроисходит уменьшение скорости воздуха относительно двигателя. Это торможение потока происходит практически без потерь на трение и без теплообмена с соседними струями потока, и процесс торможения можно считать адиабатным.

Для расчёта температуры T_вх в сечении Вх–Вх (на входе в двигатель) используем уравнение (7.16), учитывая, что на участке между сечениями Н-Н и Вх-Вх величины L_внеш = 0 и Q_внеш = 0, а температура в сечении Н-Н равна температуре окружающего воздуха. По заданной высоте полета Н = 10,5 км в таблице стандартной атмосферы (ГОСТ 4401-81) находится температура Т_Н = 220 К.

Уравнение (7.16) с учётом вышесказанного будет иметь вид:

.

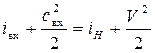После преобразований получим окончательную формулу для вычисления температуры Т_вх

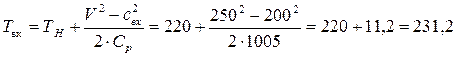К.

Таким образом, при торможении потока его температура повысится на 11,2 К, и воздушный поток на входе в двигатель в сечении Вх-Вх будет иметь температуру 231,2 К.

Проверим правильность получения размерности температуры:

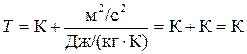, так как размерность 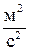эквивалентна размерности .

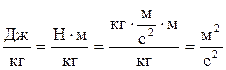Задача 7.2.

При движении энергоизолированного потока газа по каналу на определённом участке его кинетическая энергия увеличилась на 60 300 Дж/кг. Определить, как и на сколько изменилась температура газа.

Решение

Воспользуемся формулой (7.17) уравнением сохранения энергии для энергоизолированного потока и запишем его для произвольных сечений канала 1-1 и 2-2, между которыми произошло увеличение кинетической энергии.

.

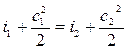Для поиска искомой величины ΔТ проведём преобразования и получим:

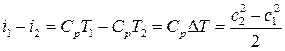
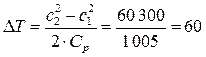К.

Таким образом, температура газа понизится на 60 К, так как часть внутренней энергии газа затрачивается на увеличение кинетической энергии.

Проверим правильность получения размерности изменения температуры ΔТ.

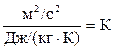, так как размерность 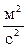эквивалентна размерности 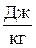(смотри задачу 7.1.).

Задача 7.3.

Определить расход газа на выходе из реактивного сопла, если известны с_с = 300 м/с; ρ_с = 0,25 кг/м³; и F_с = 1 м².

Решение

Воспользуемся уравнением (7.1) для определения расхода газа

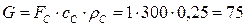кг/с.

Таким образом, расход газа из реактивного сопла площадью поперечного сечения в 1 м², при скорости истечения газа 300 м/с и плотности этого газа 0,25 кг/м³ составляет 75 кг/с.

Задача 7.4.

Определить механическую работу L_Т, полученную на рабочем колесе турбины от 1 кг газа, если известны температура газов Т_Г = 1 300 К и скорость газа с_Г = 100 м/с на входе в турбину, а также температура Т_с = 300 К и скорость с_с = 1 100м/с на выходе из сопла.

Решение

Составим уравнение сохранения энергии (7.16) для сечений Г-Г и С-С (рис. 7.5.). Для решения задачи учтём, что L_внеш = – L_Т, Q_внеш = 0 и уравнение примет вид:

.

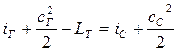Принимая во внимание, что 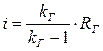и выполнив несложные преобразования, получим формулу для вычисления L_Т :

,

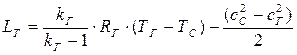где k_Г = 1,33 – коэффициент адиабаты для газов;

R_Г = 288 Дж/(кг·К) – газовая постоянная для продуктов сгорания.

Используя исходные данные, окончательно получим численное значение L_Т

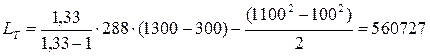Дж/кг.

Таким образом, механическая работа L_Т, полученная на рабочем колесе турбины от каждого килограмма газа равна L_Т = 560727 Дж/кг.

Задача 7.5.

Определить силу, действующую на выходное устройство TPД (рис. 7.11.), если дано: p_Т = 1,94 кгс/см²; с_Т = 300 м/с; F_Т = 1850 см²; p_С = 1,16 кгс/см²; с_С = 550 м/с и F_C = 1500 см². Секундный расход газа составляет 50 кг/с.

Решение

Применим к выходному устройству уравнение Эйлера о количестве движения (7.51), считая направление движения газа положительным:

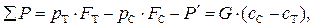
где p_Т ∙ F_Т – силы давления втекающего потока;

p_С ∙ F_C – силы давления вытекающего потока;

P' – сила воздействия выходного устройства на поток, ограниченный сечениями Т-Т и С-С. (P' является результирующей сил давления и трения, действующей на газ со стороны стенок канала).

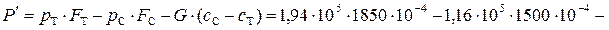
– 50 ∙ (550 – 300)=35890 – 17400 – 12500 = 5990 Н = 5,6 кН.

На выходное устройство TPД действует в соответствии с третьим законом Ньютона газовая сила, равная P = – P' = 5,6 кН и направленная по потоку.

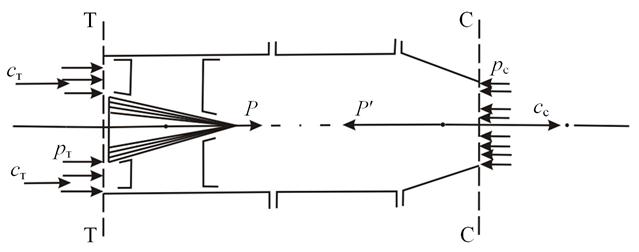
Рис. 7.11. К определению газовой силы, действующей на выходное устройство ТРД

Задача 7.6.

Определить газовую силу, действующую на лопатки соплового аппарата (СА) турбины (рис. 7.12.), если дано p_Г = 7 кгс/см²; с_Г = 150 м/с; F_Г = F_СА = 40 см²; p_СА = 4,83 кг/см²; с_СА = 490 м/с; α_СА = 24º. Секундный расход газа через один лопаточный канал равен G_Г = 1,2 кг/с.

Решение

Обратимся к рис. 7.12., где изображены все силы, действующие со стороны лопаточного канала на поток газа и газовые силы, действующие на лопатку соплового аппарата.

Воспользуемся уравнением Эйлера (7.51). В проекции на осевое направление уравнение Эйлера примет следующий вид:

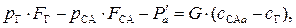
где 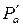– осевая составляющая силы воздействия лопаточного канала на поток газа, ограниченный сечениями Г-Г и СА-СА.

Откуда,

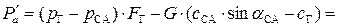
= (7∙10⁵ – 4,83∙10⁵) ∙ 40∙10^-4 – 1,2 ∙ (490 ∙ 0,407 – 150) = 809 Н.

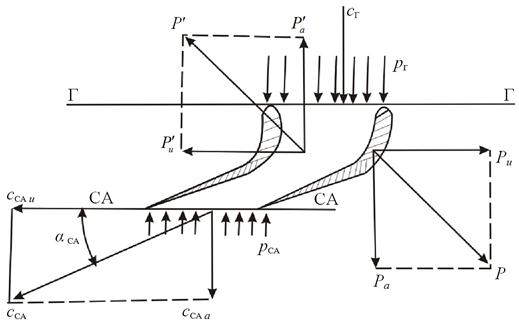
Рис. 7.12. К определению газовой силы, действующей на лопатку соплового аппарата турбины

В проекции на окружное направление уравнение Эйлера примет следующий вид:

,

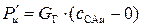где 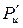– окружная составляющая силы воздействия лопаточного канала на поток газа ограниченный сечениями Г-Г и СА-СА.

Откуда,

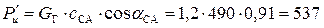Н.

Очевидно, что

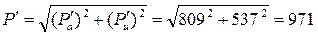Н.

Так как число лопаток равно числу каналов, то на каждую лопатку соплового аппарата действует сила P, равная по величине и противоположная по направлению найденной силе P'.

Таким образом, P = – P'= 971Н.

Задача 7.7.

Определить величину работы центробежного компрессора (рис. 7.10.) подводимой к единице массы воздуха, вычислить теоретическую мощность, необходимую для привода компрессора, если окружная скорость колеса на внешнем радиусе u₂ = 480 м/с; окружная скорость колеса на входе в компрессор u₁ = 250 м/с; окружные составляющие скоростей воздуха на входе в колесо с_1u = 50 м/с и на выходе из него с_2u = 450 м/с, а расход воздуха через компрессор составляет 10 кг/с.

Решение

С помощью уравнения (7.56) определим величину работы компрессора подводимой к каждому килограмму воздуха

L_К = с_2u ∙ u₂ – с_1u ∙ u₁ = 450 ∙ 480 – 50 ∙ 250 = 203500 Дж/кг.

Уравнение (7.55) позволяет вычислить теоретическую мощность, потребляемую центробежным компрессором.

N_К = G_В ∙ L_К = 10 ∙ 203500 = 2035000 Вт = 2035 кВт.

Проверьте, как Вы усвоили материал

1. Назовите основные допущения, которые принимаются при расчётах газовых потоков.

2. Какое течение газового потока считается стационарным (установившимся)? Приведите примеры.

3. Какими параметрами характеризуется движущийся газ?

4. Дайте определение массовому расходу воздуха.

5. Напишите и сформулируйте уравнение неразрывности для жидкости и газа.

6. Какими видами энергий обладает движущийся газ? Напишите формулы, определяющие величину каждого из этих видов энергии.

7. Напишите уравнение неразрывности в дифференциальной форме.

8. Напишите уравнение первого закона термодинамики для движущегося газа.

9. Как учитывается трение при расчёте элементов ГТД?

10. Напишите и сформулируйте уравнение сохранения энергии: а) в общем виде;

б) для энергоизолированного потока.

11. Напишите и сформулируйте уравнение сохранения энергии для движущегося потока в ТРД (рис. 7.5.): а) по входному устройству; б) по компрессору; в) по камере сгорания; г) по турбине; д) по выходному устройству.

12. Оказывает ли влияние на величину общего запаса энергии движущегося газа работа, затраченная на преодоление трения?

13. Напишите и сформулируйте обобщенное уравнение Бернулли.

14. Напишите и сформулируйте уравнение Бернулли для жидкости и несжимаемого потока газа.

15. В чём состоит различие между уравнением Бернулли и уравнением сохранения энергии?

16. Напишите уравнение Эйлера для поступательного и вращательного движения.

17. Как изменится скорость, статическое и динамическое давление жидкости и несжимаемого газа при изменении площади поперечного сечения потока?

Дата добавления: 2014-09-08; просмотров: 2882; Нарушение авторских прав

Мы поможем в написании ваших работ!