
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ТЕМА 8. ТЕРМОДИНАМИКА ГАЗОВОГО ПОТОКА
Течение газа (воздуха) в элементах летательных аппаратов и силовых установок происходит часто с изменением его скорости, т.е. с разгоном или торможением потока. Основные уравнения газового потока, рассмотренные в предыдущей теме 7, показывают, что изменение скорости газа всегда сопровождается изменением его основных параметров состояния. В общем случае эти изменения могут быть вызваны различными воздействиями, как, например, подводом или отводом тепла и работы, изменением площади проходного сечения канала и др. Анализ влияния этих воздействий на течение газа приводится далее.
8.1. Форма канала, необходимая для разгона и торможения
газового потока
Воздействие на газовый поток, связанное с изменением площади поперечного сечения канала F, называют обычно геометрическим воздействием. Рассмотрим, как необходимо изменять форму канала, по которому течёт газ, для того чтобы обеспечить его разгон или торможение за счёт геометрического воздействия. При этом будем считать газ идеальным, а его течение – происходящим без трения и энергообмена с окружающей средой (Qвнеш = Lвнеш = Lr = 0). Следовательно, процесс изменения состояния газа при этих условиях будет адиабатным.
Канал, в котором скорость потока газа увеличивается (dc > 0), называется соплом. Как видно из (7.35) и (7.17), при течении газа в сопле происходит снижение его давления (dp < 0), температуры (dT < 0) и плотности. Таким образом, при течении в сопле газ расширяется.
Канал, в котором происходит уменьшение скорости потока газа (dc < 0), называется диффузором. Торможение потока вызывает противоположное изменение параметров газа – возрастают давление (dp > 0), температура (dТ > 0) и плотность газа. При течении в диффузоре газ сжимается.
Получим уравнение профиля струи для энергоизолированного течения без трения.
Поскольку в энергоизолированном течении параметры потока связаны между собой уравнением адиабаты
pυk = const,
используем его в дифференциальном виде
υk ∙ dp + kυk-1 ∙ pdυ = 0
или
υdp + k ∙ pdυ = 0. (8.1)
Выражаем из (8.1) υ·dp и подставляем в уравнение Бернулли [сdc = – υdp (7.36)]. В результате получим:
c·dc = k ∙ pdυ
или
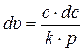 . (8.2)
. (8.2)
С учётом уравнения состояния pυ = RT выражение (8.2) можно записать в виде
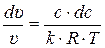 . (8.3)
. (8.3)
Учитывая, что kRT = a2, то (8.3) принимает вид:
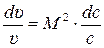 . (8.4)
. (8.4)
Используя уравнение неразрывности (7.7)
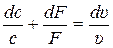 .
.
уравнение (8.4) примет вид:
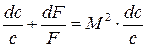
или
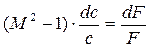 . (8.5)
. (8.5)
Выражение определяемое (8.5) и есть уравнение профиля струи для энергоизолированного потока без трения.
Уравнение (8.5) связывает величину dc, определяющую характер изменения скорости потока, с величиной dF, характеризующей изменение площади проходного сечения канала, т.е. его форму.
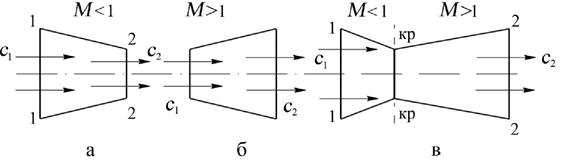
Рис. 8.1. Формы каналов для разгона потока
Форма сопла (dc > 0). Определим, какую форму может иметь канал, предназначенный для разгона потока. Если скорость потока на входе в сопло меньше скорости звука (М < 1), то величина ( 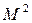 – 1) < 0. Уравнение (8.5) удовлетворяется в этом случае при dF < 0. Таким образом, для разгона дозвукового потока канал должен быть суживающимся (рис. 8.1,а)
– 1) < 0. Уравнение (8.5) удовлетворяется в этом случае при dF < 0. Таким образом, для разгона дозвукового потока канал должен быть суживающимся (рис. 8.1,а)
Если на входе в сопло скорость потока сверхзвуковая (М > 1), то величина ( 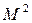 – 1) > 0 и по (8.5) видно, что в этом случае должно быть dF > 0. Следовательно, для разгона сверхзвукового потока канал должен быть расширяющимся (рис. 8.1,б). Из (8.5) следует также, что невозможно осуществить разгон потока от дозвуковой к сверхзвуковой скорости только в суживающемся или только в расширяющемся соплах. Для этой цели необходимо применять комбинированное сопло (рис. 8.1,в), состоящее из суживающегося и расширяющегося участков. В суживающейся части такого сопла поток разгоняется до скорости, равной скорости звука (М = 1), а в расширяющейся части происходит увеличение скорости сверхзвукового потока. Минимальное сечение сопла, в котором скорость потока равна местной скорости звука, принято называть критическим сечением. Параметры потока в этом сечении равны критическим параметрам. В технической литературе суживающиеся – расширяющиеся сопла называются часто соплами Лаваля.
– 1) > 0 и по (8.5) видно, что в этом случае должно быть dF > 0. Следовательно, для разгона сверхзвукового потока канал должен быть расширяющимся (рис. 8.1,б). Из (8.5) следует также, что невозможно осуществить разгон потока от дозвуковой к сверхзвуковой скорости только в суживающемся или только в расширяющемся соплах. Для этой цели необходимо применять комбинированное сопло (рис. 8.1,в), состоящее из суживающегося и расширяющегося участков. В суживающейся части такого сопла поток разгоняется до скорости, равной скорости звука (М = 1), а в расширяющейся части происходит увеличение скорости сверхзвукового потока. Минимальное сечение сопла, в котором скорость потока равна местной скорости звука, принято называть критическим сечением. Параметры потока в этом сечении равны критическим параметрам. В технической литературе суживающиеся – расширяющиеся сопла называются часто соплами Лаваля.
Объясним выявленные закономерности изменения формы сопел, предназначенных для разгона потоков с различными скоростями, базируясь на формуле (8.4), которая устанавливает связь относительного изменения объёма газа 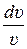 с относительным изменением скорости
с относительным изменением скорости 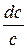 при различных числах Маха.
при различных числах Маха.
Из (8.4) видно, что при дозвуковых скоростях газа (М < 1) относительное изменение объёма меньше относительного изменения скорости 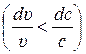 . Следовательно, плотность газа при разгоне дозвукового потока снижается в меньшей степени, чем растет его скорость, что в соответствии с уравнением неразрывности (7.2) требует уменьшения площади проходных сечений вдоль сопла. В потоке, текущем со сверхзвуковой скоростью (М > 1), картина обратная: увеличение скорости сопровождается более интенсивным расширением газа
. Следовательно, плотность газа при разгоне дозвукового потока снижается в меньшей степени, чем растет его скорость, что в соответствии с уравнением неразрывности (7.2) требует уменьшения площади проходных сечений вдоль сопла. В потоке, текущем со сверхзвуковой скоростью (М > 1), картина обратная: увеличение скорости сопровождается более интенсивным расширением газа 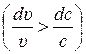 . При таком изменении параметров потока необходимо увеличение площади проходных сечений вдоль сопла.
. При таком изменении параметров потока необходимо увеличение площади проходных сечений вдоль сопла.
Заметим, что при малых дозвуковых скоростях потока (М << 1) без заметного ущерба для точности практических расчётов можно пренебречь изменением объёма газа при изменении его скорости, т. е. рассматривать газ как несжимаемую среду.
Форма диффузора (dc < 0). Проведя с помощью формулы (8.5) анализ, аналогичный проведённому выше для сопла, нетрудно установить, что дозвуковой поток (М < 1) тормозится в расширяющемся канале (dF > 0, рис. 8.2,а). Если на входе в диффузор поток сверхзвуковой (М > 1), то для его торможения необходимо применять суживающийся канал (dF < 0, рис. 8.2,б). Снижение скорости потока от сверхзвуковой к дозвуковой возможно в комбинированном (суживающемся – расширяющемся) диффузоре (рис. 8.2,в), называемом иногда обращённым соплом Лаваля. В суживающейся части такого диффузора скорость сверхзвукового потока снижается до скорости, равной скорости звука (М = 1), а в расширяющейся части проходит торможение дозвукового потока. Минимальное сечение диффузора, где М = 1, принято называть критическим сечением или “горлом”. Причина различного характера изменения площади диффузора для торможения дозвукового и сверхзвукового потоков, как и у сопла, заключается в различной интенсивности уменьшения объёма газа при снижении его скорости (8.4) в случае, когда М > 1 или М < 1.
Следует заметить, что реальный процесс торможения воздуха в диффузорах при сверхзвуковых скоростях потока сопровождается появлением скачков уплотнения, в которых происходит ступенчатое изменение скорости и параметров воздуха при частичной диссипации его энергии. Однако качественно характер изменения параметров потока и площади проходных сечений вдоль диффузора в реальном процессе аналогичен таковым при идеальном торможении. Особенности течения воздуха в сверхзвуковых диффузорах детально изучаются в теории авиационных двигателей.
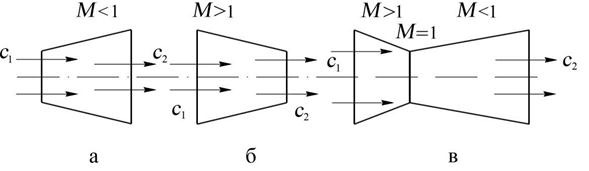
Рис. 8.2. Формы каналов для торможения потоков
8.2. Параметры заторможенного потока
Для решения практических задач с помощью уравнения сохранения энергии должны быть известны параметры состояния движущегося газа.
Замер Т и p в движущемся газе значительно сложнее, чем в неподвижном. Это объясняется тем, что измерительные приборы под воздействием набегающего потока показывают завышенные значения. Чтобы устранить этот недостаток, надо сделать так, чтобы измерительные приборы двигались со скоростью равной скорости потока, в этом случае замеренные параметры называются статическими. Но такой способ замера параметров в проточной части осуществить невозможно.
Используя уравнение сохранения энергии, можно найти другие параметры, которые практически просто позволяют определить параметры движущегося потока. Эти параметры названы полными параметрами или параметрами заторможенного потока и обозначаются такими буквами, как и статические, но со звездочкой: p*, Т*, ρ*, i*. При полном адиабатном торможении газового потока (до нулевой скорости) его кинетическая энергия полностью преображается в тепловую энергию хаотического движения молекул.
Таким образом, параметры заторможенного потока – это параметры газа при его полном адиабатном торможении до нулевой скорости.
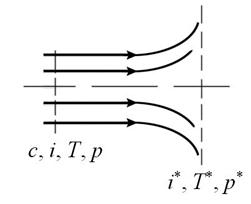 Пусть в некотором сечении газового потока (рис. 8.3.) скорость, энтальпия, температура и давление равны: с, i, Т, p.
Пусть в некотором сечении газового потока (рис. 8.3.) скорость, энтальпия, температура и давление равны: с, i, Т, p.
Рис. 8.3. К выводу формул параметров заторможенного потока
Затормозим условно поток с этими параметрами, считая, что теплообмен с окружающей средой отсутствует, т.е. торможение происходит адиабатно. Параметры адиабатно заторможенного потока обозначим так: i*, Т*, p*. Величины i*, Т* и p* называются соответственно: полная энтальпия, полная температура, полное давление.
Поскольку в рассматриваемом случае Qвнеш = 0, Lвнеш = 0, то считая с* = 0, найдем из (7.10) или (7.17) полную энтальпию:
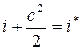 . (8.6)
. (8.6)
Уравнение (8.6) перепишем в виде
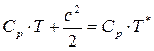 . (8.6')
. (8.6')
Теперь из уравнения (8.6') определим полную температуру
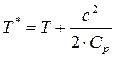 . (8.7)
. (8.7)
Давление заторможенного потока найдется из уравнения адиабатного процесса (3.39)
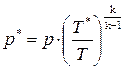 (8.8)
(8.8)
или с учётом (8.7)
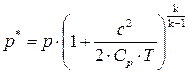 . (8.9)
. (8.9)
Выразим величины Т*, p*, ρ* через число Маха 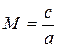 , где а скорость звука.
, где а скорость звука.
Учитывая, что 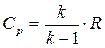 , из (8.7) найдем
, из (8.7) найдем
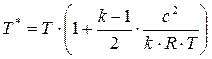 .
.
Поскольку в идеальном газе
k·R·T = a2,
то полная температура через число Маха определяется по формуле:
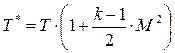 . (8.10)
. (8.10)
Из данного уравнения видно, что полная температура Т* будет существенно отличаться от статической температуры Т при М > 1.
Давление и плотность заторможенного потока можно легко найти, используя формулы соотношения параметров в адиабатном процессе (3.39), (3.41).
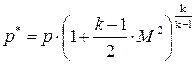 (8.11)
(8.11)
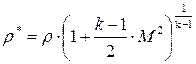 (8.12)
(8.12)
Пример: так для воздуха k = 1,4; при Т = 300 К и М = 5, Т* = 1800 К. При столь высоких температурах ухудшаются прочностные свойства материалов, из которых выполнены конструкции современных ЛА и АД.
8.3. Уравнение сохранения энергии в параметрах
заторможенного потока
Теперь используя выражения энтальпии, температуры и давления в параметрах заторможенного потока можно получить более простые выражения уравнения сохранения энергии для потока.
Учтя (7.16) и (8.6), получим уравнение сохранения энергии в параметрах заторможенного потока.
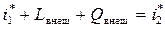 (8.13)
(8.13)
В случае идеального газа этому уравнению можно придать вид:
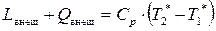 (8.14)
(8.14)
или в дифференциальной форме
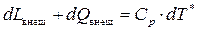 . (8.15)
. (8.15)
Для энергоизолированного потока из (8.13) получаем, что
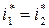 . (8.16)
. (8.16)
Таким образом, в энергоизолированном потоке полная энтальпия газа (сумма энтальпии и кинетической энергии) постоянна.
В случае идеального газа из (8.14) следует
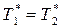 .
.
Следовательно, в энергоизолированном потоке идеального газа полная температура неизменна.
8.4. Измерение параметров потока
С введением полных параметров упрощается замер температуры и давления с помощью специальных датчиков в любом интересующем сечении потока, схемы которых представлены на рис. 8.4.
p* = p + (ρc2)/2 – измеряется с помощью Г – образного насадка, установленного навстречу потоку (рис. 8.4,а).
p можно измерить с помощью простого дренажа стенки (рис. 8.4,б).
Т* замеряется при помощи чувствительного элемента датчика (рис. 8.4,в) температуры, помещаемого в поток.
Т измерить практически невозможно, т. к. необходимо обеспечить движение чувствительного элемента по каналу со скоростью потока, что технически реализовать нереально.
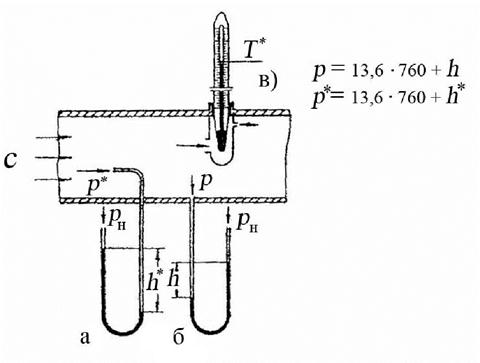
Рис. 8.4. Схемы датчиков для измерения давления (а), температуры (в) заторможенного потока и статического (б) давления
8.5. Изменение полной температуры и полного давления
в газовом потоке
Об изменении Т* в потоке идеального газа можно судить по уравнению сохранения энергии (8.13), которое представим в дифференциальном виде
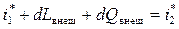 . (8.17)
. (8.17)
Далее преобразуя уравнение (8.17), получим
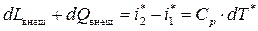 . (8.18)
. (8.18)
Из уравнения (8.18) выразим dT*
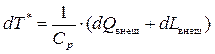 . (8.19)
. (8.19)
Таким образом, полная температура потока может меняться лишь при подводе или отводе внешней энергии в виде тепла или работы. Поэтому полная температура косвенно характеризует запас полной энергии газового потока. В случае энергоизолированного потока, как было показано ранее, dT* = 0.
Интересно отметить, что наличие трения газа не влияет на величину полной температуры. Это связано с тем, что тепло трения компенсируется работой против сил трения.
Рассмотрим изменение полного давления. Логарифмируя и затем, дифференцируя (3.39 или 8.8), получим
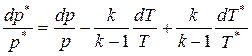 . (8.20)
. (8.20)
Согласно (7.11) и (7.12)
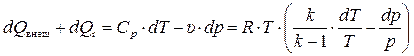 ,
,
откуда
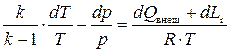 . (8.21)
. (8.21)
Подставляя (8.19) и (8.21) в (8.20), получим
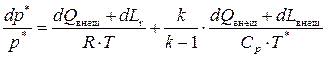 ,
,
или
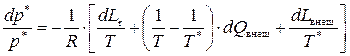 . (8.22)
. (8.22)
Из этого результата следует:
– в энергоизолированном потоке (Qвнеш = 0, Lвнеш = 0) при отсутствии трения (Lr = 0) полное давление не меняется (dp* = 0);
– полное давление потока уменьшается при наличии терния, при подводе внешнего тепла и совершении газом внешней работы (например, в турбине). Уменьшение полного давления газового потока без совершения внешней работы означает уменьшение его работоспособности при данном запасе энергии. Действительно, чем меньше полное давление газа, тем меньше сила, действующая со стороны газового потока на тело, и поэтому меньше работа, которую может совершить газ при данном запасе полной энергии (т. е. при данной величине Т*).
Поэтому можно считать, что трение и подвод тепла к газовому потоку приводят к диссипации (рассеянию) энергии.
Отметим, что степень уменьшения полного давления при подводе тепла тем больше, чем выше число Маха. Действительно, чем больше число М, тем больше разность 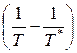 и поэтому выше величина
и поэтому выше величина 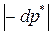 , как это видно из (8.22).
, как это видно из (8.22).
Уменьшение полного давления при подводе тепла к газовому потоку называют тепловым сопротивлением;
– уменьшение p* при подводе Lвнеш (например, в турбине) не означает наличия диссипации энергии, так как это уменьшение сопровождается совершением полезной работы.
8.6. Скорость истечения газа из сопла
Рассмотрим подробно течение газа в соплах. Как и ранее, считаем газ идеальным, а течение происходящим без трения (Lr = 0) и энергообмена (Qвнеш = 0, Lвнеш = 0).
На рис. 8.5. изображено дозвуковое сопло. В сечении 0 – 0 параметры потока определены значениями  и с* = 0.
и с* = 0.
Разгон газа, как отмечалось ранее, сопровождается понижением давления в направлении движения. Определим скорость газа сх в произвольном сечении сопла Х – Х.
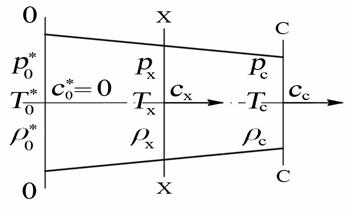
Рис. 8.5. К выводу формулы скорости истечения газа из сопла
Для этого воспользуемся уравнением сохранения энергии записанного для сечений 0 – 0 и Х – Х:
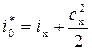 , (8.23)
, (8.23)
откуда определяем
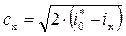 . (8.24)
. (8.24)
Так как газ идеальный, то
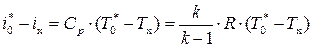 .
.
Тогда
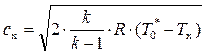 . (8.25)
. (8.25)
Поскольку рассматривается адиабатный процесс расширения газа в сопле, то
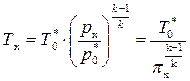 ,
,
где  – степень понижения давления газа в сечении сопла X– X.Поэтому скорость газа сx в произвольном сечении сопла определяется следующими формулами
– степень понижения давления газа в сечении сопла X– X.Поэтому скорость газа сx в произвольном сечении сопла определяется следующими формулами
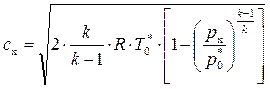 (8.26)
(8.26)
или
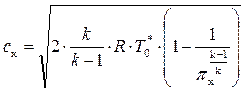 . (8.27)
. (8.27)
По аналогии с (8.27) напишем формулу для скорости истечения газа из сопла
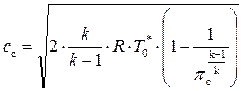 , (8.28)
, (8.28)
где 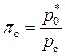 – действительная степень понижения давления газа в сопле.
– действительная степень понижения давления газа в сопле.
Значения сх, сс – это значения теоретической скорости, сх – скорость течения газа в произвольном сечении сопла X – X и сс – скорость истечения газа в выходном сечении сопла С – С. А действительная скорость всегда меньше теоретической вследствие потерь на трение. Эти потери учитываются поправочным коэффициентом скорости φс (φс = сс / сс ад). Обычно значение этого коэффициента лежит в пределах 0,985…0,92.
Уравнение (8.28) показывает, что скорость истечения газа из сопла зависит от свойств газа (k, R), его полной температуры ( 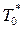 ) перед соплом и действительной степени понижения давления газа в сопле (πс).
) перед соплом и действительной степени понижения давления газа в сопле (πс).
сс = f (k, R, 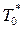 ,
, 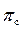 )
)
Исследуем характер изменения скорости истечения газа из сопла сс в зависимости от πс при условии, что pc = pH, т. е. происходит полное расширение газа в сопле до давления окружающей среды pH. При постоянных параметрах на входе в сопло изменить πс можно путем изменения давления pH от 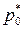 до нуля.
до нуля.
Зависимость скорости истечения сс от πс показана на рис. 8.6. Из этого рисунка и формулы (8.28) видно, что при πс = 1 скорость сс = 0, а при πс = πкр, скорость сс = скр (Мс = 1). Если величина πс стремится к бесконечности, то скорость истечения стремится к предельной величине сс = сс max, которая достигается при истечении в вакуум (pH = 0) и определяется по формуле:
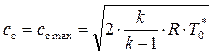 , (8.29)
, (8.29)
т. е. максимальная скорость истечения газа из сопла определяется полной температурой 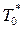 на входе в сопло и родом рабочего тела (k, R).
на входе в сопло и родом рабочего тела (k, R).
Как видно из (8.29), максимально возможная скорость истечения газа даже при πс = ∞ имеет конечное значение. Это объясняется тем, что при энергоизолированном течении увеличение скорости и соответственно кинетической энергии газа происходит за счёт уменьшения его энтальпии, которая не может быть бесконечной.
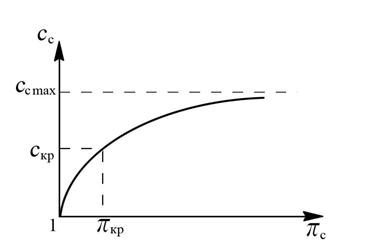
Рис. 8.6. График зависимости сс = f (πс), при 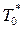 = const
= const
Однако практически такая скорость не может быть достигнута, так как при падении температуры, сопровождающей рост скорости, газ теряет свойства идеального ещё задолго до достижения максимальной скорости.
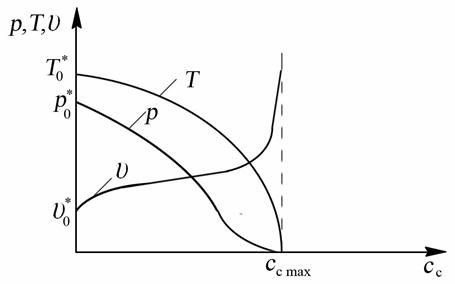
Рис. 8.7. Зависимости параметров состояния газа от скорости его движения
Выясним теперь зависимость параметров состояния рабочего тела от скорости его движения. Как было показано (вопрос 8.1.), при увеличении скорости потока давление уменьшается. Так как процесс течения адиабатный, температура изменяется пропорционально, а удельный объём обратно пропорционально давлению. Зависимости параметров состояния от скорости движения рабочего тела представлены на рис. 8.7. Итак, рост скорости сопровождается падением давления и температуры и возрастанием удельного объёма. Рост удельного объёма показывает, что совершается работа расширения, которая затрачивается на увеличение кинетической энергии потока.
Как указывалось, в суживающемся сопле возможно разогнать поток только до скорости, равной местной скорости звука. Поэтому максимальная скорость истечения газа из суживающегося сопла ограничена значением критической скорости скр.
8.7. Критические параметры газового потока.
Критическая скорость
В предыдущем вопросе было показано, что рост скорости рабочего тела (газа) при адиабатном движении по соплу сопровождается падением его температуры. Это приводит к уменьшению скорости звука в соответствии с уравнением
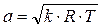 .
.
Очевидно, что в некотором сечении сопла скорость потока и местная скорость звука (скорость звука в данном сечении) равны. Это сечение называется критическим. Все параметры потока в этом сечении также называются критическими и обозначаются pкр, Ткр, ρкр, скр и т.д. (рис. 8.8.).
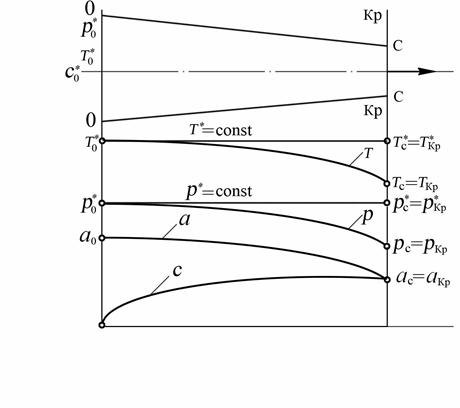
Рис. 8.8. Изменение параметров газа, его скорости и скорости звука
по длине сопла
Для критического сечения справедливо следующее соотношение:
 . (8.30)
. (8.30)
Критические параметры легко определяются, если известны параметры на входе в сопло. Используя зависимости между статическими и заторможенными (полными) параметрами, найдем связь между критическими и полными параметрами потока.
Из уравнения (8.10) имеем:
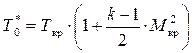 , т. к. Мкр = 1 получаем
, т. к. Мкр = 1 получаем
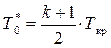 . (8.31)
. (8.31)
Из (8.31) определяем Ткр
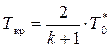 . (8.32)
. (8.32)
Для воздуха k = 1,4, следовательно, Ткр = 0,833 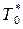 . Это означает, что критическая скорость достигается в том сечении сопла, в котором температура составит 83,3 % полной температуры
. Это означает, что критическая скорость достигается в том сечении сопла, в котором температура составит 83,3 % полной температуры 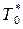 на входе в сопло. Однако следует помнить, что полная температура в любом сечении сопла, в том числе и критическом, равна полной температуре на входе в сопло:
на входе в сопло. Однако следует помнить, что полная температура в любом сечении сопла, в том числе и критическом, равна полной температуре на входе в сопло: 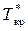 =
= 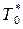 . Критическое давление легко определяется из соотношения параметров в адиабатном процессе (3.39) и используя найденное уравнение Ткр (8.32)
. Критическое давление легко определяется из соотношения параметров в адиабатном процессе (3.39) и используя найденное уравнение Ткр (8.32)
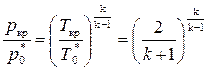
или
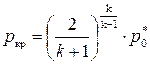 . (8.33)
. (8.33)
Для воздуха k = 1,4, поэтому pкр = 0,528 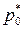 , т. е. критическое давление составляет 52,8 % полного давления на входе в сопло.
, т. е. критическое давление составляет 52,8 % полного давления на входе в сопло.
Аналогично определяется плотность газа в критическом сечении:
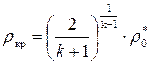 . (8.34)
. (8.34)
Для воздуха k = 1,4, поэтому ρкр = 0,634 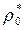 , таким образом, плотность газа в критическом сечении уменьшается на 36,6 % по сравнению с плотностью заторможенного потока на входе в сопло.
, таким образом, плотность газа в критическом сечении уменьшается на 36,6 % по сравнению с плотностью заторможенного потока на входе в сопло.
По определению (8.30) критическая скорость равна:
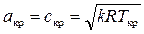 .
.
или с учётом (8.32)
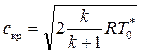 . (8.35)
. (8.35)
Таким образом, критические параметры потока и критическая скорость для данного газа полностью определяются соответствующими полными заторможенными параметрами.
Отношение полного давления на входе в сопло к статическому давлению его в критическом сечении называется критической степенью понижения давления πкр, т. е.
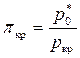 . (8.36)
. (8.36)
С учётом (8.33) имеем
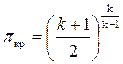 . (8.37)
. (8.37)
Для воздуха k = 1,4; следовательно, πкр = 1,89, для газа k = 1,33; поэтому πкр = 1,85. Если степень понижения давления воздуха (газа) π < πкр, она называется докритической, при π > πкр – сверхкритической. Значение π важно знать, так как степень понижения давления определяет возможность получения дозвуковой или сверхзвуковой скорости его движения.
8.8. Основные газодинамические функции и их использование
при расчётах газовых потоков
Мы выяснили, что скорость истечения газов зависит не только от πс (pс, 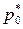 ) и
) и 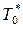 , но и от формы сопла. Форма сопла должна быть не цилиндрической трубой, а специально спрофилированной. В таком сопле при изменении скорости происходит одновременное изменение параметров состояния газа.
, но и от формы сопла. Форма сопла должна быть не цилиндрической трубой, а специально спрофилированной. В таком сопле при изменении скорости происходит одновременное изменение параметров состояния газа.
Для расчёта изменения параметров газа при его движении в каналах, в том числе и соплах, в газовой динамике широко используются газодинамические функции (приведенные параметры или относительные параметры). Газодинамические функции представляют собой отношения действительных (статических) параметров в любом сечении потока к значению тех же параметров заторможенного потока, в каком либо другом, сравнительном сечении.
Таким образом, значение параметра в сравнительном сечении является как бы мерой, масштабом для значения данного параметра во всех других сечениях.
В расчётной практике сложилась традиция брать в качестве масштабов для одних величин значения параметров торможения, для других – значения критических параметров.
Главную роль при расчётах играют следующие газодинамические функции:
– температуры 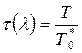 ; (8.38)
; (8.38)
– давления 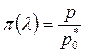 ; (8.39)
; (8.39)
– плотности 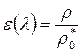 ; (8.40)
; (8.40)
– плотности тока газа 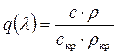 ; (8.41)
; (8.41)
Газодинамическая функция q (λ) имеет важное значение в термодинамике газового потока, так как она характеризует расход газа.
– сжимаемости 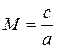 . (8.42)
. (8.42)
Число Маха представляет собой безразмерную (относительную) скорость потока, причём масштабом скорости здесь является местная скорость звука а.
Все газодинамические функции являются безразмерными параметрами потока. Газодинамические функции позволяют значительно облегчить проведение расчётов авиационных ГТД. Значение этих функций обычно представляются в виде таблиц (смотри приложение П.4), где аргументом выступает коэффициент скорости λ или её называют приведённой скоростью.
Коэффициент скорости λ – отношение действительной скорости потока в любом рассматриваемом сечении потока (сх) к значению критической скорости (скр).
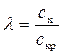 (8.43)
(8.43)
или
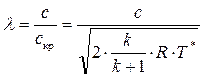 , (8.43')
, (8.43')
где Т* вычисляется в точке потока к которой относится скорость с.
В формулах (8.43), (8.43') масштабом скорости принимается критическая скорость.
Коэффициент скорости λ имеет вполне конкретные значения. Найдём их. Скорость газа с при его движении по соплу может теоретически изменяться от нуля до скр, а потом достигнуть сmax. Критическая скорость скр для данного газа при 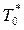 = const является величиной постоянной, следовательно коэффициент скорости λ может принимать значения от λ = 0 до λ = λmax, так как при значении
= const является величиной постоянной, следовательно коэффициент скорости λ может принимать значения от λ = 0 до λ = λmax, так как при значении
сх = 0, λ = 0;
сх = скр, λ = 1;
сх = сmax, λ = λmax.
Определим значения λmax для воздуха, для которого k = 1,4; R = 287 Дж / (кг ∙ К).
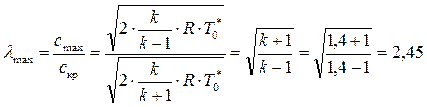 . (8.44)
. (8.44)
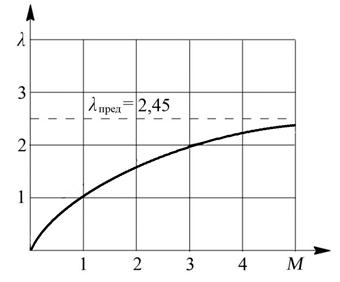 Зависимости скорости потока от коэффициента скорости и зависимости λ = f (M) показаны соответственно на рис. 8. 9. и рис. 8.10.
Зависимости скорости потока от коэффициента скорости и зависимости λ = f (M) показаны соответственно на рис. 8. 9. и рис. 8.10.
Рис. 8.9. График зависимости λ = f (M) для k = 1,4; R = 287 Дж / (кг ∙ К)
Таким образом, коэффициент скорости λ для воздуха может иметь конкретные числовые значения
0 < λ < 2,45.
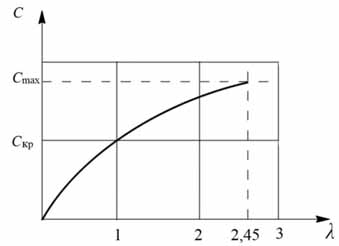
Рис. 8.10. График зависимости с = f (λ) для k = 1,4; R = 287 Дж / (кг ∙ К)
Поэтому газодинамические функции выражают через коэффициент скорости. Получим формулы для вычисления газодинамических функций
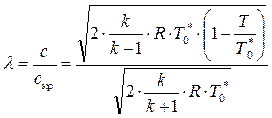 . (8.45)
. (8.45)
После преобразования (8.45) получим газодинамическую функцию температуры, где аргументом выступает коэффициент скорости λ, т. е.
 . (8.46)
. (8.46)
Далее используя адиабатные зависимости между параметрами состояния газа, можно получить газодинамические функции давления и плотности
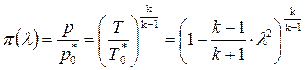 , (8.47)
, (8.47)
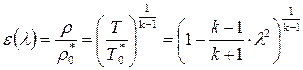 . (8.48)
. (8.48)
Используя известные формулы, можно выразить через коэффициент скорости и другие газодинамические функции.
Преобразуем (8.41) и получим газодинамическую функцию плотности тока газа
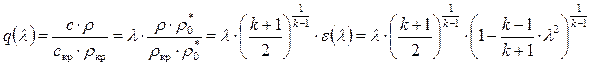 .(8.49)
.(8.49)
Величина q (λ) связана с расходом газа следующим образом:
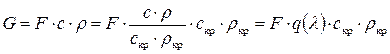 . (8.50)
. (8.50)
Газодинамическая функция сжимаемости М однозначно связана с коэффициентом скорости λ. Действительно
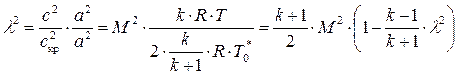 (8.51)
(8.51)
или
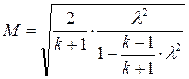 . (8.52)
. (8.52)
Построим график изменения функций τ, π, ε, q в зависимости от λ для воздуха (k =1,4; λmax = 2,45), используя уравнения (8.46; 8.47; 8.48; 8.49) и подставив в них значения λ = 0; λ = 1; λ = λmax. В результате получим:
при λ = 0 → τ (λ) = π (λ) = ε (λ) = 1; q (λ) = 0
при λ = 1 → τ (λ) = 0,833; π (λ) = 0,528; ε (λ) = 0,634; q (λ) = 1
при λ = λmax = 2,45 → τ (λ) = π (λ) = ε (λ) = q (λ) = 0.
Полученные результаты используем для построения графиков газодинамических функций, которые приведены на рис. 8.11.
Этими графиками можно пользоваться только для решения задач, не требующих высокой точности расчёта. Для более точных расчётов следует использовать таблицы газодинамических функций, в которых приводятся значения функций от λ с точностью до 5 – 7-го знака (Приложение П.4).
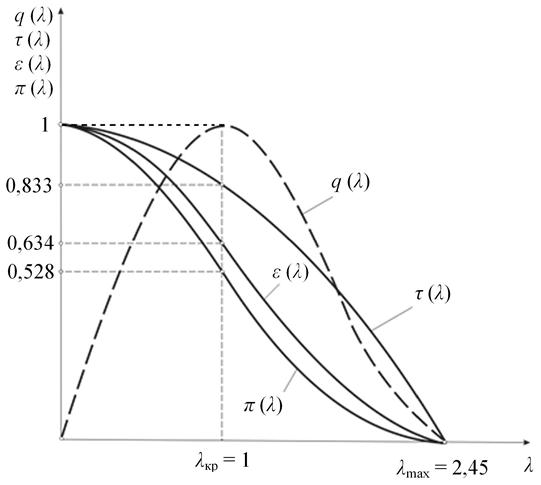
Рис. 8.11. Графическое изображение газодинамических функций
Таблицы газодинамических функций, заранее рассчитанные и приведённые в виде таблиц, существенно упрощают анализ и расчёт газовых потоков.
Здесь рассмотрены пять наиболее употребительных газодинамических функций. В расчётах иногда используют и другие величины, описание и таблицы которых приведены в приложении П.4.
8.9. Идеальное течение газа в соплах. Основные положения
Рассмотрим более подробно течение газа в соплах. Как и ранее, считаем газ идеальным, а течение – происходящим без трения и энергообмена с окружающей средой. Разгон газа, как отмечалось, сопровождается понижением давления. Поэтому давление газа перед соплом всегда должно быть выше, чем давление окружающей среды, в которую происходит истечение газа. На рис. 8.5. и 8.8. и 8.1,в приведены схемы рассматриваемых далее суживающегося сопла и сопла Лаваля и даны обозначения их характерных сечений.
Основные определения. Располагаемой степенью понижения давления газа в сопле называется отношение полного давления газа на входе в сопло к давлению окружающей среды,
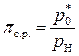 . (8.53)
. (8.53)
Действительной степенью понижения давления газа в сопле называется отношение полного давления газа на входе в сопло к давлению в выходном сечении сопла,
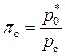 . (8.54)
. (8.54)
Степень понижения давления газа, при которой газ разгоняется до скорости, равной местной скорости звука, называется критической, критическая степень понижения давления газа определена формулами (8.36) и (8.37)
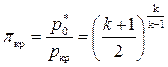 . (8.55)
. (8.55)
Как видно из (8.55), критическая степень понижения давления зависит только от показателя адиабаты k (табл. 8.1).
Таблица 8.1
Величина πкр при разных значениях k
| k | 1,15 | 1,25 | 1,33 | 1,40 | 1,67 |
| πкр | 1,741 | 1,802 | 1,851 | 1,893 | 2,055 |
Различают следующие режимы работы сопла:
1. Режим полного расширения, когда давление в выходном сечении сопла равно давлению окружающей среды, pс = pН. В этом случае, как нетрудно увидеть, πс = πср. Для сопла Лаваля такой режим работы принято называть также расчётным.
2. Режим недорасширения (неполного расширения), когда давление в выходном сечении сопла выше давления окружающей среды, pс > pН. В этом случае πс < πср и окончательное расширение газа и понижение его давления до величины pН происходит за пределами сопла.
3. Режим перерасширения, когда давление в выходном сечении сопла ниже давления окружающей среды, pс < pН. Соответственно, πс > πср. Режим перерасширения, как будет показано ниже, реализуется только в сопле Лаваля.
Рассмотрим особенности изменения параметров потока газа в соплах при различных режимах его работы.
8.10. Режимы работы дозвукового сопла
Дозвуковое сопло может работать на расчётных и нерасчётных режимах.
8.10.1. Изменение параметров потока в суживающемся (дозвуковом) сопле.
Рассмотрим особенности идеального течения газа в суживающемся сопле. Поскольку рассматриваемое течение является энергоизолированным и происходящим без трения, то параметры заторможенного потока газа (Т*, p*, ρ*) по длине сопла остаются неизменными. Падение статического давления вдоль сопла (– dp) приводит, как отмечалось, к росту скорости газа. Увеличение кинетической энергии потока, в свою очередь, понижает энтальпию и температуру газа. В общем случае скорость истечения из суживающегося сопла определяется по формуле (8.28)
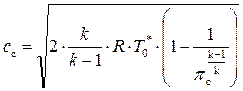 ,
,
а температура газа в выходном сечении сопла Тс по формуле:
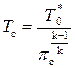 . (8.56)
. (8.56)
Вследствие снижения температуры газа величина местной скорости звука вдоль сопла уменьшается.
Характер истечения газа из суживающегося сопла полностью определяется соотношением между величинами располагаемой и критической степеней понижения давления (πс.р. и πкр). Исследуем особенности течения газа при разных соотношениях между πс.р. и πкр. Для газа с неизменными физическими свойствами величина πкр постоянна (см. табл. 8.1). Поэтому соотношение между πс.р. и πкр может изменяться лишь за счёт увеличения или уменьшения πс.р.. Отметим, что величина πс.р. может изменяться как с изменением давления перед соплом 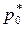 , так и с изменением давления окружающей среды pН.
, так и с изменением давления окружающей среды pН.
8.10.2. Работа дозвукового сопла на расчётном режиме
Рассмотрим расчётный режим работы сопла, при котором давление на выходе из сопла pс равно давлению окружающей среды pН. На расчётном режиме очевидно, что
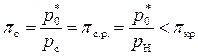 . (8.57)
. (8.57)
При данном условии в сопле происходит полное расширение газа, давление в выходном сечении сопла равно давлению окружающей среды (pс = pН) и поэтому действительная степень понижения давления газа в сопле равна располагаемой (πс = πс.р.). Поскольку πс.р. < πкр, то располагаемой степени понижения давления не хватает для разгона газа для скорости звука. Скорость истечения газа из сопла в этом случае меньше скорости звука (сс < ас и Мс < 1). Характер изменения параметров потока вдоль сопла при данном соотношении между πс.р. и πкр показан на рис. 8.12,а.
При дозвуковых скоростях истечениях газа режим работы сопла всегда расчётный. Это объясняется тем, что любое изменение pН в виде волн слабых возмущений проникает внутрь сопла, вызывая изменения давления в сопле при одновременном изменении скорости.
Например: увеличение высоты полета (Н) вызывает уменьшение давления pН, тогда слабые возмущения вызванные уменьшением pН, распространяясь навстречу дозвуковому потоку (сс < ас) внутрь сопла «предупреждают» его об уменьшении pН. В результате происходит перестройка потока на новые условия до тех пор, пока давление pс не станет равным новому значению pН. И одновременно из – за роста 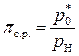 , произойдет увеличение скорости потока, а режим работы сопла остается расчётным.
, произойдет увеличение скорости потока, а режим работы сопла остается расчётным.
Если располагаемая степень понижения давления газа в сопле равна критической (πс = πкр), то в этом случае скорость истечения газа из сопла равна местной скорости звука (сс = ас, Мс = 1). Расширение газа в сопле полное (pс = pН), и действительная степень понижения давления газа равна располагаемой (πс = πс.р. = πкр). Такой режим работы сопла можно рассматривать как предельный из режимов с полным расширением газа в сопле, когда при полном использовании располагаемой степени понижения давления в суживающемся сопле достигается максимально возможная скорость потока.
Изменение параметров потока вдоль сопла при πс.р. = πкр показано на рис. 8.12,б. В выходном сечении сопла скорость и параметры потока равны критическим, которые определяются по уравнениям (8.32) … (8.35).
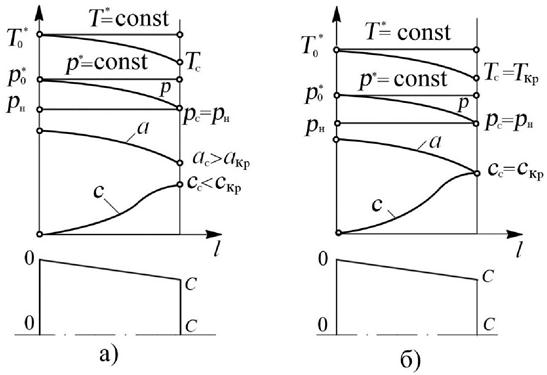
Рис. 8.12. Характер изменения параметров потока вдоль сопла:
а – при πс.р. < πкр и б – при πс.р. = πкр
8.10.3. Работа дозвукового сопла на нерасчётном режиме
Нерасчётным режимом работы сопла называется такой режим, при котором давление газа на выходе из сопла больше давления окружающей среды, т. е. pс > pН.
Следовательно, условием нерасчётного режима является, что располагаемая степень понижения давления газа в сопле больше критической (πс.р. > πкр). Несмотря на повышение величины πс.р. в области πс.р. > πкр, скорость истечения газа из сопла остается равной критической (сс = ас = акр; Мс = 1), так как в суживающемся сопле нельзя разогнать поток до скорости, превышающей местную скорость звука. Соответственно температура, плотность, давление и скорость газа в выходном сечении сопла, а также величина πс остаются равными критическим значениям:
pс = pкр, Тс = Ткр, ρс = ρкр, сс = скр, πс.р. = πкр.
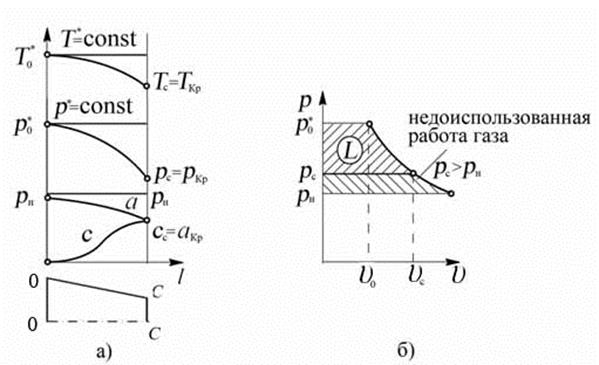 Основной особенностью данного режима работы суживающегося сопла является то, что расширение газа в сопле неполное – давление газа в выходном сечении сопла выше давления окружающей среды (pс > pН), а действительная степень понижения давления меньше располагаемой (πс < πc.р.). Следовательно, располагаемая степень понижения давления газа полностью не используется в сопле для увеличения скорости потока, газ покидает сопло, унося с собой неиспользованную энергию (рис. 8.13,б.).
Основной особенностью данного режима работы суживающегося сопла является то, что расширение газа в сопле неполное – давление газа в выходном сечении сопла выше давления окружающей среды (pс > pН), а действительная степень понижения давления меньше располагаемой (πс < πc.р.). Следовательно, располагаемая степень понижения давления газа полностью не используется в сопле для увеличения скорости потока, газ покидает сопло, унося с собой неиспользованную энергию (рис. 8.13,б.).
Рис. 8.13. Характер изменения параметров потока вдоль сопла при πс.р. > πкр
В области значений πс.р. > πкр изменение внешних условий не сказывается на характере течения газа в сопле. В частности изменение давления pН и связанное с ним изменение πс.р. не влияют на параметры потока в выходном сечении сопла. Физически это объясняется тем, что возмущения в виде изменения давления распространяются в газе со скоростью звука. В случаях, когда в выходном сечении сопла скорость истечения газа равна местной скорости звука, изменение давления окружающей среды не может распространяться навстречу потоку внутрь сопла и повлиять на течение газа в нем. Сопло при этом как бы заперто.
Заметим, что хотя в области πс.р. > πкр скорость истечения газа из суживающегося сопла сс не может быть больше местной скорости звука, повысить её можно за счёт увеличения температуры газа на входе в сопло 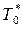 , так как величина скорости звука с ростом температуры газа растёт.
, так как величина скорости звука с ростом температуры газа растёт.
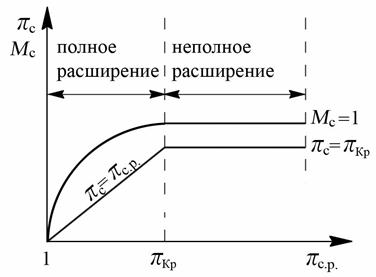
Рис. 8.14. Зависимости πс = f (πс.р.), Мс = f (πс.р.)
На рис. 8.14. показаны зависимости πс и числа Мс (или что тоже – скорости истечения сс) от πс.р.. В области 1 < πс.р. < πкр сопло работает с полным расширением газа (πс = πс.р.), поэтому зависимость πс от πс.р. здесь представляет собой прямую линию, выходящую из начала координат под углом 45°. Число Мс и соответственно скорость истечения сс с ростом πс.р. увеличиваются, достигая при πс.р. = πкр критических величин (Мс = 1; сс = скр,). Дальнейшее увеличение πс.р. в области πс.р. > πкр не изменяет, как указывалось ранее, ни πс, Мс.
На основе сказанного, рис. 8.14. можно выделить две характерные области: область полного расширения газа в сопле (1 < πс.р. < πкр) и область недорасширения (при πс.р. > πкр).
В результате недорасширения газ покидает сопло, унося с собой неиспользованную энергию. Таким образом, в режиме недорасширения не вся энергия газа используется для увеличения скорости, часть её теряется (рис. 8.13,б.).
8.11. Режимы работы сверхзвукового сопла (сопла Лаваля)
Сопла Лаваля применяются в тех случаях, когда необходимо получение сверхзвуковых скоростей истечения. Сверхзвуковое сопло может работать на расчётном и нерасчётном режимах. В отличие от дозвукового сопла в сверхзвуковом сопле при определённом условии могут возникнуть два нерасчётных режима:
а) режим недорасширения (pс > pН);
б) режим перерасширения (pс < pН).
Сверхзвуковые скорости истечения могут быть достигнуты, если располагаемая степень понижения давления превосходит критическую величину. Поэтому далее мы будем рассматривать процесс истечения из сопла Лаваля при условии, что πс.р. > πкр.
8.11.1. Изменение параметров потока вдоль сопла Лаваля
При идеальном энергоизолированном течении газа параметры потока изменяются вдоль сопла Лаваля так, как показано на рис. 8.15. В суживающейся части сопла поток разгоняется до скорости звука, которая достигается в критическом (минимальном) сечении сопла. Течение газа и изменение параметров потока до критического сечения сопла полностью аналогично течению в суживающемся сопле при πс.р. ≥ πкр (см. рис. 8.13.). В расширяющейся части сопла происходит разгон сверхзвукового потока. Скорость газа вдоль сопла монотонно растёт, а давление и температура падают. При этом в сопле Лаваля, как и в суживающемся сопле, при отсутствии трения и теплообмена со стенками температура и давление заторможенного потока будут постоянными (Т* = const, p* = const) вдоль сопла.
Важной характеристикой сопла Лаваля является относительная площадь выходного сечения (геометрическая степень расширения) сопла
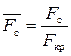 .
.
Из уравнения неразрывности, записанного для критического и выходного сечений, следует:
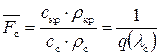 . (8.58)
. (8.58)
Аналогично для произвольного сечения сопла с площадью F можно записать
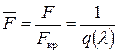 . (8.59)
. (8.59)
При заданной величине показателя адиабаты k существует однозначная связь (см. вопрос 8.8) между относительной плотностью тока q (λ) и остальными газодинамическими функциями М, λ, τ(λ), π(λ), ε(λ), определяющими при заданных значениях 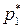 и
и 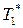 параметры потока в рассматриваемом произвольном сечении сопла. Таким образом, если известен закон профилирования сопла Лаваля, т. е. изменение площади проходных сечений по длине сопла, то это позволяет определить изменение относительной плотности тока q(λ) и остальных газодинамических функций, а соответственно и всех параметров потока, вдоль сопла.
параметры потока в рассматриваемом произвольном сечении сопла. Таким образом, если известен закон профилирования сопла Лаваля, т. е. изменение площади проходных сечений по длине сопла, то это позволяет определить изменение относительной плотности тока q(λ) и остальных газодинамических функций, а соответственно и всех параметров потока, вдоль сопла.
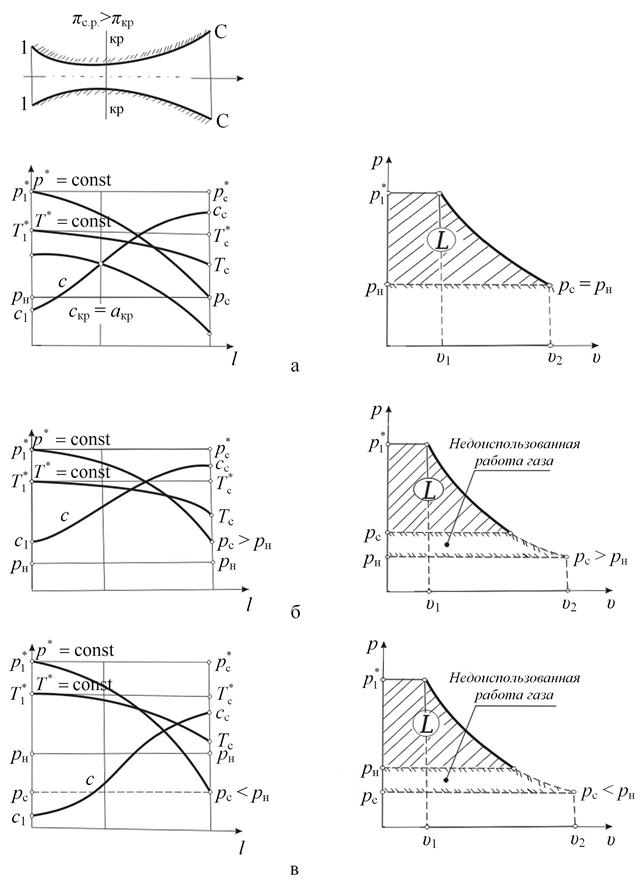
Рис. 8.15. Режимы течения в сверхзвуковом сопле: а – расчётный режим, б – режим с недорасширением, в – режим с перерасширением
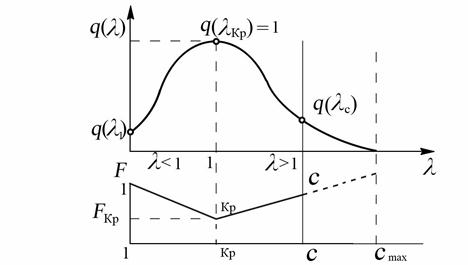
Рис. 8.16. Характер изменения q(λ) в сопле Лаваля
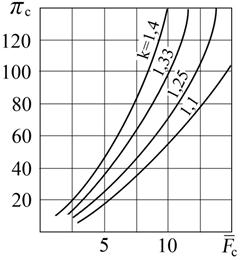
Рис. 8.17. Зависимость 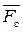 = f (πc)
= f (πc)
8.11.2. Влияние 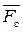 на течение газа в сопле
на течение газа в сопле
На рис. 8.16. показано изменение относительной плотности тока q(λ) в сопле Лаваля. В критическом сечении относительная плотность тока достигает максимального значения q(λкр) = 1, а суживающейся и расширяющейся частях сопла q(λ) снижается при увеличении F.
Действительная степень понижения давления газа в сопле πc связана с величиной 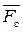 . Установим эту связь, используя равенство расходов газа в критическом и выходном сечениях сопла
. Установим эту связь, используя равенство расходов газа в критическом и выходном сечениях сопла
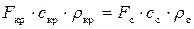 .
.
Подставив в это равенство значения величин, определяемые формулами (8.34), (8.35), (8.28), (3.34), получим
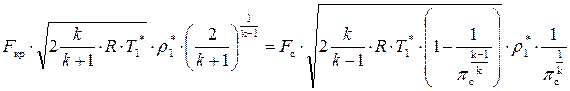 .
.
После сокращений и несложных преобразований приводим уравнение к виду:
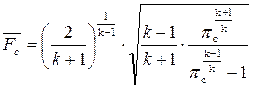 . (8.60)
. (8.60)
На рис. 8.17. зависимость (8.60) представлена графически. Видно, что при заданном показателе k существует однозначная связь между 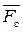 и πc. Чем больше относительная площадь выходного сечения сопла
и πc. Чем больше относительная площадь выходного сечения сопла 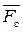 , тем больше πc и тем больше скорость истечения газа из сопла сс и число Мс. В сопле Лаваля с неизменной геометрией (
, тем больше πc и тем больше скорость истечения газа из сопла сс и число Мс. В сопле Лаваля с неизменной геометрией ( 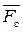 = const) течение газа происходит при постоянном значении πc, величина которой не изменяется при отклонении
= const) течение газа происходит при постоянном значении πc, величина которой не изменяется при отклонении 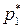 или pH (и соответствующей им величины πc.р.) от расчётных значений, если при этом не происходит отрыва потока от стенок сопла. Следовательно, расчётный режим работы сопла Лаваля (pc = pH) при заданных значениях на входе
или pH (и соответствующей им величины πc.р.) от расчётных значений, если при этом не происходит отрыва потока от стенок сопла. Следовательно, расчётный режим работы сопла Лаваля (pc = pH) при заданных значениях на входе 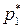 и окружающей среды pH обеспечивается только при единственном значении
и окружающей среды pH обеспечивается только при единственном значении 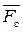 , которое может быть вычислено по (8.60) или определено из рис. 8.17. Если же геометрия сопла задана (известно значение
, которое может быть вычислено по (8.60) или определено из рис. 8.17. Если же геометрия сопла задана (известно значение 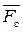 ), то каждому значению давления pH на расчётном режиме соответствует определенная величина давления
), то каждому значению давления pH на расчётном режиме соответствует определенная величина давления 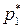 , которая также может быть найдена по (8.60) или из рис. 8.17. по величине πc.
, которая также может быть найдена по (8.60) или из рис. 8.17. по величине πc.
Из сказанного следует также, что отношения одноименных параметров газа перед соплом и в выходном сечении также однозначно определяются величиной 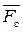 . Действительно, поскольку
. Действительно, поскольку
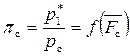 ,
,
то в соответствии с уравнениями связи параметров состояния в адиабатном процессе можно записать
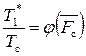 и
и 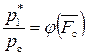 .
.
Если же 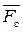 = const, то
= const, то
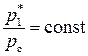 ,
, 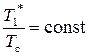 и
и 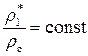 .
.
Следовательно, при 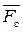 = const изменение давления и температуры газа на входе в сопло (
= const изменение давления и температуры газа на входе в сопло ( 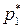 ,
, 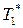 ) вызывает пропорциональное изменение давления и температуры в выходном сечении сопла (pс, Тс). Проводя аналогичные рассуждения для произвольного сечения сопла Лаваля с площадью F, можно установить, что изменение
) вызывает пропорциональное изменение давления и температуры в выходном сечении сопла (pс, Тс). Проводя аналогичные рассуждения для произвольного сечения сопла Лаваля с площадью F, можно установить, что изменение 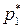 и
и 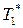 вызывает пропорциональное изменение давления и температуры в рассматриваемом произвольном сечении, а, следовательно, и по всей длине сопла.
вызывает пропорциональное изменение давления и температуры в рассматриваемом произвольном сечении, а, следовательно, и по всей длине сопла.
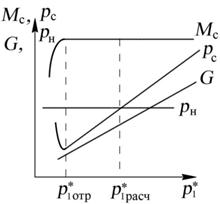
Рис. 8.18. Зависимость pc, Mc, G от p1* при 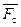 = const и
= const и 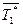 = const
= const
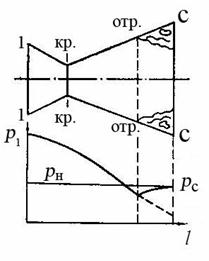
Рис. 8.19. Схема отрывного течения газа в сопле Лаваля
8.11.3. Влияние 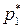 и pH на течение газа в сопле
и pH на течение газа в сопле
На рис. 8.18. показана зависимость давления в выходном сечении pс, числа Мс (что эквивалентно скорости сс) и расхода газа через сопло G от давления на входе в сопло 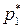 при заданной геометрии сопла (
при заданной геометрии сопла ( 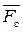 = const) и
= const) и 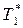 = const. При
= const. При 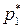 =
= 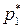 расч сопло работает на расчётном режиме (pс расч = pH, πc = πc.р.). Увеличение
расч сопло работает на расчётном режиме (pс расч = pH, πc = πc.р.). Увеличение 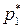 (и соответственно πc.р.) прив
(и соответственно πc.р.) прив
| <== предыдущая страница | | | следующая страница ==> |
| ТЕМА 7. ОСНОВНЫЕ УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ | | | ТАНЦЕВАЛЬНЫЕ ДИСЦИПЛИНЫ СОБЫТИЯ |
Дата добавления: 2014-09-08; просмотров: 4487; Нарушение авторских прав

Мы поможем в написании ваших работ!