
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
КОЛЛИГАТИВНЫЕ СВОЙСТВА РАСТВОРОВ
Ранее уже отмечалось, что растворы, являясь многокомпо-нентными системами, приобретают некоторые свойства, которыми не обладают отдельные компоненты раствора. Для химии большой интерес представила бы возможность определения свойств растворов по известным характеристикам индивидуальных компонентов. Однако в настоящее время такая задача не решена и общая теория растворов не создана.
В то же время термодинамическая теория растворов позволяет устанавливать взаимосвязь между отдельными характеристиками раствора. Иными словами, можно вычислять одни параметры раствора, если известны другие.
Основными независимыми переменными в теории растворов являются концентрация, температура и давление. В некоторых случаях число переменных, необходимых для расчета остальных параметров раствора, удается свести к минимуму. Так, определенные свойства разбавленного раствора нелетучего неэлектролита можно рассчитать, зная только концентрацию раствора и при этом абстрагируясь от химической природы растворенного вещества.
Свойства растворов, которые зависят только от концентрации компонентов, но не зависят от их природы, называются коллигативными.
К коллигативным свойствам растворов относят:
1) понижение давления насыщенного пара над раствором по сравнению с растворителем;
2) повышение температуры кипения и понижение температуры замерзания (кристаллизации) растворов по сравнению с раствори-телем;
3) осмотические явления.
Давление насыщенного пара.
Закон Рауля
Пар, находящийся в динамическом равновесии со своей жидкостью называется насыщенным. Насыщенный пар характери-зуется давлением P (Па, атм), которое иногда называют упругостью пара. Давление насыщенного пара зависит от природы жидкости и от температуры. С ростом температуры давление насыщенного пара возрастает (рис. 1.).

Рис. 1. Зависимость давления насыщенного пара растворителя от температуры.
Добавление в растворитель растворенного вещества (нелетучего неэлектролита) приводит к тому, что на протяжении всего температурного интервала давление насыщенного пара растворителя над раствором (кривая 2) ниже давления насыщенного пара над чистым растворителем (кривая 1). Это связано с уменьшением количества свободных молекул растворителя на поверхности жидкости.
Закон Рауля:
Относительное понижение давления пара растворителя над раствором нелетучего неэлектролита равно мольной доле раство-ренного вещества:
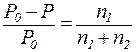 , ,
| (1) |
где Р – давление насыщенного пара растворителя над раствором
(атм; Па; мм. рт. ст.);
Р0 – давление насыщенного пара над чистым растворителем
(атм; Па; мм. рт. ст.);
n1 – количество растворенного вещества (моль);
n2 – количество растворителя (моль).
Температура, при которой давление пара растворителя над раствором становится равным давлению пара над твердой фазой, называется температурой кристаллизации раствора (Tкр.).
Температура, при которой давление пара растворителя над раствором становится равным атмосферному давлению, назы-вается температурой кипения раствора (Tкип.).
Из рис. 1 видно, что температура кристаллизации раствора (Tкр.) несколько ниже температуры кристаллизации чистого растворителя (T0 кр.). Разность температур кристаллизации растворителя и раствора DTкр.можно рассчитать по одному из следствий из закона Рауля:
Понижение температуры кристаллизации раствора по сравнению с растворителем прямо пропорционально моляльной концентрации раствора:
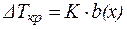 , ,
| (2) |
где К – криоскопическая постоянная растворителя (К×кг/моль);
b(х) – моляльная концентрация раствора (моль/кг).
Другое следствие из закона Рауля позволяет рассчитать повышение температуры кипения раствора по сравнению с растворителем DTкип.:
Повышение температуры кипения раствора по сравнению с растворителем прямо пропорционально моляльной концентрации раствора:
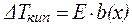 , ,
| (3) |
где Е – эбулиоскопическая постоянная растворителя (К×кг/моль).
Значения констант К и Е определяются исключительно природой растворителя.
Значения криоскопических и эбулиоскопических констант некоторых растворителей приведены в таблице 1.
Таблица 1. Физико-химические характеристики растворителей.
| Растворитель | Температура кипения, 0С | Температура кристал-лизации, 0С | Эбулиоско-пическая константа, К×кг/моль. | Криоско-пическая константа, К×кг/моль. |
| Вода | 0,52 | 1,86 | ||
| Бензол | 80,1 | 5,5 | 2,56 | 5,10 |
| Этанол | 78,4 | -114,15 | 1,16 | 1,99 |
| Ацетон | 56,2 | -95,35 | 1,50 | 2,40 |
| Хлороформ | 61,2 | -63,5 | 4,90 | 3,90 |
| Диэтиловый эфир | 34,5 | -116,2 | 2,02 | 1,79 |
| Камфора | 5,95 | 39,7 |
Следствия из закона Рауля позволяют также решить и обратную задачу: зная величину DTкип. (или DTкр.) можно рассчитать молярную массу растворенного вещества M(x):
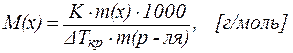
| (4) |
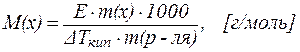
| (5) |
Диффузия и осмос
Процесс самопроизвольного выравнивания концентраций веществ в термодинамической системе называют диффузией.
Диффузия является двусторонним процессом. Так, в растворах в процессе диффузии участвуют как молекулы растворителя, так и молекулы (ионы) растворенных веществ.
Процесс преимущественно одностороннего проникновения молекул растворителя через полупроницаемую мембрану называют осмосом.
В процессе осмоса, молекулы растворителя проникают через полупроницаемую мембрану либо из растворителя в раствор, либо из разбавленного раствора в более концентрированный.
Явление осмоса схематично представлено на рис. 2, из которого видно, что в процессе осмоса уровень жидкости в объеме с раствором глюкозы повышается. При этом создается дополнительное гидро-статическое давление, препятствующее дальнейшему проникновению растворителя через мембрану.
Дополнительное гидростатическое давление, при котором осмос прекращается, называют осмотическим давлением.
Осмотическое давление обозначают буквой p и выражают в кПа или в атм.
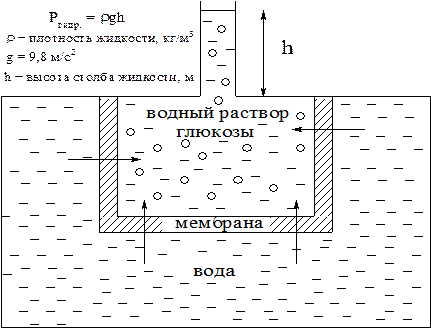
Рис. 2. Явление осмоса.
Изучая осмотические явления, Вант-Гофф установил их полную аналогию с законами поведения идеальных газов.
Закон Вант-Гоффа:
Осмотическое давление разбавленных растворов неэлектро-литов прямо пропорционально молярной концентрации раствора и абсолютной температуре:
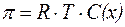
| (6) |
где С(х) - молярная концентрация раствора, моль/л;
R - газовая постоянная (8,31 Дж/(моль×К); 0,082 л×атм/(моль×K));
Т - абсолютная температура (К).
Интересно отметить, что даже при сравнительно небольших кон-центрациях, растворы могут обладать значительным осмотическим давлением. Так, осмотическое давление одномолярного раствора глюкозы при 00С составляет 22,4 атм.
Растворы электролитов
Из рис. 1 видно, что при равных концентрациях растворов дав-ление насыщенного пара растворителя над раствором электролита (кривая 3) ниже, чем над раствором неэлектролита той же концентра-ции (кривая 2). Это объясняется тем, что диссоциация электролита приводит к увеличению общего числа частиц растворенного вещества. Вследствие сольватации образовавшихся ионов умень-шается количество свободных молекул растворителя на поверхности раздела жидкость-пар. Таким образом, свойства, зависящие от общего числа находящихся в растворе частиц растворенного вещества (коллигативные свойства), проявляются в растворах электролитов в большей степени, чем в равных им по концентрации растворах неэлектролитов.
Если в результате диссоциации общее число частиц в растворе электролита возросло в i раз по сравнению с числом его молекул, то это должно быть учтено при расчете коллигативных свойств:
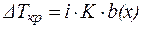 , ,
| (7) |
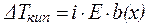
| (8) |
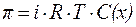
| (9) |
где i – изотонический коэффициент (коэффициент Вант-Гоффа).
Изотонический коэффициент i связан со степенью диссоциации электролита a следующим соотношением:
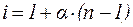 , ,
| (10) |
где n – число ионов, на которые при диссоциации распадается электролит.
Пример 1. Рассчитать изотонический коэффициент Вант-Гоффа для АlСl3, если «кажущаяся» степень диссоциации 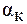 = 80%.
= 80%.
Решение.
В растворе сильного электролита изотонический коэффициент рассчитывается по формуле:
i = 1 + 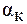 ∙(n – 1).
∙(n – 1).
Степень диссоциации 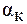 выражается в долях единицы и равна 0,8. Для расчета n, т.е. числа ионов, на которые диссоциирует электролит, необходимо написать уравнение диссоциации:
выражается в долях единицы и равна 0,8. Для расчета n, т.е. числа ионов, на которые диссоциирует электролит, необходимо написать уравнение диссоциации:
AlCl3  Al3+ + 3Cl-
Al3+ + 3Cl-
Таким образом:
n = 4,
i = 1 + 0,8×(4 – 1) = 3,4.
По опытным величинам p, DTкип. и DTкр. можно определить значение i, что, в свою очередь, позволяет вычислить степень диссоциации электролита в растворе. При этом следует иметь в виду, что в случае сильных электролитов найденное таким образом значение 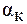 выражает лишь «кажущуюся» степень диссоциации, поскольку в растворах сильные электролиты диссоциированы полностью. Наблюдаемое отличие «кажущейся» степени диссоци-ации от единицы связано с межионным взаимодействием в растворе.
выражает лишь «кажущуюся» степень диссоциации, поскольку в растворах сильные электролиты диссоциированы полностью. Наблюдаемое отличие «кажущейся» степени диссоци-ации от единицы связано с межионным взаимодействием в растворе.
Биологическое значение осмотического давления
Осмос играет большую роль в существовании растительных и животных организмов, способствуя достаточному наполнению водой клеток и межклеточных структур. Животные и растительные клетки в составе своей оболочки имеют полупроницаемые мембраны и могут рассматриваться как миниатюрные осмотические системы. Так, оболочка эритроцитов непроницаема для ряда катионов (например, для К+, Na+) и свободно пропускает анионы и воду.
Возникающее при этом осмотическое давление обуславливает тургор клеток (от лат. turgor - вздутие, наполнение), т. е. внутреннее гидростатическое давление в живой клетке, вызывающее напряжение клеточной оболочки. У животных тургор клеток обычно невысок, а у растений варьируется от 5-20 атм до 120-140 атм (у растений засушливых районов). Более высокое (по сравнению с грунтовыми водами) осмотическое давление клеток растений обеспечивает процесс всасывания воды корнями растений и дальнейший ее подъем на значительную высоту. Тургорным действием объясняется также набухание семян растений, явление «пробивания» растущими побегами земли и других препятствий, поддержание листьев и стеблей (у травянистых растений) в вертикальном положении.
Наличие воды в клетках и тканях необходимо и для протекания многообразных физических и химических процессов: гидратации и диссоциации веществ, реакций гидролиза, окисления и т. п. Иначе говоря, тургор - это показатель состояния водного режима клеток. Снижение тургора приводит к старению и увяданию клеток.
Растворы с равным осмотическим давлением, называются изотоническими. Если два раствора имеют различное осмотическое давление, то раствор с большим давлением называются гипертони-ческим, с меньшим давлением - гипотоническими.
Пример 2. Не прибегая к расчетам, указать, какие из растворов при одинаковой температуре являются изотоническими:
а) С(NaCl) = 0,03 моль/л, a = 1 и С(С6Н12О6) = 0,03 моль/л;
б) С(CO(NH2)2) = 0,03 моль/л и С(СаС12) = 0,01 моль/л, 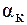 = 1.
= 1.
Решение.
Для растворов электролитов:
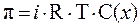 ,
,
для неэлектролитов i = l, следовательно:
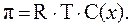
Для каждой пары растворов RT = const, следовательно, достаточно сравнить множитель i×С(x) в каждой паре растворов.
а) 2×0,3 ¹ 0,3 (неизотоничны);
б) 0,3 = 3×0,1 (изотоничны).
Очевидно, что изотонические растворы содержат одинаковое ко-личество осмотически активных частиц. Активную концентрацию частиц, не проникающих через идеальную полупроницаемую мембра-ну, выражают через осмолярность (осмоляльность).
Осмолярностью (осмоляльностью) раствора называется суммарная концентрация всех кинетически активных частиц в растворе, определяющих его осмотическое давление.
Математически величины осмолярности и осмоляльности рассчитываются следующим образом:
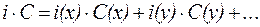
| (11) |
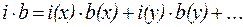
| (12) |
Единицы измерения этих величин совпадают с единицами измерения молярной и моляльной концентрации, соответственно. В медицинской литературе эти величины принято выражать в Осмоль/л и Осмоль/кг.
В разбавленных водных растворах осмолярность и осмоляльность приблизительно равны.
Пример 3. Рассчитать осмолярность клеток саксаула, если осмотическое давление при 300С равно 145 атм.
Решение.
Осмолярность раствора определим по формуле:
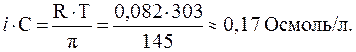
Если поместить животные или растительные клетки в гипотони-ческий раствор, то произойдет перемещение воды внутрь клеток, что приведет к их набуханию, а затем, возможно, к разрыву оболочек и вытеканию клеточного содержимого (рис. 3.). Подобное разрушение клеток называется лизисом,а в случае эритроцитов - гемолизом.
В гипертонических растворах происходит сморщивание клеток (плазмолиз), обусловленное потерей воды, перемещающейся из них во внешний раствор.
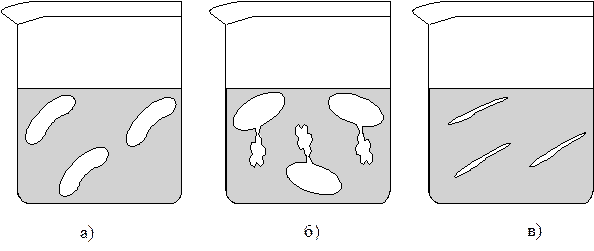
Рис. 3. Изменения, происходящие с кровяными тельцами в растворах NaCl различной концентрации:
а – изотонический раствор NaCl (0,9%);
б – гипотонический раствор NaCl (0,1%);
в – гипертонический раствор NaCl (2%).
Пример 3. Что произойдет с растительной клеткой, осмотическое давление внутри которой pкл составляет 20 атм, если ее поместить в раствор с pр-ра = 30 атм?
Решение.
Так как p(р-ра) > p(клетки), следовательно, раствор гипер-тонический. Наблюдается сморщивание (плазмолиз) клетки за счет перемещения воды из клетки в раствор.
Осмотическое давление биологических жидкостей, отвечающее состоянию тургора, у разных живых организмов неодинаково. Так, некоторые морские животные имеют осмотическое давление крови выше, чем у человека. Это связано с обитанием этих животных в среде с высоким содержанием солей. Обитатели же пресноводных водоемов, например, лягушки, имеют осмотическое давление крови ниже, чем у человека.
Биологические жидкости человека - тканевые жидкости, кровь, лимфа, - представляют собой водные растворы низкомолекулярных соединений (NaCl, KCl, CaCl2), высокомолекулярных соединений (белков, полисахаридов, нуклеиновых кислот) и форменных элементов (в крови - это эритроциты, лейкоциты, тромбоциты).
Их суммарное осмотическое давление определяет тургор клеток. Так, осмотическое давление кровяных эритроцитов человека составляет 7,6-7,9 атм. Такое же осмотическое давление создает и 0,9%-й (С(NaCl) = 0,15 моль/л) раствор NaCl (физиологический раствор), являющийся, следовательно, изотоничным крови.
Существенную часть крови составляют белки, представленные в основном дыхательными пигментами, белками стромы эритроцитов и белками других форменных элементов. Белки, растворённые в плазме (6,5-8,5% из 9-10% сухого остатка плазмы), образуются преимущест-венно в клетках печени и ретикулоэндотелиальной системы. Белки плазмы крови не проникают через стенки капилляров, поэтому содер-жание их в плазме значительно выше, чем в тканевой жидкости. Это приводит к удержанию воды белками плазмы.
Часть осмотического давления крови, создаваемая белками (альбумины, глобулины), называется онкотическим давлением. Онкотическое давление равно 0,04 атм, что составляет прибли-зительно 0,5% от общего осмотического давления крови.
Несмотря на то, что онкотическое давление составляет лишь небольшую часть общего осмотического давления крови, именно оно обуславливает преобладание осмотического давления крови над осмотическим давлением тканевой жидкости. При иных условиях в результате высокого гидродинамического давления в кровеносной системе вода просачивалась бы в ткани, что вызывало бы возник-новение отёков различных органов и подкожной клетчатки.
Падение осмотического давления в клетках при обезвоживании организма приводит к их коллапсу (плазмолизу); наоборот, обес-соливание организма приводит к набуханию и разрыву клеток (осмотический шок). Шок при сильных кровотечениях обусловлен не столько потерей крови, сколько резким падением осмотического давления и коллапсом сосудов. Поэтому при больших потерях крови пострадавшим вводят инертные высокомолекулярные заменители плазмы крови (например, раствор поливинилпирролидона), благодаря которым восстанавливается тургор и устраняется шок.
Эталоны решения задач
Примечание. При расчете Dtкр. и Dtкип. следует помнить, что 10 по шкале Цельсия равен 10 по шкале Кельвина, поэтому любая конечная разность температур может быть представлена как в 0C, так и в К без соответствующего пересчета.
1. Вычислить температуру кипения и температуру кристал-лизации водного раствора мочевины, содержащего 6 г CO(NH2)2 в 100 г воды, если К(H2O) = 1,86 К×кг/моль, E(H2O) = 0,52 К×кг/моль.
Решение.
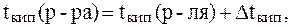
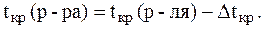
Известно, что:
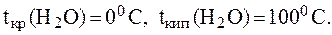
Для раствора неэлектролита:
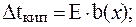

Моляльная концентрация раствора равна:
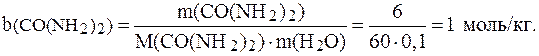
Таким образом:
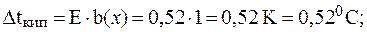 *
*
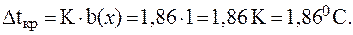
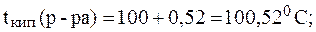
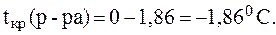
2. Вычислить температуру кипения и температуру кристал-лизации 10% раствора сульфата натрия, если 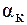 = 55%.
= 55%.
Решение.
Для раствора электролита:
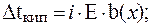
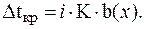
Если массовая доля раствора равна 10%, то это означает, что в 100 г раствора содержится 10 г вещества и 90 г воды.
Тогда:
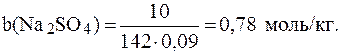
Изотонический коэффициент рассчитаем по формуле (10):
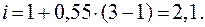
Таким образом:

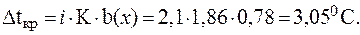
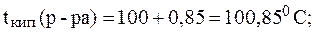
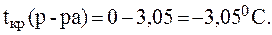
3. При растворении 0,029 моль неэлектролита в 100 г ацетона температура кипения раствора повысилась на 0,4350С. Вычислить эбулиоскопическую константу ацетона.
Решение.
Согласно следствию из закона Рауля:
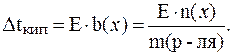
Отсюда:
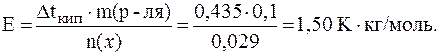
4. В равных объемах эфира растворены одинаковые массы бензойной кислоты (C6H5COOH) и анилина (C6H5NH2). Определить, какой из растворов кипит при более высокой температуре.
Решение.
Согласно следствию из закона Рауля:


Разделим одно выражение на другое и получим:
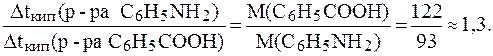
Таким образом, 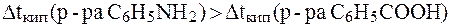 , следовательно, раствор анилина кипит при более высокой темпе-ратуре.
, следовательно, раствор анилина кипит при более высокой темпе-ратуре.
5. Найти массу фенола C6H5OH, которую необходимо растворить в 200 мл бензола, чтобы снизить температуру кристаллизации раствора до 50C, если для бензола: r = 0,87 г/мл, К = 5,1 К×кг/моль, 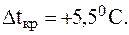
Решение.
Согласно следствию из закона Рауля:
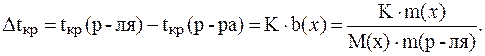
Массу растворителя найдем из соотношения:
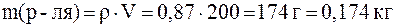 .
.
Отсюда:
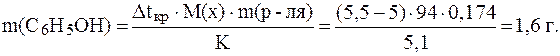
6. Определить, что произойдет с растительной клеткой, осмоти-ческое давление внутри которой 5 атм, если ее поместить в раствор глюкозы c w(С6Н12О6) = 1,8% плотностью 1 г/мл при 170С.
Решение.
Согласно закону Вант-Гоффа, осмотическое давление раствора p пропорционально молярной концентрации раствора. Поэтому следует выразить концентрацию раствора в моль/л:
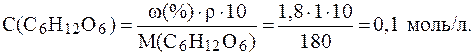
Так как глюкоза является неэлектролитом, осмотическое давление раствора находим по формуле (6):
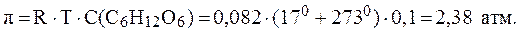
Так как p(раствора) < p(клетки), следовательно, раствор глюкозы является гипотоническим по отношению к клетке и будет проис-ходить набухание клетки.
7. Найти молярную концентрацию раствора неэлектролита, если осмотическое давление этого раствора при 170С равно 482 кПа.
Решение.
В растворе неэлектролита С(x) найдем, используя формулу (6):
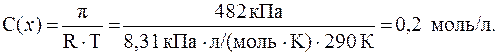
8. Определить, как и во сколько раз изменится осмотическое давление раствора неэлектролита, если температуру раствора повы-сить от 17 до 470С (изменением объема при нагревании пренебречь).
Решение.
Согласно закону Вант-Гоффа, осмотическое давление раствора p увеличивается с ростом температуры. При условии равенства концен-траций можно записать:
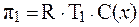 ;
;
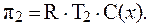
Отсюда:
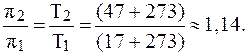
Таким образом, осмотическое давление увеличилось в 1,14 раз.
9. Найти, в каком объемном соотношении следует развести раствор с осмотическим давлением 1,6 МПа водой, чтобы снизить осмотическое давление раствора до 0,4 МПа.
Решение.
Так как T и R = const:
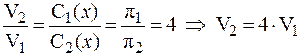 .
.
При разведении раствора:
V2 = V1 + V(H2O).
Отсюда:
V(H2O) = 4×V1 - V1 = 3×V1.
Таким образом, раствор следует развести водой в объемном соотношении 1:3.
10. Рассчитать осмотическое давление водного раствора глюкозы при 170С, если понижение температуры кристаллизации этого раствора составляет 3,720.
Решение.
Глюкоза - неэлектролит, поэтому:
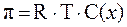 ,
,

Учитывая, что для разбавленных водных растворов b(х) » С(х), из второго уравнения выразим b(х) и подставим в первое:
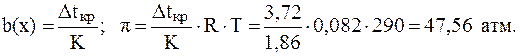
11. Температура кипения раствора, содержащего 0,4 г серы в 50 г бензола, на 0,080С выше температуры кипения чистого бензола. Уста-новить молекулярную формулу серы, если Е(C6H6) = 2,56 К×кг/моль.
Решение.
Обозначим молекулу серы Sn и запишем соответствующее следствие из закона Рауля:
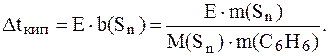
Отсюда:
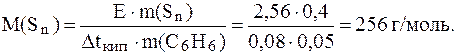
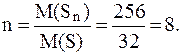
Таким образом, молекула серы имеет формулу S8.
12. Определить молярную массу поливинилпирролидона (ПВП), применяемого в качестве заменителя плазмы крови, если при 200С осмотическое давление раствора, содержащего 1 г ПВП в 100 мл воды составляет 20 мм. рт. ст.
Решение.
Выразим объем раствора в л, а осмотическое давление в кПа:
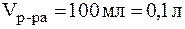 ;
;
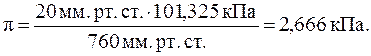
Согласно закону Вант-Гоффа:
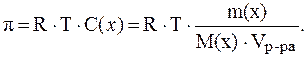
Отсюда:

13. Вычислить изотонический коэффициент для раствора электролита с молярной концентрацией 0,001 моль/л, если в 500 мл этого раствора содержится 3,4×1020 частиц (молекул и ионов) растворенного вещества.
Решение.
Изотонический коэффициент показывает, во сколько раз возрастает число активных частиц при диссоциации растворенного вещества: i = N/N0.
Для приготовления 500 мл раствора был взят электролит, число молекул которого N0 равно:
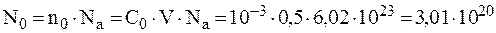 .
.
Таким образом:
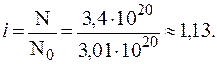
14. Раствор, содержащий 0,85 г ZnCl2 в 125 г воды, кристалли-зуется при -0,230С. Вычислить кажущуюся степень диссоциации 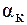 .
.
Решение.
В растворе электролита кажущуюся степень диссоциации 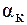 можно найти, зная величину изотонического коэффициента, который, в свою очередь, можно рассчитать по формуле:
можно найти, зная величину изотонического коэффициента, который, в свою очередь, можно рассчитать по формуле:
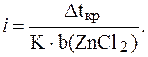
Определим 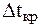 раствора:
раствора:
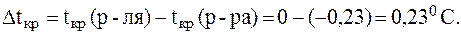
Найдем b(х) соли в растворе:
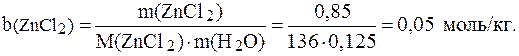
Отсюда:
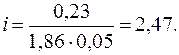
Таким образом:
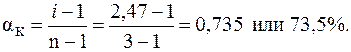
15. Рассчитать температуру кристаллизации и осмотическое давление раствора молочной кислоты с концентрацией 0,02 моль/л при 350С, если 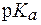 (CH3CH(OH)COOH) = 4.
(CH3CH(OH)COOH) = 4.
Решение.
В растворе слабой одноосновной кислоты степень диссоциации можно рассчитать по закону Оствальда*:
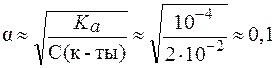 .
.
Изотонический коэффициент найдем по уравнению (10):
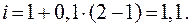
Осмотическое давление раствора рассчитаем по формуле (9):
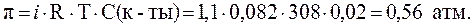
Относительное понижение температуры кристаллизации найдем по уравнению (7), учитывая, что b(х) » С(х):
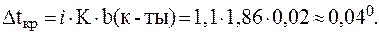
Отсюда:
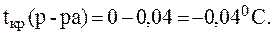
*Молочная кислота - электролит средней силы, поэтому более точный расчет величины a следует проводить по уравнению:
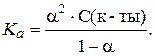
Решая квадратное уравнение:
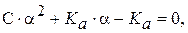
получим:
a » 0,07.
16. 1 л инкубационного раствора, идентичного по составу влаге передней стенки глаза, содержит 104,32 ммоль NаCl, 27,26 ммоль NaHCO3, 4,08 ммоль KHCO3, 0,79 ммоль MgCl2, 1,77 ммоль глюко-ната кальция, 5,55 ммоль глюкозы; 0,59 ммоль K2SO4, 0,56 ммоль аскорбиновой кислоты ( 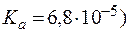 , 0,28 ммоль Nа2НРО4, и имеет рН = 7,4. Рассчитать осмолярность данного раствора.
, 0,28 ммоль Nа2НРО4, и имеет рН = 7,4. Рассчитать осмолярность данного раствора.
Решение.
Осмолярность рассчитывается как сумма произведений изотонических коэффициентов на молярные концентрации всех компонентов раствора:
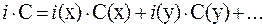
В данном растворе присутствуют сильные электролиты (NаCl, NaHCO3, MgCl2 и др.), слабые электролиты (аскорбиновая кислота) и неэлектролиты (глюкоза).
Так как концентрации сильных электролитов в растворе малы, то величину 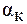 можно принять равной 1 и считать, что i = n. Таким образом, для бинарных сильных электролитов (NаCl, NaHCO3, KHCO3) i = 2, для всех остальных (MgCl2, K2SO4, Nа2НРО4 и глюко-ната кальция) i = 3.
можно принять равной 1 и считать, что i = n. Таким образом, для бинарных сильных электролитов (NаCl, NaHCO3, KHCO3) i = 2, для всех остальных (MgCl2, K2SO4, Nа2НРО4 и глюко-ната кальция) i = 3.
Диссоциацией таких слабых электролитов как HCO3- и НРО42- можно пренебречь ввиду малых величин констант диссоциации (5,0×10-11 и 3,5×10-13, соответственно).
Так как при рН = 7,4 концентрации ионов H+ и OH- ~ 10-7 моль/л, то ими также можно пренебречь.
Степень диссоциации аскорбиновой кислоты найдем по формуле закона Оствальда:
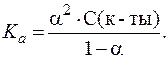
Решая квадратное уравнение:
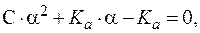
получим:
a » 0,3,
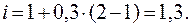
Таким образом, осмолярность раствора равна:
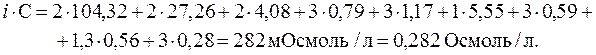
Вопросы для самоконтроля
1. Какие свойства растворов называются коллигативными? Приведите примеры.
2. Что такое насыщенный пар? Какие характеристики насыщен-ного пара вы знаете?
3. Как давление насыщенного пара растворителя зависит от температуры? Изобразите эту зависимость схематично. Укажите точки, соответствующие фазовым превращениям.
4. Почему давление насыщенного пара растворителя над раствором нелетучего неэлектролита ниже давления насыщенного пара над чистым растворителем? Как это выглядит на графике?
5. Сформулируйте закон Рауля. Какие следствия из него вы знаете?
6. От чего зависят значения эбулиоскопической и криоско-пической констант? Какова их размерность? В чем заключается физический смысл этих констант?
7. Что такое диффузия? Что такое осмос? В чем заключается сходство и в чем различие этих процессов?
8. Что такое осмотическое давление? Как формулируется гидро-статическая интерпретация этого термина?
9. По какой формуле вычисляется осмотическое давление? От чего зависит значение осмотического давления раствора? В каких единицах выражается осмотическое давление?
10. Что такое изотонический коэффициент? Как он рассчи-тывается?
11. Какова биологическая роль осмоса? Приведите примеры применения осмоса в повседневной жизни и в лечебных целях.
12. Какие растворы называют изотоничными? Что представляет собой физиологический раствор?
13. Какие растворы называют гипертоническими? Какие гипо-тоническими?
14. Что такое плазмолиз, лизис, гемолиз?
15. Почему для растений, хорошо переносящих холод и засуху, характерна высокая концентрация веществ в клетке?
Варианты задач для самостоятельного решения
Примечание. Значения криоскопических и эбуллиоскопических констант, а также температуры кипения и кристаллизации растворителей, приведены в таблице 1.
Вариант №1
1. Вычислить температуру кипения и температуру кристалли-зации раствора, содержащего 1,5 г нафталина (C10H8) в 50 г бензола.
2. Определить, что произойдет с клеткой, осмотическое давление внутри которой 7 атм, если ее поместить в раствор сахарозы с w(С12Н22О11) = 6% плотностью 1,05 г/мл при 200C.
3. Раствор, содержащий 2,22 г СаСl2 в 100 г воды, кристаллизует-ся при -0,930С. Рассчитать кажущуюся степень диссоциации СаСl2 и осмотическое давление раствора при 150C, если rр-ра » 1 г/мл.
Вариант №2
1. Вычислить температуру кипения и температуру кристалли-зации 5% водного раствора NaCl, если aк = 80%.
2. Определить, что произойдет с клеткой, осмотическое давление внутри которой 3,5 атм, если ее поместить в раствор сульфата железа (III) с w(Fe2(SO4)3) = 2% (r = 1,1 г/мл, 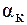 = 80%) при 250С.
= 80%) при 250С.
3. Раствор, содержащий 13 г неэлектролита в 400 г диэтилового эфира, кипит на 0,4530С выше по сравнению с чистым растворителем. Вычислить молярную массу растворенного вещества и осмотическое давление раствора при 100C, если rр-ра = 0,75 г/мл.
Вариант №3
1. Рассчитать массу С12Н22О11, которую необходимо растворить в 100 мл воды, чтобы:
а) понизить температуру кристаллизации раствора на 10С;
б) повысить температуру кипения раствора на 0,40С.
2. Определить, что произойдет с клеткой, осмотическое давление внутри которой 7 атм, если ее поместить в раствор хлорида калия c w(KCl) = 7,5% (r = 1,1 г/мл, 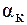 = 70%) при 220C.
= 70%) при 220C.
3. В 200 мл раствора содержится 2,8 г высокомолекулярного соединения. При 250С осмотическое давление этого раствора составляет 0,7 Па. Найти молярную массу полимера.
Вариант №4
1. Вычислить температуру кипения и температуру кристалли-зации раствора, содержащего 12 г глюкозы (C6H12O6) в 200 мл воды.
2. Рассчитать количество растворенного вещества (неэлектро-лита) в 100 мл раствора, осмотическое давление которого при 200С составляет 245 кПа.
3. Температура кристаллизации водного раствора мочевины составляет -0,3720С. Рассчитать осмотическое давление данного раствора при 130C если rр-ра » 1 г/мл.
Вариант №5
1. Раствор, содержащий 100 г ацетона и 2,3 г глицерина, кипит при 56,580С, а кристаллизуется при -95,350С. Вычислить K и E ацетона.
2. К 100 мл водного раствора мочевины с молярной концен-трацией 0,5 моль/л добавили 400 мл воды и понизили температуру от 25 до 50С. Определить, как во сколько раз изменится осмотическое давление раствора.
3. Температура кипения спиртового раствора иода, содержащего 8,8 г иода в 200 г этанола, составляет 78,60С. Установить молекуляр-ную формулу иода.
Вариант №6
1. Рассчитать температуру кипения и температуру кристалли-зации водного раствора хлорида алюминия с C( 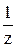 AlCl3) = 0,1 моль/л, если
AlCl3) = 0,1 моль/л, если 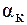 = 65%.
= 65%.
2. Найти массу глюкозы в 0,2 л раствора, осмотическое давление которого при 370С составляет 810 кПа.
3. Понижение температуры кристаллизации раствора, содержа-щего 0,3 г СН3СООН в 50 г воды, равна 0,1880С. Найти степень диссоциации уксусной кислоты и осмотическое давление раствора при 270C, если rр-ра » 1 г/мл.
Вариант №7
1. Вычислить температуру кипения и температуру кристалли-зации 10%-го водного раствора глицерина (C3H8O3).
2. Определить, что произойдет с клеткой, осмотическое давление внутри которой 7,6 атм, если ее поместить в раствор хлорида натрия c w(NaCl) = 0,87% (r = 1,06 г/мл, 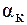 = 90%) при 370C.
= 90%) при 370C.
3. Раствор, содержащий 2,1 г КОН в 250 г воды, кристаллизуется при -0,5190С. Рассчитать кажущуюся степень диссоциации КОН и осмотическое давление раствора при 00C, если rр-ра » 1 г/мл.
Вариант №8
1. Рассчитать массу мочевины СО(NН2)2, которую необходимо растворить в 200 мл воды, чтобы:
а) понизить температуру кристаллизации раствора на 10С;
б) повысить температуру кипения раствора на 0,350С.
2. Найти, в каком объемном соотношении следует развести раствор с осмотическим давлением 2,5 МПа водой, чтобы снизить осмотическое давление раствора до 0,5 МПа.
3. Водный раствор, содержащий 15% неэлектролита, кристал-лизуется при -5,60С. Вычислить молярную массу неэлектролита и осмотическое давление раствора, если rр-ра = 1,1 г/мл.
Вариант №9
1. Рассчитать температуру кипения и температуру кристаллиза-ции водного раствора хлорида магния с C( 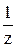 MgCl2) = 0,1 моль/л, если
MgCl2) = 0,1 моль/л, если 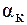 = 75%.
= 75%.
2. Определить, как и во сколько раз изменится осмотическое дав-ление раствора неэлектролита, если температуру раствора повысить от 5 до 350С.
3. Определить, изотоничны ли при одинаковой температуре водные растворы иодида калия с С(КI) = 0,1 моль/л, ( 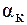 = 85%) и глюкозы, который кристаллизуется при -0,3720С и имеет плотность 1,05 г/мл.
= 85%) и глюкозы, который кристаллизуется при -0,3720С и имеет плотность 1,05 г/мл.
Вариант №10
1. Вычислить температуру кипения и температуру кристал-лизации раствора, содержащего 2,5 г фенола (C6H5OH) в 90 г бензола.
2. Определить, что произойдет с клеткой, осмотическое давление внутри которой 15 атм, если ее поместить в раствор хлорида кальция c w(СaCl2) = 10% (r = 1,1 г/мл, 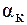 = 80%) при 300C.
= 80%) при 300C.
3. Осмотическое давление раствора, содержащего 9 г маннита (неэлектролит) в 250 мл раствора, при 00С составляет 456 кПа. Рассчитать молярную массу маннита.
Вариант №11
1. Рассчитать, сколько г глюкозы С6Н12О6 следует растворить в 250 мл воды, чтобы:
а) понизить температуру кристаллизации раствора на 1,50С;
б) повысить температуру кипения раствора на 0,250С.
2. Определить температуру, при которой должен находиться раствор, содержащий 0,35 моль неэлектролита в 1 л раствора, чтобы быть изотоничным раствору, содержащему при 200С 6,2 г этилен-гликоля в 250 мл раствора.
3. Температура кипения раствора, содержащего 13 г камфоры (неэлектролит) в 400 г диэтилового эфира, составляет 34,950С. Вычислить молярную массу камфоры и осмотическое давление раствора при 50С, если rр-ра » 1 г/мл.
Вариант №12
1. Найти массу AgNO3 в 50 мл воды, если известно, что данный раствор кристаллизуется при -0,3720С, а 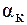 = 60%.
= 60%.
2. Вычислить, при какой температуре осмотическое давление раствора, содержащего 36 г глюкозы в 1 л, достигнет 520 кПа.
3. При 200С осмотическое давление раствора, содержащего 1,2 г неэлектролита в 200 мл водного раствора, составляет 243,18 кПа. Вычислить молярную массу неэлектролита, температуру кипения и температуру кристаллизации раствора, если rр-ра » 1 г/мл.
Вариант №13
1. В равных объемах воды растворены одинаковые массы сахаро-зы (М = 342 г/моль) и альбумина (М = 68000 г/моль). Определить, какой из растворов кристаллизуется при более низкой температуре.
2. В равных объемах бензола растворены одинаковые массы нафталина (C10H8) и антрацена (C14H10). Определить, как и во сколько раз отличаются значения осмотического давления этих растворов.
3. Определить, изотоничны ли водные растворы хлорида кальция с C(СаСl2) = 0,1 моль/л ( 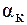 = 100%) и водный раствор мочевины, который кристаллизуется при -0,5580С и имеет плотность 1,05 г/мл.
= 100%) и водный раствор мочевины, который кристаллизуется при -0,5580С и имеет плотность 1,05 г/мл.
Вариант №14
1. Вычислить температуру кипения и температуру кристаллиза-ции раствора, содержащего 500 г этиленгликоля (C2H6O2) в 4 л воды.
2. Определить, что произойдет с клеткой, осмотическое давление внутри которой 2,5 атм, если ее поместить в раствор карбоната натрия с w(Na2CO3) = 10% (r = 1,06 г/мл, 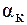 = 75%) при 170C.
= 75%) при 170C.
3. Раствор, содержащий 3,24 г серы в 40 г бензола, кипит на 0,810С выше, чем чистый растворитель. Определить молекулярную формулу серы.
Вариант №15
1. Рассчитать температуру кипения и температуру кристал-лизации водного раствора сульфата меди с w(CuSO4) = 0,8%, если 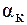 = 40%.
= 40%.
2. При одной и той же температуре раствор, содержащий 3,7 г глюкозы в 0,5 л раствора, изотоничен раствору мочевины. Найти массу мочевины в 1 л раствора.
3. Раствор, содержащий 42 г неэлектролита в 420 г воды, кипит при 100,250С. Определить молярную массу растворенного вещества и осмотическое давление раствора при 350С, если rр-ра = 1,1 г/мл.
Вариант №16
1. Вычислить температуру кипения и температуру кристаллиза-ции раствора, содержащего 1 г нитробензола (C6H5NO2) в 10 г бензола.
2. Определить, будут ли при одинаковой температуре изото-ничны растворы сахара (С12Н22О11) и глюкозы (С6Н12О6), с концен-трациями, равными, соответственно, 0,5 моль/л и 30 г/л.
3. Раствор, содержащий 4,11 г KNO3 в 100 мл воды, кипит при 100,3980С. Рассчитать 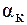 (KNO3) и осмотическое давление раствора при 180С, если rр-ра = 1,05 г/мл.
(KNO3) и осмотическое давление раствора при 180С, если rр-ра = 1,05 г/мл.
Вариант №17
1. Вычислить температуру кипения и температуру кристаллиза-ции раствора, содержащего 15 г хлороформа (CHCl3) в 400 г диэтилового эфира.
2. Рассчитать осмотическое давление раствора пировиноградной кислоты с концентрацией 0,025 моль/л при 250С, если 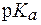 = 2,5.
= 2,5.
3. В равных объемах воды растворены 0,5 моль СаСl2 и 0,2 моль сахара (С12Н22О11). Найти кажущуюся степень диссоциации СаСl2, если температуры кристаллизации обоих растворов одинаковы.
Вариант №18
1. Раствор, содержащий 2,5 г ДМСО ((CH3)2SO) в 90 г бензола кипит при 81,010С, а кристаллизуется при 3,680С. Найти K и E бензола.
2. Вычислить массу глюкозы в 1 л раствора, если известно, что при одинаковой температуре этот раствор изотоничен формалину, содержащему 1,5 г формальдегида в 0,5 л раствора.
3. Понижение температуры кристаллизации водного раствора, содержащего 1,5 г неэлектролита в 50 мл воды, составляет 0,930С. Рассчитать молярную массу неэлектролита и осмотическое давление раствора при 220С, если rр-ра » 1 г/мл.
Вариант №19
1. Рассчитать массу KOH, которую следует растворить в 350 мл воды, чтобы:
а) понизить температуру кристаллизации раствора на 0,5580С;
б) повысить температуру кипения раствора на 0,1560С.
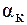 (KOH) = 90%.
(KOH) = 90%.
2. Вычислить изотонический коэффициент для раствора электролита с молярной концентрацией 0,01 моль/л, если в 1 л этого раствора содержится 6,45×1021 частиц (молекул и ионов) растворен-ного вещества.
3. Раствор, содержащий 2 г серы в 40 г бензола кристаллизуется при 4,50С. Установить молекулярную формулу серы.
Вариант №20
1. Экспериментально установлено, что водные растворы этилен-гликоля с концентрациями 52,6% и 66% кристаллизуются, соответст-венно, при температурах -400С и -650С. Рассчитать значения температур кристаллизации этих растворов при помощи следствий из закона Рауля и объяснить причину наблюдаемых различий между теоретически рассчитанными и экспериментально измеренными значениями температур кристаллизации растворов.
На основании имеющихся данных сделать вывод: можно ли использовать 40% водный раствор этиленгликоля в качестве антифриза при -200С?
2. При 200С смешали два раствора неэлектролита: 1 л раствора с p = 400 кПа и 2 л раствора с p = 250 кПа. Вычислить осмотическое давление полученного раствора.
3. Раствор 2,13 г неизвестного вещества в 60 г бензоле не проводит ток и кристаллизуется при 4,250С. Установить формулу вещества, если массовые доли элементов составляют: 50,69% углерода, 4,23% водорода и 45,08% кислорода.
БЛОК ИНФОРМАЦИИ
буферные системы
Функциональное состояние живых организмов неразрывно связа-но с постоянством активной реакции среды тканей, органов и ряда биологических жидкостей (крови, слюны, желудочного сока и др.), определяемой водородным показателем (рН). Состояние кислотно-основного равновесия, соответствующее норме, называется протоли-тический гомеостаз. Смещение протолитического равновесия в кис-лую область (снижение рН) вызывает ацидоз, в щелочную (повыше-ние рН) - алкалоз. Возникновение этих отклонений может быть выз-вано разными причинами.
Например, в процессе метаболических превращений в клетках организма образуются кислоты (угольная, серная, фосфорная, молочная и др.) и основания (аммиак, азотистые основания). Выделе-ние этих веществ в количествах, превышающих допустимую норму, может привести к ацидозу или алкалозу.
В процессе тканевого дыхания в организме высвобождается большое количество углекислого газа. Транспорт СО2 осуществля-ется кровью, которая представляет собой одну из важнейших внут-ренних сред организма и характеризуется определенным диапазоном колебаний рН – от 7,37 до 7,45 со средней величиной 7,38-7,40. Даже небольшие отклонения рН крови от нормы свидетельствуют о патологических нарушениях метаболизма. Величины рН крови ниже 6,8 и выше 7,8 несовместимы с жизнью.
Присутствие кислотных оксидов (таких как СО2) может вызвать сдвиг значений рН раствора в область более низких значений, что в данном случае может привести к серьезным физиологическим нару-шениям. Действительно, вопреки распространенному мнению, дли-тельное пребывание человека в замкнутом пространстве приводит к удушью и гибели не из-за недостатка кислорода, а из-за избытка СО2.
Однако, присутствие в крови допустимых концентраций кислот, оснований или углекислого газа не вызывает нарушений кислотно-основного гомеостаза. Это означает, что в организме присутствуют системы, способные поддерживать концентрацию ионов водорода на заданном уровне. Таких систем в организме человека три: дыхатель-ная система (легкие), выделительная система (почки) и комплекс буферных систем.
Действительно, от кислотных оксидов (CO2) организм освобож-дается благодаря процессу дыхания, а нелетучие кислоты и основа-ния выводятся через почки с мочевыведением. Однако эти физиоло-гические процессы протекают медленно, быстрая же нейтрализация этих веществ и поддержание постоянства pH в норме осуществляется за счет физико-химических процессов, среди которых главная роль принадлежит протолитическим равновесиям в буферных системах биологических сред организма.
Типы буферных систем
Буферные системы (буферы) – это равновесные системы, способные поддерживать постоянство рН при разбавлении раствора или при добавлении к нему некоторого количества сильной кислоты или щелочи. Эта способность буферных систем называется буфер-ным действием. Растворы, содержащие одну или несколько буфер-ных систем называются буферными растворами. Интервал значений рН, в котором система проявляет буферные свойства, называется зоной буферного действия.
Буферные растворы применяются для сохранения активной реакции среды на определенном уровне, если тот или иной процесс (например, выращивание культуры бактерий, проведение фермента-тивной реакции и т.п.) должен быть проведен при постоянном значении рН.
Буферные системы могут быть двух типов. Некоторые примеры буферных систем и их характеристики приведены в таблице 1.
В биологических объектах буферные системы могут быть также образованы из ионов и молекул амфолитов, например, аминокислот-ные и белковые буферные системы.
В водных растворах a-аминокислоты присутствуют в виде равно-весной смеси биполярного иона, катионной и анионной форм:
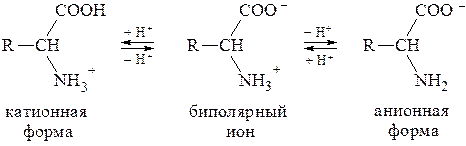
Таблица 1. Типы буферных систем.
| I. Слабая кислота и ее анион НА/А- | |||
| Название | Состав | Протолитическое равновесие | Зона буферного действия |
| Ацетатная | СН3СООН и CH3COONa | СН3СООН ⇄ CH3COO- + H+ | рН = 3,8 - 5,8 |
| Гидрокарбонатная | Н2СО3 и NaНСО3 | Н2СО3 ⇄ НСО3- + H+ | рН = 5,4 - 7,4 |
| Фосфатная | NaH2PO4 и Na2HPO4 | H2PO4– ⇄ HPO42- + H+ | рН = 6,2 - 8,2 |
| Гемоглобиновая | HHb и KHb | HHb ⇄ Hb- + H+ | рН = 7,2 - 9,2 |
| Оксигемоглобиновая | HHbO2 и KHbO2 | HHbO2 ⇄ HbO2- + H+ | рН = 6,0 - 8,0 |
| II. Слабое основание и его катион В/ВН+ | |||
| Аммонийная | NH3×H2O и NH4Cl | NH3 + H+ ⇄ NH4+ | рН = 8,2 - 10,2 |
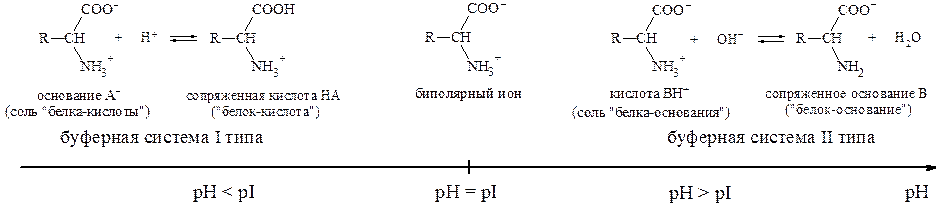 Рис.1. Буферные системы на основе амфолитов.
Рис.1. Буферные системы на основе амфолитов.
Соотношение между этими формами зависит от pH среды. В сильнокислых средах (pH = 1-2) преобладают катионные формы, в сильнощелочных (pH = 13-14) - анионные.
Полностью протонированная a-аминокислота (катионная форма), не содержащая ионогенных групп в радикале, с позиций теории Бренстеда является двухосновной кислотой, диссоциация которой описывается при помощи двух констант: 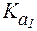 характеризует диссоци-ацию карбоксильной группы,
характеризует диссоци-ацию карбоксильной группы, 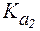 - протонированной аминогруппы.
- протонированной аминогруппы.
Значение pH, соответствующее наибольшей концентрации бипо-лярного иона, называется изоэлектрической точкой (pI). В общем случае величину pI вычисляют по формуле:
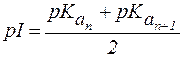 , ,
| (1) |
где n - максимальное число положительных зарядов в полностью протонированной форме.
Для аминокислот, не содержащих ионогенных групп в радикале, величину pI вычисляют по формуле:
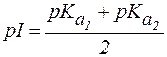
| (2) |
Пример 1. Рассчитать величину pI аргинина, если для этой a-аминокислоты: 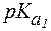 = 2,2;
= 2,2; 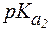 = 9,0;
= 9,0; 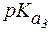 = 12,6.
= 12,6.
Решение.
Полностью протонированная форма аргинина выглядит так:
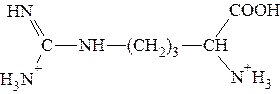
Видно, что n = 2. Поэтому:
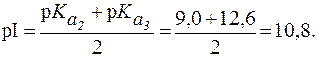
Растворы аминокислот с pH = pI не являются буферными. Они начинают проявлять буферное действие, когда к ним добавляют некоторое количество кислоты или щелочи. При этом образуется смесь двух форм белка - «белок-кислота» и «белок-основание» (рис.1). Из рис. 1. видно, что при pH < pI растворы белков и аминокислот могут проявлять свойства буферных систем I типа, а при pH > pI - II типа.
Механизм буферного действия
С точки зрения протолитической теории буферное действие растворов обусловлено наличием кислотно-основного равновесия общего типа:
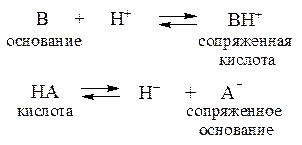
Сопряженные кислотно-основные пары А-/НА и В/ВН+ состав-ляют буферные системы.
Рассмотрим механизм буферного действия буферной системы на примере раствора, содержащего CH3COONa и СН3СООН. Уксусная кислота - слабый электролит, частично диссоциирующий на ионы:
СН3СООH ⇄ СН3СООН + H+
Ацетат натрия - сильный электролит, полностью распадающийся на ионы:
СН3СООNa  СН3СОО- + Na+
СН3СОО- + Na+
При добавлении сильной кислоты (например, НСl) сопряженное основание СН3СОО- связывает ионы Н+ в молекулы слабой кислоты:
СН3СОО- + H+  СН3СООН
СН3СООН
Таким образом, концентрация свободных ионов Н+ в растворе, а следовательно, и величина рН практически не изменяется.
Следует отметить, что при этом в буферной системе снижается концентрация анионов СН3СОО- и повышается концентрация моле-кул СН3СООН. В результате происходит небольшое изменение в соотношении концентраций слабой кислоты и ее соли и, как следст-вие, наблюдается незначительное изменение рН. Существенные отклонения значений pH (более чем на 1) наблюдаются в условиях практически полного (до 90%) расходования анионов СН3СОО-.
При добавлении сильной щелочи (например, КОН) усиливается диссоциация уксусной кислоты, поскольку выделяющиеся в раствор ионы Н+ реагируют с ионами ОН-, образуя воду:
СН3СООH + OH-  СН3СОО- + H2O
СН3СОО- + H2O
В этом случае также не происходит существенного изменения концентрации ионов Н+ в растворе, поскольку добавленные ионы ОН- оказываются связанными в молекулы слабого электролита - воды, но небольшое изменение в соотношении концентраций слабой кислоты и ее соли (уменьшение концентрации СН3СООН и увеличе-ние концентрации СН3СОО-) приводит к незначительному повыше-нию рН. Значительные отклонения значений pH (более чем на 1) наблюдаются в условиях практически полного (до 90%) расходования молекул кислоты.
Рассмотренные случаи показывают, что каждый компонент буферного раствора выполняет строго определенную функцию: за нейтрализацию добавленной кислоты «отвечают» анионы соли, а за нейтрализацию добавленной щелочи – молекулы кислоты.
Таким образом, для буферных растворов I типа справедливы заключения:
Чем больше концентрация соли, тем большее количество кис-лоты можно добавлять к буферу без существенного понижения рН.
Чем больше концентрация кислоты, тем большее количество щелочи можно добавлять к буферу без существенного повышения рН.
Механизм действия буферных систем II типа рассмотрим на примере раствора, содержащего аммиак и хлорид аммония.
В водном растворе гидратная форма аммиака проявляет свойства частично распадающегося на ионы слабого основания, тогда как хлорид аммония является сильным электролитом, полностью диссо-циирующим на ионы:
NH3∙H2O ⇄ NH4+ + OH-
NH4Сl  NH4+ + Cl-
NH4+ + Cl-
При добавлении сильной кислоты введенные в раствор ионы Н+ реагируют с ионами ОН-, образуя воду. При этом равновесие диссо-циации слабого основания смещается вправо, и в раствор переходит дополнительное количество ионов ОН-, компенсируя их затрату на реакцию. Поэтому значительного изменения рН не происходит, хотя из-за изменения соотношения между концентрациями основания и катиона наблюдается небольшое снижение рН.
При добавлении сильного основания равновесие диссоциации аммиака смещается влево, и добавленные в раствор ионы ОН- оказы-ваются связанными в молекулы присутствующими в растворе катионами NH4+, поэтому существенного отклонения рН не происхо-дит. Небольшое повышение рН связано с изменением соотношения между молекулами аммиака и катионами аммония в растворе.
Эти процессы описываются уравнениями:
NH3∙H2O + Н+  NH4+ + H2О;
NH4+ + H2О;
NH4+ + ОН- ⇄ NH3∙H2O,
из которых видно, что в буферной системе II типа каждый компонент также играет определенную роль: за нейтрализацию добавленной кислоты «отвечает» слабое основание, тогда как за нейтрализацию добавленной щелочи отвечает соль, создающая в растворе значитель-ную концентрацию катионов.
Таким образом, для буферных систем II типа можно заключить:
Чем больше концентрация слабого основания, тем большее коли-чество кислоты можно добавить к буферу без существенного снижения рН.
Чем больше концентрация соли, тем большее количество щелочи можно добавить к буферу без существенного повышения рН.
Значительное изменение рН буферного раствора произойдет только в том случае, когда большая часть одного или другого компо-нента раствора (более 90%) будет израсходована на связывание добавленных ионов в молекулы.
На основании приведенных примеров механизм буферного действия в общем случае можно определить следующим образом:
Буферное действие осуществляется за счет связывания добав-ляемых в раствор ионов Н+ или ОН- в малодиссоциированные соеди-нения в результате реакций этих ионов с соответствующими компонентами буферной системы.
Количественные характеристики буферных систем
Важн
| <== предыдущая страница | | | следующая страница ==> |
| ЗАНЯТИЕ №18 | | | РН буферных растворов |
Дата добавления: 2014-09-10; просмотров: 3706; Нарушение авторских прав

Мы поможем в написании ваших работ!