
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Приближенно сближение меридианов равно
g = Dl sinj,
где Dl = l-l0, причем l -долгота географического данной точки и l0 - долгота осевого меридиана; j - широта точки.
На рис. 3.4 показано соотношение между азимутами и дирекционными углами в пределах одной координатной зоны. Легко заметить, что для точек, расположенных к востоку от осевого меридиана зоны, сближение меридианов положительное, а к западу – отрицательное. При этом дирекционные углы в разных точках прямой линии равны a1 = a2 = a3. Поэтому обратный дирекционный угол в точке 3 отличается от прямого в точке 1 ровно на 180°, то есть a1-3 = a3-1 ± 180°. Азимуты же в разных точках прямой различаются: А1 ¹ А2 ¹ А3, что обусловлено различием сближения меридианов. Поэтому и А1-3 ¹ А3-1 ± 180°.
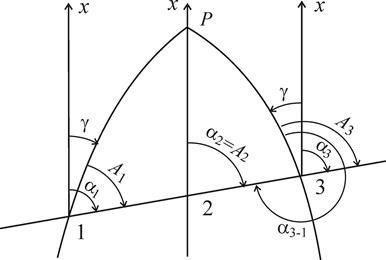
Рис. 3.4. Связь между азимутами и дирекционными углами: 1 – в западной половине зоны; 2 – на осевом меридиане; 3 – в восточной половине зоны; Р – полюс; 1Р, 3Р – меридианы; 2Р – осевой меридиан.
При использовании местной системы прямоугольных координат направление оси абсцисс x не связано с направлением осевого меридиана координатной зоны, и тогда дирекционные углы отсчитывают от положительного направления оси абсцисс х.
В практике вычислений находят применение также вспомогательные углы ориентирования – румбы. Румбом называют острый угол, измеряемый от ближайшего направления меридиана (северного или южного). Румбу приписывают название координатной четверти (СВ, ЮВ, ЮЗ, СЗ), в которой расположено заданное направление. Например, для a = 240°36¢ румб равен r = ЮЗ: 60°36¢.
3.2. Прямая и обратная геодезические задачи на плоскости
При вычислительной обработке выполненных на местности измерений, а также при проектировании инженерных сооружений и расчетах для перенесения проектов в натуру возникает необходимость решения прямой и обратной геодезических задач.
Прямая геодезическая задача. По известным координатам х1 и у1 точки 1, дирекционному углу a1-2 и расстоянию d1-2 до точки 2 требуется вычислить ее координаты х2, у2.
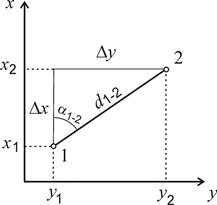
| Рис. 3.5. К решению прямой и обратной геодезических задач |
Координаты точки 2 вычисляют по формулам (рис. 3.5):
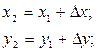 (3.4)
(3.4)
где Dх, Dу - приращения координат, равные
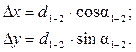 (3.5)
(3.5)
Обратная геодезическая задача. По известным координатам х1, у1 точки 1 и х2, у2 точки 2 требуется вычислить расстояние между ними d1-2 и дирекционный угол a1-2.
Из формул (3.5) и рис. 3.5 видно, что
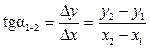 . (3.6)
. (3.6)
Для определения дирекционного угла a1-2 воспользуемся функцией арктангенса. При этом учтем, что компьютерные программы и микрокалькуляторы выдают главное значение арктангенса
w = 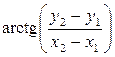 ,
,
лежащее в диапазоне -90°£w£+90°, тогда как искомый дирекционный угол a может иметь любое значение в диапазоне 0°£ a £ 360°.
Формула перехода от w к a зависит от координатной четверти, в которой расположено заданное направление или, другими словами, от знаков разностей Dy = y2 - y1 и Dx = х2 - х1(см. таблицу 3.1 и рис. 3.6).
Таблица 3.1
| I четверть | П четверть | Ш четверть | IV четверть | |
| Dх | + | - | - | + |
| Dу | + | + | - | - |
| w | + | - | + | - |
| Формулы | a=w | a=w+180° | a=w+180° | a=w+360° |
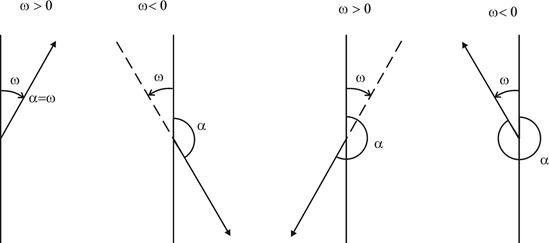
Рис. 3.6. Дирекционные углы и главные значения арктангенса в I, II, III и IV четвертях
Расстояние между точками вычисляют по формуле
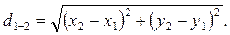 (3.6)
(3.6)
или другим путем – по формулам
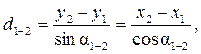
 (3.7)
(3.7)
Программами решения прямых и обратных геодезических задач снабжены, в частности, электронные тахеометры, что дает возможность непосредственно в ходе полевых измерений определять координаты наблюдаемых точек, вычислять углы и расстояния для разбивочных работ.
ПЛАН И КАРТА
4.1. План, карта, цифровая модель местности
Планом называется уменьшенное подобное изображение горизонтальной проекции небольшого участка местности.
Для составления плана местности расположенные на ней точки проецируют на уровенную поверхность по направлению отвесных линий. Ввиду малости участка отвесные линии оказываются практически параллельными, а фрагмент уровенной поверхности может рассматриваться как плоскость. Полученную проекцию местности уменьшают и изображают на плане. Степень уменьшения характеризуется масштабом плана.
Масштабом называется отношение длины отрезка на плане к длине горизонтальной проекции соответствующего отрезка местности. Масштаб записывают в виде дроби с числителем, равным единице, и знаменателем, показывающим, во сколько раз уменьшены на плане длины линий. При строительстве железных дорог для выбора варианта трассы используют планы масштабов 1:2000 и 1:5000, для рабочего проектирования - 1:1000 и 1:2000, для проектирования мостов, тоннелей, станций - 1:500 ¸ 1:2000.
Наряду с представлением масштаба в виде дроби (численного масштаба) пользуются именованным масштабом - его словесным описанием, например: “в одном сантиметре 20 метров”, что соответствует масштабу 1:2000.
Для измерения расстояний на плане, под его нижней рамкой, помещают линейный масштаб (рис. 4.1), на котором несколько раз отложено одно и то же расстояние, называемое основанием масштаба и равное обычно 2 см. Крайнее левое основание делят на более мелкие отрезки. Деления линейного масштаба оцифровывают в метрах.

Рис. 4.1 Линейный масштаб
Картой называют уменьшенное и обобщённое изображение на плоскости всей земной поверхности или значительных её частей. Для изготовления карты объекты местности проецируют на поверхность земного эллипсоида и полученное изображение переносят на плоскость. Такой перенос невозможно выполнить без искажений. Каковы будут искажения, определяется картографической проекцией – законом перехода от геодезических координат объектов к плоским координатам карты. В геодезии чаще всего пользуются равноугольными (или иначе - конформными) проекциями, сохраняющими без искажений углы и очертания малых объектов. Карты различаются также по виду изображения на них меридианов и параллелей. В конических проекциях параллели изображаются концентрическими окружностями, а меридианы – радиальными прямыми, углы между которыми пропорциональны разностям долгот. Если при этом углы между изображениями меридианов равны разностям долгот, проекция называется азимутальной. В цилиндрических проекциях линии меридианов и параллелей изображаются взаимно перпендикулярными прямыми.
Топографические карты в России издают в поперечной цилиндрической проекции Гаусса - равноугольной проекции, в которой прямыми линиями без искажений изображаются осевой меридиан зоны и экватор.
В условиях применения компьютерных технологий, наряду с изображениями местности на бумажных носителях - картами и планами, используются их цифровые аналоги.
Цифровой моделью местности (ЦММ) называется представленное в виде цифровых кодов и хранимое на магнитных носителях логико-математическое описание местности, адекватное по содержанию плану местности. Основным содержанием ЦММ является топографическая информация: координатыи высоты точек, очертания объектов, их свойства. ЦММ содержит и общую информацию - название участка, систему координат и высот и др.
Цифровой картой называют цифровую модель значительного участка земной поверхности, сформированную с учётом генерализации изображаемых объектов и принятой картографической проекции.
Электронной картой называется изображение местности на экране дисплея, полученное на основе цифровой карты.
4.2. Разграфка и номенклатура топографических карт и планов
Топографические карты издают на листах со сторонами 40–50 см. В основу разграфки (нарезки) карт положена карта масштаба 1:1000000. Она издается на листах размерами 4° по широте и 6° по долготе. Множество листов такой карты по направлению параллелей образует ряды шириной по 4°, а по направлению меридианов - колонны шириной по 6°.
Таблица 4.1
| Обозначе-ние ряда | Границы ряда по широте | Обозначе-ние ряда | Границы ряда по широте | Обозначе-ние ряда | Границы ряда по широте |
| A | 0° - 4° | I | 32° - 36° | Q | 64° - 68° |
| B | 4 – 8 | J | 36 – 40 | R | 68 – 72 |
| C | 8 – 12 | K | 40 – 44 | S | 72 – 76 |
| D | 12 – 16 | L | 44 – 48 | T | 76 – 80 |
| E | 16 – 20 | M | 48 – 52 | U | 80 – 84 |
| F | 20 – 24 | N | 52 – 56 | Y | 84 – 88 |
| G | 24 – 28 | O | 56 – 60 | Z | 88 – 90 |
| H | 16 – 20 | P | 60 – 64 |
Ряды обозначают заглавными буквами латинского алфавита A, B, C, D, ..., начиная от экватора по направлениям к северу и югу (табл. 4.1). Колонны нумеруют арабскими цифрами 1, 2, ... , 60, начиная от меридиана 180° в направлении с запада на восток. Каждому листу карты масштаба 1:1000000 присвоен номенклатурный номер, состоящий из буквы соответствующего ряда и номера колонны, например, M-42.
Для карт масштаба 1:500000 лист масштаба 1:1000000 меридианом и параллелью делят на 4 листа, обозначая их прописными буквами А, Б, В, Г. Номенклатурные номера листов карты образуют добавлением соответствующей буквы к номенклатурному номеру листа масштаба 1:1000000 (например, M-42-Г).
Для карт масштаба 1:200000 лист масштаба 1:1000000 делят на 36 листов, нумеруя их римскими цифрами I, II, ... , XXXVI.
Для карт масштаба 1:100000, разделив лист масштаба 1:1000000 по широте и долготе на 12 частей, получают границы 144 листов (рис. 4.2, а), которые нумеруют цифрами 1, 2, ... , 144. Номенклатура каждого листа складывается из номенклатуры листа масштаба 1:1000000 и номера листа. На рисунке выделен лист M-37-87.
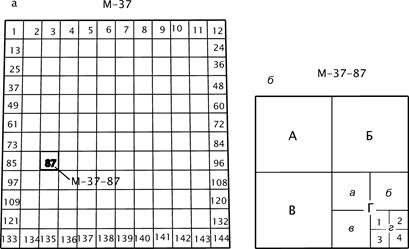
Рис. 4.2. Разграфка листов карт масштабов: а – 1:100000; б – 1:50000, 1:25000, 1:10000.
Разграфка карт масштабов 1:50000, 1:25000 и 1:10000 формируется делением на четыре части листа более мелкого масштаба (соответственно - 1:100000, 1:50000, 1:25000) и добавлением к номенклатуре предыдущего масштаба соответствующего знака, как показано на рис. 4.2, б и в табл. 4.2.
Таблица 4.2
| Номенклатура | Число листов | Размеры листа | ||
| Масштаб | (последнего листа карты) | карты | По Широте | по долготе |
| 1:1000000 1:100000 1:50000 1:25000 1:10000 | M-37 M-37-144 M-37-144-Г M-37-144-Г-г M-37-144-Г-г-4 | - 12´12=144 2´2=4 2´2=4 2´2=4 | 4° 20¢ 10¢ 5¢ 2¢30² | 6° 30¢ 15¢ 7¢30² 3¢45² |
Для планов масштабов 1:5000 и 1:2000 применяется два вида разграфки - трапециевидная, в которой рамками планов служат параллели и меридианы, и прямоугольная, в которой рамки совмещают с линиями сетки прямоугольных координат.
При трапециевидной разграфке границы листов планов масштаба 1:5000 получают делением листа масштаба 1:100000 на 256 частей (16´16), которые нумеруют от 1 до 256. Номенклатура, например листа №70, записывается так M-37-87(70).
Разграфку листов масштаба 1:2000 получают делением листа масштаба 1:5000 на 9 частей (3´3) и обозначают добавлением буквы русского алфавита, например, M-37-87(70-и).
Прямоугольная разграфка применяется для планов населённых пунктов и для участков площадью менее 20 км2, а также для планов масштабов 1:1000 и 1:500.
При съёмке отдельного участка план может быть составлен и на листе нестандартного формата.
4.3. Условные знаки топографических карт и планов
Рамки карты и координатные линии.Листы топографических карт имеют три рамки: внутреннюю, минутную и внешнюю. Внутреннюю рамку образуют отрезки параллелей, ограничивающих площадь карты с севера и юга, и отрезки меридианов, ограничивающих её с запада и востока. Значения широт и долгот на линиях внутренней рамки связаны с номенклатурой карты и написаны в каждом её углу.
Между внутренней и внешней рамками помещена минутная рамка, на которой нанесены деления, соответствующие одной минуте широты (слева и справа) и долготы (наверху и внизу). Точками на рамке отмечены десятки секунд.
Система прямоугольных координат на карте представлена километровой сеткой, образованной проведенными через 1 км координатными линиями x и y. Значения x и y, выраженные в километрах, надписаны на выходах линий за внутреннюю рамку карты.
Планы масштабов 1:5000-1:500 с прямоугольной разграфкой имеют только сетку прямоугольных координат. Ее линии проведены через 10 см.
Условные знаки.На планах и картах объекты местности изображают условными знаками.
Условные знаки различают контурные, внемасштабные и линейные.
Контурными условными знаками изображают объекты, форма и размеры которых могут быть переданы в масштабе плана (карты). К ним относятся земельные угодья (леса, сады, пашни, луга), водоёмы, а для более крупных масштабов - здания, сооружения. Очертания объектов (контуры) на плане показывают точечным пунктиром или линиями определённой толщины и цвета. Внутри контура помещают знаки, указывающие характер объекта.
Внемасштабными условными знаками изображают объекты, которые необходимо нанести на план, но невозможно изобразить в масштабе (бензоколонки, колодцы, пункты геодезической сети и др.).
Линейными условными знаками изображают объекты, длина которых выражается в масштабе плана, а ширина не выражается (линии электропередач и связи, трубопроводы, ограды, тропы).
Для отражения характеристик изображаемых объектов многие условные знаки сопровождаются пояснительными подписями. Так, при изображении железной дороги указывают высоту насыпи и глубину выемки, ширину колеи на узкоколейной дороге. При изображении шоссе указывают его ширину и материал покрытия; при изображении линий связи – число проводов и их назначение; при изображении лесов – породу деревьев, среднюю высоту, толщину стволов и расстояние между деревьями.
Изображение рельефа.На картах и планах рельеф изображают с помощью горизонталей, высотных отметок и условных знаков.
Горизонтали - линии сечения земной поверхности равноотстоящими уровенными поверхностями. Иными словами, горизонтали - это линии равных высот. Горизонтали, подобно другим точкам местности, проецируют на уровенную поверхность Q и наносят на план (рис. 4.3).
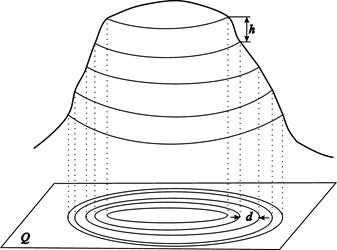
Рис. 4.3. Горизонтали: h – высота сечения рельефа; d – заложение
Разность h высот смежных горизонталей, равная расстоянию между секущими поверхностями, называется высотой сечения рельефа. Значение высоты сечения подписывают у нижней рамки плана.
Горизонтальное расстояние между соседними горизонталями называется заложением. Минимальным в данном месте является заложение, перпендикулярное к горизонталям, – заложение ската. Чем меньше заложение ската, тем круче скат.
Направление ската указывают бергштрихами - короткими штрихами у некоторых горизонталей, направленными в сторону спуска. На отдельных горизонталях в их разрывах пишут их высоту так, чтобы верх цифр указывал в сторону подъёма.
Горизонтали с круглыми значениями высот делают утолщёнными, а для отражения деталей рельефа используют полугоризонтали – штриховые линии, соответствующие половине высоты сечения рельефа, а также вспомогательные горизонтали с короткими штрихами, проводимые на произвольной высоте.
Изображение рельефа горизонталями дополняется вписыванием на план отметок высот около характерных точек рельефа и специальными условными знаками, изображающими обрывы, скалы, овраги и т. п.
Основными формами рельефа являются гора, котловина, хребет, лощина и седловина (рис. 4.4).
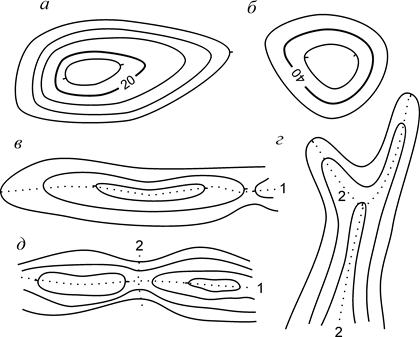
Рис. 4.4. Основные формы рельефа: а – гора; б – котловина; в – хребет; г – лощина; д – седловина; 1 – водораздельная линия; 2 – водосливная линия.
Гора (возвышенность, холм, курган, сопка) изображается замкнутыми горизонталями с бергштрихами, обращёнными наружу (рис. 4.4, а). Характерными точками горы являются её вершина и точки у подошвы.
Котловина (впадина) тоже изображается замкнутыми горизонталями, но с бергштрихами, обращёнными внутрь (рис. 4.4, б). Характерными точками котловины являются точки на её дне и вдоль бровки.
Хребет - вытянутая возвышенность. Изображается огибающими гребень хребта и идущими по его скатам вытянутыми горизонталями (рис. 4.4, в). Бергштрихи, как и у горы, обращены наружу. Характерной линией хребта является проходящая вдоль его гребня водораздельная линия.
Лощина (долина, ущелье, овраг, балка) – вытянутое в одном направлении углубление. Изображается вытянутыми, горизонталями с бергшрихами, обращёнными внутрь (рис. 4.4, г). Характерной линией лощины является водосливная линия (тальвег) - линия, по которой сбегает вода.
Седловина (перевал) – понижение между двумя возвышенностями (рис. 4.4, д). По обе стороны к седловине примыкают лощины. Седловина – это место пересечения водораздельной и водосливной линий.
4.4. Решение задач по топографической карте
Измерение расстояний на картах и планах.Для измерения расстояния на карте его берут на циркуль-измеритель и переносят на помещённый под южной рамкой карты линейный масштаб.
Более точно расстояние измеряют линейкой с миллиметровыми делениями. Отсчёт по линейке, выраженный в сантиметрах, умножают на число метров, указанное в именованном масштабе карты.

| Рис. 4.5. Поперечный масштаб |
Ещё точнее измерения выполняются с применением поперечного масштаба (рис. 4.5.). На металлической линеечке через m интервалов выгравированы параллельные линии – горизонтали (обычно m = 10). К ним восставлены перпендикуляры – вертикали, расстояние между которыми называют основанием масштаба d (обычно d = 2 см). Крайнее левое основание разделено на n частей и через полученные точки проведено n наклонных линий – трансверсалей (обычно n =10 или 5). Длины отрезков, параллельных основанию, на поперечном масштабе равны: между соседними вертикалями – d, между соседними трансверсалями – d/n. Длины отрезков между вертикалью и исходящей из той же точки трансверсалью изменяются в пределах от 0 до d/n. Наименьшее деление поперечного масштаба, определяющее его точность, равно d/(mn).
Для удобства пользования поперечным масштабом деления основания и горизонтали оцифровывают в соответствии с масштабом плана. Оцифровка на рисунке соответствует масштабу 1:500.
Для измерения расстояния берут его в раствор циркуля-измерителя. Правую его ножку ставят на одну из вертикалей поперечного масштаба, а левую – на одну из трансверсалей, но так, чтобы обе ножки оказались на одной и той же горизонтали. Измеренное расстояние равно сумме расстояний, соответствующих числу охваченных раствором циркуля целых оснований, десятых долей основания и сотых, оцениваемых по положению ножки циркуля на трансверсали. На рисунке отрезок ab имеет длину 20+3+0,7=23,7 м. Длина отрезка cd равна 30+5+0,45=35,45 м. Из второго примера видно, что длину отрезка удаётся измерить с точностью половины наименьшего деления (в данном случае 0,05 м).
Для измерения длин извилистых линий служит специальный прибор - курвиметр, снабжённый колёсиком, которое прокатывают вдоль измеряемой линии. Вращение передаётся на стрелку циферблата, по которому прочитывают измеренное расстояние.
Определение координат точек.Для определения географических координат служит минутная рамка карты. Через круглые значения минут широты на западной и восточной рамках южнее определяемой точки прочерчивают линию. На рис. 4.6, а показан отрезок такой линии с широтой 57°20¢. Взяв на циркуль-измеритель расстояние а от определяемой точки M до прочерченной линии, откладывают его на рамке карты и, по десятисекундным делениям соображают число секунд. На рисунке широта точки M равна 57°20¢32".
Для определения долготы через одинаковые значения минут на северной и южной рамках прочерчивают вертикальную линию. Расстояние от точки до линии переносят измерителем на северную или южную рамку и соображают число секунд.
Прямоугольные координаты определяют, пользуясь километровой сеткой, линии которой параллельны координатным осям x и y. Координаты точки P (рис. 4.6, б) определяются по формуле
xP = xю + Dx, yP = yз + Dy,
где xюи yз- значения координат на линиях сетки, проходящих южнее и западнее точки Р. Они подписаны (в километрах) на выходах линий за рамку. Отрезки Dx и Dy измеряют.
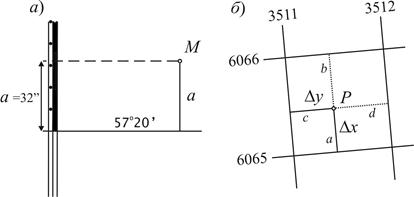
Рис. 4.6. Определение координат точек: а - географических; б – прямоугольных.
Повысить точность определения координат точки Р можно, измерив расстояния a и b до ближайших южной и северной линий сетки, а также расстояния c и d до ближайших западной и восточной линий сетки. Отрезки Dx и Dy, выраженные в метрах, вычисляют по формулам
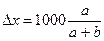 ,
, 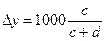 , (4.1)
, (4.1)
где множитель 1000 - длина стороны квадрата километровой сетки в метрах.
Дополнительный эффект измерения отрезков a, b, c, d и использования формул (4.1) состоит в ослаблении погрешностей, вызванных деформацией бумаги. Такой же прием может быть применен и при определении географических координат.
Определение углов ориентирования. Дирекционный угол направления отрезка на карте измеряют транспортиром как угол, отсчитываемый по направлению часовой стрелки от северного направления линии километровой сетки до направления отрезка. При необходимости перед измерением отрезок удлиняют до пересечения с линией сетки.
Для определения азимута А направления сначала измеряют его дирекционный угол a. Затем вычисляют азимут: А=a+g, где g - сближение меридианов, значение которого подписано под южной рамкой карты и показано на помещённой там же схеме.
Можно азимут измерить и непосредственно. Через одноименные значения минут долготы проводят вертикальную линию - меридиан. Угол между северным направлением меридиана и направлением отрезка и есть азимут.
Под южной рамкой карты и на схеме указано также склонение магнитной стрелки d, позволяющее вычислить магнитный азимут направления по формуле Ам= А-d.
Определение высот точек. Высота точки, лежащей на горизонтали, равна высоте горизонтали. Высоты отдельных горизонталей подписаны в их разрыве. Высоты других горизонталей легко сообразить, зная высоту сечения рельефа, а также высоты подписанных горизонталей и высоты тех характерных точек рельефа, у которых подписаны их отметки. При этом учитывают, что высоты горизонталей кратны высоте сечения рельефа.
Высота точки M, расположенной между двумя горизонталями (рис. 4.7) определяется по формуле
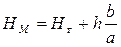 ,
,
где Hг - высота меньшей горизонтали, h – высота сечения рельефа, а отрезки a и b – заложение ската и расстояние от точки до горизонтали, измеряемые по карте линеечкой.
Построение профиля. Для построения профиля по линии, проведенной на карте, определяют высоты точек в местах её пересечения с горизонталями, водораздельными и водосливными линиями. Измеряют горизонтальные расстояния до них от начальной точки линии. При построении профиля по горизонтальной оси откладывают расстояния, а по вертикальной - высоты. Для наглядности вертикальный масштаб принимают крупнее горизонтального (в 10, а то и в 50 раз).
Определение уклонов и углов наклона. Отрезки линий на земной поверхности обычно имеют наклон, отчего начало и конец отрезка находятся на разных высотах. Разность их высот – превышение, а проекция отрезка на горизонтальную плоскость – его горизонтальное проложение.
Уклоном i линии называется отношение превышения h к горизонтальному проложению d:
i = h / d. (4.2)
Для определения по карте уклона линии на участке KL между двумя горизонталями (рис. 4.7) измеряют его горизонтальное проложение – заложение d. Поскольку концы отрезка лежат на смежных горизонталях, превышение h между ними равно высоте сечения рельефа, подписанному под южной рамкой карты. Воспользовавшись формулой (4.2), вычисляют уклон, который принято выражать в тысячных. Если, например, h=1 м, d=48 м , то уклон равен i =1 м / 48 м = 0,021=21‰.
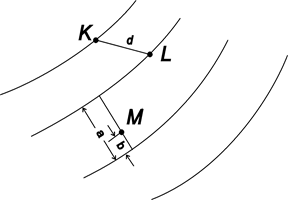
| Рис. 4.7. Определение высоты точки M и уклона на отрезке KL |
С другой стороны, отношение превышения h к горизонтальному проложению d равно тангенсу угла n наклона линии. Поэтому
i = tg n,
что позволяет, вычислив уклон определить по нему угол наклона.
При пользовании картой углы наклона не вычисляют, а определяют с помощью графика заложений (рис. 4.8), расположенного под южной рамкой карты. По горизонтальной оси графика отложены углы наклона, а по вертикальной - соответствующие этим углам заложения d, выраженные в масштабе карты и рассчитанные по формуле
d = h ¤(M tg n),
где h - высота сечения рельефа, а M – знаменатель масштаба карты.
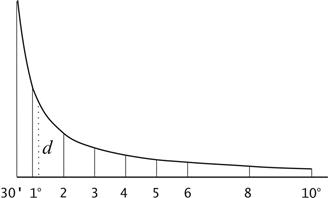
| Рис. 4.8. График заложений |
Для определения угла наклона отрезка KL (рис. 4.7), расположенного между горизонталями, берут его в раствор циркуля и на графике заложений (рис. 4.8) находят такой угол, над которым ордината равна раствору циркуля d. Это и есть искомый угол наклона.
При необходимости многократного определения уклонов пользуются графиком уклонов, построенным аналогично графику заложений, но с отложением по горизонтальной оси не углов наклона, а уклонов.
Проведение линии с уклоном, не превышающим заданного предельного. Необходимость решения такой задачи возникает, например, при выборе трассы для будущей дороги. Вычисляют соответствующее заданному предельному уклону iпр заложение, выраженное в масштабе карты, 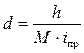 (здесь M – знаменатель масштаба). .
(здесь M – знаменатель масштаба). .
| 
|
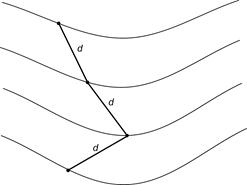
| Рис. 4.9. Построение линии с заданным уклоном | Рис. 4.10. Водосборная площадь |
Чтобы уклон линии не превосходил iпр, ни одно заложение на ней не должно быть меньше, чем рассчитанное d. Если расстояние между горизонталями больше рассчитанного, направление линии можно выбирать произвольно. В противном случае в раствор циркуля берут отрезок, равный d, и строят ломаную линию, умещая между горизонталями рассчитанное предельное заложение (рис. 4.9).
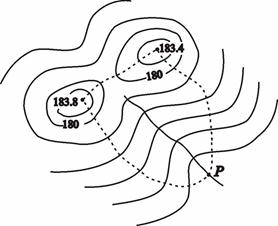
Определениеграницводосборной площади (бассейна). Водосборной называют площадь, с которой дождевые и талые воды поступают в данное русло. Определение водосборной площади необходимо, например, при проектировании дороги для расчёта отверстия моста или трубы.
Для определения границ водосборной площади на карте проводят водораздельные линии, а затем от проектируемого сооружения к водораздельным линиям проводят линии наибольшего ската, перпендикулярные горизонталям.
Например, водосборная площадь, для точки Р, где предстоит строительство трубы, (рис. 4.10), ограничена штриховой линией, образованной водораздельной и двумя линиями наибольшего ската.
4.5. Определение площадей по картам и планам
Аналитический способ. Если участок представляет собой замкнутый многоугольник, то, сняв с плана прямоугольные координаты его вершин, площадь участка вычисляют по формуле:
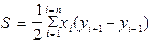
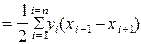 ,
,
где i - номера вершин многоугольника, пронумерованных по ходу часовой стрелки.
По этой же формуле можно вычислить площадь с криволинейными границами, если координаты точек границы сняты так часто, что отрезки между точками можно считать прямыми. В последнем случае съём координат выполняют с помощью специального прибора – дигитайзера, а вычисления выполняют на ЭВМ.
Графические способы.Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют.
Разбиение площади на простые фигуры выполняют также, применяя палетки. Палетка - лист прозрачного материала (восковки, лавсана, пластика), на который нанесена сетка квадратов размером 2×2 мм или система равноотстоящих параллельных линий. Наложив палетку с квадратами на план, подсчитывают число квадратов, уместившихся в измеряемой площади, оценивая дробные части квадратов на краях участка на глаз. Результат подсчёта умножают на площадь одного квадрата.
Палеткой с параллельными линиями площадь делится на трапеции, в каждой из которых измеряют длину средней линии. Суммируя площади трапеций, равные произведению длины средней линии на расстояние между линиями, определяют площадь участка.
Точность определения площади с помощью палеток - 1/50.
Полярный планиметр. Планиметрами называются приборы для измерения площадей. Наиболее распространён полярный планиметр (рис. 4.11). Он состоит из двух рычагов – полюсного 1 и обводного 4, соединяемых шарниром 8. Полюс планиметра (массивный цилиндр 2 с иглой, втыкаемой в бумагу) в процессе измерения площади остается неподвижным. На конце длинного плеча обводного рычага укреплен шпиль 3 (или лупа с маркой в виде креста в ее центре), которым обводят контур измеряемой площади. На коротком плече обводного рычага крепится каретка с мерным колесиком 6, опирающимся на поверхность бумаги, и счетным механизмом. Когда обводной шпиль 3 (или марка) перемещается по линии контура перпендикулярно рычагу, мерное колесико 6 катится по бумаге. При перемещении обводного шпиля по направлению рычага колесико скользит по бумаге, не вращаясь. При перемещении шпиля в иных направлениях происходит и вращение, и скольжение. Суммарное число оборотов колесика, накопленное при обводке шпилем контура, пропорционально площади, ограниченной контуром.

Рис. 4.11. Полярный планиметр
Для подсчета числа оборотов вращение колесика передается на циферблат5. По ободу колесика нанесено 100 делений. Отсчеты по шкале обода берут с помощью верньера 7. Отсчет по планиметру (рис. 4.12) состоит из отсчета числа целых оборотов колесика по циферблату (на рисунке – цифра 6), отсчета десятых и сотых долей оборота - по шкале обода против нуля верньера (цифры 4 и 2) и тысячных долей оборота – по номеру штриха верньера, совпадающего со штрихом на шкале обода (цифра 2).
Для измерения площади, обводят её контур, делая при этом два отсчёта по планиметру: один n1- до обвода, другой n2- после. Площадь вычисляют по формуле
S = c·(n2- n1) , (4.3)
где c – цена деления планиметра. Для надёжности площадь измеряют 3 - 5 раз и полученные результаты осредняют.
Если во время измерений полюс планиметра располагался внутри измеряемой площади, то вместо формулы (4.3) используют формулу
S = c·(n2- n1+ Q) ,
где Q - постоянная планиметра.
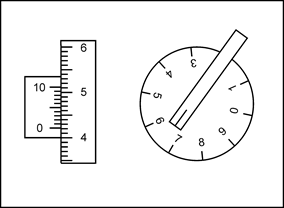
Рис. 4.12. Отсчет по планиметру: 6422.
Цена деления планиметра c зависит от длины обводного рычага и регулируется перемещением по нему каретки с мерным колёсиком и счётным механизмом. Перед измерением площади цену деления планиметра определяют. При этом, расположив полюс в стороне, обводят фигуру, площадь S0которой известна (например, квадрат километровой сетки на карте) и вычисляют цену деления
с = S0/(n2- n1).
Для определения постоянной Q обводят фигуру с известной площадью, поместив полюс внутри этой площади, после чего вычисляют
Q = (S0 /c) - (n2- n1).
Точность определения площади планиметром - 1/300.
Электронные планиметры. Электронный полярный планиметр устроен подобно механическому, но имеет электронное счетное устройство и жидкокристаллический дисплей.
Электронный роликовый планиметр катится на двух высокофрикционных абразивных роликах, измеряющих смещения по направлению качения. Поворотная штанга с курсором, перемещаемым по контуру площади, измеряет смещения в поперечном направлении. Счетное устройство вычисляет площадь и высвечивает ее величину на дисплее.
Электронный роликовый планиметр-дигитайзер позволяет, кроме измерения площади, снимать координаты точек и решать некоторые задачи – определение радиуса окружности, длины дуги, площади сегмента и др. Возможна связь с компьютером через стандартный интерфейс.
| <== предыдущая страница | | | следующая страница ==> |
| ОРИЕНТИРОВАНИЕ ЛИНИЙ. ПРЯМАЯ И ОБРАТНАЯ ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИ НА ПЛОСКОСТИ | | | МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ |
Дата добавления: 2014-09-10; просмотров: 576; Нарушение авторских прав

Мы поможем в написании ваших работ!