МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ

5.1 Погрешности измерений

Геодезические работы связаны с выполнением измерений различных величин - расстояний, превышений, углов и др. Измерения могут выполняться непосредственным сравнением измеряемой величины с единицей меры – прямые измерения, и посредством ее вычисления как функции других непосредственно измеренных величин – косвенные измерения.

Результаты измерений всегда содержат некоторые погрешности. Погрешностью Δ называют отклонение результата измерения l от истинного значения измеряемой величины Х.

Δ = l – Х (5.1)

Погрешности проявляются, например, при многократном измерении одной и той же величины – получаемые результаты всегда несколько различаются между собой, и значит, неизбежно отличаются от истинного значения, т.е. содержат погрешности.

Причинами, порождающими погрешности результатов измерений, являются несовершенство измерительных приборов, несовершенство органов чувств наблюдателя, внешние условия, влияющие на измерения.

Измерения, выполненные однотипными приборами, одинаковыми методами и в одинаковых условиях, принято считать равноточными, а выполненные разными приборами и методами, в разных условиях считают неравноточными.

Различают три основных вида погрешностей: случайные, систематические и грубые.

Грубые погрешности – необычно большие погрешности, вызванные небрежностью наблюдателя, неисправностью прибора или резким отклонением от нормы условий измерений. Грубые погрешности выявляют путем выполнения и анализа избыточных измерений. Результаты измерений, содержащие грубые погрешности, отбрасывают, бракуют.

Систематические погрешности – такие, которые при повторных измерениях остаются постоянными, или изменяются закономерным образом.

Причины и закономерности появления систематических погрешностей должны быть изучены, и сами погрешности исключены из результатов измерений путем введения соответствующих поправок, применением надлежащих методик измерений, юстировкой приборов.

Случайные погрешности – такие, которые при повторных измерениях изменяются случайным образом. Ни знак, ни значение случайной погрешности предвидеть невозможно. Поэтому невозможно исключить случайные погрешности из результатов измерений. Можно лишь при обработке измерений ослабить их влияние. Пути к такому ослаблению указывает теория погрешностей измерений.

В дальнейшем будем полагать, что результаты измерений свободны от грубых и систематических и содержат только случайные погрешности.

5.2 Свойства случайных погрешностей

Теоретические исследования и опыт измерений показывают, что случайные погрешности обладают следующими основными свойствами:

- при определенных условиях измерений, случайные погрешности по абсолютной величине не могут превышать известного предела;

- малые по абсолютной величине погрешности появляются чаще, чем большие.

- положительные погрешности встречаются так же часто, как и отрицательные;

- среднее арифметическое из всех случайных погрешностей равноточных измерений одной и той же величины при неограниченном возрастании числа измерений n стремится к нулю, т.е.

, (5.2)

где [ ] – обозначение суммы.

Формула (5.2) выражает свойство компенсации случайных погрешностей. Этим свойством обладает и сумма попарных произведений случайных погрешностей

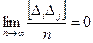, (i, j = 1, 2, 3 ... n; i ¹ j). (5.3)

5.3 Характеристики точности измерений

Каждая погрешность в отдельности не может характеризовать точность измерений, поскольку она случайна. Нужна такая оценка, которая характеризует точность в среднем.

Общепринятой характеристикой точности является предложенная К.Ф. Гауссом средняя квадратическая погрешность

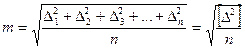, (5.4)

где Δ₁, Δ₂, …, Δ_n – случайные погрешности измерений. Достоинством этой характеристики является ее устойчивость, независимость от знаков отдельных погрешностей и усиленное влияние больших погрешностей.

Теоретически строгим значением средней квадратической погрешности считают оценку, получаемую по формуле (5.4) при бесконечно большом числе измерений, то есть при n®¥. Такую строгое значение средней квадратической погрешности часто именуют термином стандарт.

На практике приходится пользоваться ограниченным числом измерений, отчего оценки, вычисленные по формуле (5.4) вследствие случайного характера погрешностей Δ_i отличаются от строгой оценки – стандарта. Средняя квадратическая погрешность определения m по формуле (5.4) приближенно равна .

Формула (5.4) находит применение при исследовании точности геодезических приборов и методов измерений, когда известно достаточно точное, близкое к истинному, значение X измеряемой величины. Но обычно значение измеряемой величины заранее неизвестно. Тогда вместо формулы Гаусса пользуются формулой Бесселя (см. раздел 5.5), определяющей среднюю квадратическую погрешность по отклонениям результатов измерений от среднего.

В большинстве случаев погрешности измерений распределены по нормальному закону, установленному Гауссом. Это означает, что в интервал от –m до + m попадает 68,27% результатов повторных измерений одной и той же величины. В интервал от –2 m до +2 m попадает 95,45%, а в интервал от –3 m до +3 m попадает 99,73%.

Таким образом, вероятность того, что случайная погрешность превышает 2 m, равна 4,5%, а что она превышает 3 m - лишь 0,27%. Поэтому погрешности, большие 2 m, считают практически невероятными и относят к числу грубых погрешностей, промахов.

Величину 2 m называют предельной погрешностью и используют как допуск при отбраковке некачественных результатов измерений.

D_пред = 2 m.

В ряде случаев за предельно допустимую погрешность принимают величину 3 m.

Величины D, m, D_пред, выражаемые в единицах измеряемой величины, называются абсолютными погрешностями.

Наряду с абсолютными применяются также и относительные погрешности, представляющие собой отношение абсолютной погрешности к измеряемой величине. Относительную погрешность принято выражать в виде простой дроби с единицей в числителе, например

,

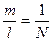где l -­ значение измеряемой величины, а N – знаменатель дроби.

Относительные погрешности используют, например, когда точность результата измерения зависит от измеряемой величины. Так при одинаковой абсолютной погрешности двух измеренных линий точнее измерена та, длина которой больше.

5.4 Средняя квадратическая погрешность функции измеренных величин.

В практике геодезических измерений определяемые величины обычно являются функциями других, непосредственно измеряемых величин. Рассмотрим функцию u независимых переменных x, y, z, …

u = f (x,y,z…). (5.5)

Продифференцируем функцию (5.5) по всем переменным и заменим дифференциалы du, dx, dy, dz, …. погрешностями Du, Dx,Dy,Dz, ….

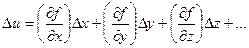
Получили выражение случайной погрешности Du в зависимости от случайной комбинации погрешностей Dx,Dy,Dz, …. Положим, что имеем n таких комбинаций, которым соответствует n выражений:

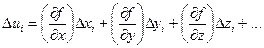(i = 1, 2, …, n)

Возведем полученные выражения в квадрат, сложим и разделим на n:

,

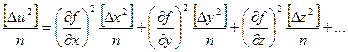
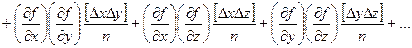где квадратными скобками обозначены суммы.

Устремим число комбинаций в бесконечность (n ® ¥) и, воспользовавшись выражениями (5.4) и (5.3), получим: 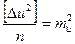, , 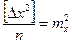, , 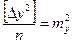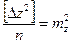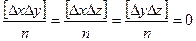. И окончательно

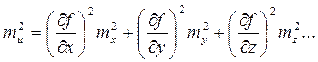(5.6)

Итак, квадрат средней квадратической погрешности функции общего вида равен сумме квадратов произведений частных производных по каждой переменной, умноженных на их средние квадратические погрешности.

Частные случаи.

1. Функция u является суммой переменных x , y, z:

u = x + y + z.

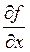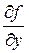В этом случае =1, =1, 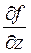=1. Следовательно

= + + .

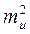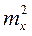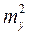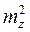2. Функция u является разностью переменных x и y:

u = x - y.

В этом случае 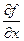=1, 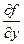=-1. Следовательно

= + .

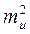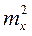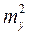3. Функция u имеет вид:

u = k× x,

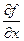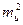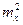где k – постоянный множитель. Теперь = k, поэтому = k²× и

m_u = k× m_x.

4. Функция u является линейной функцией от x, y, z, …:

u = k₁ x + k₂ y + k₃ z …,

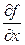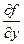где k_i ­постоянные множители. Теперь частные производные равны =k₁, = k₂, 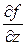= k₃. Поэтому

.

Рассмотрим примеры.

Пример 1. Определить среднюю квадратическую погрешность превышения, вычисленного по горизонтальному расстоянию d=124,16 м и углу наклона n=2°16´, если m_d = 0,06 м, а m_n = 1´.

Превышение вычисляют по формуле

h = d tgν.

Продифференцируем формулу по переменным d и n:

, .

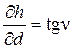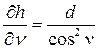Используя формулу общего вида (5.6) получим

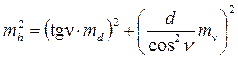
Подставляя исходные данные, найдем

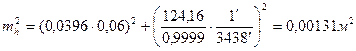
где 3438¢ -­ число минут в радиане. И окончательно m_h=0,036 .м.

Пример 2. При геометрическом нивелировании (см. раздел 9.2) превышение вычисляют как разность отчетов по рейкам

h = a - b.

Отчеты берут с точностью m_a = m_b = 2 мм. Находим среднюю квадратическую погрешность превышения

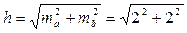= 2,8 мм

Пример 3. Выведем формулу допустимой угловой невязки замкнутого теодолитного хода (см. раздел 9.4). Невязку вычисляют по формуле

f_b= b₁+ b₂+ ¼+ b_n-180°(n-2),

где b_i – измеренные углы (i = 1, 2, ¼, n) и n – их число.

Невязка - результат погрешностей в углах b_i. Поэтому средняя квадратическая погрешность невязки равна

m_f = = ,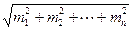

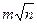где m₁ = m₂ =¼ = m_n = m – средняя квадратическая погрешность измерения угла. Примем ее равной m = 0,5¢.

Допуском угловой невязки (f_b)_доп служит предельная погрешность (f_b)_пред=2m_f. Получаем формулу

(f_b)_доп = 1¢ .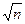

5.5 Математическая обработка результатов прямых равноточных измерений

Арифметическая средина результатов равноточных измерений. Пусть имеем результаты многократных равноточных измерений одной величины: l₁, l₂, …, l_n. Рассмотрим их среднее арифметическое

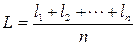. (5.7)

Из (5.1) следует l_i= Х + Δ_i (i = 1, 2, … n). Поэтому напишем

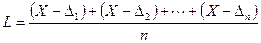= X - .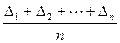

Согласно (5.2) с увеличением числа измерений сумма случайных погрешностей, деленная на их число, стремится к нулю, и, следовательно, среднее арифметическое L стремится к истинному значению Х. Поэтому значение определяемой величины принимают равным среднему арифметическому.

Средняя квадратическая погрешность арифметической средины. Пусть точность результатов измерений l₁, l₂, …, l_n характеризуется средними квадратическими погрешностями

m₁ = m₂ = ¼ = m_n = m

и требуется найти среднюю квадратическую погрешность M арифметической средины.

Представим формулу (5.7) в следующем виде:

L = .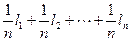

Среднюю квадратическую погрешность арифметической средины найдем как погрешность функции измеренных величин по формуле (5.6)

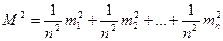
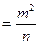
или

(5.8)

Формула (5.8) показывает, что погрешность арифметической средины с ростом числа измерений убывает пропорционально квадратному корню из этого числа. Так, чтобы погрешность среднего арифметического уменьшить в 2 раза, число измерений надо увеличить в 4 раза.

Обработка результатов равноточных измерений. Математическая обработка ряда результатов l₁, l₂, …, l_n прямых равноточных измерений одной величины выполняется в следующей последовательности:

1. Вычисляют среднее арифметическое L

.

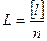2. Вычисляют поправки к v_i результатам измерений

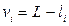(i = 1, 2, …, n)

Контролем правильности вычислений служит сумма поправок, которая должна быть близка к нулю.

3. Вычисляют среднюю квадратическую погрешность одного измерения по формуле Бесселя:

.

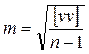Значение m вычисляют с двумя-тремя значащими цифрами.

4. Вычисляют среднюю квадратическую погрешность среднего арифметического

.

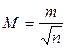5.6 Математическая обработка результатов прямых неравноточных измерений

Веса измерений. Неравноточными называют измерения, выполненные приборами различной точности, разным числом приемов, в различных условиях.

При неравноточных измерениях точность каждого результата измерений характеризуется своей среднеквадратической погрешностью. Наряду со средней квадратической погрешностью при обработке неравноточных измерений пользуются относительной характеристикой точности – весом измерения. Вес i-го измерения вычисляют по формуле

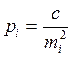(5.9)

где с – произвольная постоянная, назначаемая вычислителем, m_i – средняя квадратическая погрешность i-го измерения.

Так, имея ряд результатов измерений l₁, l₂, ..., l_n , со средними квадратическими погрешностями m₁ , m₂ , ..., m_n , определяют их веса:

p₁ = c / m₁², p₂ = c / m₂² , ..., p_n = c / m_n².

Часто постоянную с для удобства дальнейших вычислений назначают так, чтобы веса p_i оказались целыми числами.

Рассмотрим смысл произвольной постоянной с. Предположим, что в результате фиксирования значения с вес j-го измерения стал равен 1, то есть p_j = c / m_j² = 1. Отсюда находим c = m_j². Следовательно, постоянная с есть квадрат средней квадратической погрешности m² такого измерения, вес которого принят за единицу (с = m²).

Теперь (5.9) можем записать так

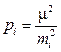. (5.10)

Кратко m называют средней квадратической погрешностью единицы веса.

Вес арифметической средины. Рассмотрим вес арифметической средины равноточных измерений. Примем в формуле (5.8) за единицу вес одного измерения, то есть m = m, и запишем .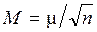

Тогда согласно (5.10) вес Р арифметической средины L будет равен

P = 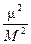= n. (5.11)

Вывод. Если за единицу веса принят вес одного измерения, то согласно (5.11) вес арифметической средины равен числу измерений.

Следствие. Если результат l измерения имеет вес р, то можем считать, что l является средним арифметическим из р измерений с весом 1.

Общая арифметическая средина результатов неравноточных измерений. Пусть имеем результаты многократных неравноточных измерений одной величины: l₁, l₂, …, l_n, выполненных с весами p₁, p₂, …, p_n.

Представим каждый из результатов l_i (i = 1, 2, …, n) как среднее из p_i результатов с весом 1. Получим такой ряд результатов равноточных измерений:

l₁ - результат p₁ измерений с весом 1,

l₂ - результат p₂ измерений с весом 1,

¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼

l_n - результат p_n измерений с весом 1,

где общее число измерений с весом 1 равно p₁ + p₂ +¼+ p_n .

Нами составлен ряд результатов равноточных измерений, позволяющий найти окончательное значение измеряемой величины как среднее арифметическое из всех результатов измерений

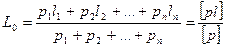. (5.12)

Значение, вычисляемое по формуле (5.12), называют общей арифметической срединой или весовым средним.

Оценки точности результатов неравноточных измерений. Приведем без вывода формулы характеристик точности, используемых при обработке прямых неравноточных измерений.

Средняя квадратическая погрешность m измерения, имеющего вес, равный единице:

- формула Гаусса: .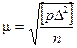

Формула применяется, когда известно достаточно точное, близкое к истинному, значение X измеряемой величины.

- формула Бесселя: ,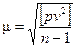

где v_i - поправки к результатам измерений:

.

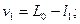
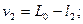
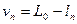Средняя квадратическая погрешность общей арифметической средины

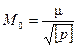
Обработка результатов неравноточных измерений. Математическая обработка ряда результатов прямых неравноточных измерений одной величины выполняется в следующей последовательности.

1. Вычисление весового среднего (общей арифметической средины)

.

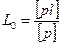2. Вычисление поправок к результатам измерений:

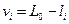(i = 1, 2,…, n).

Контролем правильности вычислений служит равенство

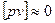
3. Вычисление средней квадратической погрешности одного измерения по уклонениям от арифметической средины, используя формулу Бесселя для неравноточных измерений:

.

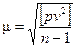4. Вычисление средней квадратической погрешности весового среднего

.

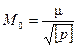5.7. Понятие об уравнивании геодезической сети

При создании геодезической сети всегда измеряют избыточное, то есть большее, чем это необходимо, количество элементов сети (расстояний, углов, превышений). При этом вследствие погрешностей результаты измерений оказываются не согласованными между собой, что проявляется в возникновении угловых, линейных и иных невязок. Для получения согласованных между собой результатов измерений выполняется их математическая обработка, называемая уравниванием.

Так, в плановой сети измеряемые элементы u_i (углы, расстояния) функционально связаны с координатами x, y пунктов сети

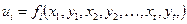
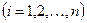. (5.13)

Представим истинные значения u_i как суммы измеренных 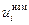и поправок v_i:

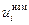u_i = + v_i .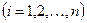

Подставив эти суммы в (5.13), получим систему уравнений

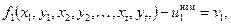
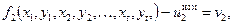
¼¼¼¼¼¼¼¼¼¼¼¼¼

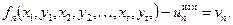
Решением этой системы уравнений находят неизвестные координаты .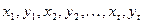

Идеальным решением было бы такое, при котором правые части уравнений стали равны нулю: v₁ = v₂ = ¼ = v_t = 0. Но из-за избыточности числа измерений (n > 2t) и наличия погрешностей результатов измерений система уравнений оказывается несовместной, и решения, обращающего правые части всех уравнений в ноль, не существует.

Вместо идеального решения ищут такое, при котором правые части, то есть поправки к результатам измерений минимальны. При этом обычно применяют метод наименьших квадратов, обеспечивающий отыскание такого решения, при котором сумма квадратов поправок к результатам измерений минимальна:

.

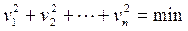Достоинством метода наименьших квадратов по сравнению с другими методами является получение искомых параметров с минимальными средними квадратическими погрешностями.

Дата добавления: 2014-09-10; просмотров: 1424; Нарушение авторских прав

Мы поможем в написании ваших работ!