
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
РИТОРИЧЕСКИЕ ОПЕРАЦИИ
После описания объектов, к которым применяются операции, и контекстов, в которых они возможны, нам надлежит заняться рассмотрением самих этих операций. До сих пор мы объединяли все операции под единым названием «изменения» (altérations), но совершенно очевидно, что за этим термином скрываются несколько различных видов операций. На фоне большой абстрактности всех наших построений операциям, в них участвующим, также должна быть присуща высокая степень общности, они должны принадлежать к числу простейших, фундаментальных операций. Мы будем различать два главных типа операций: субстанциальные и реляционные. Первые
операции меняют субстанцию единиц, к которым они применяются, вторые же меняют только позиционное отношение между этими единицами5.
3.1. Субстанциальные операции
Существуют только два вида таких операций: одни сокращают, вычеркивают (suppriment) единицы в сообщении, другие добавляют (ajoutent) новые единицы к уже существующим. Благодаря механизму членения, подробно описанному выше, любая «трансформация» может быть сведена к сокращению и добавлению единиц. Можно ввести также сложную операцию, одновременно состоящую из сокращения и добавления.
Обозначим буквами A (adjonction) и S (suppression) соответственно операции добавления и сокращения. Мы будем приписывать им числовые индексы, указывающие на число единиц, входящих в поле их действия. Числовое значение индексов не получит здесь развернутой интерпретации: этими вопросами мы займемся на более поздних этапах исследования.
Заметим только, что с увеличением числа сокращенных (или добавленных) единиц количество информации в сообщении соответственно уменьшается (увеличивается). Здесь мы имеем в виду семантическую информацию в смысле Карнапа — Бар-Хиллела: энтропия в этом случае определяется количеством двоичных выборов, необходимых для того, чтобы получить искомую информацию. Именно поэтому, когда речь идет о метасемемах, уровень общности (généralité) сообщения повышается при сокращении или понижается, когда применяется операция добавления: числовой индекс в этом случае указывает на расстояние, пройденное по шкале общности информации. Заканчивая обсуждение этого вопроса, отметим один эмпирически установленный факт: когда речь идет о смешанной операции AmSn, обычно m ≈ n. Таким образом, количество информации и уровень общности в этом случае практически не меняются.
Различные виды общих операций могут распадаться на более частные подвиды. Например, сокращение может
5 Напомним еще раз, что слово «субстанция» в этой главе употребляется в значении, отличном от принятого в глоссематике.
быть частичным (partial) или полным (complet) — в последнем случае n равно количеству единиц более низкого уровня, входящих в значимую единицу, к которой применяется эта операция. Добавление может быть простым (simple) или итеративным (répétif) — если добавляются только значимые единицы нулевой ступени. Что касается смешанных операций, то они могут быть не только частичными или полными, но и отрицающими (négative), когда сокращенная единица заменяется своим отрицанием.
3.2. Реляционные операции
Такие операции проще по своей структуре, поскольку их действие сводится к изменениям линейного порядка значимых единиц, в то время как сами эти единицы не претерпевают каких бы то ни было изменений. Здесь речь идет только о перестановках (permutations), среди которых можно выделить обычные и инвертированные. В последнем случае единицы звуковой или графической последовательности выстраиваются в обратном порядке.
3.3. Графики и таблицы
В таблице VI представлены все те операции, о которых мы говорили выше. Они реализуют все возможности рассматриваемой системы. В этой таблице отражена также совместимость этих операций с тремя группами фигур, которые были описаны выше (раздел 1.1). В частности, из таблицы явствует, что операция отрицания фонемы, графемы, синтаксической конструкции и т. д. лишена всякого смысла, так же как и, впрочем, повтор семы в пределах одной лексемы. Что касается перестановки сем в лексеме, то данная операция невозможна, поскольку этим составляющим присуща иерархическая, а не линейная упорядоченность. По той же причине невозможна перестановка различительных признаков внутри фонемы. Возможность перестановки на уровне предложений вызывает у нас сомнения, хотя гипотеза о существовании логической упорядоченности предложений дает основания предполагать, что такая перестановка в принципе возможна. Что
касается одновременной подмены всех синтаксических констант, то эта операция, как нам кажется, должна быть исключена из рассмотрения.
Проведем прямую с начальной точкой О и отметим на ней число дискретных единиц начиная с О и (по крайней мере теоретически) до бесконечности. Здесь учитывается только количество единиц (индексы m и n), но не их качество. На этом графике любой значимой единице U соответствует точка на прямой:
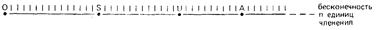
Рис. 3
Таблица VI
Операции и области их применения
| Класс | A | B и C | |||
| Членение | Инфраязыковые единицы (различительные признаки) | Языковые единицы и единицы более высокого уровня | |||
| Означающее | Означаемое | Означающее | Означаемое | ||
| Сокращение | частичное полное | + + | + + | + + | + + |
| Добавление | простое итеративное** | + – | + – | + + | + + |
| Сокращение с добавлением | частичное полное отрицающее* | + + – | + + + | + + – | + + + |
| Перестановка | обычная инвертированная** | – – | – – | + + | + + |
+ = возможно
– = невозможно
* = всегда противопоставляет означающее и означаемое
** = противопоставляет А/В и С, то есть инфраязыковой уровень «всем остальным».
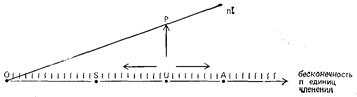
Рис. 4
Положение точки U на прямой будет определяться числом единиц членения n, на которые может быть разложена значимая единица U. Тогда операции А и S могут быть обозначены на прямой точками, лежащими в случае добавления справа, а в случае сокращения — слева от U.
Реляционные операции (перестановки) не влияют на число составляющих значимой единицы: следовательно, они не могут быть представлены на оси, изображенной на рис. 3. Они расположены вертикально относительно оси субстанциальных операций, то есть они не зависят от нее.
Дополняя наше графическое изображение, мы расположим перестановки на прямой, перпендикулярной бесконечной прямой О; полученная система координат будет чем-то напоминать графическое представление комплексных чисел в алгебре. Теоретически возможное число перестановок зависит от числа единиц членения (например, от числа букв в слове, числа слов во фразе) : оно равно n! = n(n — 1) (n — 2) ...3.2.1. Область перестановок Р (permutations) будет, таким образом, ограничена кривой n!, и теперь мы можем получить полное графическое изображение двумерного риторического пространства. Было бы ошибочным считать, что такому изображению нельзя сопоставить содержательную интерпретацию, напротив, на нем прекрасно видно, как «расширяется» пространство по мере того, как растет величина n: чем большее количество единиц получается в результате членения данной значимой единицы, тем большие возможности предоставляет она для риторической обработки.
Общая таблица метабол, или риторических фигур
|
ГРАММАТИЧЕСКИЕ (Код)
 |  |
| ВЫРАЖЕНИЕ | СОДЕРЖАНИЕ | ||||
| СУБСТАНЦИОНАЛЬНЫЕ | А. Метаплазмы | В. Метатаксис | С. Метасемемы | Д. Металогизмы | |
| Операции | Морфологические | Синтаксические | Семантические | Логические | |
| I. Сокращение I. 1. Частичное I. 2. Полное | Аферезис, апокопа, синкопа, синерезис Упразднение, стирание | Стяжение Эллипсис, зевгма, асиндетон, паратаксис | Обобщающие синекдоха и антономазия, сравнение, метафора in praesentia Асемия | Литота 1 Обрыв, приостановка, пауза (умолчание) | |
| II. Добавление II. 1. Простое II. 2. Итеративное | Протеза, диереза, аффиксация, эпентеза, «складное» слово Удвоение, подчеркивание, рифма, аллитерация, ассонанс, парономазия | Вводное слово (предложение), конкатенация, эксплеция, перечисление Реприза, полисиндетон, стихотворный размер, симметрия | Сужающие синекдоха и антономазия, ар-хилексия — | Гипербола, гиперболическая пауза Повторение, плеоназм, антитеза | |
| III. Сокращение с добавлением III. 1. Частичное III. 2. Полное III. 3. Отрицательное | Имитация детской речи, подмена аффиксов, каламбур Синонимия без общей морфологической основы, архаизм, неологизм, создание новых слов, заимствование — | Силлепсис, анаколуф Перевод в другой класс, хиазм — | Метафора in absentia Метонимия Оксюморон | Эвфемизм Аллегория, притча, басня Ирония, парадокс, антифразис, литота 2 | |
| РЕЛЯЦИОНЫЕ | IV. Перестановка IV. 1. Обычная IV.2. Инвертированная | Акрофоническая перестановка, анаграмма, метатеза Палиндром, верлан | Тмезис, гипербатон Инверсия | — — | Логическая инверсия, хронологическая инверсия — |
В обобщающей таблице представлены в качестве примеров фигуры, описание которых читатель может найти в последующих главах, посвященных четырем основным типам метабол.
90-91
| <== предыдущая страница | | | следующая страница ==> |
| I. ОБЩАЯ ТЕОРИЯ ФИГУР | | | МЕТАПЛАЗМЫ |
Дата добавления: 2014-09-10; просмотров: 544; Нарушение авторских прав

Мы поможем в написании ваших работ!