Электрическое поле движущихся зарядов

Для полной характеристики электрического поля, которое создают неподвижные заряды, достаточно задания скалярного потенциала 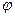. Если заряд движется, то появляется выделенное вектором скорости заряда направление в пространстве. Даже в случае точечного заряда сферическая симметрия поля нарушается. Для описания электрического поля в этом случае необходимо задавать еще одну величину, в которую должен входить вектор скорости, она называется векторным потенциалом 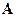. Получить ее из скалярного потенциала, учитывая только геометрию пространства, невозможно. Далее мы обоснуем введение векторного потенциала, используя СТО.

§ 10 Электрическое поле движущегося заряда

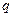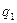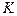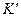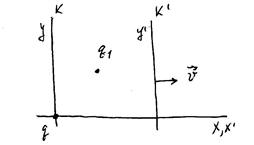
Рассмотрим взаимодействие двух точечных зарядов и в двух системах отсчета - и , вторая движется относительно первой со скоростью 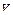(рис.10.1). Пусть в 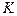системе отсчета заряды неподвижны.

Рис.10.1

Тогда в 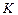- системе отсчета энергия тела с зарядом 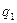равна:

.

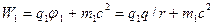Импульс этого тела 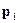в 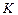- системе отсчета равен нулю. Импульс же этого тела в 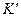- системе отсчета будет равен:

.

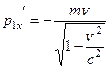Теперь используем правила преобразования энергии и импульса релятивистской частицы при переходе из одной инерциальной системы отсчета в другую (Механика (38.7)):

; .

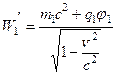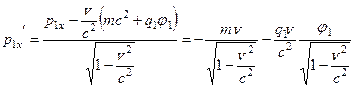Видно, энергия частицы с зарядом 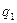в 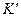- системе отсчета складывается из механической энергии релятивистской частицы и ее энергии в электрическом поле, которая равна:

.

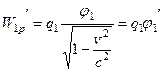Поскольку заряды тел – величины инвариантные, получаем скалярный потенциал в 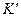- системе отсчета:

.

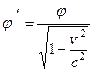Видно, что значение импульса заряженной частицы в 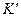- системе отсчета после формального преобразования не совпадает с импульсом не заряженной частицы.

Для того, чтобы избежать этого противоречия в релятивистской физике для заряженных частиц, определяют обобщенный импульс 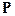следующим образом:

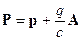, (10.1)

где 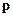- обычный импульс релятивистской частицы, 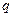- заряд этой частицы, а новая физическая величина 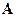называется векторным потенциалом электрического поля в той точке пространства, где находится заряд 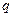(он создается другими движущимися зарядами). Векторный потенциал связан со скалярным потенциалом для поля, создаваемого одним зарядом, следующим образом:

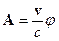. (10.2)

В том случае, который мы рассматриваем, векторный потенциал в 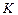- системе отсчета равен нулю, а в 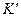- системе отсчета в той точке, где находится заряд 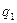, он равен

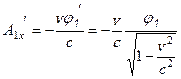
(подчеркнем, что он создается движущимся зарядом 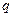). Тогда обобщенный импульс тела с зарядом 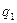будет равен:

.

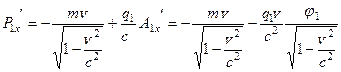Получили результат, совпадающий с тем, который дают формальные преобразования 4-импульса частицы при переходе из одной инерциальной системы отсчета в другую.

Итак, для заряженных частиц обобщаем понятие импульса и тогда правила преобразования обобщенного 4-импульса остаются теми же, что мы определили для незаряженных релятивистских частиц (Механика (38.7)).

Для описания же электрического поля движущегося заряда необходимо задавать скалярный потенциал 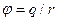и векторный потенциал .

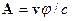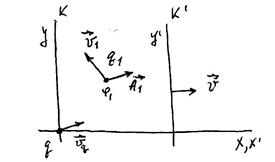
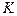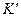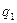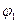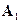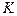Теперь определим, как меняется скалярный и векторный потенциал электрического поля при переходе из в систему отсчета (рис.10.2) в том случае, когда заряженные частицы движутся в обеих системах отсчета. На рисунке движущийся заряд показан в точке, электрическое поле в которой характеризуется скалярным потенциалом и векторным потенциалом в системе отсчета.

Итак, компоненты обобщенного 4-импульса заряженной частицы

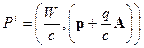(10.3)

Рис.10.2

преобразуются так же, как компоненты 4-радиус-вектора. Для энергии частицы с зарядом 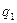в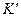системе отсчета получаем:

.

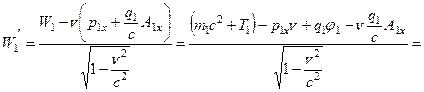
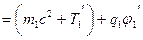Поскольку для механической энергии справедливо соотношение (Механика (38.7)):

,

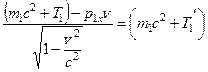для преобразования потенциала получаем следующее правило:

.

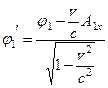Делая аналогичные преобразования для других компонент 4-вектора 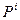, можем получить правила преобразования векторного потенциала 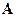. Сделайте это самостоятельно и сравните с результатом, который мы получим, воспользовавшись определением (10.2) и правилами преобразования скоростей (Механика (35.2,35.3)). Для 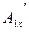проекции получим:

.

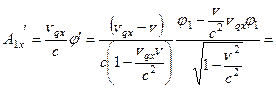
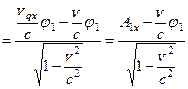В свою очередь для проекции 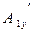получим:

.

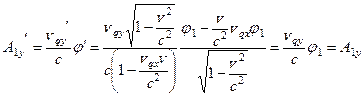Аналогичный результат получим и для 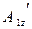проекции.

Видим, что скалярный потенциал и компоненты векторного потенциала преобразуются так же, как и компоненты 4-радиус-вектора. Поэтому скалярный и векторный потенциалы мы можем объединить в один 4-вектор, называемый 4-потенциалом электрического поля:

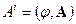(10.4)

Выпишем еще раз правила преобразования компонент этого 4-потенциала при переходе из 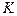в 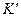систему отсчета, которая движется вдоль оси х со скоростью :

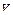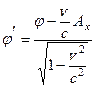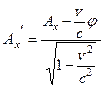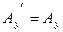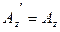, , , . (10.5)

Как для скалярного, так и для векторного потенциала справедлив принцип суперпозиции, который обобщается и на 4-потенциал. Если электрическое поле создается 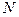точечными зарядами, то потенциал поля в любой точке пространства (за исключением тех, в которых находятся заряды) равен сумме потенциалов полей, созданных каждым зарядом в отдельности.

Для скалярного потенциала справедливо соотношение (4.3), а векторный потенциал будет равен:

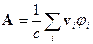, (10.6)

где суммирование проводится по всем зарядам, создающим поле. В произвольной точке пространства соотношение (10.2) между скалярным и векторным потенциалом уже не выполняется, если поле создают несколько зарядов, а не один заряд.

Дата добавления: 2014-02-26; просмотров: 571; Нарушение авторских прав

Мы поможем в написании ваших работ!