
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЕ МАТЕМАТИЧЕСКОГО МАЯТНИКА И ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ
ЦЕЛЬ РАБОТЫ: изучить законы колебательного движения , определить ускорения силы тяжести.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: математический маятник, секундомер, набор шариков, линейка.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Движение, при котором тело или система тел через равные промежутки времени отклоняется от положения равновесия и вновь возвращается к нему, называются периодическими колебаниями.
Колебания, при которых изменение колеблющейся величины со временем происходит по закону синуса или косинуса, называются гармоническими.
Уравнение гармонического колебания записывается в виде:
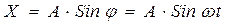
Гармонические колебания характеризуются следующими параметрами: амплитудой А, периодом Т, частотой υ, фазой φ, круговой частотой ω.
А – амплитуда колебания – это наибольшее смещение от положения равновесия. Амплитуда измеряется в единицах длины ( м, см и т. д.).
Т – период колебания – это время, в течении которого совершается одно полное колебание. Период измеряется в секундах.
υ – Частота колебания – это число колебаний, совершаемых в единицу времени. Измеряется в Герцах.
φ – фаза колебания. Фаза определяет положение колеблющейся точки в данный момент времени. В системе СИ фаза измеряется в радианах.
ω – круговая частота измеряется рад/с
Всякое колебательное движение совершается под действием переменной силы. В случае гармонического колебания эта сила пропорциональна смещения и направлена против смещения:
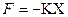 ,
,
где К – коэффициент пропорциональности, зависящий от массы тела и круговой частоты.

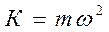


Примером гармонического колебания может служить колебательной движение математического маятника.
Математическим маятником называют материальную точку, подвешенную на невесомой и недеформируемой нити.
Небольшой тяжелый шарик, подвешенный на тонкой нити (нерастяжимой), является хорошей моделью математического маятника.
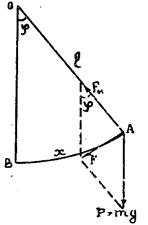
Рис.1
Пусть математический маятник длиной l (рис. 1) отклонен от положения равновесия ОВ на малый угол φ ≤ 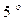 . На шарик действует сила тяжести
. На шарик действует сила тяжести 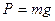 , направленная вертикально вниз, и сила упругости нити
, направленная вертикально вниз, и сила упругости нити 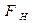 , направленная вдоль нити. Равнодействующая этих сил F будет направлена по касательной к дуге АВ и равна:
, направленная вдоль нити. Равнодействующая этих сил F будет направлена по касательной к дуге АВ и равна:
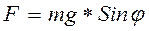
При малых углах φ можно записать:
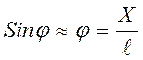
где Х – дуговое смещение маятника от положения равновесия. Тогда получим:
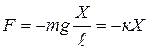
Знак минус указывает на то, что сила F направлена против смещения Х.
Итак, при малых углах отклонения математический маятник совершает гармонические колебания. Период колебаний математического маятника определяется формулой Гюйгенса:
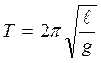
где 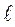 - длина маятника, т. е. расстояние от точки подвеса до центра тяжести маятника.
- длина маятника, т. е. расстояние от точки подвеса до центра тяжести маятника.
Из последней формулы видно, что период колебания математического маятника зависит лишь от длины маятника и ускорения силы тяжести и не зависит от амплитуды колебания и от массы маятника. Зная период колебания математического маятника и его длину, можно определить ускорение силы тяжести по формуле:
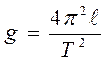
Ускорением силы тяжести называется то ускорение, которое приобретает тело под действием силы притяжения его к земле.
На основании второго закона Ньютона и закона всемирного тяготения можно записать:
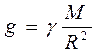
где  γ – гравитационная постоянная, равная
γ – гравитационная постоянная, равная 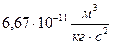
М – масса Земли, равна 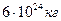 ,
,
R – расстояние до центра Земли, равное 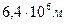 ,
,
Т. к. Земля не имеет форму правильного шара, то на различных широтах имеет разное значение, а, следовательно, и ускорение силы тяжести на разных широтах будет разное: на экваторе 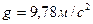 ; на полюсе
; на полюсе 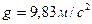 ; на средней широте
; на средней широте 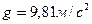 .
.
2. Описание экспериментальной установки:
Лабораторная установка для изучения колебательного движения математического маятника и определение ускорения силы тяжести представлена на рисунке 2.
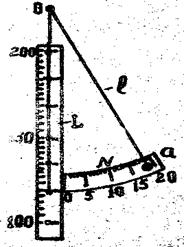
Рис.2
Тяжелый шарик подвешен на длинной нити ℓ. Нить перекинута через кольцо О и вторым своим концом закреплена на шкале L. Перемещая конец нити по шкале, можно изменить длину маятника ℓ, значение которой сразу же определяется по шкале. Для определения углового отклонения маятника служит шкала N. Закрепляя на нити различные шарики, можно изменить массу маятника. Таким образом, в лабораторной установке предусмотрена возможность изменения длины, амплитуды колебания и массы маятника.
3. Порядок выполнения работы:
1. Установите длину маятника ℓ 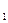 и с помощью секундомера определите время t
и с помощью секундомера определите время t 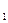 , в течении которого совершается n колебаний. Время измеряется три раза и берется среднее значение.
, в течении которого совершается n колебаний. Время измеряется три раза и берется среднее значение.
2. Опыт повторить для длин ℓ 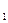 и ℓ
и ℓ 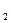 . (Длина маятника и число колебаний задается преподавателем).
. (Длина маятника и число колебаний задается преподавателем).
3. Вычислите среднее значение t 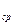 и период колебания Т,
и период колебания Т, 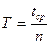 .
.
4. Вычислите ускорение силы тяжести для каждой длины маятника по формуле: 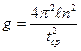
5. Рассчитайте ошибки измерений. Средняя относительная ошибка измерения ускорения силы тяжести вычисляется по формуле:
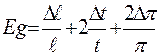 ,
,
где Δℓ - средняя абсолютная ошибка измерения длины маятника.
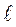 - длина маятника.
- длина маятника.
Δt – средняя абсолютная ошибка измерения времени.
t – время в течении которого маятник совершает n колебаний.
6. Данные эксперимента занесите в таблицы 1 и 2.
7. Сделайте выводы.
Таблица 1
Определение ускорения силы тяжести
| №№ п/п | Число колебаний | Длина маятника
ℓ 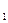 = (см) = (см)
| Длина маятника
ℓ 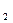 = (см) = (см)
| Длина маятника
ℓ 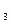 = (см) = (см)
| ||||||
| n (с) | t, c | Т, с | 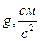
| t, c | T, c | 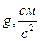
| t, c | T, c | 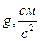
| |
| 1. | ||||||||||
| 2. | ||||||||||
| 3. | ||||||||||
| Сред |
Таблица 2
Расчет ошибок измерений
| Длина | ℓ 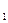 = (см) = (см)
| ℓ 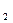 = (см) = (см)
| ℓ 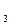 = (см) = (см)
| |||||||||
| Ошибки изм. | Δt, c | Δℓ, см | Eg, % | Dg, см/с 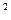
| Δt, c | Δℓ, см | Eg, % | Dg, см/с 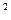
| Δt, c | Δℓ, см | Eg, % | Dg, см/с 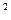
|
| 1. | ||||||||||||
| 2. | ||||||||||||
| 3. | ||||||||||||
| Сред. |
4. Контрольные вопросы:.
1. Дайте определение гармонического колебания и его основных характеристик.
2. Запишите уравнение гармонического колебания.
3. Что такое физический маятник? Запишите формулу периода колебания физического маятника.
4. Что такое математический маятник? Запишите формулу периода колебания математического маятника.
ЛАБОРАТОРНАЯ РАБОТА №3
| <== предыдущая страница | | | следующая страница ==> |
| Определение плотности тела | | | ИЗУЧЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА |
Дата добавления: 2014-09-29; просмотров: 853; Нарушение авторских прав

Мы поможем в написании ваших работ!