ИЗУЧЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА

ЦЕЛЬ РАБОТА: изучить и проверить на практике основной закон вращательного движения.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: маятник Обербека, секундомер, технические весы, разновесы, штангенциркуль, рулетка.

1. Краткие теоретические сведения:

Вращательным движением твердого тела называется такое движение, при котором все точки тела движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения.

При вращательном движении твердого тела линейные скорости будут различны для точек, расположенных на разном расстоянии от оси вращения, а угловая скорость будет для всех точек одинакова. Это же самое можно сказать и о линейном и угловом ускорениях.

Величина угловой скорости может быть определена как отношение угла 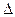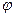поворота радиуса (т. е. отношение углового пути) к промежутку времени, за который этот поворот произошел (см. рис. 1):

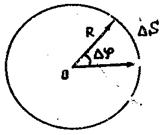
Рис.1

В системе СИ угловая скорость измеряется в рад/ с.

При неравномерном движении материальной точки по окружности вместе с линейной скоростью изменяется и угловая скорость. Поэтому вводится понятие углового ускорения, которое измеряется в рад/ с² и равно:

Линейные и угловые величины связаны формулами:

,

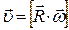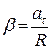
Тело совершает вращательное движение под действием момента вращающей силы М=F R . В системе СИ момент силы измеряется в Н м.

Инерционные свойства вращающегося тела характеризуются моментом инерции. Моментом инерции материальной точки называется произведение ее массы на квадрат расстояния до оси вращения.

J =m R²

Момент инерции тела равен сумме моментов инерции всех материальных точек, составляющих тело.

Вращательное движение подчинятся основному закону динамики вращения: момент вращающей силы, приложенный к телу, равен произведению момента инерции тела на угловое ускорение:

M = J·β

2. Описание экспериментальной установки:

В данной работе проверка основного закона вращательного движения осуществляется с помощью маятника Обербека.

Маятник Обербека представляет собой крестовину из четырех стержней, расположенных под углом 90^о друг к другу, прикрепленных к цилиндру с осью вращения О (см. рис. 2).

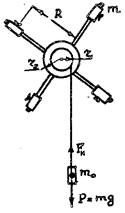
Рис.2

На эту же ось насаживают два шкива с различными диаметрами. На стержни надевают одинаковые грузы m, которые с помощью винтов можно закрепить их на любом расстоянии от оси вращения. Маятник приводится во вращательное движение грузом m_о, прикрепленным к концу нити, намотанной на шкив. На груз m_о действует сила тяжести P=mg, направленная вертикально вниз, и сила натяжения нити F_н, направленная вдоль нити вверх. Результирующая сила будет направлена вниз. Под действием этой результирующей силы груз будет двигаться равноускоренно с ускорением α. Для всей системы можно записать уравнение:

m_o α = m_og – F_н,

где сила натяжения нити

F_н=m_o(g – α),

Сила натяжения нити создает вращающий момент, под действием которого маятник совершает ускоренное вращательное движение.

Вращательный момент равен

M = m_or(g – α),

где m_o - масса груза,

r – радиус шкива,

g – ускорение свободного падения,

Ускорение находится по формуле:

α = ,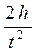

где h –высота, с которой падает груз,

t – время падения груза.

Так как нить сматывается со шкива без скольжения, то линейное ускорение точек поверхности шкива равно ускорению падающего груза. Тогда для углового ускорения шкива имеем:

β=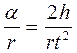

3. Порядок выполнения работы:

ЗАДАНИЕ 1: установление связи между моментами вращающих сил и соответствующими им угловыми ускорениями при неизменном моменте инерции, т. е.

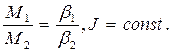
1. Снимите со стержней дополнительные грузы m.

2. Определите массу падающего груза m_o.

3. Измерьте радиусы шкивов r₁ и r₂.

4. Намотайте нить на малый шкив и определите с помощью секундомера время падения груза с заданной высоты.

5. Опыт проведите три раза и найдите среднее значение времени t₁.

6. Намотайте нить на большой шкив и определите время падения груза. Опыт повторите три раза и найдите среднее значение t₂.

7. Вычислите линейные ускорения по формулам: 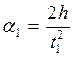и .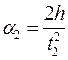

8. Вычислите угловое ускорение по формулам: 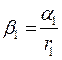и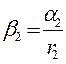

9. Вычислите моменты сил по формулам:

M₁=m_or₁(g – α); M₂=m_or₂(g – α₂)

Проверьте равенство:

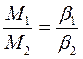
10. Вычислите момент инерции крестовины по формуле:

= .

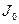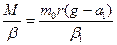11.Данные эксперимента занесите в таблицу 1:

Таблица 1

Результаты эксперимент

№ п/п

m0, г

h, см

t1

t2

r1

r2

М1

М2

J0, г·см2

β1, с

β2, с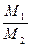

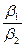
с

см

Дн*см

Сред.

ЗАДАНИЕ 2: установление связи между угловыми ускорениями и соответствующими им моментами инерции при постоянном моменте силы, т.е.

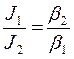, M = const.

1. Определите массу одного из дополнительных грузов m.

2. Закрепите грузы на стержни на расстоянии 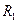от центра вращения, (расстояние 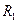задается преподавателем).

3. Намотайте нить на один из шкивов и определите время падения 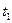груза 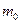с высоты h.

4. Закрепите груз на стержне на расстоянии, 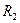(расстояние 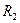задается преподавателем).

5. Определите время падения груза 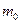с этой высоты h.

6. Вычислите угловые ускорения:

,

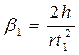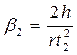
7. Вычислите моменты инерции маятника при различных положениях грузов m по формулам:

;

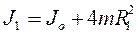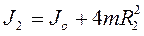
8. Проверьте равенство

9. Данные эксперимента занесите в таблицу 2:

Таблица 2:

Результаты эксперимента

№ п/п

m, г

h, см

r, см

R1, см

R2, см

T1, см

t2, см

J1

J2

β1

β2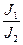

г*см2

с-2

1. 2. 3.

сред

10. На основании результатов двух экспериментов сделайте выводы.

4. Контрольные вопросы:.

1. Что такое момент вращающей силы? В чем он измеряется?

2. Сформулируйте основной закон динамики вращающего движения. Что такое момент инерции тела?

3. Что такое линейная и угловая скорости, линейное и угловое ускорения? Какова связь между этими величинами?

4. Есть ли аналогия между формулами поступательного и вращательного движения?

ЛАБОРАТОРНАЯ РАБОТА №4

Дата добавления: 2014-09-29; просмотров: 917; Нарушение авторских прав

Мы поможем в написании ваших работ!