
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ИЗ РАСТЯЖЕНИЯ И ИЗГИБА
ЦЕЛЬ РАБОТЫ: исследование упругих свойств материала, проверка закона Гука и определение модуля Юнга.
1. Краткие теоретические сведения:
При действии сил на тело изменяется его форма, т. е. говорят что тело деформируется. Деформации возникают всегда при действии силы, однако, в одних случаях они не значительны и малозаметны, в других – их величина имеет большое значение. Различают деформации кручения, сдвига, растяжения, сжатия и изгиба. Во многих задачах механики необходимо знать законы, связывающие различные деформации с вызывающими их силами. Однако, законы, связывающие силы и деформации, в общем случае очень сложны и не являются предметом нашего рассмотрения. Рассмотрим простейший случай – деформации в упругом теле, или деформацию растяжения одного стержня длиной ℓ0 (рис. 1).
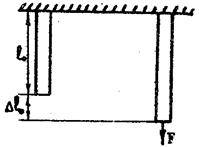 Рис.1
Рис.1
Пусть верхний конец стержня закреплен на опоре, а к нижнему – приложена сила F. Стержень деформируется, т. е. растянется на величину Δℓ0. Относительно удлинения стержня будет 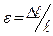 Оно будет зависеть от величины растягивающей силы F. Под действием силы в стержне нарушается равновесие внутренних сил (межатомных, межмолекулярных). В каждом сечении стержня появляются отличные от нуля результирующие внутренних сил, направленные против внешней силы F. В момент уравновешивания внешних сил внутренними деформациями тела достигает определенной величины и больше не изменяются. Следовательно, в условиях равновесия величина внутренних упругих сил может быть измерена величиной внешних сил, приложенных к телу.
Оно будет зависеть от величины растягивающей силы F. Под действием силы в стержне нарушается равновесие внутренних сил (межатомных, межмолекулярных). В каждом сечении стержня появляются отличные от нуля результирующие внутренних сил, направленные против внешней силы F. В момент уравновешивания внешних сил внутренними деформациями тела достигает определенной величины и больше не изменяются. Следовательно, в условиях равновесия величина внутренних упругих сил может быть измерена величиной внешних сил, приложенных к телу.
Внешняя сила, действующая на единицу площади поперечного сечения тела, называется напряжением и обозначается 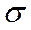 . Напряжение в растягиваемом стержне будет равно:
. Напряжение в растягиваемом стержне будет равно:
 ,
,
где S – площадь поперечного сечения стержня.
Опыт показывает, что относительная деформация 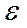 определяется напряжением. Связь между деформацией и напряжением можно изобразить графически (рис. 2). Как видно из рисунка линейная зависимость
определяется напряжением. Связь между деформацией и напряжением можно изобразить графически (рис. 2). Как видно из рисунка линейная зависимость 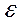 от
от 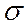 выполняется в узком диапазоне приложенных напряжений (до точки П). Предельное значение напряжений, при котором еще соблюдается линейная зависимость напряжения от деформации, называется пределом пропорциональности. Область деформации, соответствующих участку кривой, начинающемуся от точки У, называется областью пластической деформации. После точки Р. кривая спадает и обрывается, что соответствует разрушению образца, т. е. пределу прочности тела.
выполняется в узком диапазоне приложенных напряжений (до точки П). Предельное значение напряжений, при котором еще соблюдается линейная зависимость напряжения от деформации, называется пределом пропорциональности. Область деформации, соответствующих участку кривой, начинающемуся от точки У, называется областью пластической деформации. После точки Р. кривая спадает и обрывается, что соответствует разрушению образца, т. е. пределу прочности тела.
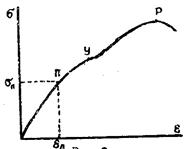
рис.2
В данной работе нас будет интересовать только упругие деформации. Из рисунка видно, что до точки П кривая 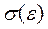 представляет собой прямую линию, т. е. зависимость между напряжением и деформацией можно представить простым законом:
представляет собой прямую линию, т. е. зависимость между напряжением и деформацией можно представить простым законом:
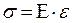 или
или 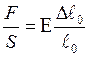
Это соотношение выражается законом Гука: относительное удлинение 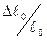 прямо пропорционально приложенному напряжению (т. е. растягивающему усилию на единицу площади
прямо пропорционально приложенному напряжению (т. е. растягивающему усилию на единицу площади 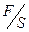 ).
).
Коэффициент Е носит название модуля Юнга. Для стали величина Е.=2*106кг/см2 – 2*1011Н/м2, а для алюминия Е.=7*1010Н/м2.
Из формулы один следует физический смысл модуля Юнга E.
При Δ 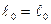 модуль Юнга E= F/S =
модуль Юнга E= F/S = 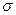 , т.е. модуль Юнга равен напряжению, которое возникало бы в образце при увеличении его длины в 2 раза, если бы при столь большой деформации был бы справедлив закон Гука. В реальных случаях разрушение образца наступает значительно быстрее, чем будет достигнуто удлинение Δ
, т.е. модуль Юнга равен напряжению, которое возникало бы в образце при увеличении его длины в 2 раза, если бы при столь большой деформации был бы справедлив закон Гука. В реальных случаях разрушение образца наступает значительно быстрее, чем будет достигнуто удлинение Δ 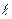 0=
0= 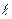 0т.е. относительные увеличения тел при деформациях как правило, очень малы.
0т.е. относительные увеличения тел при деформациях как правило, очень малы.
ЗАДАНИЕ 1 : Определение модуля Юнга из растяжения.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ : прибор Лермонтова, проволока из исследуемого материала, измерительный микроскоп МИР-2, набор грузов, микрометр, измерительная линейка / рулетки /.
ОПИСАНИЕ ЭКСПЕРЕМЕНТАЛЬНОЙ УСТАНОВКИ.
Для определения модуля Юнга в данной работе используется прибор Лермонтова /рис.3/. Исследуемая проволока своим верхним концом крепится к кронштейну 1, а нижним – соединена со стержнем площадки 2, на которую можно перекладывать грузы с площадки 3, и тем самым изменять напряжение проволоки. Такая система позволяет в течение всего опыта поддерживать на верхнем кронштейне 1 постоянную нагрузку, равную суммарному весу грузов на площадках 2 и 3. В результате этого исключается влияние деформации кронштейна 1 на точность измерений. На конце кронштейна 4 крепится измерительный микроскоп МИР-2 для отсчета величины удлинения проволоки по шкале 6, которая закрепляется на конце испытуемой проволоки.
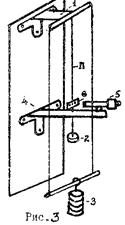
При проведении эксперимента следует иметь в виду, что растяжение проволоки рассчитано на строго определенный груз, который в исходном состоянии сосредоточен на площадке 3, т.е. площадка 2 должна быть разгружена. Увеличивать нагрузку на площадке 2 более предусмотренного в работе опасно, так как при этом можно выйти из области применимости закона Гука.
Порядок выполнения работы:
1. Измерите длину проволоки ℓ0 линейкой (рулеткой).
2. Определить диаметр проволоки d микрометром не менее чем в пяти местах и найти среднее из всех измерений dср и найдите площадь по сечения S
3. Познакомьтесь с отсчетным микроскопом МИР – 2.
4. Установите длину тубуса микроскопа 160 мм, что соответствует цене деления шкалы микроскопа 0,045 мм.
5. Направьте микроскоп на измерительную метку 6 и получите ее четкое изображение в поле зрения микроскопа.
6. Снимите зависимость удлинения проволоки Δℓ0 от нагрузки при возрастающей и уменьшающейся нагрузках.
Результаты исследований занесите в таблицу 1.
Результаты эксперимента.
| № п/п | Увеличение нагрузки | Уменьшение нагрузки | ||||
| m, кг | n, дел. | Δℓ0, мм | m, кг | n, дел. | Δℓ0, мм | |
7. Постройте график координатах Р.(Δℓ0) и убедитесь в совпадении прямых при увеличении и уменьшении нагрузки на проволоку, где P =mg.
8. Вычислите среднее удлинение проволоки Δℓ0 при действии на нее одного груза Р.
9. Определите величину Е. по формуле:
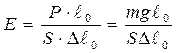
10. Вычислите относительную ошибку полученного результата по формуле:
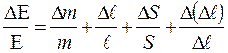
11. Запишите полученный результат и сделайте выводы.
Задание 2: Определение модуля Юнга из изгиба.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ прибор для исследований упругих свойств стержня, стержень из исследуемого материала, набор грузов штангенциркуль, измерительная линейка.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ:
В данной работе изучается простейший случай деформации – деформация изгиба. Из рисунка 4 видно, что данная деформация сводится к неоднородным деформациям сжатия и растяжения. Для определения модуля Юнга Е., характеризующего эти деформации, в теории упругости выводиться формула /2/,пользуясь которой можно определить значение E для стержня прямоугольного сечения с помощью легко измеряемых на опыте величин:
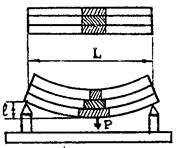
Рис.4
где K= 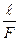
l- стрела прогиба, м
F - величина нагрузки;
L- расстояние между опорами при м, м ;
B - ширина стержня , м ;
H- толщина стержня , м.
Формула выведена в предположении, что ребра опорных призм параллельны, а прогибающая сила приложена в середине стержня.
Экспериментальная установка /рис.5/ состоит из массивной стальной балки 1 со стойками 2. На концах стоек установлены опорные призмы 3, на которые опирается исследуемый стержень 4.К середине исследуемого стержня крепится держатель с площадкой 5, на которую навешиваются грузы 6.Изгиб стержня определяется с помощью индикатора часового типа 7 или с помощью микрометрического винта с электрической системой индикации.
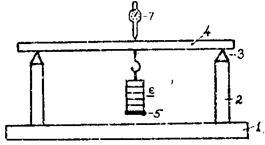
Рис.5
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Измерьте линейкой расстояние между ребрами призм L.
2. Определите ширину B и толщину H стержня штангенциркулем.
3. Результаты измерений величин L, B, H занесите в таблицу 1.
Таблица 1.
Результаты измерений L, B, H
| L | B | H | DL | DB | DH |
4. Исследуемый стержень установите на опорные призмы и к ее середине подвесьте площадку для грузов.
5. Приведите в соприкосновение с центром исследуемого стержня измерительный конец индикатора или микрометрического винта и запишите их начальные положения при нулевом значении нагрузки на стержне.
6. Снимите зависимость величины прогиба стержня от величины нагрузки P=mg при увеличении и уменьшении нагрузки. Результаты занесите в таблицу 2.
Таблица 2
Результаты измерений
| № п/п | m, г | n1, мм | n2, мм | ℓ1, мм | ℓ2, мм | 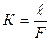
| 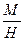
|
Обозначения в таблице 2:
m -массы грузов;
n1-показания микрометрического винта или индикатора при увеличении нагрузки до максимальной;
n2 -показания при уменьшении нагрузки от максимальной до полной разгрузки стержня;
l1 -величина прогиба стержня при увеличении нагрузки;
l2 -то же при уменьшении нагрузки;
l –полное значение прогиба стержня при грузе P.
7.По данным таблицы 2 постройте график зависимости величины прогиба от величины нагрузки при увеличении и уменьшении нагрузки и сделайте выводы.
8.Определить модуль Юнга E по формуле /2/.
9.Оцените погрешность измерений по формулам:
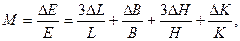 %;
%;
DE= M*E, Н/м2
10.Запишите полученный результат и сделайте выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ:.
1.Какие деформации вы знаете?
2.Сформулируйте закон Гука.
3.Каков физический смысл модуля Юнга?
4.Расскажыте об устройстве экспериментальных установок.
ЛАБОРАТОРНАЯ РАБОТА № 5
| <== предыдущая страница | | | следующая страница ==> |
| ИЗУЧЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА | | | ОПРЕЛЕЛЕНИЕ СКОРОСТИ ЗВУКА МЕТОДОМ СТОЯЧЕЙ ВОДЫ |
Дата добавления: 2014-09-29; просмотров: 1461; Нарушение авторских прав

Мы поможем в написании ваших работ!