Термодинамические потенциалы

Критериями направления процесса и состояния равновесия в системе являются термодинамические потенциалы. В изолированных системах таким термодинамическим потенциалом является энтропия. Рассмотрим далее процессы в открытых и закрытых системах.

Вспомним математические формулировки I и II начал термодинамики:

dQ = dU + dA (2.23)

dQ £ TdS (2.24)

Объединим эти уравнения:

TdS ³ dU + dA (2.25)

Представим работу как сумму полезной работы А' и работы расширения РdV:

dA = d 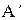+ РdV (2.26)

Подставим (2.27) в (2.26):

TdS ³ dU + d 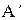+ РdV (2.27)

или

- d 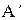³ dU - TdS + РdV (2.28)

Для равновесного процесса 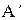= 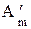, а в (2.28) остается только знак “=“ :

- d 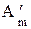= dU - TdS + РdV (2.29)

При Р,Т - const уравнение (2.30) можно представить в виде:

-d 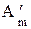= d(U-TS+РV) или (2.30)

-d 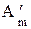=d(H-TS) (2.31)

а при V,T - const:

-d 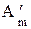=d(U-TS) (2.32)

Из уравнений (2.30) - (2.32) следует, что в указанных условиях полезная работа обратимых процессов равна изменению некоторых функций состояния системы, а именно, при P,T - const

-d 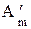= dG_P,T , (2.33)

где G = U -TS + РV (2.34)

или

G = Н -TS (2.35)

а при V,T -const

-d 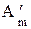= dF_V,T, (2.36)

где F= U-TS (2.37)

Из сравнений (2.34) и (2.37):

G = F + РV (2.38)

Функция G называется энергией Гиббса, или изобарно-изотермическим потенциалом, или просто изобарным потенциалом.

Функция F называется энергией Гельмгольца, или изохорно-изотер-мическим потенциалом, или просто изохорным потенциалом.

Как следует из приведенного выше вывода, изобарный и изохорный потенциалы являются функциями состояния системы при постоянстве указанных параметров.

Функции Гиббса и Гельмгольца являются важнейшими термодинамическими характеристиками процессов в указанных условиях и широко используются в анализе термодинамической вероятности процессов.

Покажем далее, каким образом используют данные термодинамические потенциалы в качестве критериев возможности осуществления различных процессов. Из уравнений (2.33) и (2.36), обобщённо для обратимых и необратимых процессов:

dG_P,T £ -d (2.39)

dF_V,T £ -d (2.40)

Физический смысл функций Гиббса и Гельмгольца состоит в том, что они составляют ту долю энергии системы, которая может переходить в полезную работу.

Существует множество процессов, в которых единственным видом работы является работа расширения, а полезная работа =0 (например, при химической реакции).

Для таких систем:

dG_P,T £ 0, DG_P,T£ 0 (2.41)

dF_V,T £ 0, DF_V,T£ 0 (2.42)

Из этих неравенств следует, что при необратимом самопроизвольном процессе в изобарно-изотермических условиях изобарный потенциал системы уменьшается, а в условиях равновесия остается постоянным и минимальным (dG_P,T =0). Аналогично при V, T - const в состоянии равновесия dF_V,T = 0, а при необратимом самопроизвольном процессе F уменьшается.

Изобразим графически эти критерии направления процесса и состояния равновесия в системе, приведя здесь же рассмотренный ранее критерий для изолированных систем (энтропия), рис. 2.2.

Изменение функций Гиббса и Гельмгольца в ходе процессов, протекающих в условиях постоянства соответствующих параметров, на основании уравнений (2.34), (2.35) и (2.37), можно рассчитать по термодинамическим данным процесса (т.е. зная тепловой эффект процесса при постоянном давлении, или, иначе говоря, - изменение энтальпии, а также изменение энтропии и внутренней энергии):

P, T = const V, T = const U, V = const

G F S

A C A C В

B B A C

путь процесса

Рис.2.2. Критерии направления процесса и состояния равновесия.

АВ - необратимый самопроизвольный процесс

ВС - необратимый не самопроизвольный процесс

(·)В - состояние равновесия.

DG_P,T = DU - TDS + pDV (2.43)

или DG_P,T = DH - TDS (2.44)

и DF_V,T = DU -TDS (2.45)

Из последнего уравнения выразим DU:

DU = DF + TDS (2.46)

Анализ этого уравнения показывает, что изменение внутренней энергии при Т = const для обратимого процесса складывается из свободной энергии DF (которая может быть превращена в полезную работу) и связанной энергии ТDS (которая может выделяться или поглощаться в виде теплоты).

Приведенные выше уравнения позволили составить таблицы стандартных величин DG⁰₂₉₈ и DF⁰₂₉₈ для многих веществ. Они относятся, как и энтальпии, к реакциям образования данного химического соединения при стандартных условиях из химических элементов, взятых в стандартном состоянии.

Расчеты значений свободной энергии Гиббса для любой гипотетической реакции позволяют судить о возможности ее осуществления в данных изобарно-изотермических условиях, способности данных веществ вступать в химическую реакцию. Это определяет широту использования энергии Гиббса для анализа природных и искусственных химических процессов.

Энергию Гиббса, в связи с этим, называют мерой химического сродства.

Дата добавления: 2014-10-02; просмотров: 535; Нарушение авторских прав

Мы поможем в написании ваших работ!