
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Характеристические функции. Уравнения Гиббса-Гельмгольца
В предыдущем разделе мы рассмотрели энергию Гиббса и Гельмгольца в качестве термодинамических потенциалов, т.е. в условиях постоянства параметров Р, Т и V, T соответственно, когда эти функции определяют направление процесса и состояние равновесия в системе. Не менее важна роль функций Гиббса и Гельмгольца в условиях, когда указанные параметры (Р, Т и V, T) являются переменными. В этом случае с помощью функций Гиббса и Гельмгольца можно выражать в явном виде различные термодинамические свойства систем, характеризуя таким образом состояние системы, поэтому их называют в этих условиях характеристическими функциями.
Получим наиболее важные уравнения для ряда термодинамических параметров системы (V, P, S), выразив их через функции Гиббса и Гельмгольца.
По определению [уравнение (2.34)], энергия Гиббса:
G = U + РV – TS (2.50)
Продифференцируем уравнение (2.50), считая все параметры переменными:
dG = dU + РdV + VdP – TdS – SdT (2.51)
Из объединенного уравнения I и II законов термодинамики для равновесных процессов
dU = TdS – РdV (2.52)
Подставив (2.52) в (2.51), получим:
dG = VdP – SdT (2.53)
Аналогично для функции Гельмгольца можно получить:
dF = - РdV - SdТ (2.54)
Из уравнений (2.53) и (2.54) следует, что
G = f(T,P) (2.55)
F = f(T,V) (2.56)
Точно так же можно выразить функции
U = f(S,V) (2.57)
H = f(S,P) (2.58)
Переменные, от которых зависят указанные функции называются их естественными переменными.
Запишем полные дифференциалы функций (2.55) и (2.56):
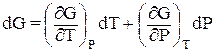 (2.59)
(2.59)
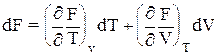 (2.60)
(2.60)
Сопоставив (2.53) и (2.59), а также (2.54) и (2.60), получим:
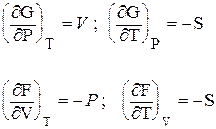 (2.61)
(2.61)
Таким образом, с помощью функций Гиббса и Гельмгольца мы выразили в явном виде ряд важнейших термодинамических параметров.
Запишем уравнения (2.61) через изменения функций Гиббса и Гельмгольца в ходе процесса:
 (2.62)
(2.62)
Подставив полученные выражения в уравнения (2.44) и (2.45) для изотермических процессов, получим:
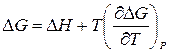
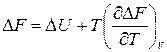 (2.63)
(2.63)
Уравнения (2.63) называются уравнениями Гиббса - Гельмгольца. Они используются при выводе многих термодинамических уравнений. Мы будем применять их далее при рассмотрении влияния температуры на состояние химического равновесия. Заметим, что уравнения Гиббса - Гельмгольца связывают максимальную полезную работу процесса с тепловым эффектом, т.к. при Р,Т - const DH = QP и  , а при V,T – const DU = QV и
, а при V,T – const DU = QV и 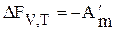 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Свободная энергия Гиббса и закономерности появления самородных элементов | | | Химический потенциал. Активность |
Дата добавления: 2014-10-02; просмотров: 438; Нарушение авторских прав

Мы поможем в написании ваших работ!