
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Химический потенциал. Активность
При протекании многих процессов, например в ходе химических реакций, состав системы меняется. В этом случае энергии Гиббса и Гельмгольца являются функциями не только своих естественных переменных, но и числа молей реагентов, ni :
G=f(T,P,n1,n2....ni) (2.64)
F=f(T,V, n1,n2....ni) (2.65)
Возьмем полный дифференциал функции G:
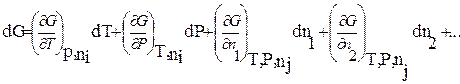 (2.66)
(2.66)
Индекс ni в уравнении (2.66) указывает на постоянство числа молей всех компонентов, а  - всех, кроме данного.
- всех, кроме данного.
Aналогично можно выразить и функцию Гельмгольца.
Величина
 (2.67)
(2.67)
есть парциальный молярный изобарный потенциал данного компонента.
При постоянных Р и Т Gi имеет смысл химической энергии и называется химическим потенциалом компонента i (mi):
mi º 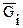 =
= 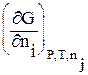 (2.68)
(2.68)
Химический потенциал - одна из важнейших термодинамических функций, широко применяемая при изучении состояний равновесия в различных термодинамических системах. Ее ввел Дж. Гиббс в 1887 г.
Физический смысл химического потенциала:
Химический потенциал компонента i равен приращению изобарного потенциала при добавлении одного моля этого компонента к большому объему системы при постоянных Р и Т. Понятие «большой объем» означает, что состав системы не меняется при добавлении 1 моля компонента.
Введем в уравнение (2.66) принятое обозначение (2.68) и запишем его при условии Р, Т=const:
dGP,T= m1dn1+m2dn2+....
или dGP,T = 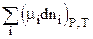 (2.69)
(2.69)
В состоянии равновесия dGP,T=0, тогда
 (2.70)
(2.70)
Уравнение (2.70) есть общее условие равновесия в системе переменного состава. Мы будем пользоваться им при рассмотрении химических и фазовых равновесий.
Условием самопроизвольного протекания процесса является dG<0, следовательно
 (2.71)
(2.71)
Неравенство (2.71) есть общее условие возможности самопроизвольного протекания процесса в системе переменного состава.
Химический потенциал можно выразить и через другие термодинамические функции (F, U, H) при постоянстве их естественных переменных (соответственно, V, T; S, V и S, P). Мы будем рассматривать далее преимущественно условия Р, Т -const как наиболее часто реализуемые в реальных системах.
Любые равновесные свойства веществ можно выражать через химический потенциал.
Получим выражение для химического потенциала 1 моля идеального газа. С учетом (2.53):
dm = dG = VdP – SdT (2.72)
При T = const dm = VdP (2.73)
Из уравнения состояния 1 моля идеального газа:
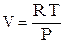 (2.74)
(2.74)
Подставив (2.74) в (2.73), получим:
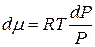 (2.75)
(2.75)
Проинтегрируем уравнение (2.75) в пределах интегрирования от стандартного давления Р0 до Р и, соответственно, от стандартного значения химического потенциала m0 до его значения m при давлении Р:
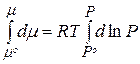 (2.76)
(2.76)
m = m0 + RTln(P/Р0) (2.77)
Здесь m0 - стандартный химический потенциал 1 моля идеального газа, то есть химический потенциал, соответствующий значению Р = Р0. Иначе стандартный химический потенциал можно определить как химический потенциал при относительном давлении (P/Р0) равном единице. В физической химии стандартным давлением считается давление Р0= 1,013·105 Па. В этом случае, вычисляя относительное давление, следует Р выражать в тех же единицах. В то же время, за стандартное может быть принята величина Р0 = 1атм. Тогда и давление Р при вычислении относительной величины должно быть выражено в атмосферах. Таким образом, под знаком логарифма всегда должна быть безразмерная величина. Далее будем обозначать относительные давления 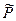 .
.
Уравнение (2.77) справедливо и для компонента i идеальной газовой смеси:
mi = mi0 + RTln 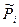 (2.78)
(2.78)
В этом случае 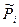 - относительное парциальное давление компонента i в идеальной газовой смеси.
- относительное парциальное давление компонента i в идеальной газовой смеси.
Общее давление в идеальной газовой смеси равно сумме парциальных давлений компонентов.
Аналогично можно получить для компонента идеального раствора:
mi=mi0 + RTln  (2.79)
(2.79)
Здесь  - отношение концентрации (молярной доли) компонента i в растворе к стандартной концентрации, равной единице.
- отношение концентрации (молярной доли) компонента i в растворе к стандартной концентрации, равной единице.
Тогда стандартный химический потенциал компонента i в растворе, mi0 , соответствует относительной концентрации компонента i в растворе, равной единице.
Для вычисления химических потенциалов в реальных, то есть неидеальных газах и растворах, Г. Льюис предложил величины Pi и Ni заменять, соответственно, фугитивностью fi (fugacity - летучесть) и активностью аi. Выражая их относительными величинами, можно получить:
mi = mi0 + RTln  (2.80)
(2.80)
mi = mi0 + RTln  (2.81)
(2.81)
где 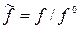 , (2.82)
, (2.82)
 - стандартная фугитивность реального газа, которая считается равной стандартному давлению;
- стандартная фугитивность реального газа, которая считается равной стандартному давлению;
 , (2.83)
, (2.83)
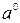 - стандартная активность, которую принимают равной единице.
- стандартная активность, которую принимают равной единице.
Отношение фугитивности к давлению реального газа называется коэффициентом фугитивности:
 ;
; 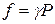 (2.84)
(2.84)
Отношение активности компонента в растворе к его концентрации называется коэффициентом активности:
 ;
;  (2.85)
(2.85)
Коэффициенты фугитивности и активности – безразмерные величины. Они учитывают отклонение свойств реальных систем от идеальных в связи с наличием межмолекулярных взаимодействий в реальных системах. При низких давлениях и низких концентрациях межмолекулярные взаимодействия малы, и свойства реальных систем приближаются к свойствам идеальных, а коэффициенты gi ® 1 и fi ® Pi ; ai ® Ni .
Фугитивность и коэффициент фугитивности зависят от температуры, давления и состава газовой смеси. В зависимости от условий  может быть как меньше единицы, так и больше. Как правило, межмолекулярные взаимодействия в реальных газах начинают сказываться при давлениях 50-100 атм и выше, при этом преобладают силы отталкивания и наблюдаются значительные отклонения от уравнения состояния идеальных газов. Вместо парциальных давлений тогда приходится пользоваться для практических расчётов величинами фугитивностей, при этом они могут значительно отличаться от парциальных давлений, и коэффициент фугитивности может быть много больше единицы.
может быть как меньше единицы, так и больше. Как правило, межмолекулярные взаимодействия в реальных газах начинают сказываться при давлениях 50-100 атм и выше, при этом преобладают силы отталкивания и наблюдаются значительные отклонения от уравнения состояния идеальных газов. Вместо парциальных давлений тогда приходится пользоваться для практических расчётов величинами фугитивностей, при этом они могут значительно отличаться от парциальных давлений, и коэффициент фугитивности может быть много больше единицы.
Активности чистых индивидуальных веществ равны единице, поэтому химический потенциал 1 моля чистого твердого или жидкого вещества при Р,Т - const есть величина постоянная, равная стандартному потенциалу данного вещества m0.
При рассмотрении термодинамических свойств различных систем мы очень часто будем пользоваться выражениями для химических потенциалов.
Для термодинамических расчетов необходимы сведения о термодинамических свойствах веществ. Они публикуются во многих специальных статьях, монографиях, справочниках. Некоторые из них приведены в списке литературы.
| <== предыдущая страница | | | следующая страница ==> |
| Характеристические функции. Уравнения Гиббса-Гельмгольца | | | Уравнение изотермы химической реакции. Константа химического равновесия |
Дата добавления: 2014-10-02; просмотров: 669; Нарушение авторских прав

Мы поможем в написании ваших работ!