
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Геомагнитный потенциал. Формализм Гаусса
Уравнения магнитостатики в той части пространства, где отсутствуют токи, в дифференциальной форме имеют вид:
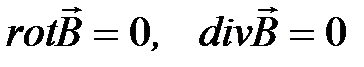 .
.
Следуя тому, что изложено в п. 3.1, можно заключить, что магнитное поле Земли вне источников, которые его создают, потенциально, т.е.
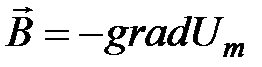 .
.
Геомагнитный потенциал удовлетворяет уравнению Лапласа 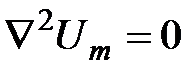 , фундаментальным решением которого в сферических координатах является сферический гармонический ряд
, фундаментальным решением которого в сферических координатах является сферический гармонический ряд
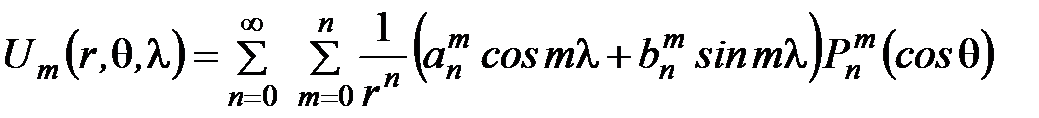 .
.
При 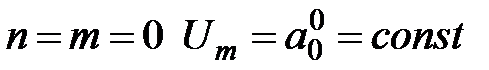 . Положим
. Положим 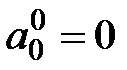 , что эквивалентно предположению об отсутствии магнитных зарядов.
, что эквивалентно предположению об отсутствии магнитных зарядов.
Нормируем радиальное расстояние к среднему радиусу Земли R и введем обозначения:
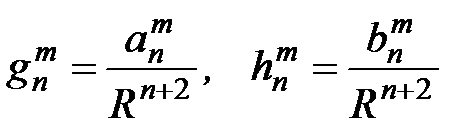 .
.
Тогда
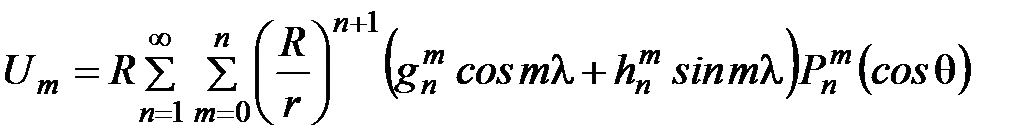 .
.
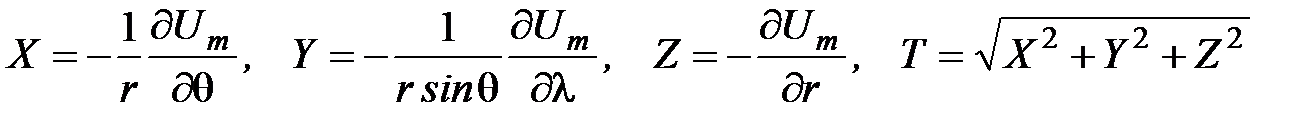 .
.
Итак, имея значения элементов земного магнетизма в некотором числе точек, можно вычислить некоторое конечное число коэффициентов 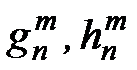 (обратная задача), и представить геомагнитный потенциал в виде конечного ряда, дифференцируя который можно получить значения элементов в любых точках поверхности Земли и над ее поверхностью (прямая задача).
(обратная задача), и представить геомагнитный потенциал в виде конечного ряда, дифференцируя который можно получить значения элементов в любых точках поверхности Земли и над ее поверхностью (прямая задача).
В этом, собственно, и состоит формализм Гаусса. Коэффициенты 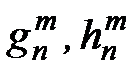 , имеющие размерность индукции магнитного поля, называют гауссовыми коэффициентами.
, имеющие размерность индукции магнитного поля, называют гауссовыми коэффициентами.
Легко видеть, что если в выражении для геомагнитного потенциала ограничиться гармониками порядка n, то число гауссовых коэффициентов будет равно n(n+2). Для их нахождения нужно иметь столько же уравнений. Чтобы уменьшить влияние экспериментальных ошибок, используют большее число уравнений, т.е. решают переопределенную систему уравнений. Гаусс разработал метод решения переопределенных неоднородных систем алгебраических уравнений, который получил название «метод наименьших квадратов» (МНК).
Суть МНК в следующем. Пусть A – матрица коэффициентов размером 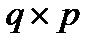 (q – число строк, p – число столбцов, q>p), x – вектор-столбец p неизвестных, b – вектор-столбец q известных величин. Применительно к обратной задаче геомагнетизма: A – это матрица, составленная из произведений
(q – число строк, p – число столбцов, q>p), x – вектор-столбец p неизвестных, b – вектор-столбец q известных величин. Применительно к обратной задаче геомагнетизма: A – это матрица, составленная из произведений 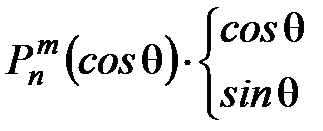 и их производных в заданных точках земной поверхности, x – вектор-столбец p = n(n+2) неизвестных коэффициентов
и их производных в заданных точках земной поверхности, x – вектор-столбец p = n(n+2) неизвестных коэффициентов  , b – вектор-столбец q измеренных в заданных точках значений компонент поля. Переопределенная система уравнений в матричной форме запишется так:
, b – вектор-столбец q измеренных в заданных точках значений компонент поля. Переопределенная система уравнений в матричной форме запишется так:
A∙x = b.
К квадратной форме она приводится путем умножения слева на транспонированную матрицу AT.
AT∙A∙x = AT∙b.
Эту систему далее можно решать методом, который тоже разработал Гаусс. Матричное же решение имеет вид x = (AT∙A)–1 ∙(AT∙b) и обладает тем свойством, что │x –x0 │2 = min, где x0 – истинное решение.
Сам Гаусс, ограничившись членами четвертого порядка (n = 4, n(n+2) = 24), решал систему из 36 уравнений (в его распоряжении были данные наблюдений в 12 обсерваториях). Современные вычисления гауссовых коэффициентов основываются на решении десятков тысяч уравнений, и эти коэффициенты вычисляются до n ~ 15–20.
Дома: Найти решение системы уравнений:
2 x + y +z = 5
x – y + z = 2
x + 2 y – z = 4
3 x –y + z = 3
2 x + 2 y – 3 z = 1 Ответ: 1,180; 1,297; 1,365
Для примера выпишем несколько первых коэффициентов разложения геомагнитного потенциала в ряд по сферическим функциям для эпохи 1973.0. Единицы измерения гауссовых коэффициентов – нанотеслы (нТл).
| n | |||||
| m | |||||
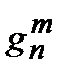
| –30356 | –2148 | –1642 | ||
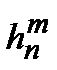
| –1973 |
Покажем, что первые три члена сферического гармонического ряда описывают магнитное поле диполя, помещенного в начало сферической системы координат (в центр Земли). Эти первые три члена на поверхности Земли следует записать в виде:
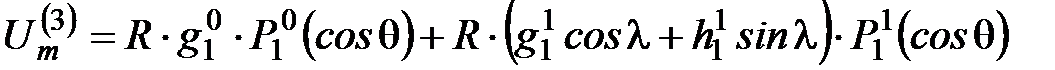 .
.
Известно, что потенциал магнитного диполя с моментом 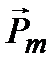 имеет вид:
имеет вид:
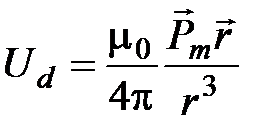 ,
,
где 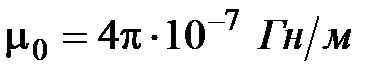 . Заметим, что точно такой же потенциал имеет и однородно намагниченный шар. Магнитный момент шара равен
. Заметим, что точно такой же потенциал имеет и однородно намагниченный шар. Магнитный момент шара равен 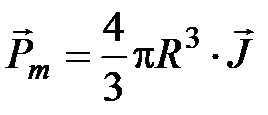 , где R – радиус шара, а
, где R – радиус шара, а 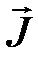 – его намагниченность.
– его намагниченность.
Магнитное поле диполя 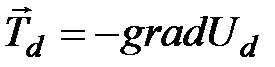 симметрично относительно оси диполя. В сферической системе координат, в которой ось диполя совпадает с направлением полярной оси, компоненты вектора
симметрично относительно оси диполя. В сферической системе координат, в которой ось диполя совпадает с направлением полярной оси, компоненты вектора 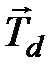 имеют вид:
имеют вид:
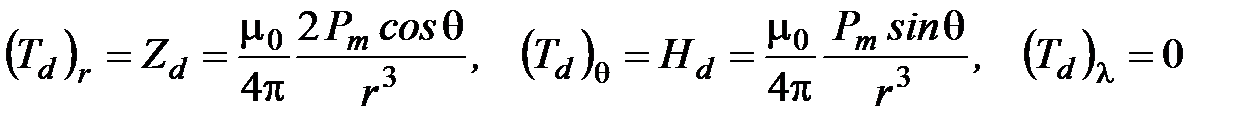 .
.
| N |
| θ |
| λ |
| λ0 |
| y |
| θ0 |
| B |
| A |
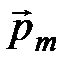
|
| N1 |
Предположим, что в центре Земли находится магнитный диполь с моментом
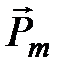 , ось которого пересекает поверхность Земли в точке A с координатами
, ось которого пересекает поверхность Земли в точке A с координатами 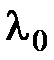 (долгота) и
(долгота) и 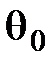 (коширота). Определим потенциал поля, создаваемый диполем в
(коширота). Определим потенциал поля, создаваемый диполем в
точке 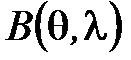 (см. рис.).
(см. рис.).
Для сферического треугольника ANB по теореме косинусов имеем:
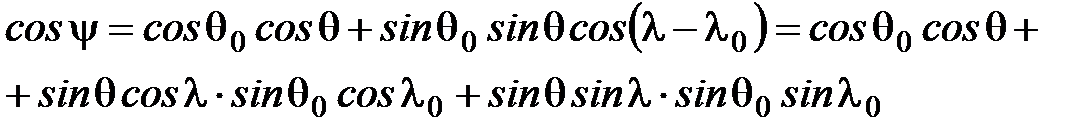
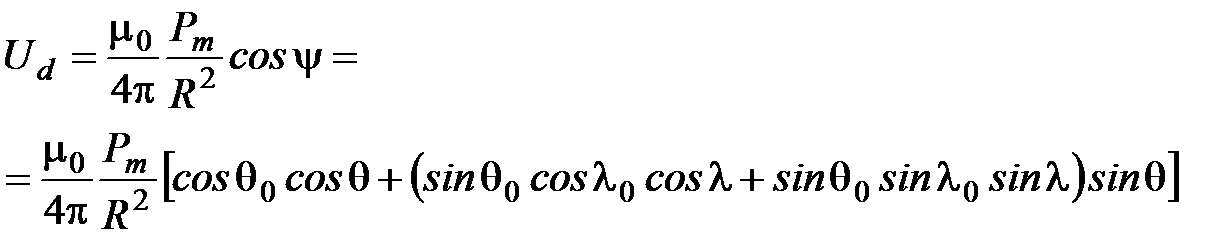
Введем обозначения для констант:
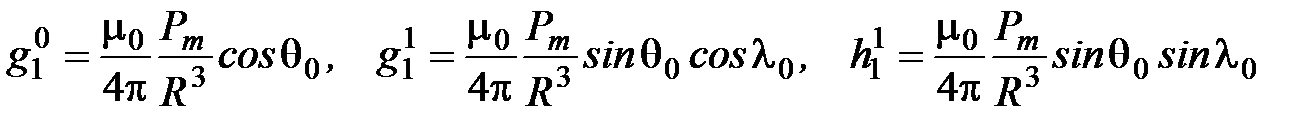 .
.
Тогда
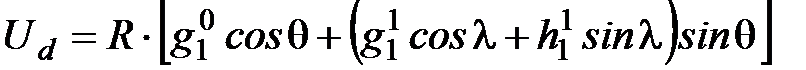 .
.
Поскольку 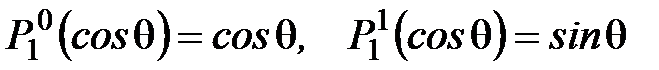 , то первые члены сферического гармонического ряда представляют собой потенциал, создаваемый центральным магнитным диполем или однородно намагниченным шаром. Члены второго порядка (n = 2) интерпретируют как квадрупольные компоненты потенциала, члены третьего порядка – как октупольные компоненты, и т.д.
, то первые члены сферического гармонического ряда представляют собой потенциал, создаваемый центральным магнитным диполем или однородно намагниченным шаром. Члены второго порядка (n = 2) интерпретируют как квадрупольные компоненты потенциала, члены третьего порядка – как октупольные компоненты, и т.д.
Легко видеть, что если 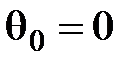 , то диполь ориентирован вдоль оси NN1 (вдоль оси вращения Земли). Из приведенной выше таблицы следует, что осевая составляющая геомагнитного диполя преобладает. Коэффициенты
, то диполь ориентирован вдоль оси NN1 (вдоль оси вращения Земли). Из приведенной выше таблицы следует, что осевая составляющая геомагнитного диполя преобладает. Коэффициенты 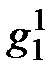 и
и 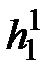 определяют экваториальную составляющую диполя. В сумме три первых коэффициента дают более 80% всего геомагнитного поля. В первом приближении земное магнитное поле – это поле центрального диполя, наклоненного под некоторым углом к оси вращения.
определяют экваториальную составляющую диполя. В сумме три первых коэффициента дают более 80% всего геомагнитного поля. В первом приближении земное магнитное поле – это поле центрального диполя, наклоненного под некоторым углом к оси вращения.
По известным значениям 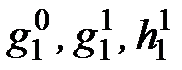 нетрудно вычислить величину геомагнитного диполя и координаты пересечения его с поверхностью Земли.
нетрудно вычислить величину геомагнитного диполя и координаты пересечения его с поверхностью Земли.
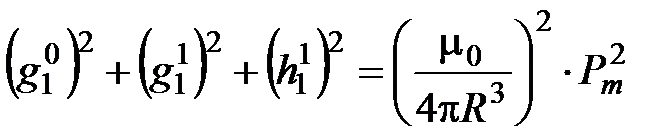 .
.
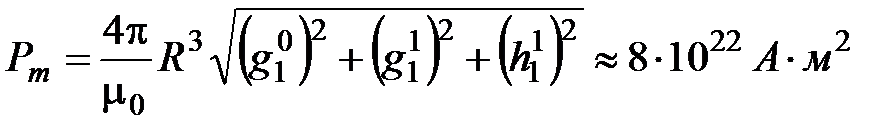 .
.
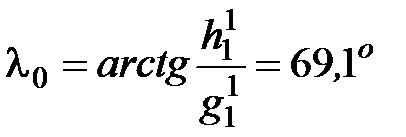 з.д.
з.д.
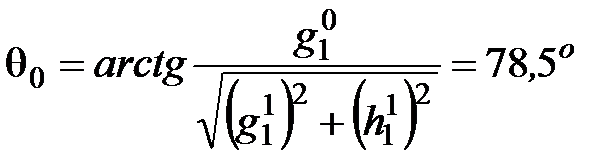 с.ш.
с.ш.
Это координаты геомагнитного полюса в северном полушарии на эпоху 1973.0. В 1905 г. координаты геомагнитных полюсов были: 78,60 с.ш., 68,70 з.д. и 78,60 ю.ш., 111,30 в.д. В 2005 г. координаты были: 79,70 с.ш., 71,80 з.д. и 79,70 ю.ш., 108,20 в.д. Как видно из этих данных, дипольный магнитный момент Земли имеет наклон порядка 10-110 к оси вращения Земли и медленно поворачивается относительно этой оси.
Главное магнитное поле Земли (ГМПЗ) имеет дипольный характер только в первом приближении. Дипольность ГМПЗ отчетливо проявляется только при наблюдениях (измерениях) на значительном удалении от поверхности Земли в силу того, что дипольная составляющая магнитного поля убывает пропорционально 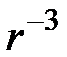 , квадрупольная составляющая убывает по закону
, квадрупольная составляющая убывает по закону 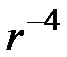 и т.д.
и т.д.
| <== предыдущая страница | | | следующая страница ==> |
| МАГНИТНОЕ ПОЛЕ ЗЕМЛИ | | | История геомагнитного поля |
Дата добавления: 2014-08-04; просмотров: 619; Нарушение авторских прав

Мы поможем в написании ваших работ!