
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Нормальное распределение Гаусса
Если признак имеется в среднем у 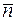 частиц, причем выполняется
частиц, причем выполняется 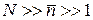 , то вероятность признака у n частиц при относительно малом отклонении от среднего
, то вероятность признака у n частиц при относительно малом отклонении от среднего 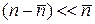 описывается нормальным распределением
описывается нормальным распределением
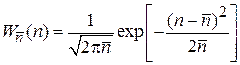 . (1.19)
. (1.19)
Результат получил Гаусс в 1809 г.

Карл Фридрих Гаусс (1777–1855)
Доказательство
Условие 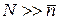 означает
означает  и выполнение распределения Пуассона
и выполнение распределения Пуассона
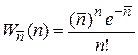 .
.
Логарифмируем
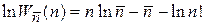 .
.
Используем формулу Стирлинга (рассматривается в курсе ММФ)
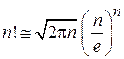 , при
, при 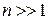 ,
,
которая дает
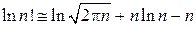 .
.
Получаем
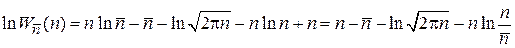 .
.
Вводим отклонение от среднего 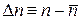 , тогда
, тогда
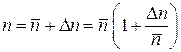 .
.
Для распределения Гаусса учитываем 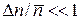 . Разлагаем
. Разлагаем 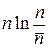 по степеням малой величины
по степеням малой величины 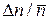 и сохраняем лишь первые два слагаемые, считая остальные несущественными:
и сохраняем лишь первые два слагаемые, считая остальные несущественными:
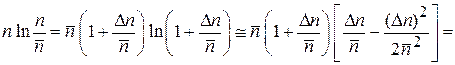
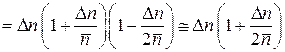 .
.
Находим
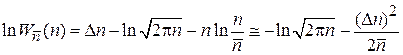 .
.
Потенцируем результат и, используя 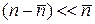 , заменяем
, заменяем 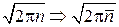 , и получаем (1.19)
, и получаем (1.19)
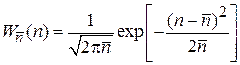 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Частные и рекуррентные соотношения | | | Условие нормировки |
Дата добавления: 2014-02-27; просмотров: 417; Нарушение авторских прав

Мы поможем в написании ваших работ!