Граничные условия

На граничной поверхности раздела сред параметры скачкообразно изменяются. При этом, согласно выражениям (1.10): 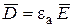, , , 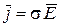неизбежно испытывают скачки некоторые векторы поля. Для решения задач электродинамики, помимо уравнений Максвелла, необходимо знать граничные условия – соотношения между векторами поля в двух очень близких точках, находящихся по обе стороны границы раздела двух сред. Граничные условия являются следствием уравнений Максвелла в интегральной форме для этого особого случая.

Вектор поля с произвольной ориентацией может быть представлен геометрической суммой двух составляющих: касательной и нормальной к граничной плоскости (рисунок 1.1). Определим соотношения между касательными составляющими векторов поля двух сред и нормальными составляющими.

· Граничные условия для касательных составляющих векторов поля

Предположим, что имеются две однородные среды, разделенные граничной поверхностью (рисунок 1.2), на которой могут возникать поверхностные электрические заряды, а также поверхностные электрические токи (то есть токи, текущие в бесконечно тонком поверхностном слое).

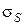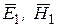Распределение зарядов и токов на границе будем характеризовать поверхностной плотностью заряда и вектором поверхностной плотности тока . Обозначим векторы поля в первой и второй средах и 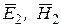соответственно и найдем связь между ними.

Построим контур , пересекающий поверхность (рисунок 1.2). Применяя к этому контуру первое и второе уравнения Максвелла в интегральной форме, получаем

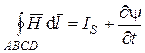, (1.36)

, (1.37)

где 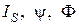– соответственно ток, электрический поток и магнитный поток через поверхность контура.

Если стороны и 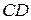прижимать к границе так, что площадь обращается в ноль, то в пределе . Однако величина , при наличии на поверхностных токов, в нуль не обращается, ибо деформированный (сжатый) контур все равно будет охватывать ток.

Пусть расстояние от точки до точки равно 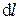. Вводя далее вектор 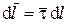, где – орт касательной к стороне сжатого контура, из уравнения (1.36), получаем

,

где – орт нормали к поверхности контура.

Отсюда следует, что на поверхности

, но ,

тогда

или .

Учитывая, что

,

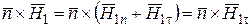получаем

. (1.38)

Таким образом, при переходе через границу с поверхностным током касательная составляющая вектора 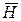испытывает скачок. Величина этого скачка равна поверхностной плотности тока . Если поверхностных токов на граничной поверхности нет, то равенство (1.38) принимает вид

,

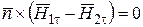откуда вытекает, что

. (1.39)

Во второе уравнение Максвелла электрические токи непосредственно не входят, поэтому независимо от того, есть или нет поверхностный ток, из (1.37) получаем

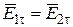. (1.40)

На границе раздела реальных сред касательные составляющие векторов и 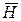всегда непрерывны.

· Граничные условия для нормальных составляющих векторов поля

Рассмотрим на границе раздела сред , которая в общем случае может быть заряжена с поверхностной плотностью 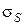, площадку настолько малой величины, чтобы можно было положить равномерно распределенными на ней заряд и векторы поля (рисунок 1.3). Затем построим цилиндр высотой так, чтобы рассматриваемая площадка представляла его поперечное сечение. Тогда, применяя к области, заключенной в цилиндре, третье уравнение Максвелла (1.31), получаем

. (1.41)

Рисунок 1.3 – К выводу граничных условий для нормальных

составляющих векторов поля

Поток вектора через замкнутую поверхность цилиндра состоит из потоков через основания цилиндра в первой и второй 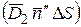средах и потока через всю боковую поверхность цилиндра - , то есть

.

Устремим высоту цилиндра к нулю 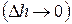. Тогда поток через боковую поверхность , так как поверхность . При этом также , а . Следовательно, при условии, что 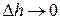будем иметь

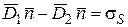или ,

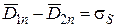. (1.42)

Нормальная составляющая вектора электрической индукции при переходе через граничную поверхность претерпевает скачок, численно равный поверхностной плотности электрического заряда. Поверхностный заряд может образоваться на поверхности проводника в электростатическом поле. В переменном электромагнитном поле такие заряды возможны лишь на поверхности идеальных проводников. Поэтому при переменных полях в реальных средах нормальная составляющая вектора электрической индукции на границе не меняется

или .

Используя четвертое уравнение Максвелла для магнитной индукции (1.34), рассуждая аналогичным образом, получаем

или .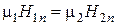

Нормальные составляющие векторов магнитной индукции на границе раздела сред равны друг другу.

Дата добавления: 2014-10-10; просмотров: 473; Нарушение авторских прав

Мы поможем в написании ваших работ!