Энергия электромагнитного поля

Энергия представляет собой количественную меру движения материи. Закон сохранения энергии – один из фундаментальных законов природы. Явления электромагнетизма подчиняются ему без всяких исключений. В равной степени электромагнитное поле подчиняется закону сохранения массы, связанной с энергией формулой Эйнштейна , и закону сохранения импульса.

Энергия, сосредоточенная в произвольном объеме может изменяться во времени, вследствие:

· перехода внутри объема электромагнитной формы движения материи в другие формы: тепловую, механическую, химическую и другие. Для электромагнитного поля это равнозначно потерям. Скорость отдачи энергии электромагнитным полем называется мощностью его потерь ;

· приобретение электромагнитным полем внутри объема энергии от сторонних источников. При этом скорость увеличения энергии поля равна мощности сторонних сил ;

· пересечения электромагнитными волнами, переносящими определенную энергию, граничной поверхности . В этом случае электромагнитная форма движения материи сохраняется. Поток электромагнитных волн из некоторого объема будем называть излучением. Мощность излучения .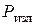

По закону сохранения энергии, введенные величины должны быть связаны соотношением

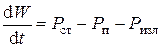. (1.43)

Теорема Умова-Пойнтинга о сохранении энергии в электромагнитном поле

В произвольном объеме электромагнитного поля сосредоточен запас энергии, равный

. (1.44)

С изменением электрического и магнитного полей во времени объемная плотность электрической энергии и объемная плотность магнитной энергии меняются. Для того чтобы выяснить, что происходит с общим запасом энергии, найдем из уравнений Максвелла значения производных и

;

.

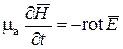Умножая первое из написанных равенств скалярно на , а второе на 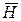и складывая их, получаем

. (1.45)

Но

; ,

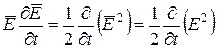а согласно тождеству

,

уравнение (1.45) можно записать в виде

,

или, интегрируя по объему и меняя знаки на обратные, будем иметь

. (1.46)

Используя теорему Остроградского-Гаусса, преобразуем первый интеграл правой части (1.46) по поверхности , ограничивающей рассматриваемый объем

.

Тогда, обозначая

, (1.47)

получаем

. (1.48)

Уравнение (1.48) выражает собой закон сохранения энергии в электромагнитном поле. Рассмотрим его физическое содержание. Левая часть уравнения представляет собой скорость изменения во времени полного запаса электромагнитной энергии в рассматриваемом объеме с обратным знаком . Первый член правой части представляет собой потери мощности в проводящих частях объема . Второе слагаемое в правой части – поток вектора плотности энергии, протекающего через поверхность в единицу времени. Таким образом,

. (1.49)

Согласно определению вектора (1.47), энергия электромагнитного поля в каждой точке движется по нормали к плоскости, образованной векторами и 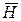, в сторону, совпадающую с поступательным движением правовинтового штопора, вращаемого от вектора к вектору 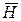на наименьший угол.

Уравнение (1.49) утверждает, что изменение запаса электромагнитной энергии в произвольном объеме обусловлено, во-первых, превращением части ее в тепло (при конечной проводимости среды) и, во-вторых, движением энергии в пространстве через поверхность, ограничивающую объем. Рассматриваемое уравнение имеет наименование теоремы Умова-Пойнтинга.

Это наименование дано в честь известного русского ученого Н.А. Умова, впервые поставившего и исследовавшего вопрос о потоках энергии любого вида в различных средах, и в честь английского физика Пойнтинга, исследовавшего эти же вопросы применительно к электромагнитному полю.

Вектор получил название вектора Пойнтинга.

Дата добавления: 2014-10-10; просмотров: 843; Нарушение авторских прав

Мы поможем в написании ваших работ!