
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОПИСАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
1.1. Силовые векторы электромагнитного поля
Электромагнитное поле характеризуется силами, действующими на заряды. Эти силы являются векторами. Поэтому электромагнитное поле описывается с помощью системы векторов.
На заряд, находящийся в электромагнитном поле, действует сила Лоренца:
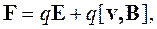
| (1.1) |
| где | q | - величина заряда частицы, взаимодействующей с полем, Кл; |
| Е | - вектор напряженности электрического поля, В/м; | |
| v | - вектор скорости движения заряженной частицы, м/с; | |
| В | - вектор магнитной индукции, Т. |
Векторы напряженности электрического поля и магнитной индукции описывают силы, действующие на заряды в электромагнитном поле, поэтому они называются силовыми.
Формула (1.1) наглядно показывает, что все проявления электромагнитного поля делятся на две группы явлений - электрические и магнитные. Поэтому обычно выделяют две составляющие электромагнитного поля - электрическое поле и магнитное поле.
Формула (1.1) подчеркивает еще один важный факт. Электрическое поле действует на любые заряды, движущиеся и неподвижные, а магнитное – только на движущиеся.
Таким образом, можно сформулировать следующие определения силовых векторов электромагнитного поля.
Вектором напряженности электрического поля называется сила, действующая на единичный электрический заряд:
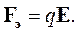
| (1.2) |
Вектором магнитной индукции называется сила, действующая на единичный заряд, движущийся с единичной скоростью:
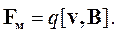
| (1.3) |
Так как вектор напряженности электрического поля воздействует на любой заряд, электрическое поле можно использовать для ускорения потока электронов и для изменения траектории его движения. Оба этих эффекта используются в осциллографических электронно-лучевых трубках.
Взаимодействие магнитного поля с потоком движущихся электронов описывается векторным произведением. Значит, сила действия магнитного поля направлена перпендикулярно траектории движения электронов. Поэтому магнитное поле может только изменять направление движения заряженных частиц - сфокусировать поток электронов или отклонять его. Оба эти эффекта используются в кинескопах.
Для описания процессов в вакууме знания напряженности электрического поля и магнитной индукции достаточно. Однако для правильного описания электромагнитного поля в материальных средах требуется ввести в рассмотрение параметры этих сред.
1.2. Электромагнитное поле в материальных средах
Среды, в которых существует электромагнитное поле, условно, для удобства описания их свойств, делят на три группы – диэлектрики, магнетики и проводники.
1.2.1. Поляризация диэлектриков
Основное свойство диэлектриков, определившее их название, состоит в том, что они не проводят электрический ток. Кроме того, при попадании в электрическое поле диэлектрики поляризуются. По состоянию до попадания в электрическое поле диэлектрики подразделяются на две группы - неполярные и полярные.
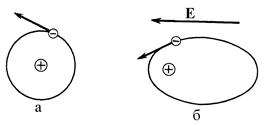
Под действием электрического поля молекулы неполярных диэлектриков превращаются в электрические диполи. Это преобразование иллюстрирует рис. 1.1. Атом любого вещества представляет собой электрически нейтральное объединение заряженных частиц. Положительные заряды сосредоточены в ядре, а отрицательные – в электронной оболочке. Простейший атом водорода имеет в оболочке один электрон. В исходном состоянии (рис. 1.1, а) центр распределенного по электронной оболочке отрицательного заряда совпадает с центром положительного заряда ядра, и атом является электрически нейтральным.
|
| Рис. 1.1. Поляризация атома водорода |
|
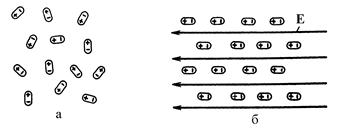
| Рис. 1.2. Поляризация полярных диэлектриков |
Под действием внешнего электрического поля электронная оболочка атома деформируется (рис. 1.1, б). Орбита электрона вытягивается. Ее геометрический центр смещается относительно ядра. В результате атом превращается в электрический диполь. Это явление носит название электронной поляризации вещества.
Молекулы полярных диэлектриков всегда имеют дипольные свойства. В отсутствие внешнего электрического поля молекулярные диполи ориентированы в пространстве хаотически (рис. 1.2, а). Из-за этого их суммарное электрическое поле можно считать равным нулю.
Под действием внешнего электрического поля происходит упорядочение ориентации молекулярных диполей. Очевидно, что степень изменения ориентации диполей будет возрастать с увеличением напряженности электрического поля и падать при увеличении температуры.
Механизм действия величины напряженности электрического поля очевиден – чем она большего, тем выше степень упорядоченности положения молекулярных диполей. Но имеется предел, который наступит тогда, когда все элементарные диполи расположатся вдоль силовых линий электрического поля (рис. 1.2, б). Дальнейшее увеличение напряженности не приведет к увеличению дипольного момента.
Влияние температуры обусловлено тем, что хаотическое тепловое движение молекул нарушает их упорядоченное расположение, а скорость и амплитуда этого движения пропорциональны температуре.
Количественной характеристикой поляризации отдельной молекулы является ее дипольный момент:
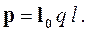
| (1.4) |
| где | l0 | - орт дипольного момента, |
| q | - величина заряда, Кл, | |
| l | - расстояние между зарядами, м |
Так как обычно в единице объема вещества находится много молекулярных диполей, то в качестве меры поляризации диэлектрика вводится вектор поляризации. Он равен произведению количества диполей в единице объема на дипольный момент каждого из них:
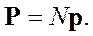
| (1.5) |
| где | N | - количество молекулярных диполей в единице объема вещества. |
Вектор поляризации Ропределяется в каждой точке объема поляризованного диэлектрика. Он зависит от концентрации элементарных диполей и от величины напряженности электрического поля, действующего внутри вещества.
Для описания явлений поляризации диэлектрика вводится вектор электрической индукции D. Его связь с вектором напряженности электрического поля и вектором поляризации описывается формулой:
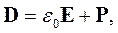
| (1.6) |
| где | ε0 | - электрическая постоянная, Ф/м. |
Электрическая постоянная определена экспериментально и равна 10-9/(36π) Ф/м.
В вакууме, где поляризуемое вещество отсутствует, векторы напряженности поля и индукции связаны соотношением:
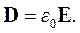
| (1.7) |
Следовательно, электрическая постоянная является коэффициентом пропорциональности между векторами электрической индукции и напряженности электрического поля в вакууме.
Для большинства распространенных сред существует прямо пропорциональная зависимость между вектором напряженности электрического поля и вектором поляризации:
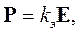
| (1.8) |
где kэ - диэлектрическая восприимчивость вещества.
Таким образом, можно ввести универсальную характеристику диэлектрика - абсолютную диэлектрическую проницаемость:
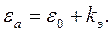
| (1.9) |
Она связывает между собой векторы электрической индукции и напряженности электрического поля в диэлектрике:

| (1.10) |
Абсолютная диэлектрическая проницаемость является коэффициентом пропорциональности между векторами электрической индукции и напряженности электрического поля в веществе.
В практических расчетах часто используется безразмерная характеристика диэлектрика - относительная диэлектрическая проницаемость:
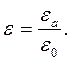
| (1.11) |
Наиболее широко применяемые в радиотехнике диэлектрики имеют относительные диэлектрические проницаемости приблизительно от 2 до 4. Из широко распространенных диэлектриков максимальную относительную диэлектрическую проницаемость, 82, имеет вода.
1.2.2. Намагничивание магнетиков
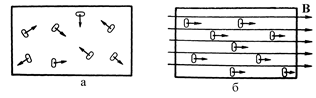
|
| Рис.1.3. Переориентация диполей магнетика под действием внешнего поля |
Магнетиками называют вещества, магнитные свойства которых отличаются от свойств вакуума.
Согласно гипотезе Ампера молекулы магнетиков несут в себе замкнутые токи, то есть являются магнитными диполями. В свободном состоянии молекулярные магнитные диполи ориентированы хаотически, и их суммарным полем можно пренебречь (рис. 1.3, а). Под действием внешнего магнитного поля молекулы магнетика переориентируются, располагаясь вдоль силовых линий магнитного поля (рис. 1.3, б). Этот процесс аналогичен поляризации полярных диэлектриков.
Определение магнитного момента молекулярного диполя иллюстрирует рис. 1.4. Молекулярный ток I - это электрон, вращающийся вокруг ядра. То есть движущийся заряд, ток проводимости. Можно представить это так, что по проводнику, имеющему форму орбиты электрона, протекает ток. Орбита электрона охватывает площадь ΔS.
Магнитный диполь характеризуется магнитным моментом. Он обозначается буквой m и описывается следующим соотношением:
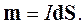
| (1.12) |
| где | m | - вектор магнитного момента, А*м2, |
| I | - молекулярный ток, А, | |
| dS | - векторный дифференциал площади орбиты электрона: dS = dSn0, м2, | |
| n0 | - орт векторного дифференциала. |
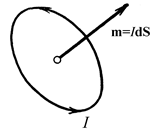
|
| Рис. 1.4. К определению магнитного момента |
Орт векторного дифференциала площади орбиты электрона направлен так, чтобы с его конца движение тока представлялось происходящим против часовой стрелки.
В единице объема магнетика находится много молекулярных токов, поэтому вводится вектор намагниченности. Он описывается формулой:
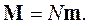
| (1.13) |
| где | N | - количество молекулярных диполей в единице объема вещества. |
Следовательно, можно провести аналогию в поведении полярных диэлектриков в электрическом поле и магнетиков в магнитном поле. В частности, у большинства магнетиков в не слишком сильных магнитных полях связь между векторами магнитного момента и напряженности магнитного поля линейная:
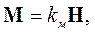
| (1.14) |
где kм - магнитная восприимчивость вещества.
Значит, можно записать формулу, связывающую векторы магнитной индукции и напряженности магнитного поля с учетом процесса намагничивания:
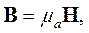
| (1.15) |
где μa - абсолютная магнитная проницаемость вещества.
Абсолютная магнитная проницаемость вещества является коэффициентом пропорциональности между векторами магнитной индукции и напряженности магнитного поля.
В вакууме векторы магнитной индукции и напряженности магнитного поля связаны следующим соотношением:

| (1.16) |
| где | μ0 | - магнитная постоянная, Г/м |
Магнитная постоянная определена экспериментально и равна 4π*10-7 Гн/м.
Магнитная постоянная является коэффициентом пропорциональности между векторами магнитной индукции и напряженности магнитного поля в вакууме.
По аналогии с диэлектриком можно ввести относительную магнитную проницаемость, определив ее следующим соотношением:

| (1.17) |
В отличие от относительной диэлектрической проницаемости, которая в обычных условиях больше единицы, относительная магнитная проницаемость может быть и меньше единицы. Такие вещества называют диамагнетиками.
Если относительная магнитная проницаемость равна единице, это вакуум или иной немагнитный материал.
Если же относительная магнитная проницаемость вещества больше единицы, то оно относится к парамагнетикам. В особый класс выделяют ферромагнетики, у которых относительная магнитная проницаемость значительно больше единицы.
Соотношения (1.10) и (1.15) относятся к материальным уравнениям электромагнитного поля. Материальные уравнения описывают макроскопические свойства вещества, существенные при воздействии на него электромагнитного поля.
Записанные материальные уравнения являются линейными. Линейными являются многие среды, в которых решаются прикладные радиотехнические задачи. Однако существуют и нелинейные среды. К ним относится трансформаторное железо в сравнительно сильном магнитном поле. Из диэлектриков нелинейные свойства при обычных условиях наблюдаются у сегнетоэлектриков, к которым относится, в частности, конденсаторная керамика титанат бария.
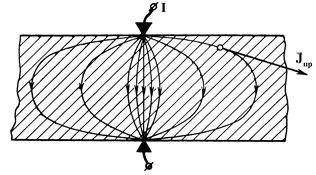
|
| Рис. 1.5. К определению вектора плотности тока проводимости |
Существуют также среды, в которых векторы индукции и напряженности поля не коллинеарны. При этом любая составляющая вектора индукции записывается в виде линейной комбинации всех трех составляющих вектора напряженности поля. Такие среды называют анизотропными. Их проницаемости описываются тензорами.
1.3. Ток проводимости и ток смещения
Током проводимости называется движение носителей электрических зарядов под действием электрического поля.
Для выяснения особенностей протекания тока проводимости в объемных телах рассмотрим проводящее тело в виде бесконечного слоя (рис. 1.5). К этому телу подведены два точечных электрода, соединенные с источником. Ток внутри вещества сконцентрируется вблизи кратчайшего расстояния между электродами, однако меньшая его часть ответвится в глубь тела.
Для описания состояния такой системы необходимо знать скорость и направление движения носителей заряда в каждой точке области протекания тока внутри тела. Для этого вводится понятие плотности тока проводимости. Вектор плотности тока проводимости описывается следующим образом:
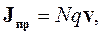
| (1.18) |
| где | 
| - количество носителей заряда в единице объема вещества; |
| q | - заряд носителя, Кл; | |
| v | - вектор скорости движения носителей заряда, м/с. |
Плотность тока проводимости является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости движения носителей. Скорость носителей и плотность тока проводимости пропорциональны напряженности электрического поля:

| (1.19) |
| где | σ | - электропроводность среды, См/м. |
Электропроводность является коэффициентом пропорциональности между векторами плотности тока проводимости и напряженности электрического поля.
Формула (1.19) также относится к материальным уравнениям и называется законом Ома в дифференциальной форме.
Лучшими проводниками являются металлы. Максимальную электропроводность имеет серебро - 6.1*107 См/м. У меди она равна 5.7*107 См/м, а у алюминия - 3.2*107 См/м.
Если мы имеем дело с электрическим полем, постоянным во времени, тока проводимости достаточно. Однако в переменном поле только он не позволяет описать всю совокупность наблюдаемых явлений.
Рассмотрим цепь переменного тока с конденсатором. Переменный ток протекает между обкладками конденсатора и в том случае, когда между ними вакуум, то есть образование тока проводимости невозможно. Соединительный провод, по которому течет ток проводимости, окружен кольцевыми линиями магнитного поля, которые как бы образуют «оболочку» вокруг него. Максвелл предположил, что эта «оболочка» не обрывается у пластин конденсатора. Значит, переменное электрическое поле, так же как и ток проводимости, сопровождается появлением магнитного поля. Это дало Максвеллу основание для введения понятия тока смещения. Плотность тока смещения описывается формулой:
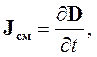
| (1.20) |
Природу тока смещения можно определить следующим образом. Всякое изменение электрического поля приводит к возникновению тока смещения.
Величина тока смещения прямо пропорциональна скорости изменения электрического поля.
| <== предыдущая страница | | | следующая страница ==> |
| Форма внутренней описи документов дела | | | ОСНОВНЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ |
Дата добавления: 2014-11-08; просмотров: 635; Нарушение авторских прав

Мы поможем в написании ваших работ!