
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОСНОВНЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ
2.1. Первое уравнение Максвелла
Первое уравнение Максвелла является обобщением открытого Ампером закона полного тока. Ампер сформулировал этот закон следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна току, пронизывающему контур:
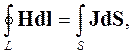
| (2.1) |
| где | L – замкнутый контур, |
| dl – векторный дифференциал длины контура: dl = l0dl, | |
| l0 –орт дифференциала длины контура, | |
| J – вектор плотности тока, пронизывающего контур, | |
| S - произвольная поверхность, опирающаяся на контур L, | |
| dS - векторный дифференциал поверхности:dS = n0dS, | |
| n0 - орт нормали к поверхности S, образующий с направлением обхода контура правовинтовую систему. |
Форма замкнутого контура L может быть произвольной.
Под током, пронизывающим контур, Ампер понимал только ток проводимости, что справедливо для постоянного во времени поля. В переменном поле необходимо учесть введенный Максвеллом ток смещения. При этом формула (2.1) примет вид:
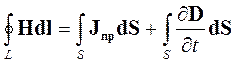
| (2.2) |
Уравнение (2.2) записано для контура конечных размеров и называется первым уравнением Максвелла в интегральной форме.
К дифференциальной форме первого уравнения перейдем с помощью теоремы Стокса (формула (1.34), [6]). Она позволяет заменить циркуляцию вектора Нпо контуруL интегралом от rot Н по поверхности S, опирающейся на этот контур:
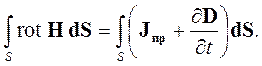
| (2.3) |
Так как поверхность S выбрана произвольно, то равенство (2.3) может быть удовлетворено только в случае равенства подынтегральных выражений:
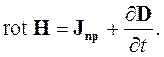
| (2.4) |
Равенство (2.4) называется первым уравнением Максвелла в дифференциальной форме. Этовекторное уравнение эквивалентно трем скалярным уравнениям. В декартовой системе координат х, у, zони примут следующий вид:
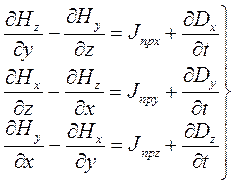
| (2.5) |
Аналогичные уравнения в других системах координат могут быть получены с помощью формул перехода (2.5) – (2.7) или (2.11) – (2.13) [6].
2.2. Второе уравнение Максвелла
Второе уравнение Максвелла базируется на законе электромагнитной индукции Фарадея, который формулируется следующим образом: если замкнутый контур пронизывает переменное магнитное поле, то в контуре возникает электродвижущая сила (ЭДС), равная скорости изменения магнитного потока:
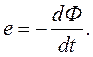
| (2.6) |
Знак минус в правой части формулы означает, что наведенная ЭДС всегда препятствует изменению магнитного потока, пронизывающего контур. Это положение называется правилом Ленца.
Фарадей полагал, что уравнение (2.6) справедливо только в случае контура из проводника. Максвелл предположил, что оно справедливо и в том случае, когда среда не обладает электропроводностью.
Электродвижущая сила, наводимая в любом замкнутом контуре, равна циркуляции вектора напряженности электрического поля по этому контуру:
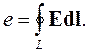
| (2.7) |
| где | L – замкнутый контур, |
| dl – векторный дифференциал длины контура: dl = l0dl, | |
| l0 –орт дифференциала длины контура, |
Магнитный поток, пронизывающий контур, связан с вектором магнитной индукции следующим соотношением
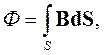
| (2.8) |
| где | S - произвольная поверхность, опирающаяся на контур L, |
| dS - векторный дифференциал поверхности: dS = n0dS, | |
| n0 - орт нормали к поверхности S, образующий с направлением обхода контура правовинтовую систему. |
Подставим формулы (2.7) и (2.8) в (2.6). Получим:
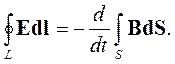
| (2.9) |
Это соотношение записано для контура конечных размеров и называется вторым уравнением Максвелла в интегральной форме. Для перехода к дифференциальной форме уравнения проделаем те же операции, что и в предыдущем параграфе. Получим:
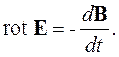
| (2.10) |
Это соотношение называют вторым уравнением Максвелла в дифференциальной форме.
В декартовой системе координат векторное уравнение (2.10) преобразуется в систему из трех скалярных уравнений:
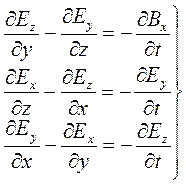
| (2.11) |
Аналогичные уравнения в других системах координат могут быть получены с помощью формул перехода (2.5) – (2.7) или (2.11) – (2.13) [6].
2.3. Третье уравнение Максвелла
Третье уравнение Максвелла базируется на законе Гаусса, который связывает поток вектора электрической индукции через произвольную замкнутую поверхность с зарядом, сосредоточенным внутри этой поверхности:
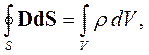
| (2.12) |
| где | S - произвольная замкнутая поверхность, |
| dS - векторный дифференциал поверхности:dS = n0dS, | |
| n0 - орт внешней нормали к поверхности S, | |
| V – объем, ограниченный поверхностью S, | |
| ρ – объемная плотность заряда внутри поверхности S. |
Гаусс получил уравнение (2.12) применительно к постоянным полям. Максвелл предположил, что его можно использовать и в случае переменных полей. Поэтому уравнение (2.12) обычно называют третьим уравнением Максвелла в интегральной форме.
Для перехода к дифференциальной форме надо преобразовать левую часть уравнения (2.12) по теореме Остроградского – Гаусса (формула (1.33) [6]). Получим:
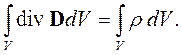
| (2.13) |
Так как никаких ограничений на объем V не наложено, равенство (2.13) выполнится только в том случае, если равны подынтегральные выражения:
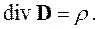
| (2.14) |
Это соотношение называется третьим уравнением Максвелла в дифференциальной форме.
В декартовой системе координат можно от векторного уравнения перейти к скалярному:
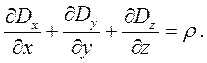
| (2.15) |
Из равенства (2.14) следует, что дивергенция вектора электрической индукции отлична от нуля только в тех точках пространства, где имеются свободные заряды. В этих точках линии вектора D имеют начало (исток) или конец (сток). Линии вектора электрической индукции начинаются на положительных зарядах и заканчиваются на отрицательных.
2.4. Четвертое уравнение Максвелла
Четвертое уравнение Максвелла базируется на законе Гаусса для магнитного поля, который можно сформулировать следующим образом: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
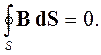
| (2.16) |
Это уравнение означает, что не существует линий вектора магнитной индукции, которые только входят в замкнутую поверхность S или только выходят из нее. Они всегда пронизывают замкнутую поверхность насквозь.
Уравнение (2.16) называют четвертым уравнением Максвелла в интегральной форме.
К дифференциальной форме уравнения можно перейти с помощью теоремы Остроградского-Гаусса так же, как это было сделано в случае третьего уравнения Максвелла. В результате получим:
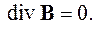
| (2.17) |
Уравнение (2.17) называется четвертым уравнением Максвелла. Оно утверждает факт отсутствия в природе магнитных зарядов. Из этого уравнения следует также, что силовые линии магнитного поля являются непрерывными.
2.5. Уравнение непрерывности
Уравнение непрерывности является математической формулировкой закона сохранения заряда, который утверждает, что ни при каких условиях электрические заряды не могут самопроизвольно зарождаться или бесследно исчезать.
Рассмотрим произвольный замкнутый объем V, ограниченный поверхностью S. Пусть внутри этого объема содержится некоторый заряд Q. Величина этого заряда может быть найдена интегрированием объемной плотности зарядапо всему объему:

| (2.18) |
Предположим, что величина заряда в объеме изменяется. В соответствии с законом сохранения заряда следует считать, что часть зарядов пересекает поверхность S, ограничивающую объем V. При этом возникает ток проводимости с плотностью Jnp.
Проинтегрируем плотность тока проводимости по поверхности, ограничивающей наш объем. Получим:
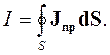
| (2.19) |
По определению ток проводимости - это скорость изменения заряда:
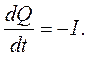
| (2.20) |
Знак минус говорит о том, что ток считается положительным, если величина заряда внутри объема уменьшается. С помощью формул (2.19) и (2.20) легко связать скорость изменения плотности заряда с плотностью тока проводимости:
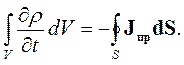
| (2.21) |
Для получения дифференциальной формы закона сохранения заряда преобразуем уравнение аналогично тому, что было сделано в предыдущем параграфе:
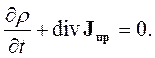
| (2.22) |
Соотношение (2.22) называется уравнением непрерывности.
2.6. Полная система уравнений Максвелла
Каждое из рассмотренных выше уравнений описывает некоторые свойства электромагнитного поля. Однако анализ электромагнитных процессов возможен только на основе решения системы уравнений Максвелла. Большинство задач электродинамики решается с помощью системы уравнений в дифференциальной форме:
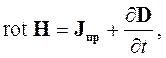
| 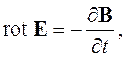
| (2.23) |
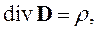
| 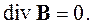
|
Систему (2.23) необходимо решать совместно с материальными уравнениями, связывающими между собой векторы электромагнитного поля. В случае линейных изотропных сред эти уравнения имеют вид:
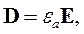
| 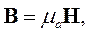
| 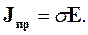
| (2.24) |
Уравнения Максвелла позволяют выделить следующие основные свойства электромагнитного поля:
· электрическое и магнитное поля тесно связаны между собой: любое изменение одного из них вызывает изменение другого;
· источниками электромагнитного поля являются заряды и токи;
· магнитное поле всегда вихревое, электрическое поле может быть вихревым и потенциальным;
· силовые линии электрического поля могут иметь истоки и стоки, силовые линии магнитного поля всегда непрерывны.
Из первого уравнения Максвелла следует, что линии магнитного поля охватывают линии полного тока, образуя с ними правовинтовую систему (рис. 2.3, а). Из второго уравнения Максвелла вытекает, что линии вихревого электрического поля охватывают линии вектора дВ/дt, образуя с ними левовинтовую систему (рис. 2.3, б).

|
| Рис. 2.1. Взаимосвязи электрической и магнитной составляющих переменного электромагнитного поля |
Уравнения Максвелла и материальные уравнения являются линейными дифференциальными уравнениями. Поэтому электромагнитные поля удовлетворяют принципу суперпозиции: поле, созданное несколькими источниками, можно рассматривать как сумму полей созданных каждым источником.
В дополнение к уравнениям Максвелла в дифференциальной форме в ряде случаев необходимо использовать уравнения Максвелла в интегральной форме:
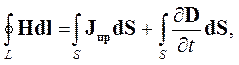
| 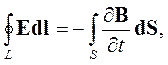
| (2.25) |
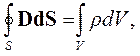
| 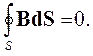
|
2.7. Классификация электромагнитных явлений по зависимости от времени
Система уравнений Максвелла охватывает всю совокупность электромагнитных явлений макроскопической электродинамики. Их решение в общем виде вызывает значительные и, как правило, не преодолимые затруднения. Однако в ряде частных случаев эти уравнения упрощаются.
Самым простым является случай, когда электромагнитное поле не зависит от времени и нет тока проводимости. При этих условиях система уравнений Максвелла распадается на две независимые системы:
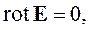
| 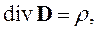
| 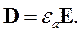
| (2.26) |
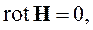
| 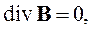
| 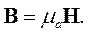
| (2.27) |
Система уравнений (2.26) содержит только электрические величины и описывает электростатическое поле. Система уравнений (2.27) описывает магнитостатическое поле. Это означает, что в рассматриваемом случае электрические и магнитные явления независимы. Электростатические поля создаются неподвижными и неизменными по величине зарядами. Система (2.26) является полной системой дифференциальных уравнений электростатики. Уравнения (2.27) описывают поля постоянных магнитов.
Если среда имеет электропроводность, электрическое и магнитное поле перестают быть независимыми. Такое поле называется стационарным электромагнитным полем. Система уравнений Максвелла в этом случае принимает вид
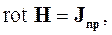
| 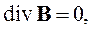
| 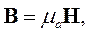
| (а) | (2.28) |
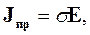
| ||||
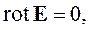
| 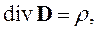
| 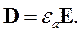
| (б) |
Уравнения (а) описывают магнитное поле, а уравнения (б) – электрическое. Они связанны между собой током проводимости, который вызывается электрическим полем и возбуждает магнитное поле.
Переходным от постоянного во времени к переменному является так называемое квазистационарноеполе. Квазистационарные процессы протекают достаточно медленно, поэтому током смещения в первом уравнении Максвелла можно пренебречь. Это позволяет применить для описания переменного поля соотношения, полученные для поля, не изменяющегося во времени.
Ранее при рассмотрении системы уравнений Максвелла учитывались только токи проводимости и токи смещения, возникающие под действием электрической составляющей электромагнитного поля. При этом полагалось, что источники расположены достаточно далеко и их взаимодействием с полем в интересующей нас области можно пренебречь. Такое поле называется свободным. Задачи для свободного поля решаются проще всего.
Однако, если необходимо рассчитывать процессы возбуждения поля, влиянием источников пренебречь не удается. Поле, возбуждаемое источниками, называется вынужденным. Источники, создающее поле за счет преобразования иной энергии в энергию электромагнитного поля, называются сторонними. При решении задач электродинамики характеристики сторонних источников считаются известными.
Чаще всего влияние сторонних источников задается с помощью сторонних токов. Для их учета первое уравнение Максвелла надо представить в следующем виде:
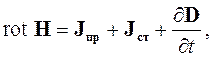
| (2.29) |
где Jст - плотность сторонних токов в рассматриваемой точке пространства.
Кроме того, вместо сторонних токов можно задавать стороннюю напряженностьэлектрического поля Ест. Под Ест обычно подразумевается напряженность электрического поля, создаваемая зарядами и токами, сосредоточенными за пределами рассматриваемой области.
Аналогично сторонним токам вводится понятие сторонних зарядов. Сучетом сторонних зарядов третье уравнение Максвелла записывается в виде
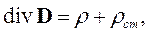
| (2.30) |
где ρст - объемная плотность сторонних зарядов.
3. НЕКОТОРЫЕ ОСОБЕННОСТИ РЕШЕНИЯ УРАВНЕНИЙ ЭЛЕКТРОДИНАМИКИ
3.1. Метод комплексных амплитуд
В систему Максвелла входят уравнения в частных производных. Решение системы уравнений в частных производных тем сложнее, чем больше количество независимых переменных они содержат. В рассматриваемую систему входят частные производные по четырем независимым переменным, х, у, z и t, поэтому для упрощения решения полезно исключить хотя бы одну из них. Это возможно, если электромагнитный процесс является монохроматическим, то есть изменяется во времени по гармоническому закону.
В природе таких процессов нет, так как монохроматический процесс должен существовать всегда и иметь постоянную амплитуду. Такой процесс не является сигналом и с его помощью нельзя передавать информацию. Однако большинство радиосигналов, встречающихся на практике, можно представить как совокупность гармонических составляющих. Чаще всего для такого представления используются ряды или интегралы Фурье.
Суть метода комплексных амплитуд рассмотрим на примере напряженности электрического поля, изменяющейся по гармоническомузакону. Ее изменение во времени можно описать следующим образом:
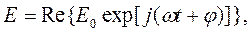
| (3.1) |
| где | Е0 – амплитуда, |
| ω – круговая частота, | |
| φ – фаза. |
Во многих случаях операцию взятия действительной части можно опустить и оперировать с комплексными величинами, которые будем обозначать точкой сверху:
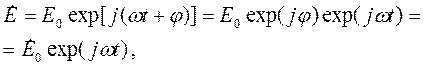
| (3.2) |
| где | 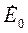 – комплексная амплитуда: – комплексная амплитуда:
|
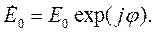
| (3.3) |
Комплексной амплитудой называется часть математического описания гармонического процесса, не зависящая от времени, а проведение расчетов с использованием комплексного представления гармонических величин называется методом комплексных амплитуд.
Возьмем производную по времени от последней формы записи формулы (3.2). Получим:
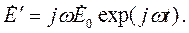
| (3.4) |
Отсюда следует, что операцию дифференцирования по времени можно заменить умножением на jω. Если необходимо вычислить вторую производную, правую часть формулы (3.4) надо умножить на jω еще раз:
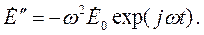
| (3.5) |
И так далее. Значит, дифференцирование по времени свелось к умножению на jω. Очевидно, что это проще и на одну переменную, по которой проходит дифференцирование в уравнениях, стало меньше. Следовательно, упростилось решение системы уравнений Максвелла.
Запишем уравнения Максвелла для комплексных амплитуд:
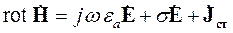 , ,
|  , ,
| (3.6) |
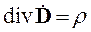 , ,
| 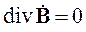 , ,
| |
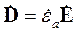 , ,
| 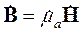 . .
|
Необходимо обратить внимание на то, что абсолютная диэлектрическая проницаемость и абсолютная магнитная проницаемость в материальных уравнениях записаны как комплексные величины. Такое представление упрощает описание распространения электромагнитного поля в среде с электрическими и магнитными потерями.
Электрические потери имеют место быть в среде с отличной от нуля электропроводностью, а магнитные – в магнетике. В подавляющем большинстве случаев имеются только электрические потери, поэтому их и рассмотрим далее.
3.2. Комплексная диэлектрическая проницаемость
Для вывода формулы, описывающей комплексную диэлектрическую проницаемость, воспользуемся материальным уравнением для электрического поля и перепишем первое уравнение системы (3.6) в следующем виде:
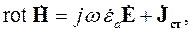
| (3.7) |
| где | 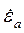 – комплексная диэлектрическая проницаемость: – комплексная диэлектрическая проницаемость:
|
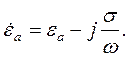
| (3.8) |
Действительная часть комплексной характеристики поля или среды в электродинамике обычно обозначается штрихом вверху, а мнимая – двумя штрихами:
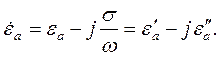
| (3.9) |
Введение комплексной диэлектрической проницаемости позволяет легко учитывать как диэлектрические, так и проводящие свойства вещества. Величина вещественной части абсолютной диэлектрической проницаемости говорит об интенсивности процесса поляризации. Мнимая часть характеризует плотность токов проводимости.
Комплексную абсолютную диэлектрическую проницаемость можно изобразить на комплексной плоскости (рис. 3.1). Она образует с действительной осью отрицательный угол δ, который называется углом диэлектрических потерь.
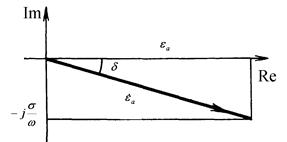
|
| Рис. 3.1. Комплексная диэлектрическая проницаемость на комплексной плоскости |
Величина угла диэлектрических потерь определяется соотношением между мнимой и действительной частями комплексной диэлектрической проницаемости. На практике чаще всего пользуются тангенсом угла диэлектрических потерь:
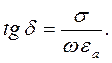
| (3.10) |
Тангенс угла диэлектрических потерь равен отношению плотности токов проводимости и плотности токов смещения. В электродинамике он используется для классификации сред.
Электропроводность природных сред лежит в интервале приблизительно от 10-17 до 6.1*107 См/м. Из-за такой разницы электропроводности сред их поведение в электромагнитном поле будет различным. Чем больше величина электропроводности, тем больше плотность тока проводимости в среде при той же напряженности электрического поля. С другой стороны, чем выше скорость изменения электрического поля и диэлектрическая проницаемость, тем больше плотность тока смещения.
Для упрощения анализа вводятся понятия идеального проводникаи идеального диэлектрика.Идеальный проводник - это среда с бесконечно большой электропроводностью (σ → ∞), а у идеального диэлектрика электропроводности нет (σ = 0). В идеальном проводнике может существовать только ток проводимости, а в идеальном диэлектрике - только ток смещения.
В реальных средах имеется ток проводимости и ток смещения, Поэтому проводниками принято называть среды, в которых ток проводимости намного превосходит ток смещения. Среды, в которых основным является ток смещения, относят к диэлектрикам. Полупроводником считается среда, в которой токи смещения и токи проводимости одного порядка, то есть тангенс угла электрических потерь порядка единицы.
Такое деление сред имеет относительный характер, так как, при прочих равных условиях, зависит от скорости изменения электромагнитного поля, то есть от частоты.
3.3. Перестановочная двойственность уравнений Максвелла
Рассмотрим первое и второе уравнение Максвелла в комплексной форме для свободного поля:
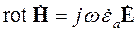 , ,
| (3.11) |
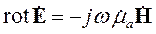 . .
| (3.12) |
Если сравнить эти уравнения между собой, легко обнаружить, что они переходят одно в другое в результате следующих замен:
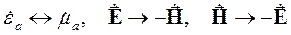
| (3.13) |
Эти соотношения формализует принцип перестановочной двойственности для свободного поля.
Перестановочная двойственность уравнений Максвелла имеет большое практическое значение. Существуют такие электродинамические задачи, в которых векторы напряженности электрического и магнитного полей меняются ролями. Если одна из таких «парных» задач решена то для получения решения второй задачи достаточно в готовых формулах сделать замену, задаваемую условиями (3.13). Решение в этом случае получено путем применения принципа перестановочной двойственности.
Распространим принцип двойственности на уравнения Максвелла с источниками. Для этого запишем первое и второе уравнения:
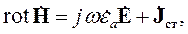
| (3.14) |
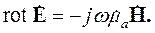
|
Систему (3.14) необходимо дополнить модифицированными уравнениями:
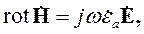
| (3.15) |
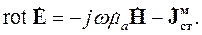
|
| где | 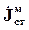 – комплексная амплитуда вектора плотности сторонних магнитных токов. – комплексная амплитуда вектора плотности сторонних магнитных токов.
|
Сопоставим обе системы уравнений. Известная система уравнений (3.14) переходит в модифицированную систему (3.15), если произвести следующие замены:
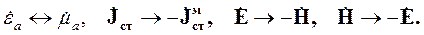 . .
| (3.16) |
Эти соотношения отличаются от аналогичных, имеющих номер (3.13), тем, что в них присутствуют векторы плотности сторонних токов. То есть они относятся к вынужденному полю. Кроме того, в уравнениях (3.15) источники заданы специальным образом. В правой части второго уравнения стоит магнитный аналог вектора плотности сторонних электрических токов. Это комплексная амплитуда вектора плотности сторонних магнитных токов. Однако в природе магнитные заряды отсутствуют. Следовательно, не может быть и магнитных токов. Но это не мешает вводить такие объекты формально для упрощения исследования реальных полей.
Замена (3.16) может производиться и в готовых формулах, описывающих решения задач.
4. ЭНЕРГИЯ И МОЩНОСТЬ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Энергией называется общая количественная мера различных форм движения материи, а мощностью называется работа, производимая в единицу времени.
Электромагнитное поле обладает энергией, значит, ее можно определить. При этом векторы поля и электродинамические характеристики средысчитаем известными.
4.1. Баланс энергии электромагнитного поля
Вначале сформулируем уравнение баланса энергии в общем виде. Для этого рассмотрим объем V, заполненный однородной изотропной средой и ограниченный поверхностью S. Пусть в этом объеме за счет действия сторонних источников выделяется электромагнитная энергия. Очевидно, что мощность, выделяемая сторонними источниками, может расходоваться на потери в среде, на изменение запаса энергии внутри объема и на излучение в окружающую среду через поверхность S. При этом должно выполняться следующее равенство:
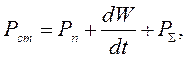
| (4.1) |
| где | Рст - мощность сторонних источников, Вт; |
| Рп - мощность потерь внутри объема V, Вт; | |
| PΣ - мощность, излучаемая через поверхность S, Вт; | |
| W - энергия электромагнитного поля, сосредоточенная в объеме V, Вт*с; | |
| dW/dt - мощность, расходуемая на изменение запаса энергии внутри объема V, Вт. |
Уравнение (4.1) дает качественное представление об энергетических соотношениях в электромагнитном поле. Для определения количественных характеристик воспользуемся уравнениями Максвелла.
Рассмотрим первое уравнение Максвелла с учетом сторонних токов из системы (2.23). Все члены этого уравнения - векторные величины, имеющие размерность ампер на квадратный метр (А/м2). Чтобы сравнить его с уравнением (4.1) нужно преобразовать все слагаемые в скалярные величины, измеряющиеся в ваттах. Для этого достаточно скалярно умножить их на вектор Еипроинтегрировать полученное выражение по объему V. После скалярного умножения получим:
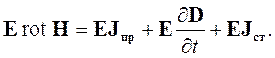
| (4.2) |
Далее необходимо использовать формулу векторного анализа (1.26) [6] и выразить из нее произведение Еrot Н, стоящие в правой части уравнения (4.2):
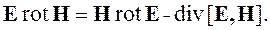
| (4.3) |
Подставим это выражение в формулу (4.2) и перенесем произведение вектора напряженности электрического поля на вектор плотности сторонних токов в левую часть, а все остальные слагаемые – в правую. Кроме того, с помощью второго уравнения Максвелла заменим rot Е на производную по времени от вектора магнитной индукции с обратным знаком и с помощью формул (1.9), (1.14) выразим векторы индукции через соответствующие векторы напряженности поля и проницаемости. Получим:
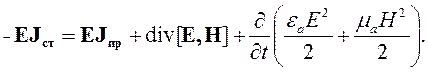
| (4.4) |
Векторное произведение векторов Е и Н обозначается буквой Пи называется вектор Пойнтинга:
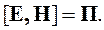
| (4.5) |
Осталось проинтегрировать уравнение (4.4) по объему V. В результате получим:
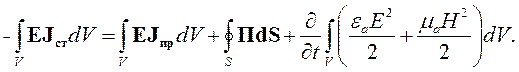
| (4.6) |
В преобразовании уравнения (4.6) использована теорема Остроградского-Гаусса (1.33) [6]. Кроме того, в последнем слагаемом правой части уравнения изменен порядок операций интегрирования и дифференцирования.
Левая часть уравнения (4.6) определяет мощность, отдаваемую сторонними токами в объеме V. Сторонний ток проводимости – это упорядоченное движение заряженных частиц. Для простоты положим, что векторы напряженности электрического поля и плотности сторонних токов коллинеарны. Если частицы тормозятся полем, ток отдает ему свою энергию. Для этого требуется, чтобы векторы напряженности электрического поля и плотности стороннего тока были направлены противоположно. Значит, скалярное произведение векторов Е и Jст будет отрицательным и левая часть уравнения (4.5) станет положительной величиной. Такая ситуация характерна для работы некоторых передающих антенн.
Если векторы плотности стороннего тока и напряженности электрического поля направлены в одну сторону, заряженные частицы будут ускоряться полем, и ток станет отбирать у него энергию. Эту процедуру осуществляют разного рода приемные антенны, однако энергия, которую они могут отнять у поля в свободном пространстве, невелика.
Иначе обстоит дело в волноводах, которые служат для передачи энергии от источника к потребителю. На входном конце волновода сторонние силы реализуют процедуру возбуждения поля. Когда энергия достигает конца волновода, ее надо полностью отобрать у поля и передать потребителю. Для этого используются приемные устройства, преобразующие энергию электрической или магнитной составляющей поля в ток проводимости и передающие его дальше. В этом случае требуется отбирать у поля максимум энергии.
Реальная среда всегда обладает электропроводностью. Поэтому, зная напряженность электрического поля и электропроводность среды, можно найти мощность тепловых потерь, т. е. энергию, теряемую электромагнитным процессом за единицу времени.
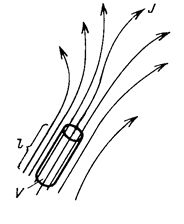
|
| Рис. 4.1. К определению мощности потерь |
Электрическая мощность – это произведение тока на напряжение. Нам известна напряженность электрического поля и электропроводность среды. Значит, можно определить плотность тока проводимости, создаваемого полем. Напряженность электрического поля имеет размерность В/м, а плотность тока проводимости – А/м2. Их произведение будет иметь размерность Вт/м3, то есть плотности мощности. Значит, первое слагаемое в правой части формулы (4.6), интеграл от плотности мощности, описывает мощность потерь.
Обратимся к рис. 4.1, на котором изображена картина линий вектора плотности тока проводимости. В объеме протекания тока выделена цилиндрическая область V. Этот цилиндр имеет длину l и площадь основания S, а ось его совпадает с направлением вектора плотности тока проводимости. Для упрощения решения задачи область должна быть так мала, чтобы вектор плотности тока внутри нее можно было бы считать не зависящим от координат. В этом случае в соответствии с первым слагаемым правой части формулы (4.6) получим:
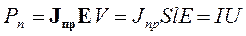
| (4.7) |
Так как плотность тока проводимости и напряженность поля не зависят от координат, они вынесены из-под знака интеграла. Там остался только скалярный дифференциал объема. Его интегрирование по объему дает величину объема. В средней части формулы (4.7) объем цилиндра представлен как произведение площади его основания S на длину l, а параллельные векторы плотности тока и напряженности поля заменены их модулями. Ток I в последней части формулы определен как произведение площади основания цилиндра на плотность тока, а напряжение U – как произведение длины цилиндра на напряженность электрического поля.
Равенство (4.7) эквивалентно закону Джоуля - Ленца.
Для выяснения физического смысла последнего слагаемого в правой части уравнения (4.6) рассмотрим частный случай. Предположим, что объем V окружен идеальной проводящей оболочкой, совпадающей с поверхностью S. Такая оболочка блокирует обмен энергией с внешней средой, и объем становится энергетически изолированным. В этом случае тангенциальная (касательная) составляющая напряженности электрического поля на поверхности S будет равна нулю. Векторный дифференциал поверхности dS совпадает по направлению с ортом внешней нормали n0. Следовательно, поверхностный интеграл в уравнении (4.6) будет равен нулю из-за того, что нормальная компонента векторного произведения [Е, Н]определяется тангенциальными составляющими входящих в него векторов.
Предположим, кроме того, что электропроводность среды в объеме V равна нулю. Значит, тепловые потери исчезнут, и первый интеграл в правой части уравнения (4.6) также будет равен нулю. Получим:
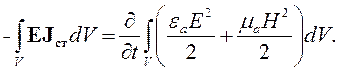
| (4.8) |
В таком изолированном объеме без потерь мощность сторонних источников может расходоваться только на изменение запаса энергии электромагнитного поля. Значит, правая часть уравнения (4.8) равна скорости изменения энергии электромагнитного поля, запасенной в объеме V, а интеграл в правой части этого уравнения равен энергии электромагнитного поля в объеме V:
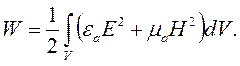
| (4.9) |
Осталось выяснить физическую сущность поверхностного интеграла в уравнении (4.6). Предположим, что потери внутри объема V отсутствуют и, кроме того, величина электромагнитной энергии остаетсяпостоянной. B этом случае уравнение (4.6) примет следующий вид:
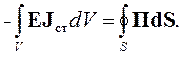
| (4.10) |
Потерь в объеме нет, и запас энергии не меняется, значит, вся мощность сторонних источников должна излучаться в окружающее пространство. Следовательно, поток вектора Пойнтинга П через поверхность S равен излучаемой мощности, которую в уравнении (4.1) мы обозначили РΣ.
Таким образом, качественное уравнение (4.1) преобразовано в уравнение (4.6) с помощью которого можно проводить количественные оценки составляющих баланса мощности.
Рассмотрим частный случай отбора энергии электромагнитного поля сторонними источниками. Пусть энергия поступает в объем V из окружающего пространства. Часть ее преобразуется в тепло, а другая отбирается сторонними источниками. При этом количество электромагнитной энергии, запасенной в объеме V, не изменяется. Уравнение (4.6) в этом случае надо переписать в следующем виде:
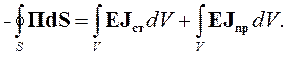
| (4.11) |
Левая часть уравнения (4.11) определяет мощность, поступающую в объем V извне, а правая часть - мощность, расходуемую в этом объеме. Это уравнение было получено Пойнтингом и носит название теоремы Пойнтинга в интегральной форме.
Так как левая часть уравнения (4.11) представляет собой поток энергии, то вектор Пойнтинга является вектором плотности потока энергии. Направление вектора Пойнтинга в изотропной среде совпадает с направлением распространения энергии.
4.2. Плотность энергии электромагнитного поля
Мы выяснили, что энергия, запасенная электромагнитным полем в объеме V определяется формулой (4.9). Интеграл в этом выражении можно представить в виде суммы двух слагаемых, одно из которых зависит только от электрического поля, а второе - только от магнитного:
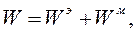
| (4.12) |
где Wэ – энергия электрического поля, Вт*с:
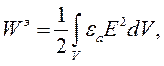
| (4.13) |
Wм - энергия магнитного поля, Вт*с:
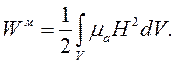
| (4.14) |
Подынтегральные выражения в формулах (4.13) и (4.14) описывают объемные плотности энергии электрического и магнитного полей:
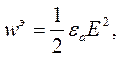
| (4.15) |
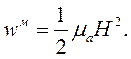
| (4.16) |
Сумма результатов вычислений по формулам (4.15) и (4.16) дает объемную плотность полной энергии электромагнитного поля.
Необходимо обратить внимание на следующий факт. Векторы напряженности электрического и магнитного полей удовлетворяют принципу суперпозиции. Это означает, что векторы напряженности полей, созданных разными источниками, складываются. Однако этот принцип не распространяется на энергию.
Для доказательства этого рассмотрим два поля, вектора напряженности которых равны Е1, Н1 и Е2, Н2 соответственно. Они существуют в одной области V и имеют энергии W1 и W2. Векторы напряженности суммарного поля определятся простым суммированием: Е = Е1 + Е2, Н = Н1 + H2. Энергию суммарного поля надо определять по формуле (4.9):
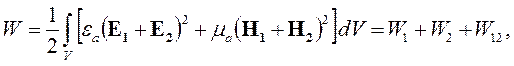
| (4.17) |
где W12 - взаимная энергия полей:
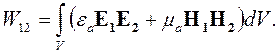
| (4.18) |
Взаимная энергия может быть как положительной, так и отрицательной. Если же векторы Е1 и Е2, а также Н1 и Н2 взаимно перпендикулярны, то взаимная энергия полей равна нулю.
В переменном электромагнитном поле энергия непрерывно перераспределяется между электрическим и магнитным полем. Это перераспределение в каждой точке поля описывается уравнением (4.4). Однако его целесообразно переписать в ином виде:
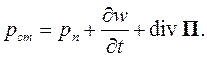
| (4.19) |
| где | рст = -EJст - плотность мощности сторонних источников, Вт/м3; |
| pп = EJп - плотность мощности тепловых потерь, Вт/м3; |
Уравнение (4.19) является дифференциальной формой теоремы Пойнтинга.
4.3. Скорость распространения электромагнитной энергии
Электромагнитная энергия распространяется в пространстве не мгновенно, а с некоторой скоростью. Для определения этой скорости в пространстве, в котором распространяется энергия, выделим энергетическую трубку (рис. 4.2). Форма трубки должна быть такой, чтобы ее боковая поверхность совпадала с направлением вектора Пойнтинга. То есть на боковой поверхности трубки нормальная составляющая вектора Пойнтинга должна быть равна нулю.
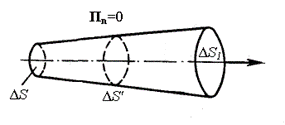
|
| Рис. 4.2. Энергетическая трубка |
За время Δt через поперечное сечение трубки ΔS проходит энергия ΔW. Она сосредоточена в объеме ΔV между сечениями трубки ΔS и ΔS1. Расстояние между этими сечениями равно Δl. При этих условиях скорость распространения энергии можно описать формулой:
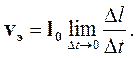
| (4.20) |
| где | vэ – скорость распространения энергии, м/с; |
| 10 - орт, показывающий направление распространения энергии |
Энергию ΔW, распространяющуюся вдоль трубки, можно определить интегрированием плотности энергии по площади сечения трубки и умножением результата на ее длину:
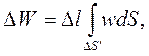
| (4.21) |
| где | ΔS' - поперечное сечение трубки, расположенное между ΔS и ΔS1 |
Положение этого сечения не важно, так как через любое сечение трубки за время Δt проходит вся энергия ΔW. При достаточно малых промежутках времени Δt вектор Пойнтинга можно считать неизменным, поэтому, кроме равенства (4.21) должно выполняться еще одно:
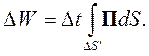
| (4.22) |
Для того чтобы определить скорость переноса энергии надо разделить Δl на Δt и устремить Δt к нулю. Для этого надо формулу (4.22) разделить на формулу (4.21), выделить искомое отношение и выполнить предельный переход:
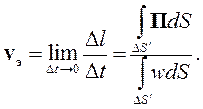
| (4.23) |
Если векторы Е и Нпостоянны в сечении ΔS, постоянными будут и вектор Пойнтинга П и объемная плотность энергии w.В этом случае соотношение (4.23) можно упростить, основываясь на том, что направление вектора Пойнтинга совпадает с направлением распространения энергии:
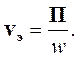
| (4.24) |
Следовательно, скорость переноса энергии электромагнитным полем можно вычислить, разделив плотность потока энергии (вектор Пойнтинга) на плотность энергии.
4.4. Баланс энергии при гармонических колебаниях
В радиотехнике гармонические колебания электромагнитных полей обычно бывают высокочастотными. Поэтому их энергетические характеристики чаще всего целесообразно усреднять по времени. Правила усреднения комплексных амплитуд описаны во многих учебниках и приведены, в том числе, в [6].
Результат усреднения можно выразить через комплексные амплитуды. Например, плотности энергии электрического и магнитного полей в формулах (4.15) и (4.16) пропорциональны квадратам напряженностей. С использованием комплексных амплитуд среднюю плотность энергии, запасенной электромагнитным полем, можно описать формулой:
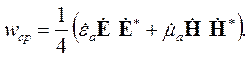
| (4.25) |
Среднее значение плотности мощности определяется как действительная часть комплексной плотности мощности:
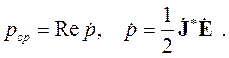
| (4.26) |
| где | 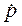 -плотность комплексной мощности, Вт/м3 -плотность комплексной мощности, Вт/м3
|
Аналогично определяется среднее значение вектора Пойнтинга:
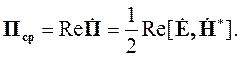
| (4.27) |
Для того чтобы понять, как соотносятся мгновенные и средние значения энергетических величин, проанализируем формулу (4.26), описывающую плотность мощности. Пусть имеется электрическая составляющая электромагнитного поля, которая описывается следующей формулой:
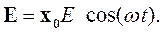
| (4.28) |
В том же объеме существует ток, сдвинутый по фазе относительно напряженности:
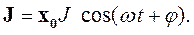
| (4.29) |
| где | φ – угол сдвига фаз между током и напряжением |
При этих условиях плотность мощности можно вычислить по следующей формуле:
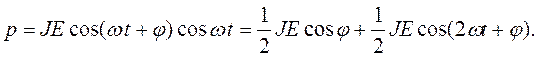
| (4.30) |
Важной особенностью полученного результата является наличие в описании плотности мощности двух слагаемых, изменяющихся по разным законам. Первое слагаемое, пропорциональное cos φ, не зависит от времени и равно среднему значению плотности мощности. Второе слагаемое – переменная составляющая плотности мощности, колеблющаяся с удвоенной частотой.
Результаты расчетов по формуле (4.30) при разных сдвигах фаз между током и напряжением приведены на рис. 4.3. Там построены графики зависимости напряженности электрического поля, плотности тока, мгновенной и средней плотности мощности от времени. Если напряженность поля и ток синфазны, то плотность мощности положительна, а ее среднее значение равно половине максимального (рис. 4.3,а).
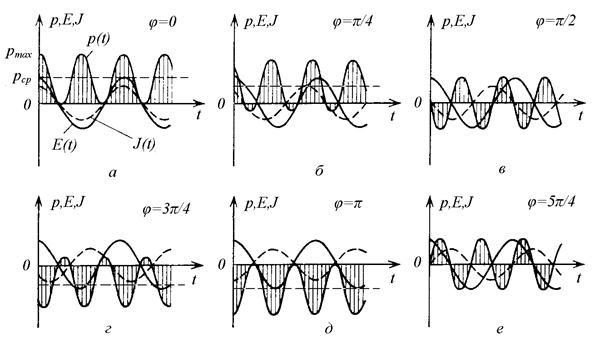
|
| Рис. 4.3. Мгновенные и средние величины плотности мощности |
При сдвиге фаз между током и напряжением π/4 (рис. 4.3, б) мгновенная плотность мощности некоторую часть периода отрицательна. Среднее значение мощности уменьшилось, но осталось положительным. Переменная составляющая мощности превышает среднюю более чем вдвое. При сдвиге фазы π/2 (рис. 4.3, в)среднее значение мощности равно нулю.
Если сдвиг фаз будет расти и дальше, картина изменения средней мощности повторится с изменением знака (рис. 4.3, г – е). Следовательно, переменная составляющая плотности мощности может как угодно превосходить модуль ее среднего значения. Но модуль среднего значения плотности мощности может достигать лишь половины амплитуды переменной составляющей.
Для описания среднего баланса энергии гармонического электромагнитного поля в некоторой области V воспользуемся комплексными амплитудами и комплексными проницаемостями. Прилучим:
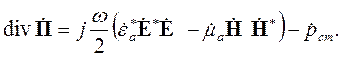
| (4.31) |
В этой формуле за излучение отвечает левая часть, задана плотность комплексной мощности источников (последнее слагаемое в правой части), а электрические и магнитные потери учтены в соответствующих комплексных проницаемостях. Подставим в эту формулу комплексные проницаемости в виде сумм действительной и мнимой частей, выделим действительную и мнимую части результата и проинтегрируем полученные равенства по объему V с границей S. Получим:
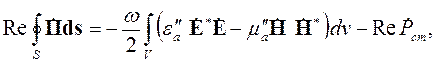
| (4.32) |
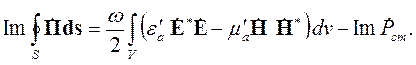
| (4.33) |
| где | 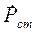 -комплексная мощность источников, Вт. -комплексная мощность источников, Вт.
|
В левой части равенства (4.32) стоит действительная составляющая комплексного потока энергии РΣ – то есть средний поток энергии через поверхность S. Последний член справа дает среднюю мощность источников. Поэтому равенство (4.32) удобно записать в следующем виде:
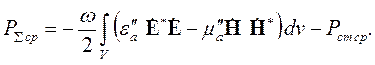
| (4.34) |
Это - уравнение среднего баланса энергиипри гармонических колебаниях.
Пусть источники отдают энергию полю, то есть средняя мощность сторонних источников меньше нуля. Если диэлектрическая и магнитная проницаемости вещественны, то объемный интеграл в формуле (4.32) исчезает. При этом в среднем вся мощность источников будет расходоваться на излучение.
Если же есть потери, то мнимые части проницаемостей будут больше нуля и объемный интеграл в формуле (4.34) будет положительным. Значит, средняя мощность излучения уменьшится на его величину. Из этих рассуждений следует, что объемный интеграл в формуле (4.34), взятый без знака минус, описывает среднюю мощность потерь в объеме V:
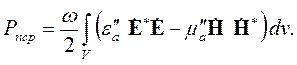
| (4.35) |
Полученный результат еще раз поясняет смысл мнимых частей комплексных проницаемостей. Если они равны нулю, среда не поглощает энергии. Потери энергии существуют, если мнимые части проницаемостей больше нуля. Эти потери происходят в результате преобразования энергии поля в какие-то иные формы, и, в конечном счете – в тепло.
В простейшем варианте поглощение вызывается только электропроводностью среды. Этот случай встречается в практических задачах чаще всего. Для среды без магнитных потерь равенство (4.35) можно переписать в следующем виде:
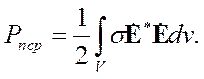
| (4.36) |
Действительная часть мощности сторонних источников называется активной мощностью, а действительная часть мощности излучения - активным потоком энергии. Мнимые части этих величин называются реактивной мощностью и реактивным потоком энергии. При вещественных диэлектрической и магнитной проницаемостях получаем:
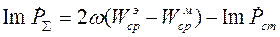
| (4.37) |
Отсюда следует, что реактивные составляющие связаны здесь с разностью средних значений электрической и магнитной энергии в объеме V.
5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ ВТОРОГО ПОРЯДКА И ИХ РЕШЕНИЕ
В основе макроскопической электродинамики лежит полная система уравнений Максвелла. Однако непосредственно решать ее, как правило, трудно. Поэтому необходимо свести уравнения Максвелла к уравнениям математической физики, решения которых известны.
Предположим, что во всем пространстве или в какой-либо энергетически изолированной области сторонний ток отсутствует. Если при этом найдено физически осмысленное решение системы уравнений, то оно описывает свободное электромагнитное поле. Под действием сторонних сил происходит возбуждение электромагнитного поля источниками. Такое поле называется вынужденным или полем излучения. И свободное поле, и поле излучения описываются дифференциальными уравнениями второго порядка в частных производных.
5.1. Дифференциальные уравнения второго порядка в частных производных.
Задачи без источников решать проще. Однако все электромагнитные поля, с которыми практически приходится иметь дело, являются вынужденными. Но если источники находятся достаточно далеко, их взаимодействием с полем в рассматриваемой области можно пренебречь и считать поле свободным. Поэтому решения для свободного поля также интересны.
Для получения уравнений второго порядка из системы уравнений Максвелла нужно исключить все неизвестные величины кроме напряженностей поля. А затем исключить один из векторов, Е или Н. Получим:
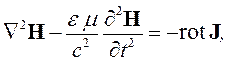
| (5.1) |
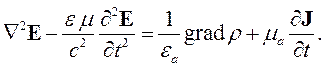
| (5.2) |
| где | с – скорость света в вакууме: |
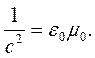
| (5.3) |
Если токи и заряды отсутствуют, уравнения (5.1) и (5.2) утрачивают правые части. Такие однородные уравнения называют волновыми.
Комплексные аналоги этих уравнений второго порядка можно было бы получить, отталкиваясь от уравнений Максвелла в комплексной форме. Но проще добиться желаемого результата, если учесть, что использование метода комплексных амплитуд сводится к следующим заменам:
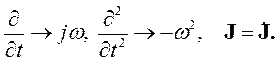
| (5.4) |
В общем случае и проницаемости надо считать комплексными. Сделаем замены в уравнениях (5.1) и (5.2). При этом для преобразования правой части уравнения (5.2) привлечем также закон сохранения заряда в следующем виде:
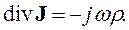
| (5.5) |
Получим:
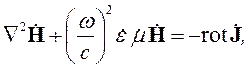
| (5.6) |
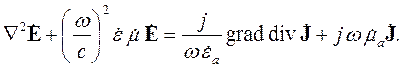
| (5.7) |
Таким образом, мы получили уравнения, позволяющие анализировать характеристики электромагнитного поля. Если к ним добавить граничные условия, можно математически сформулировать подавляющее большинство задач электродинамики.
5.2. Решения волновых уравнений в декартовых, цилиндрических и сферических координатах
Электромагнитное поле, возникающее в некоторой области пространства, не заполняет его мгновенно, а распространяется с конечной скоростью, зависящей от свойств среды. При распространении периодического процесса с конечной скоростью происходит запаздывание его по фазе. Следствием этого является волновой характер распространения электромагнитного поля.
С целью установления волнового характера электромагнитного поля рассмотрим гармонический во времени процесс в области, не содержащей источников. Кроме того, положим, что среда является идеальным диэлектриком. Для того чтобы учесть эти условия, вектор плотности сторонни
| <== предыдущая страница | | | следующая страница ==> |
| ОПИСАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ | | | РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ «Гигиенические основы физкультурно-спортивной деятельности» |
Дата добавления: 2014-11-08; просмотров: 872; Нарушение авторских прав

Мы поможем в написании ваших работ!