Прямые методы решения СЛАУ

Прямым методом решения линейной системы Ах=В называется любой метод, который позволяет получить решение х с помощью заранее известного конечного числа элементарных арифметических операций: сложения, вычитания, деления, умножения и, возможно, извлечения квадратного корня.

Запишем систему линейных алгебраических уравнений (1.11) в развернутом виде

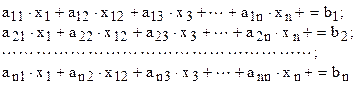(1.12)

Необходимым и достаточным условием существования единственного решения такой системы является неравенство нулю ее определителя.

Наиболее распространенным из прямых методов решения таких уравнений является метод Гаусса и его модификации.

Метод исключения Гаусса.

Как и многие другие, этот метод основан на приведении исходной системы к "треугольному" виду путем последовательного исключения неизвестных во входящих в эту систему уравнениях. Процесс исключения начинается с того, что все члены первого уравнения делят на а₁₁(эта процедура называется нормированием уравнения). Затем первое уравнение последовательно умножается на первые коэффициенты остальных уравнений системы, т. е. на коэффициенты а_i1, и вычитается из каждого из этих (соответствующих) уравнений. По окончании этого процесса первая переменная (х₁) будет исключена из всех уравнений, кроме первого уравнения.

Далее описанная процедура повторяется для остальных n-1 уравнений, т. е. для всех оставшихся, кроме первого, после чего в оставшихся уравнениях окажется исключенной вторая переменная (х₂) и т. д. Описанные действия повторяются до тех пор, пока после преобразований в последнем уравнении системы не останется одна переменная (x_n).

Последнее уравнение системы, содержащее одно неизвестное, позволяет вычислить х_n. После этого, последовательно подставляя значения переменных в вышестоящие уравнения, вычисляют остальные неизвестные x_n-1, x_n-2, …, x₂, x₁, Выполняя описанные выше преобразования исходной системы уравнений, необходимо иметь в виду, что коэффициенты всех нижестоящих уравнений изменяются на каждом шаге.

Точность результатов будет определяться точностью выполнения арифметических операций при преобразовании элементов матрицы. Для уменьшения погрешности при делении на диагональный элемент рекомендуется осуществить такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемой строки. Такая процедура называется выбором главного элемента, а метод называется – метод Гаусса с главным (ведущим) элементом.

Количество арифметических операций в методе Гаусса связано с размерностью системы и примерно равно 2/3 п³.

Используя рассмотренный метод Гаусса, следует учитывать, что коэффициенты матрицы и правой части системы линейных уравнений редко бывают известны точно. Кроме того, СЛАУ часто формируются по результатам эксперимента и тогда ее коэффициенты подвержены ошибкам наблюдения. В некоторых задачах коэффициенты СЛАУ описываются формулами, что влечет ошибки округлений при их вы­числении. Более того, даже если систему можно точно записать в память машины, в ходе ее решения почти неизбежно будут сделаны ошибки округлений. Причем можно показать, что ошибки округлений в гауссовом исключении имеют то же влияние на ответ, что и ошибки в исходных коэффициентах.

Важной характеристикой метода решения является его чувствительность к переносу ошибок округления, или вычислительная устойчивость.

Для оценки чувствительности решения к изменениям значений коэффициентов матрицы в математике используют понятие степень (число) обусловленности матрицы. В практических расчетах оценить обусловленность матрицы можно сравнением решений при вариации коэффициентов матрицы. Матрица считается хорошо обусловленной (решение устойчиво и накопление ошибок незначительно) если малым относительным отклонениям в значениях коэффициентов матрицы соответствует малое относительное изменение решения.

Дата добавления: 2014-10-10; просмотров: 441; Нарушение авторских прав

Мы поможем в написании ваших работ!