
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
СТАТИСТИКА
Пособие
(курс лекций, примеры решения типовых задач,
планы семинарских и практических занятий,
задачи, тесты, вопросы к экзамену) для студентов
экономических специальностей и слушателей
специального факультета по переподготовке кадров
ОСП «Институт повышения квалификации
и переподготовки кадров Белкоопсоюза»
В двух частях
Часть 1
ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
 Гомель 2006
Гомель 2006
УДК 311
ББК 60.60
С 78
Авторы: С. А. Дещеня, канд. экон. наук, первый проректор
Белорусского торгово-экономического университета
потребительской кооперации;
Н. В. Лацкевич, канд. экон. наук, зав. кафедрой;
Л. Н. Пашкова, ст. преподаватель;
Т. Н. Бессонова, ст. преподаватель
Рецензенты: И. И. Колесникова, канд. экон. наук, доцент
кафедры экономики Гомельского государственного
технического университета им. П. О. Сухого;
А. З. Коробкин, канд. экон. наук, доцент,
зав. кафедрой специальных дисциплин
ОСП «Институт повышения квалификации
и переподготовки кадров Белкоопсоюза»
Рекомендовано к изданию научно-методическим советом учреждения образования «Белорусский торгово-экономический университет потребительской кооперации».
Протокол № 5 от 14 июня 2005 г.
| С 78 | Статистика : пособие (курс лекций, примеры решения типовых задач, планы практических занятий, задачи, тесты, вопросы к экзамену) для студентов экономических специальностей и слушателей ОСП «Институт повышения квалификации и переподготовки кадров Белкоопсоюза». В 2 ч. Ч. 1. Общая теория статистики / С. А. Дещеня [и др.]. – Гомель : Учреждение образования «Белорусский торгово-экономический университет потребительской кооперации», 2006. – 180 с. ISBN 985-461-142-6 |
УДК 311
ББК 60.60
| Ó Дещеня С. А. и др., 2006 | |
| ISBN 985-461-142-6 | Ó Учреждение образования «Белорусский торгово-экономический университет потребительской кооперации», 2006 |
ВВЕДЕНИЕ
Знание статистики необходимо специалисту как в области методологии статистического исследования, так и в области анализа основных макроэкономических показателей. Студенты и слушатели, изучающие курс общей теории статистики, овладевают методологией оценки, анализа, моделирования и прогнозирования любых массовых данных об экономических, социальных, природных явлениях и процессах. Кроме того, у них формируется понятие о статистической форме закономерностей сложных систем.
В пособии приведены краткие теоретические сведения по вопросам основных тем курса общей теории статистики, которые составляют методологическую основу статистики. Изложение материала сопровождается пояснениями и расчетами, основанными на фактических и условных цифровых данных.
Пособие включает также планы практических занятий, задачи, тесты, вопросы к экзамену (зачету), глоссарий.
В списке рекомендуемой литературы указаны основные источники, которые необходимо использовать при изучении рассматриваемых вопросов.
Пособие призвано помочь в усвоении курса общей теории статистики.
1. курс лекций, примеры решения
типовых задач
Тема 1. ПРЕДМЕТ, МЕТОД И ЗАДАЧИ СТАТИСТИКИ
Термин «статистика» имеет латинское происхождение (от status – состояние, определенное положение вещей).
Статистический учет существовал уже в глубокой древности, но как наука статистика возникла в XVII в. Первоначально слово «статистика» употреблялось в значении слова «государствоведение», в науку этот термин был введен в 1749 г. немецким ученым Г. Ахенвалем.
У истоков статистической науки стояли две школы:
1. Немецкая описательная, представители которой (Г. Конринг и
Г. Ахенваль) стремились создать теорию и разработать схему описаний государств, систематизировать имеющиеся способы описаний. Однако вести такие описания предлагалось только на момент наблюдения в словесной форме без цифр и вне динамики.
2. Английская школа политических арифметиков, представители которой (Д. Граунт и Э. Петти) стремились изучать явления обще-
ственной жизни с помощью числовых характеристик и способствовали возникновению статистики как теории статистического учета. Они осознавали необходимость учета в статистическом исследовании закона больших чисел, так как только в большом объеме анализируемой совокупности может проявиться закономерность развития, изменения.
В настоящее время под термином «статистика» понимается следующее:
· определенная отрасль практической деятельности (сбор, обработка, анализ различных данных, отражающих разнообразные явления общественной жизни);
· цифровой материал, отражающий состояние различных явлений общественной жизни, конкретных отраслей, организаций и т. п.;
· наука, отрасль знания.
Как всякая наука, статистика имеет свои предмет и метод исследования.
Предметом изучения статистики является количественная сторона массовых общественных явлений в неразрывной связи с их каче-
ственной стороной. Количественное выражение массовых закономерностей общественного развития исследуется статистикой в конкретных условиях (с учетом места и времени).
Метод статистики – это совокупность приемов, используя которые, статистика исследует свой предмет. Можно выделить следующие группы методов:
1. Метод массовых наблюдений (сбор первичного статистического материала).
2. Метод группировок (систематизация и классификация собранного материала).
3. Метод обобщающих показателей (расчет разнообразных показателей, выявляющих взаимосвязи и закономерности развития различных явлений).
Изучает свой предмет статистика при помощи определенных категорий:
· Статистическая совокупность, под которой понимается масса единиц, объединенных единой качественной основой, но отличающихся друг от друга отдельными признаками.
· Единица совокупности, или первичный элемент статистической совокупности, являющийся носителем признаков, подлежащих регистрации.
· Признак, характеризующий качественную особенность единицы совокупности. В статистическом исследовании изучаются признаки, принимающие различные значения или имеющие различные количественные уровни у отдельных единиц совокупности, т. е. варьирующие признаки. Вариация – это изменение величины признака при переходе от одной единицы совокупности к другой.
· Статистический показатель, под которым подразумевается понятие, отражающее количественную характеристику соотношения признаков общественных явлений. Показатели могут быть объемными (численность населения, размер товарооборота) и расчетными (средний размер заработной платы работника, средний размер товарооборота на одного работника), а также плановыми, отчетными (фактическими) и прогнозными.
· Система статистических показателей, т. е. совокупность статистических показателей, отображающая взаимосвязи, которые объективно существуют между явлениями.
Тема 2. СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ
Статистическое наблюдение – это первая стадия всякого статистического исследования, представляющая собой научно организованный, планомерный, систематический сбор и учет массовых данных.
Планомерность статистического наблюдения заключается в том, что проводится оно по разработанному плану, включающему вопросы методологии, организации, техники сбора данных, контроля за качеством собранной информации, ее достоверностью и оформлением результатов.
Систематичность наблюдения обеспечивается тем, что оно проводится непрерывно (регулярно).
Массовый характер статистического наблюдения характеризуется охватом большого числа случаев проявления данного процесса, что позволяет оценить не только отдельные единицы совокупности, но и всю совокупность в целом.
Основными требованиями, предъявляемыми к статистическому наблюдению, являются полнота статистических данных, достоверность данных.
К программно-методологическим вопросам статистического наблюдения относятся вопросы определения цели и задач наблюдения, объекта и единицы наблюдения, составление программы наблюдения, выбор формы статистического формуляра и разработка инструкции.
Объектом наблюдения является совокупность экономических и социально-экономических явлений (процессов), которые подлежат иссле-
дованию, при этом устанавливаются точные границы объекта наблюдения (пределы, в которых регистрируются статистические сведения).
Единица наблюдения – это составная часть или отдельный элемент объекта наблюдения, который служит основой счета и является носителем признаков, подлежащих регистрации при наблюдении. Допустим, объектом наблюдения является население Республики Беларусь, тогда единицей наблюдения является отдельный человек.
Программа наблюдения – это либо перечень вопросов, по которым собираются сведения, либо перечень признаков, подлежащих реги-
страции.
Состав и содержание вопросов программы наблюдения зависят от целей и задач исследования, а также особенностей общественного явления, подвергающегося изучению.
В программу включаются вопросы, безусловно, необходимые для данного исследования. Формироваться они должны четко и однозначно, т. е. должны быть понятны всем одинаково.
Статистический формуляр – это бланк, содержащий перечень вопросов, на которые должны быть получены ответы. Различают следующие виды статистических формуляров:
1. Индивидуальный (карточный) формуляр, в котором отражаются сведения по одной единице наблюдения.
2. Списочный формуляр, содержащий данные по нескольким единицам совокупности.
К статистическим формулярам составляется инструкция, содержащая разъяснения по заполнению формуляров.
К организационным вопросам статистического наблюдения относятся вопросы определения места и органов наблюдения, времени и сроков наблюдения, выбор способа и регистрации данных.
Период, в течение которого проводится наблюдение, называется временем наблюдения (сутки, декада, месяц, квартал, год). Момент времени, на который проводится регистрация сведений, называется критическим моментом наблюдения.
Под сроком наблюдения понимается время начала и окончания сбора сведений.
В статистической практике используются две организационные формы наблюдения: отчетность и специально организованное статистическое наблюдение.
Отчетность – это форма наблюдения, при которой единицы наблюдения представляют сведения о своей деятельности в виде отчетов (формуляров регламентированного образца) в установленные сроки.
Специально организованное статистическое наблюдение проводится в форме переписей, единовременных сплошных и выборочных обследований.
По способу регистрации сведений различают непосредственное наблюдение (фиксируются только факты, непосредственно наблюдаемые), документальную запись (применяется при заполнении форм статистической отчетности, сведения получают из документов первичного учета), опрос (формуляр заполняется со слов опрашиваемого).
Существуют следующие способы собирания сведений:
· экспедиционный (проводит специально подготовленный счетчик);
· корреспондентский (бланки рассылаются обследуемым единицам с просьбой ответить на поставленные вопросы и указаниями по их заполнению);
· саморегистрация (бланк вручается обследуемому лицу с разъяснением его вопросов, заполняется он самостоятельно).
С целью устранения ошибок собранные в результате наблюдения данные проходят контроль: логический (данные формуляров сопоставляют друг с другом, сравнивают с аналогичными данными, полученными из других источников) и счетный (путем последовательного повторения арифметических действий проверяют итоговые и расчетные показатели).
В зависимости от полноты охвата фактов статистическое наблюдение может быть сплошным и несплошным. При сплошном наблюдении производят полный учет всех единиц совокупности. При несплошном наблюдении изучается только часть единиц совокупности. Основными видами несплошного наблюдения являются следующие:
· выборочное наблюдение (характеристика всей совокупности дается по некоторой ее части, отобранной в случайном порядке);
· способ основного массива (наблюдение проводится за частью наиболее крупных единиц, в которых сосредоточена значительная доля всех подлежащих изучению фактов);
· анкетное (кругу лиц вручаются анкеты с просьбой заполнить их и отослать обратно);
· монографическое описание (подробное описание отдельных типичных единиц совокупности).
По учету фактов во времени можно выделить следующие виды статистического наблюдения:
· текущее (регистрируются все случаи, факты по мере их возникновения);
· периодическое (проводится через определенные равные промежутки времени);
· единовременное (проводится по мере возникновения потребности).
Тема 3. СВОДКА И ГРУППИРОВКА СТАТИСТИЧЕСКИХ МАТЕРИАЛОВ. СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Статистическая сводка – это научная обработка первичных данных с целью получения обобщенных характеристик изучаемого явления по ряду существенных для него признаков.
Различают простую и групповую сводки. Простая сводка представляет собой подсчет общих итогов по массе сведений, полученных в результате наблюдения. Групповая сводка проводится по сгруппированным данным.
По способу разработки статистическая сводка может быть централизованной (все данные сосредотачиваются в одном месте и сводятся по единой разработанной методике) и децентрализованной (данные сводятся на местах сбора информации).
Группировкой в статистике называется расчленение единиц статистической совокупности на группы по одному или нескольким существенным признакам. Существенными являются признаки, определяющие основное содержание изучаемого явления, они неразрывно связаны с качеством. Устойчивое разграничение объектов выражается классификацией (каждая атрибутивная запись относится лишь к одной группе, подгруппе, основывается на самых существенных признаках). Группировочный признак – это признак, положенный в основу группировки, он может быть качественным или количественным. Признаки, принимающие разное качественное значение, называются атрибутивными (отражают свойства явлений, не могут быть измерены количественно), а признаки, которые изменяются количественно, называются количественными (могут быть измерены, подсчитаны). Следовательно, и группировки различают по атрибутивным и количественным признакам.
В зависимости от решаемых задач различают следующие виды группировок:
· типологические (выделение социально-экономических типов);
· структурные (расчленение единиц однотипной совокупности на группы по характерным признакам);
· аналитические (выявление связей и зависимостей между явлениями).
Если в основу группировки положен один признак, она является простой. Если же сведения группируются по нескольким признакам, то группировка называется многомерной (сложной).
Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух или более признаках, взятых во взаимосвязи.
При проведении группировки по количественному признаку боль-
шое значение имеет вопрос о количестве групп, на которые будет разделена совокупность. Зависимость между числом групп (n) и численностью единиц совокупности (N) выражается формулой американского ученого Стерджерсса
n = 1 + 3,322 × lg N.
После определения числа групп встает вопрос о размере интервала группировки. Интервал – это разность между максимальным (xmax) и минимальным (xmin) значениями признака в каждой группе. Величина интервала (i) определяется по формуле
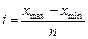 .
.
Интервалы бывают следующих видов:
· равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова;
· неравные, когда эта разность не одинакова;
· специализированные, когда необходимо выделить группы, отличающиеся качественным своеобразием;
· открытые, когда отсутствуют либо верхняя, либо нижняя, либо обе границы;
· закрытые, когда имеются обе границы.
Рассмотрим проведение группировки на примере 1.
Пример 1. Имеются данные о работе потребительских обществ за отчетный период, в млн р. (табл. 1).
Таблица 1
| Потребительское общество | Товарооборот | Расходы на реализацию товаров |
| 1-е | 578,8 | 105,4 |
| 2-е | 1047,2 | 174,9 |
| 3-е | 435,4 | 79,4 |
| 4-е | 930,8 | 156,8 |
| 5-е | 980,0 | 165,2 |
| 6-е | 527,6 | 96,0 |
| 7-е | 1279,2 | 206,8 |
| 8-е | 578,0 | 103,5 |
| 9-е | 944,4 | 158,9 |
| 10-е | 620,8 | 109,4 |
| 11-е | 894,0 | 151,0 |
| 12-е | 532,0 | 96,3 |
| 13-е | 605,6 | 111,4 |
| 14-е | 394,0 | 70,0 |
| 15-е | 516,0 | 94,0 |
| 16-е | 822,4 | 143,9 |
| 17-е | 1254,4 | 202,0 |
| 18-е | 1021,6 | 168,6 |
| 19-е | 580,0 | 106,1 |
| 20-е | 780,8 | 134,3 |
Для выявления зависимости между объемом товарооборота и суммой расходов на реализацию товаров необходимо выполнить следующее:
1. Сгруппировать потребительские общества по размеру розничного товарооборота, образовав четыре группы с равными интервалами.
2. По каждой группе и в целом по всем потребительским обще-
ствам рассчитать нижеуказанные показатели:
· число потребительских обществ;
· объем розничного товарооборота всего и в среднем на одно потребительское общество;
· сумму расходов всего и в среднем на одно потребительское общество.
3. Результаты представить в виде аналитической таблицы, сделать выводы.
Решение
Сначала вычислим величину интервала группировочного признака (товарооборота):
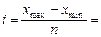
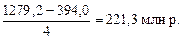
Затем определим границы каждой группы. В первой группе нижняя граница равна хmin. Чтобы определить верхнюю границу, надо к хmin прибавить i (xmin + i). Во второй группе нижняя граница равна верхней границе предыдущей группы. Прибавляя к ней i, вычислим верхнюю границу и т. д. Таким образом, получим следующие границы, в млн р.:
1-й группы – 394,0–615,3;
2-й группы – 615,3–836,6;
3-й группы – 836,6–1057,9;
4-й группы – 1057,9–1279,2.
Данные группировки оформим в виде рабочей таблицы, в млн р. (табл. 2).
Таблица 2
| 1-я группа | 2-я группа | 3-я группа | 4-я группа | ||||
| Товаро- оборот | Расходы | Товаро- оборот | Расходы | Товаро- оборот | Расходы | Товаро- оборот | Расходы |
| 578,8 | 105,4 | 620,8 | 109,4 | 1047,2 | 174,9 | 1279,2 | 206,8 |
| 435,4 | 79,4 | 822,4 | 143,9 | 930,8 | 156,8 | 1254,4 | 202,0 |
| 527,6 | 96,0 | 780,8 | 134,3 | 980,0 | 165,2 | ||
| 578,0 | 103,5 | 944,4 | 158,9 | ||||
| 532,0 | 96,3 | 894,0 | 151,0 | ||||
| 605,6 | 111,4 | 1021,6 | 168,6 | ||||
| 394,0 | 70,0 | ||||||
| 516,0 | 94,0 | ||||||
| 580,0 | 106,1 | ||||||
| Итоговая сумма | |||||||
| 4747,4 | 862,1 | 2224,0 | 387,6 | 5818,0 | 975,4 | 2533,6 | 408,8 |
На основании данных рабочей таблицы и расчета среднего товарооборота и расходов на одно потребительское общество заполним сводную таблицу.
Средний товарооборот на одно потребительское общество по группе 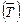 рассчитывается путем деления товарооборота в целом по груп-
рассчитывается путем деления товарооборота в целом по груп-
пе на число потребительских обществ, входящих в группу.
Так, данный показатель по 1-й группе составит
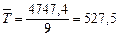 млн р.
млн р.
Аналогично рассчитывается средняя сумма расходов на реализацию товаров на одно потребительское общество 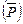 .
.
Например, по 1-й группе указанный показатель составит
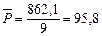 млн р.
млн р.
Результаты представим в виде сводной групповой таблицы (табл. 3).
Таблица 3
| Группы потребительских обществ по размеру розничного товарооборота, млн р. | Число потребительских обществ | Товарооборот, млн р. | Расходы на реализацию товаров, млн р. | ||
| всего | на одно потре- бительское общество | всего | на одно потребительское общество | ||
| 394,0–615,3 | 4747,4 | 527,5 | 862,1 | 95,8 | |
| 615,3–836,6 | 2224,0 | 741,3 | 387,6 | 129,2 | |
| 836,6–1057,9 | 5818,0 | 969,7 | 975,4 | 162,6 | |
| 1057,9–1279,2 | 2533,6 | 1266,8 | 408,8 | 204,4 | |
| Итого | 15323,0 | 766,2 | 2633,9 | 126,7 |
Данные таблицы показывают, что с ростом товарооборота имеет место общая тенденция увеличения суммы расходов.
Группировка, проведенная по первичным данным, называется первичной.
Особым видом в статистике является вторичная группировка. Вторичной группировкой называется образование новых групп на основе ранее проведенной группировки. Применяют следующие способы образования новых групп:
1. Изменение (обычно укрупнение) первоначальных интервалов.
2. Закрепление за каждой группой определенной доли единиц совокупности.
Проведем перегруппировку потребительских обществ по размеру розничного товарооборота в примере 2.
Пример 2. Имеются данные о распределении потребительских обществ двух областей по размеру товарооборота (табл. 4).
Таблица 4
| 1-я область | 2-я область | ||
| группы потребительских обществ по размеру розничного товарооборота, млн р. | число потребительских обществ | группы потребительских обществ по размеру розничного товарооборота, млн р. | число потребительских обществ |
| 300–600 | 300–900 | ||
| 600–900 | 900–1300 | ||
| 900–1200 | 1300–1500 | ||
| 1200–1500 | Свыше 1500 | ||
| Свыше 1500 | |||
| Итого |
Необходимо провести сравнительный анализ распределения потребительских обществ по размеру товарооборота 1-й и 2-й областей и сделать выводы.
Решение
С целью сравнения распределения потребительских обществ по размеру товарооборота двух областей проведем вторичную группировку, приняв за основу сравнения размеры интервалов 2-й области. Результаты перегруппировки потребительских обществ по размеру розничного товарооборота представим в виде табл. 5.
Таблица 5
| Группы потребительских обществ по размеру розничного товарооборота, млн р. | Число потребительских обществ | |
| 1-й области | 2-й области | |
| 300–900 | ||
| 900–1300 | ||
| 1300–1500 | ||
| Свыше 1500 | ||
| Итого |
В первую, вновь образованную, группу потребительских обществ 1-й области с размером товарооборота 300–900 млн р. войдут первые две группы потребительских обществ, их число равно 12 (9 + 3). Вторую группу с размером товарооборота от 900 до 1300 млн р. образуют шесть потребительских обществ с товарооборотом от 900 до 1200 млн р., а также часть группы потребительских обществ с товарооборотом от 1200 до 1500 млн р. ((1300 – 1200) : (1500 – 1200) × 4 = 1 потребительское общество), т. е. всего 7 потребительских обществ (6 + 1).
К группе с товарооборотом от 1300 до 1500 млн р. будут относиться 3 потребительских общества (4 – 1).
Приведя данные к сопоставимому виду, можно осуществить сравнительный анализ распределения потребительских обществ по размеру товарооборота двух областей.
В 1-й области потребительских обществ с размером розничного товарооборота от 300 до 900 млн р. оказалось 50 % 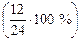 , с то-
, с то-
варооборотом от 900 до 1300 млн р. – 29,2, с товарооборотом от 1300 до 1500 млн р. – 12,5, с товарооборотом свыше 1500 млн р. – 8,3 %. Во 2-й области потребительских обществ с размером товарооборота от 300 до 900 млн р. было 52 % 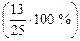 , с товарооборотом от 900 до 1300 млн р. – 20, с товарооборотом от 1300 до 1500 млн р. – 16,
, с товарооборотом от 900 до 1300 млн р. – 20, с товарооборотом от 1300 до 1500 млн р. – 16,
с товарооборотом свыше 1500 млн р. – 12 %.
Статистические таблицы являются средством наглядного выражения результатов исследования. Статистическая таблица имеет подлежащее и сказуемое. В подлежащем отражается объект изучения, в сказуемом – цифровые данные, характеризующие подлежащее.
По построению подлежащего таблицы могут быть простыми, групповыми, комбинационными. В подлежащем простой таблицы нет группировок, в групповой таблице объект разделен на группы по какому-либо признаку, в комбинационной таблице дана группировка единиц совокупности по двум и более признакам, взятым в комбинации.
Простые таблицы бывают следующих видов:
· перечневые (в подлежащем отражается перечень единиц, составляющих объект изучения);
· территориальные (в подлежащем дается перечень территорий, стран, областей, городов и др.);
· хронологические (в подлежащем приводятся периоды времени или даты).
Часто перечень единиц или территорий сочетаются с периодами или моментами времени (перечнево-хронологические и территориально-хронологические таблицы).
Разработка сказуемого таблицы может быть простой (параллельное расположение показателей) и сложной (комбинированное расположение).
Основные правила составления и оформления таблиц следующие:
· Заголовок таблицы должен кратко, но точно раскрывать ее содержание.
· Заглавия строк подлежащего и граф сказуемого должны быть сформулированы кратко, точно и ясно. Графы желательно пронумеровать.
· Если показатели измеряются в одних и тех же единицах измерения, то следует записать их в конце общего заголовка.
· Количественные показатели таблицы должны иметь одинаковую степень точности.
· Не следует загружать таблицу излишними подробностями.
· Признаки, приводимые в таблице, располагают в логическом порядке (обычно от частного к общему).
· Условные обозначения: знак тире «–» означает, что явление отсутствует; знак «´» – что показатель не имеет осмысленного содержания, знак многоточие «¼» – что отсутствуют сведения о размере показателя; знак «0,0» – что величина показателя незначительна и не может быть выражена с точностью, принятой в таблице.
В результате сводки и группировки статистических материалов получают ряды статистических данных, характеризующих изучаемое явление.
Рядом распределения в статистике называется упорядоченное распределение единиц совокупности на группы по какому-либо варьирующему признаку. Распределение по атрибутивным признакам образует атрибутивные ряды распределения, показывающие состав совокупности. Ряды распределения, построенные по количественным признакам, называются вариационными рядами.
В вариационном ряду различают два элемента: варианты и частоты. Вариантами называются отдельные значения группировочного признака (х), а числа, показывающие, как часто встречаются те или иные варианты в ряду распределения, называются частотами ( f ).
По способу построения вариационные ряды делятся на интервальные (значения вариант даны в виде интервалов) и дискретные (варианты в них имеют значения конкретных чисел).
Тема 4. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ
Абсолютные величины характеризуют объем, размер и уровни общественного явления. Выражаются абсолютные величины в натуральных (кг, м, л), условно-натуральных (туб), стоимостных (рубли), трудовых (человеко-часы, человеко-дни), комбинированных (т × км, кВт × ч) единицах измерения.
Относительные величины являются обобщающими показателями, полученными в результате деления двух величин.
Относительные величины подразделяются на следующие виды:
· Относительная величина планового задания, рассчитываемая как отношение планового задания данного (текущего) периода к фактическому уровню предыдущего периода (расчет проводят в процентах).
· Относительная величина выполнения плана – отношение фактического уровня к плановому за один и тот же период (рассчитывается в процентах).
· Относительная величина динамики – отношение фактического уровня данного (текущего) периода к фактическому уровню одного из предыдущих периодов (рассчитывается в коэффициентах или в процентах).
Произведение относительных величин выполнения плана и планового задания равно относительной величине динамики.
· Относительная величина структуры, получаемая как отношение частей совокупности к объему всей совокупности (рассчитывается в процентах).
· Относительная величина сравнения – отношение одноименных показателей, взятых за один и тот же период или момент времени, но характеризующих разные территории или объекты.
· Относительная величина координации – отношение частей совокупности друг к другу.
· Относительная величина интенсивности – соотношение разноименных абсолютных величин, связанных между собой, характеризующее степень распространения явления в определенной среде.
Приведем примеры расчета перечисленных относительных величин (примеры 1–3).
Пример 1. Имеются следующие данные о работе районного потребительского общества (табл. 6).
Необходимо определить следующие относительные величины:
· планового задания;
· выполнения плана;
· динамики.
Кроме того, следует охарактеризовать взаимосвязь показателей.
Таблица 6
| Фактический товарооборот за прошлый год, млн р. | Товарооборот текущего года, млн р. | |
| план | факт | |
Решение
Расчет выполним в следующем порядке:
1. Исчислим относительную величину планового задания (плановый темп роста): 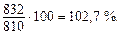 Плановое задание превышает фактический уровень предшествующего периода на 2,7 %.
Плановое задание превышает фактический уровень предшествующего периода на 2,7 %.
2. Определим относительную величину выполнения плана: 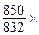
 Плановое задание перевыполнено на 2,2 %.
Плановое задание перевыполнено на 2,2 %.
3. Вычислим относительную величину динамики (фактический темп роста): 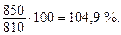 Фактический уровень текущего периода превышает фактический уровень прошлого периода на 4,9 %.
Фактический уровень текущего периода превышает фактический уровень прошлого периода на 4,9 %.
4. Рассчитаем взаимосвязь показателей: 1,027 × 1,022 = 1,049 (104,9 %).
Пример 2. Имеют место следующие данные о работе Гомельского облпотребсоюза (табл. 7).
Таблица 7
| Всего, млн р. | 7163,6 |
| В том числе: | |
| продовольственные товары | 5165,0 |
| непродовольственные товары | 1998,6 |
Следует определить структуру товарооборота.
Решение
Расчет произведем в нижеуказанном порядке:
1. Определим удельный вес продовольственных товаров: 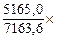
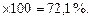
2. Исчислим удельный вес непродовольственных товаров: 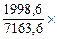
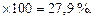
3. Выполним проверку: 72,1 % + 27,9 % = 100,0 %.
Пример 3. Имеется информация о численности населения и площади территорий Гомельской и Могилевской областей (табл. 8).
Таблица 8
| Показатели | Гомельская область | Могилевская область |
| 1. Численность населения, всего, тыс. чел. | 1571,6 | 1236,2 |
| В том числе: | ||
| городского, тыс. чел. | 1090,9 | 876,9 |
| сельского, тыс. чел. | 480,7 | 359,3 |
| 2. Площадь территории, тыс. км2 | 40,4 | 29,1 |
Необходимо определить следующие относительные величины:
· сравнения;
· координации;
· интенсивности.
Решение
Расчет выполним следующим образом:
1. Вычислим относительную величину сравнения. Например, численность населения Гомельской области разделим на численность населения Могилевской области: 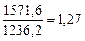 раза. Численность населения Гомельской области в 1,27 раза больше численности населения Могилевской области.
раза. Численность населения Гомельской области в 1,27 раза больше численности населения Могилевской области.
Аналогичный расчет можно провести по городскому и сельскому населению.
2. Определим относительную величину координации. Например, численность городского населения Гомельской области разделим на численность сельского населения Гомельской области: 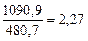 раза. Численность городского населения в 2,27 раза больше численности сельского населения.
раза. Численность городского населения в 2,27 раза больше численности сельского населения.
Аналогично можно провести расчет по Могилевской области.
3. Исчислим относительную величину интенсивности. Численность населения Гомельской области разделим на площадь территории области: 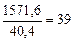 чел. на 1 км2. Таким образом, на 1 км2 поживает 39 чел.
чел. на 1 км2. Таким образом, на 1 км2 поживает 39 чел.
Аналогично можно провести расчет по Могилевской области.
Тема 5. СРЕДНИЕ ВЕЛИЧИНЫ
5.1. Понятие о средней величине
Средняя величина является обобщающей количественной характеристикой изучаемого признака в исследуемой совокупности. В статистике используются различного рода средние величины.
Средняя арифметическая – частное от деления суммы вариант на их число. Она бывает следующих видов: простая или взвешенная.
Средняя арифметическая простая, рассматривается в случае, когда известны все значения признаков х1, х2, ¼, хп и рассчитывается по формуле
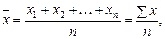
где n – число вариант;
х – значение признака.
Средняя арифметическая взвешенная, исчисляется, если известны отдельные значения признаков и их частоты, по следующей формуле:
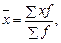
где х – значение признака;
f – частота, которая может быть абсолютной (в разах) и относительной (доля, удельный вес частот во всей совокупности) величиной.
Средняя арифметическаяимеет следующие свойства:
· произведение средней арифметической на сумму частот равно сумме произведений вариант на соответствующие им частоты;
· если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число;
· если все варианты увеличить или уменьшить в одно и то же число раз, то средняя арифметическая увеличится или уменьшится во столько же раз;
· если все частоты одинаково увеличить или уменьшить в одно и то же число раз, то средняя арифметическая не изменится;
· сумма отклонений вариант от их средней арифметической величины равна нулю.
Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Данный показатель применяется тогда, когда неизвестна численность совокупности и приходится взвешивать варианты по объемам признака. Средняя гармоническая также может быть простой и взвешенной.
Средняя гармоническая простая исчисляется по формуле
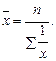
Средняя гармоническая взвешенная рассчитывается по следующей формуле:
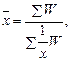
где W = xf – вес средней гармонической.
Средняя квадратическая (и т. д. для любой степени) рассчитывается по следующим формулам:
· простая: 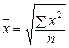
· взвешенная: 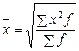
Средняя геометрическая определяется по следующим формулам:
· простая: 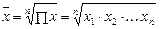 ,
,
где Π – знак перемножения.
· взвешенная: 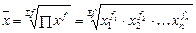 .
.
В экономической практике чаще всего приходится употреблять среднюю арифметическую (простую и взвешенную) и среднюю гармоническую взвешенную.
Рассмотрим их применение на следующих типовых примерах.
Пример 1. Имеются следующие данные о размере торговой площади магазинов, входящих в районное потребительское общество (табл. 9).
Таблица 9
| Магазин | 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | 7-й | 8-й | 9-й | 10-й |
| Площадь магазина, м2 |
Необходимо определить среднюю площадь магазина.
Решение
Так как известна площадь каждого магазина, то для вычисления средней площади магазина 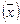 следует применить среднюю арифметическую простую:
следует применить среднюю арифметическую простую:
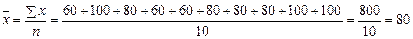 м2.
м2.
Средняя площадь магазина составляет 80 м2.
Пример 2. Приведенные данные в предыдущем примере могут быть представлены в сгруппированном виде (табл. 10).
Таблица 10
| Площадь магазинов, м2 (признак – х) | |||
| Число магазинов (частота – f ) |
Необходимо определить среднюю площадь магазина.
Решение
Если известны отдельные значения признака и соответствующие ему частоты, то применяется средняя арифметическая взвешенная:
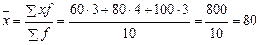 м2.
м2.
Средняя площадь магазина составляет 80 м2.
Пример 3. Имеются следующие данные о распределении магазинов по торговой площади (табл. 11).
Таблица 11
| Группировка магазинов по торговой площади, м2 (признак – х) | Удельный вес магазинов в общей численности, % (частость – f ) |
| 40–60 | |
| 60–80 | |
| 80–100 | |
| Итого |
Следует определить среднюю площадь магазина.
Решение
Известны отдельные значения признака и их частоты, следовательно, следует применять среднюю арифметическую взвешенную:
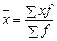 .
.
Так как варианты представлены в виде интервального ряда распределения, то, чтобы воспользоваться указанной формулой, необходимо выразить их одним числом, т. е. следует перейти к дискретному ряду распределения (в этом случае находят середину каждого интервала).
Для первого интервала 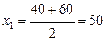 м2 и т. д. по остальным интервалам. Расчеты следует производить в табл. 12.
м2 и т. д. по остальным интервалам. Расчеты следует производить в табл. 12.
Таблица 12
| Группировка магазинов по торговой площади, м2 (х) | Удельный вес магазинов в общей численности, % ( f ) | Середина интервала (х) | xf |
| 40–60 | |||
| 60–80 | |||
| 80–100 | |||
| Итого | – |
Таким образом, 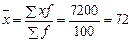 м2.
м2.
Средняя площадь магазина равна 72 м2.
Пример 4. Имеются следующие данные о распределении магазинов по площади (табл. 13).
Таблица 13
| Площадь магазинов, м2 (признак – х) | Общая площадь магазинов, входящих в данную группу, м2 (w = xf ) |
| Итого |
Необходимо определить среднюю площадь магазина.
Решение
Так как весами является площадь W = xf, то следует применять среднюю гармоническую взвешенную:
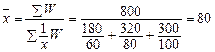 м2.
м2.
Таким образом, средняя площадь магазина равна 80 м2.
5.2. Вычисление средней из вариационного ряда
«способом моментов»
«Способ моментов» применяется в рядах с равными интервалами на основе свойств средней арифметической. Средняя арифметическая исчисляется по формуле
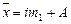 ,
,
где i – размер интервала;
m1 – момент первого порядка (средняя арифметическая из новых упрощенных вариант 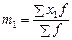 ;
; 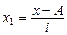 – новые упрощенные варианты; f – частота);
– новые упрощенные варианты; f – частота);
А – постоянное число (лучше всего взять его равным варианте, у которой наибольшая частота).
Определим среднее значение признака «способом моментов» на следующем примере.
Пример 5. Имеются следующие данные о распределении магазинов облпотребсоюза по торговой площади (табл. 14).
Таблица 14
| Группировка магазинов по торговой площади, м2 (х) | Удельный вес магазинов, % ( f ) |
| До 40 | |
| 40–60 | |
| 60–80 | |
| 80–100 | |
| Свыше 100 | |
| Итого |
Следует определить среднюю площадь магазинов, применив «способ моментов».
Решение
Данные распределения магазинов по торговой площади представлены в виде интервального ряда распределения с равными интервалами (i = 20 м2), следовательно, расчет средней площади магазина можно провести по формуле  , применив «способ моментов».
, применив «способ моментов».
Первый и последний интервалы даны открытыми, т. е. не имеют границ нижней и верхней соответственно. Для определения среднего значения в них границы интервалов следует закрыть. Для первой группы с размером площади до 40 м2 условно считаем, что интервал также равен 20 м2, затем вычитаем 20 м2 из 40 м2 и находим условную нижнюю границу первого интервала (20 – 40). Условную верхнюю границу последнего интервала определяем аналогично (100 – 120).
Расчеты следует проводить в табл. 15.
Таблица 15
| Группировка мага- зинов по торговой площади, м2 (х) | Удельный вес магазинов, % (f) | Середина интервала (х) | х – А | 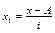
| xf |
| 20–40 | –40 | –2 | –10 | ||
| 40–80 | –20 | –1 | –30 | ||
| 60–80 | |||||
| 80–100 | |||||
| 100–120 | |||||
| Итого | – | – | – | –10 |
Наибольшая частота f равна 40, следовательно, в качестве постоянной величины А принимаем 70.
Определяем момент первого порядка: 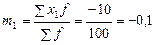 .
.
Среднее значение признака равно: 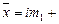
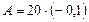 + 70 =
+ 70 =
= 68 м2.
Следовательно, средняя площадь магазина составляет 68 м2.
5.3. Структурные средние
В качестве структурных средних чаще всего используют показатели моды и медианы. Мода (Мо) – наиболее часто повторяющееся значение признака. Медиана (Ме) – величина признака, которая делит упорядоченный ряд на две равные по численности части.
Если расчет моды и медианы проводится в дискретном ряду, то он опирается на их понятия. В интервальном ряду распределения для расчета моды и медианы применяют следующие формулы.
Мода рассчитывается по формуле
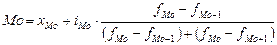 ,
,
где хМо – нижнее значение модального интервала;
iМо – размер модального интервала;
fМо – частота модального интервала;
fМо–1 – частота, предшествующая модальной частоте;
fМо+1 – частота, последующая за модальной частотой.
Модальному интервалу соответствует наибольшая (модальная) частота. Медиана рассчитывается по формуле
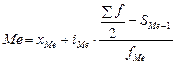 ,
,
где хМе – нижнее значение медианного интервала;
iМе – размер медианного интервала;
Sf – сумма частот;
SМе–1 – сумма частот, предшествующих медианной частоте;
fМе – медианная частота.
Медианному интервалу соответствует медианная частота. Таким интервалом будет интервал, сумма накопленных частот которого равна или превышает половину суммы всех частот.
Рассмотрим определение моды и медианы на следующих примерах.
Пример 6. В результате статистического обследования области получены следующие данные по распределению семей по числу детей (табл. 16).
Таблица 16
| Число детей (х) | Количество семей, в % к итогу ( f ) |
| 6 и более | |
| Итого |
Следует определить моду и медиану.
Решение
В дискретных рядах модой является варианта с наибольшей частотой. Наибольшая частота – 34, следовательно мода равна 2.
Для вычисления медианы определим сумму частот ряда (Sf = 100), затем рассчитаем полусумму 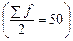 .
.
Так как сумма накопленных частот 5 + 32 + 34 = 71 превышает полусумму (71 > 50), то варианта, имеющая значение 2 и соответствующая этой накопленной сумме частот, и есть медиана.
Пример 7. В результате статистического обследования получены следующие данные распределения продавцов магазинов облпотребсоюза по возрасту (табл. 17).
Таблица 17
| Группировка продавцов по возрасту, лет (х) | Удельный вес продавцов, % ( f ) |
| До 20 | |
| 20–30 | |
| 30–40 | |
| Окончание табл. 17 | |
| Группировка продавцов по возрасту, лет (х) | Удельный вес продавцов, % ( f ) |
| 40–50 | |
| Свыше 50 | |
| Итого |
Необходимо определить моду и медиану.
Решение
В интервальных рядах мода и медиана определяются по вышеприведенным формулам.
Сначала определим модальный интервал, он соответствует наибольшей частоте. Так как наибольшая частота равна 35 и является модальной, то интервал 30–40 является модальным интервалом. Затем подставим данные в следующую формулу:
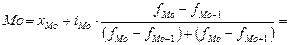
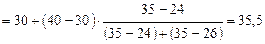 лет.
лет.
Определим медианный интервал. Полусумма частот равна 50 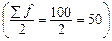 . Накапливая частоты, определим интересующий интервал. Так как сумма накопленных частот 6 + 24 + 35 = 65 превышает полусумму (65 > 50), значит 35 является медианной частотой, а интервал 30–40 является медианным интервалом.
. Накапливая частоты, определим интересующий интервал. Так как сумма накопленных частот 6 + 24 + 35 = 65 превышает полусумму (65 > 50), значит 35 является медианной частотой, а интервал 30–40 является медианным интервалом.
Затем подставим данные в формулу
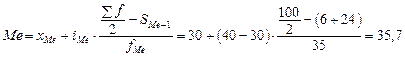 .
.
Таким образом, мода равна 35,5 лет (больше всего продавцов
в возрасте 35,5 лет), медиана – 35,7 лет (50 % продавцов достигли возраста 35,7 лет).
Тема 6. ПОКАЗАТЕЛИ ВАРИАЦИИ
6.1. Понятие вариации признаков. Показатели вариации
Средние величины дают обобщенную характеристику варьирующего признака, но в них не отражается степень колеблемости отдельных значений признака вокруг среднего уровня. Для измерения колеблемости изучаемого признака в статистике применяются различные показатели.
1. Размах вариации (R) определяется по формуле
R = хмах – хmin,
где хmin – минимальное значение признака;
хmах – максимальное значение признака.
Этот показатель дает общее, внешнее представление о колеблемости признака, но не характеризует степень его колебаний.
2. Среднее линейное отклонение 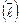 исчисляется по следующим формулам:
исчисляется по следующим формулам:
· по несгруппированным данным: 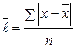 ;
;
· по сгруппированным данным: 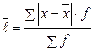 .
.
Этот показатель представляет собой среднюю величину из отклонений индивидуальных значений признака от средней арифметической. Как меру вариации признака этот показатель в статистике применяют редко.
3. Дисперсия признака (σ2) рассчитывается следующим образом:
· по несгруппированным данным: 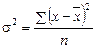 ,
,
· по сгруппированным данным: 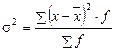 .
.
Дисперсия является средней арифметической квадратов отклонений каждого значения признака от общей средней, это относительная мера вариации.
4. Среднее квадратическое отклонение 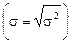 – это абсолютная мера вариации, выражается в единицах измерения изучаемого признака и определяется по следующим формулам:
– это абсолютная мера вариации, выражается в единицах измерения изучаемого признака и определяется по следующим формулам:
· по несгруппированным данным: 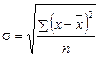 ;
;
· по сгруппированным данным: 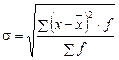 .
.
5. Коэффициент вариации (V) применяется для сравнения степени вариации различных признаков, выражается в процентах и определяется следующим образом:
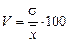 .
.
Рассмотрим определение дисперсии признака, среднего квадратического отклонения и коэффициента вариации на следующем примере.
Пример 1. Имеются следующие статистические данные о возраст-
ном составе работающих по возрасту (табл. 18).
Таблица 18
| Группировка работающих по возрасту, лет (х) | Удельный вес работающих, % ( f ) |
| До 20 | |
| 20–30 | |
| 30–40 | |
| 40–50 | |
| Свыше 50 | |
| Итого |
Решение
Так как данные представлены в сгруппированном виде, то для расчета следует применить следующие формулы:
· дисперсии: 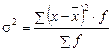 ,
,
где 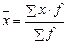 ;
;
· среднего квадратического отклонения: 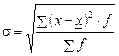 ;
;
· коэффициента вариации: 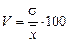 .
.
Сначала определим условные нижнюю и верхнюю границы первого и последнего интервала, затем от интервального ряда перейдем к дискретному ряду.
Расчеты следует проводить в табл. 19.
Таблица 19
| Группировка ра- ботающих по возрасту, лет (х) | Удельный вес работающих, % ( f ) | Середина интервала (х) | x × f | 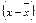
| 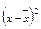
| 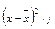
|
| До 20 | –23,6 | 556,96 | 2227,84 | |||
| 20–30 | –13,6 | 184,96 | 3699,2 | |||
| 30–40 | –3,6 | 12,96 | 388,8 | |||
| 40–50 | 6,4 | 40,96 | 1146,88 | |||
| Свыше 50 | 16,4 | 268,96 | 4841,28 | |||
| Итого | – | – | – |
Определим следующие показатели:
· среднее значение признака по формуле 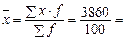
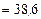 лет;
лет;
· дисперсию по следующей формуле: 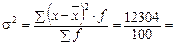
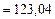 ;
;
· среднее квадратическое отклонение по формуле 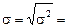
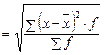
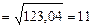 лет;
лет;
· коэффициент вариации следующим образом: 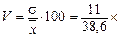
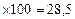 %. Если V > 33 %, то это говорит о большой колеблемости признака в изучаемой совокупности.
%. Если V > 33 %, то это говорит о большой колеблемости признака в изучаемой совокупности.
| <== предыдущая страница | | | следующая страница ==> |
| E Сигмовидной ободочной | | | Развитие представлений о предмете психологии |
Дата добавления: 2014-10-14; просмотров: 629; Нарушение авторских прав

Мы поможем в написании ваших работ!