
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Часть 1. Для самостоятельной работы студентов по курсу
СБОРНИК ЗАДАНИЙ
Для самостоятельной работы студентов по курсу
«Дифференциальные уравнения»
(факультет ИТС МИЭТ)
Часть 1
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
1-го ПОРЯДКА
Учебное пособие
Утверждено методическим советом кафедры ВМ-2
Зав. кафедры С. Г. Кальней
Москва
Прочти, реши и опять прочти!..
АННОТАЦИЯ
Сборник содержит систематизированный набор задач по основным разделам предмета «Дифференциальные уравнения» в части дифференциальных уравнений 1-го порядка. Основная цель Сборника – предоставить студентам стандартный набор задач для самостоятельной доработки материала Предмета.
По каждой теме, представленной в Сборнике, приведены примеры применения общих алгоритмов, полученных в теории дифференциальных уравнений. Учитывается, что общие алгоритмы достаточно отработаны на семинарских занятиях и при выполнении текущих домашних заданий и не нуждаются в их обосновании.
При оформлении каждого выполненного задания студенты должны руководствоваться иллюстрирующими примерами Сборника: применение общих алгоритмов должно сопровождаться краткими комментариями и пояснениями.
ОГЛАВЛЕНИЕ
Стр.
Аннотация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Часть 1. Дифференциальные уравнения (ДУ) 1-го порядка.
1.1. Для заданного семейства кривых 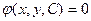 составить дифференциальное уравнение . . . 5
составить дифференциальное уравнение . . . 5
1.2. Решить дифференциальное уравнение с разделяющимися переменными . . . . . . . . . . . . . . . . 6
1.3. Решить однородное дифференциальное уравнение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.4. Решить линейное дифференциальное уравнение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.5. Решить дифференциальное уравнение Бернулли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.6. Решить уравнение в полных дифференциалах . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.7. Используя ДУ 1-го порядка, найти уравнение кривой с заданными свойствами . . . . . . . . . . . 18
1.8. Используя ДУ 1-го порядка, решить задачи из физики и химии . . . . . . . . . . . . . . . . . . . . . . . . . 26
1.9. Дополнительные задачи к Части 1: решить уравнения Лагранжа и Клеро . . . . . . . . . . . . . . . . . 38
•◄●►•
Часть 1. Дифференциальные уравнения (ДУ) 1-го порядка.
1.1. Для заданного семейства кривых 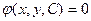 составить дифференциальное уравнение.
составить дифференциальное уравнение.
Общие сведения. Известно, что общее решение дифференциального уравнения 1-го порядка может быть представлено в виде выражения: 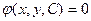 , где
, где 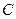 − произвольная постоянная величина. Учитывая Теорему о существовании и единственности решения дифференциального уравнения, можем утверждать, что при выполнении требований Теоремы в области
− произвольная постоянная величина. Учитывая Теорему о существовании и единственности решения дифференциального уравнения, можем утверждать, что при выполнении требований Теоремы в области 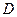 каждому (допустимому) значению
каждому (допустимому) значению 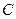 соответствует кривая линия. Учитывая традиции математики: каждой прямой операции определять обратную, поставим вопрос – А нельзя ли, имея функцию
соответствует кривая линия. Учитывая традиции математики: каждой прямой операции определять обратную, поставим вопрос – А нельзя ли, имея функцию 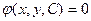 , где
, где 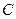 − параметр, найти такое дифференциальное уравнение (обратная операция), для которого функция
− параметр, найти такое дифференциальное уравнение (обратная операция), для которого функция 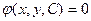 была бы решением?..
была бы решением?..
Задача: Пусть задано семейство кривых: 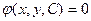 , где
, где 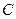 − параметр. Будем считать, что функция
− параметр. Будем считать, что функция 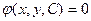 определяет неявную функцию
определяет неявную функцию 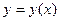 (хотя при помощи этой же функции может быть определена неявная функция
(хотя при помощи этой же функции может быть определена неявная функция 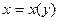 ). Необходимо составить дифференциальное уравнение, решением которого является это семейство.
). Необходимо составить дифференциальное уравнение, решением которого является это семейство.
Общая схема решения задачи:
1). Используя функцию 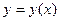 , запишем тождество:
, запишем тождество: 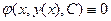 . Левая часть этого тождества представляет собой сложную функция переменной
. Левая часть этого тождества представляет собой сложную функция переменной 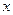 , которая тождественно равна нулю. Тогда и производная её по переменной
, которая тождественно равна нулю. Тогда и производная её по переменной 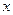 также есть нуль. Дифференцируя это тождество по переменной
также есть нуль. Дифференцируя это тождество по переменной 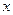 , получим:
, получим: 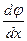 =
=  =
= 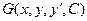
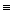 0.
0.
2). Запишем систему:  Исключив параметр
Исключив параметр 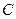 из этой системы, получим выражение, содержащее только переменные
из этой системы, получим выражение, содержащее только переменные  − дифференциальное уравнение, решением которого является семейство кривых:
− дифференциальное уравнение, решением которого является семейство кривых: 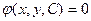 .
.
3). Оформляем результат решения задачи – записываем Ответ.
Замечание: В виде подсказки: каждый студент должен знать, что все Задания подобраны так, чтобы указанная система имела вполне простое решение!..
Пример (и образец оформления):
Пример 1.1. Имеем семейство кривых: 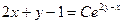 . Необходимо построить дифференциальное уравнение, для которого данное семейство кривых является решением.
. Необходимо построить дифференциальное уравнение, для которого данное семейство кривых является решением.
Решение:
1). Считая, что выражение 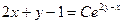 определяет неявную функцию
определяет неявную функцию 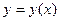 , продифференцируем это выражение по независимой переменной
, продифференцируем это выражение по независимой переменной 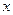 . Имеем:
. Имеем: 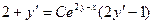 .
.
2). Запишем систему: 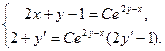 Для исключения из системы параметра
Для исключения из системы параметра 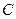 умножим первое равенство на скобку
умножим первое равенство на скобку  : правые части первого и второго равенств оказались равными. Но тогда равны и левые части первого и второго равенств:
: правые части первого и второго равенств оказались равными. Но тогда равны и левые части первого и второго равенств: 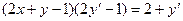 − получено дифференциальное уравнение 1-го порядка, решением которого является заданное семейство кривых.
− получено дифференциальное уравнение 1-го порядка, решением которого является заданное семейство кривых.
Ответ: семейство кривых: 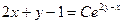 является решением дифференциального уравнения:
является решением дифференциального уравнения: 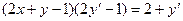 , или
, или 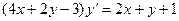 .
.
Задание 1.1. Составить ДУ для семейства кривых:
| Вар. | Семейство: | Вар. | Семейство: |
| 1.1.1. | 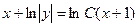 . .
| 1.1.16. | 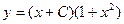 . .
|
| 1.1.2. |  . .
| 1.1.17. |  . .
|
| 1.1.3. | 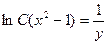 . .
| 1.1.18. | 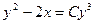 . .
|
| 1.1.4. | 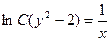 . .
| 1.1.19. | 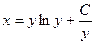 . .
|
| 1.1.5. | 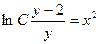 . .
| 1.1.20. | 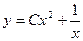 . .
|
| 1.1.6. | 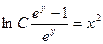 . .
| 1.1.21. | 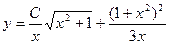 . .
|
| 1.1.7. | 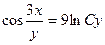 . .
| 1.1.22. | 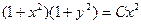 . .
|
| 1.1.8. | 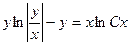 . .
| 1.1.23. |  . .
|
| 1.1.9. | 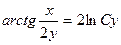 . .
| 1.1.24. | 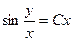 . .
|
| 1.1.10. |  . .
| 1.1.25. | 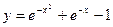 . .
|
| 1.1.11. | 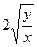 = = 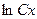 . .
| 1.1.26. |  . .
|
| 1.1.12. | 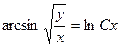 . .
| 1.1.27. | 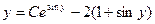 . .
|
| 1.1.13. | 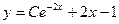 . .
| 1.1.28. |  . .
|
| 1.1.14. | 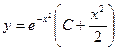 . .
| 1.1.29. | 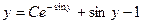 . .
|
| 1.1.15. | 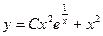 . .
| 1.1.30. |  . .
|
1.2. Решить дифференциальное уравнение с разделяющимися переменными.
Общие сведения. Для выполнения задания требуется знать, что решить дифференциальное уравнение – это значит найти все его решения. Известно, что дифференциальное уравнение 1-го порядка может быть задано и в форме  с использованием производной, и в форме
с использованием производной, и в форме 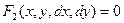 с использованием дифференциалов. Так как решение (интегрирование) уравнения предполагает в любом случае использование записи
с использованием дифференциалов. Так как решение (интегрирование) уравнения предполагает в любом случае использование записи 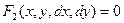 , будем считать, что преобразование
, будем считать, что преобразование 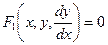 →
→ 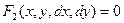 всегда осуществимо (с учётом требований тождественности).
всегда осуществимо (с учётом требований тождественности).
Замечание: Задания подобраны так, что выражение 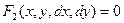 достаточно просто преобразуется к специальной форме записи:
достаточно просто преобразуется к специальной форме записи: 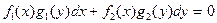 . (1.1)
. (1.1)
Задача: Задано дифференциальное уравнение: 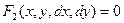 . Показать, что уравнение является уравнением с разделяющимися переменными. Найти общее решение заданного уравнения.
. Показать, что уравнение является уравнением с разделяющимися переменными. Найти общее решение заданного уравнения.
Общая схема решения задачи:
1). В заданном уравнении 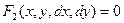 указываем признаки уравнения с разделяющимися переменными: возможность получить запись уравнения (1.1). Разделяем в заданном уравнении переменные
указываем признаки уравнения с разделяющимися переменными: возможность получить запись уравнения (1.1). Разделяем в заданном уравнении переменные 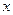 и
и 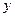 . В результате получим общую запись:
. В результате получим общую запись:
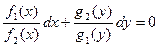 . (1.2)
. (1.2)
2). Для перехода к записи (1.2) выполнялось деление на функции: 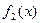 и
и 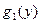 . Если возможны равенства:
. Если возможны равенства:  и
и 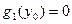 , необходимо функции:
, необходимо функции:  и
и 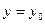 учесть как решения исходного уравнения.
учесть как решения исходного уравнения.
3). Интегрируя уравнение (1.2), получим общее решение исходного уравнения (1.1) в виде выражения: 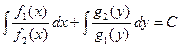 .
.
Замечание: Все Задания подобраны так, чтобы вычисление неопределённых интегралов не вызывало серьёзных затруднений!..
4). Оформляем результат решения задачи – записываем Ответ.
Пример (и образец оформления):
Пример 1.2. Решить дифференциальное уравнение 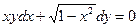 .
.
Решение:
1). Заданное уравнение есть уравнение с разделяющимися переменными: в соответствии с записью (1.1) имеем 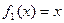 ;
; 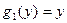 и
и  ;
; 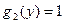 . Так как
. Так как 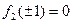 и
и 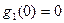 , то функции:
, то функции: 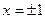 и
и  необходимо учесть как решения исходного уравнения.
необходимо учесть как решения исходного уравнения.
2). Теперь считаем, что 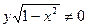 . Разделив заданное уравнение на
. Разделив заданное уравнение на 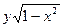 , получим уравнение:
, получим уравнение:  – переменные разделились.
– переменные разделились.
3). В результате интегрирования получаем общее решение уравнения в виде 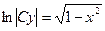 или
или 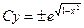 . Учитывая, что
. Учитывая, что 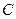 − произвольная постоянная величина, запишем общее решение в виде:
− произвольная постоянная величина, запишем общее решение в виде: 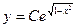 . При
. При 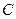 =0 из общего решения получаем также решение
=0 из общего решения получаем также решение  .
.
Ответ: 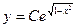 - общее решение (содержит также решение y = 0);
- общее решение (содержит также решение y = 0); 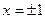 .
.
Задание 1.2. Решить уравнение с разделяющимися переменными:
| Вар. | Уравнение: | Вар. | Уравнение: |
| 1.2.1. | 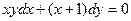
| 1.2.16. | 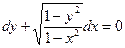
|
| 1.2.2. | 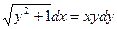
| 1.2.17. | 
|
| 1.2.3. | 
| 1.2.18. | 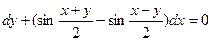
|
| 1.2.4. | 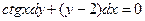
| 1.2.19. | 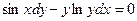
|
| 1.2.5. | 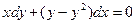
| 1.2.20. | 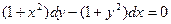
|
| 1.2.6. | 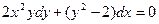
| 1.2.21. | 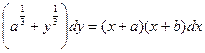
|
| 1.2.7. | 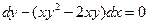
| 1.2.22. | 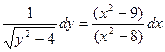
|
| 1.2.8. | 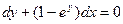
| 1.2.23. | 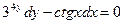
|
| 1.2.9. | 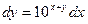
| 1.2.24. | 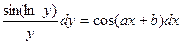
|
| 1.2.10. | 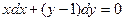
| 1.2.25. | 
|
| 1.2.11. | 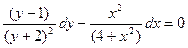
| 1.2.26. | 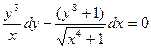
|
| 1.2.12. | 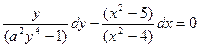
| 1.2.27. | 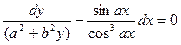
|
| 1.2.13. | 
| 1.2.28. | 
|
| 1.2.14. | 
| 1.2.29. | 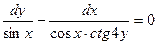
|
| 1.2.15. | 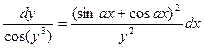
| 1.2.30. | 
|
1.3. Решить однородное дифференциальное уравнение.
Общие сведения. Для выполнения задания требуется знать, что решить дифференциальное уравнение – это значит найти все его решения. Также важно знать, что однородное дифференциальное уравнение 1-го порядка названо однородным из-за применения понятия однородная функция. Однородные дифференциальные уравнения интересны также тем, что легко распознаются среди других дифференциальных уравнений и имеют хорошо формализованный алгоритм решения. На первом этапе изучения дифференциальных уравнений это также важно! Различают записи однородного уравнения: 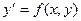 , где
, где  – однородная функция нулевого порядка, и
– однородная функция нулевого порядка, и 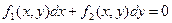 , где функции
, где функции 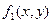 и
и  однородные одного порядка. Каждой из этих форм записи отвечает свой стандартный алгоритм решения!..
однородные одного порядка. Каждой из этих форм записи отвечает свой стандартный алгоритм решения!..
Замечание: Так как между записями дифференциального уравнения в форме, использующей производную:  и в форме дифференциалов:
и в форме дифференциалов: 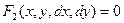 легко установить взаимно однозначное соответствие, любое из Заданий может быть решено любым из представленных Способов – по выбору!..
легко установить взаимно однозначное соответствие, любое из Заданий может быть решено любым из представленных Способов – по выбору!..
Задача: Имеем дифференциальное уравнение: 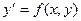 . Показать, что уравнение является однородным и может быть приведено к форме записи
. Показать, что уравнение является однородным и может быть приведено к форме записи 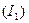 :
: 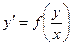 . Найти общее решение заданного уравнения.
. Найти общее решение заданного уравнения.
Общая схема решения задачи 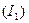 :
:
1). В заданном уравнении выделяем признак однородного уравнения и записываем его в форме 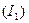 : при этом соблюдаем требования тождественности преобразований – не потерять очевидные решения. Для решения уравнения применяем подстановку:
: при этом соблюдаем требования тождественности преобразований – не потерять очевидные решения. Для решения уравнения применяем подстановку: 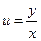 , то есть
, то есть 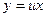 .
.
2). Так мы хотим, чтобы функция 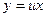 была решением уравнения (1), необходимо подставить её в исходное уравнение (по определению!)!.. Так как
была решением уравнения (1), необходимо подставить её в исходное уравнение (по определению!)!.. Так как 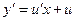 , после подстановки
, после подстановки 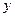 и
и 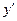 в
в 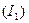 получаем:
получаем: 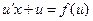 , или (так как
, или (так как 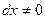 ):
):
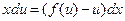 . (1.3)
. (1.3)
3). Уравнение (1.3) есть уравнение с разделяющимися переменными! Исследуем равенство: 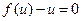 . Если имеется такое число
. Если имеется такое число 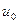 , что
, что  , то
, то  , или
, или 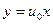 есть решение уравнения
есть решение уравнения 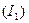 .
.
4). Теперь примем: 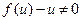 . Уравнение (1.3) запишем в виде:
. Уравнение (1.3) запишем в виде: 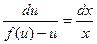 . Его интегрирование даёт общий интеграл (решение):
. Его интегрирование даёт общий интеграл (решение): 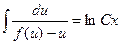 . Будем считать, что интеграл удалось вычислить:
. Будем считать, что интеграл удалось вычислить:  . Если в последнем заменить
. Если в последнем заменить 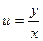 , получим общий интеграл уравнения
, получим общий интеграл уравнения 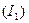 :
: 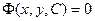 .
.
5). Оформляем результат решения задачи – записываем Ответ.
Пример (и образец оформления):
Пример 1.3. Решить дифференциальное уравнение 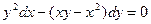 .
.
Решение:
1). Прежде всего, отметим, что исходное уравнение имеет очевидные решения: 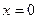 и
и 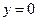 .
.
2). В заданном уравнении указываем признаки однородного уравнения и записываем его в виде (скажем, автору больше нравится этот способ решения): 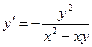 =
= 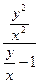 .
.
3). Примем 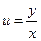 и запишем выражение:
и запишем выражение: 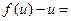
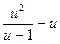 =
= 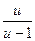 . Исследуем равенство:
. Исследуем равенство: 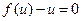 , в нашем случае
, в нашем случае 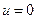 – повторяет уже имеющееся
– повторяет уже имеющееся 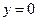 .
.
4). Теперь примем 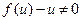 и вычислим интеграл
и вычислим интеграл 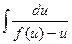 =
= 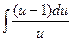 =
= 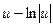 .
.
5). Для функции 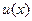 получено общее решение:
получено общее решение: 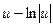 =
= 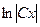 , или
, или  . Учитывая, что
. Учитывая, что 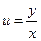 , перепишем общее решение использованием
, перепишем общее решение использованием 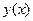 :
:  .
.
Ответ:  – общее решение ДУ, также
– общее решение ДУ, также 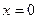 и
и 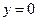 , причём решение
, причём решение 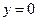 формально можно выделить из общего при значении
формально можно выделить из общего при значении 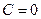 .
.
Задача: Имеем дифференциальное уравнение 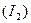 :
: 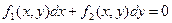 . Показать, что уравнение является однородным и может быть решено заменой
. Показать, что уравнение является однородным и может быть решено заменой 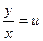 . Найти общее решение заданного уравнения.
. Найти общее решение заданного уравнения.
Замечание: Учитывая опыт решения Задачи 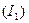 , нетрудно догадаться, что и при решении Задачи
, нетрудно догадаться, что и при решении Задачи 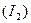 может быть построен стандартный алгоритм решения однородного уравнения, который удобно применять в случаях
может быть построен стандартный алгоритм решения однородного уравнения, который удобно применять в случаях 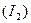 .
.
Общая схема решения задачи 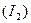 :
:
1). Выделяем признаки однородного уравнения: функции 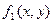 и
и 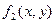 однородные функции одного порядка. Переписываем заданное дифференциальное уравнение
однородные функции одного порядка. Переписываем заданное дифференциальное уравнение 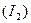 в виде:
в виде:
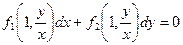 . (1.3’)
. (1.3’)
2). Для перехода к записи (1.3’) выполнялось деление на число 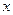 . Нужно проверить, не является ли решением функция
. Нужно проверить, не является ли решением функция 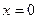 . Если возможны равенства:
. Если возможны равенства: 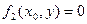 и
и 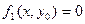 , необходимо также функции:
, необходимо также функции:  и
и 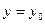 учесть как решения исходного уравнения.
учесть как решения исходного уравнения.
3). Применим замену: 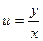 , то есть
, то есть 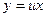 . Вычислим:
. Вычислим: 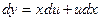 . Подставим
. Подставим  и
и 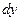 в уравнение (1.3’):
в уравнение (1.3’):  . (1.4)
. (1.4)
4). Так как уравнение (1.4) есть уравнение с разделяющимися переменными  и
и 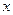 , то остаётся применить общий алгоритм решения дифференциальных уравнений с разделяющимися переменными как в разделе (1.2). Решив уравнение (1.4), используя замену
, то остаётся применить общий алгоритм решения дифференциальных уравнений с разделяющимися переменными как в разделе (1.2). Решив уравнение (1.4), используя замену 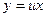 , записываем решение исходного уравнения
, записываем решение исходного уравнения 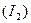 .
.
5). Оформляем результат решения задачи – записываем Ответ.
Пример (и образец оформления):
Пример 1.3. Решить дифференциальное уравнение 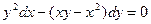 .
.
Решение:
1). Легко заметить, что в нашем случае 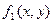 =
= 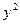 и
и 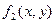 =
= 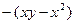 − однородные функции 2-го порядка. Это значит, заданное уравнение – однородное уравнение. Решаем уравнение применением замены:
− однородные функции 2-го порядка. Это значит, заданное уравнение – однородное уравнение. Решаем уравнение применением замены: 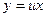 , то есть
, то есть 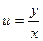 .
.
2). Используя 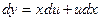 , перепишем уравнение:
, перепишем уравнение: 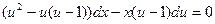 – уравнение с разделяющимися переменными
– уравнение с разделяющимися переменными  и
и 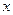 . Для полученного уравнения выделим очевидные решения:
. Для полученного уравнения выделим очевидные решения:  =0, то есть
=0, то есть  и
и 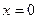 .
.
3). После этого запишем уравнение в виде: 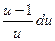 =
=  , которое легко интегрируется:
, которое легко интегрируется: 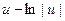 =
= 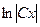 , или
, или 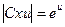 , или
, или 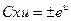 . Учитывая, что
. Учитывая, что 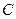 − произвольная постоянная величина, запишем общее решение в виде:
− произвольная постоянная величина, запишем общее решение в виде: 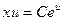 .
.
4). Учитывая что 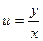 , запишем общее решение уравнения:
, запишем общее решение уравнения: 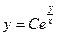 . При
. При 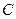 =0 из общего решения получаем также решение
=0 из общего решения получаем также решение  .
.
Ответ: 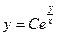 – общее решение (содержит также решение y = 0); также
– общее решение (содержит также решение y = 0); также 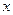 =0.
=0.
Замечание: Каким способом решать Задание 1.3, каждый решает самостоятельно (в зависимости от личных предпочтений). Рекомендация: сравнение Общих схем 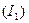 и
и 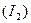 решения Задания вполне очевидно показывает, что схема решения
решения Задания вполне очевидно показывает, что схема решения 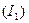 логически проще и менее трудоёмка!..
логически проще и менее трудоёмка!..
Задание 1.3. Решить однородное уравнение:
| Вар. | Уравнение: | Вар. | Уравнение: |
| 1.3.1. | 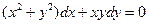
| 1.3.16. | 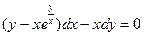
|
| 1.3.2. | 
| 1.3.17. | 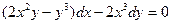
|
| 1.3.3. | 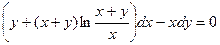
| 1.3.18. | 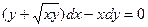
|
| 1.3.4. | 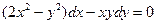
| 1.3.19. | 
|
| 1.3.5. | 
| 1.3.20. | 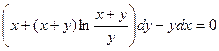
|
| 1.3.6. | 
| 1.3.21. | 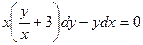
|
| 1.3.7. | 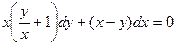
| 1.3.22. | 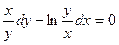
|
| 1.3.8. | 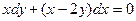
| 1.3.23. | 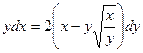
|
| 1.3.9. | 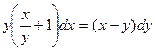
| 1.3.24. | 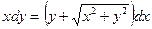
|
| 1.3.10. | 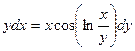
| 1.3.25. | 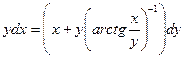
|
| 1.3.11. | 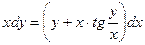
| 1.3.26. | 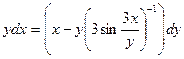
|
| 1.3.12. | 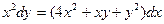
| 1.3.27. | 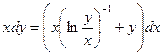
|
| 1.3.13. | 
| 1.3.28. | 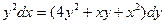
|
| 1.3.14. | 
| 1.3.29. | 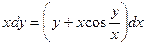
|
| 1.3.15. | 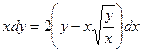
| 1.3.30. | 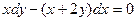
|
1.4. Решить линейное дифференциальное уравнение.
Общие сведения. Для выполнения задания требуется знать, что решить дифференциальное уравнение – это значит найти все его решения. Также важно знать, что линейное дифференциальное уравнение 1-го порядка названо линейным потому, что функции  входят в уравнение в первой степени. Линейные дифференциальные уравнения, как и уравнения с разделяющимися переменными, и однородные уравнения, легко распознаются среди других дифференциальных уравнений и имеют хорошо формализованный алгоритм решения. На первом этапе изучения дифференциальных уравнений это также важно!
входят в уравнение в первой степени. Линейные дифференциальные уравнения, как и уравнения с разделяющимися переменными, и однородные уравнения, легко распознаются среди других дифференциальных уравнений и имеют хорошо формализованный алгоритм решения. На первом этапе изучения дифференциальных уравнений это также важно!
Замечание: Линейное уравнение может быть записано в виде 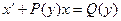 , что только обозначениями отличается от записи:
, что только обозначениями отличается от записи: 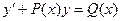 . Общая схема решения уравнения, линейного относительно
. Общая схема решения уравнения, линейного относительно 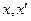 , не отличается от схемы решения, представленной ниже.
, не отличается от схемы решения, представленной ниже.
Задача: Имеем уравнение, приведённое к виду: 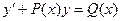 . Необходимо найти все его решения. Если заданы начальные условия, найти частное решение, удовлетворяющее начальным условиям.
. Необходимо найти все его решения. Если заданы начальные условия, найти частное решение, удовлетворяющее начальным условиям.
Сведения из теории линейных уравнений:
1). В теории линейных дифференциальных уравнений 1-го порядка показано, что общая схема решения линейного неоднородного уравнения может быть определена последовательностью действий:
а) найти общее решение однородного уравнения 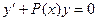 →
→  =
=  ;
;
б) применяя метод вариации произвольной постоянной, записать 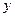 =
= 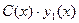 и потребовать, чтобы неизвестная функция
и потребовать, чтобы неизвестная функция 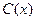 превратила решение
превратила решение  однородного уравнения в решение
однородного уравнения в решение 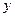 для неоднородного (заданного) уравнения.
для неоднородного (заданного) уравнения.
2). Применение метода вариации произвольной постоянной величины обнаружило формальное требование: сразу искать решение линейного неоднородного дифференциального уравнения в виде функции: 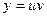 , где
, где 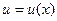 и
и  . Достаточно просто были получены выражения для вычисления функций
. Достаточно просто были получены выражения для вычисления функций  и
и 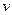 :
:
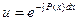 ,
, 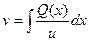 +
+ 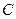 . (1.5)
. (1.5)
3). Общее решение заданного уравнения: 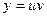 =
= 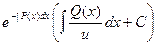 . Указываются также очевидные решения (если такие имеются!), определяемые исходной записью уравнения.
. Указываются также очевидные решения (если такие имеются!), определяемые исходной записью уравнения.
4). Если заданы начальные условия: 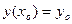 , из общего решения выделяется соответствующее частное решение.
, из общего решения выделяется соответствующее частное решение.
Общая схема решения задачи:
1). В заданном уравнении указываем признаки линейного уравнения и записываем его в стандартной форме: 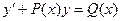 (или
(или 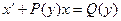 , в соответствии с Заданием).
, в соответствии с Заданием).
2). Принимаем 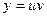 и вычисляем функции
и вычисляем функции 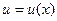 и
и  , применяя формулы (1.5).
, применяя формулы (1.5).
3). Записываем общее решение заданного уравнения: 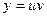 =
= 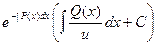 и очевидные решения (если такие имеются!), определяемые исходной записью уравнения.
и очевидные решения (если такие имеются!), определяемые исходной записью уравнения.
4). Если заданы начальные условия: 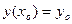 , выделяем из общего решения соответствующее частное решение.
, выделяем из общего решения соответствующее частное решение.
5). Оформляем результат решения задачи – записываем Ответ.
Пример (и образец оформления):
Пример 1.4. Решить дифференциальное уравнение 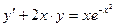 . Найти его частное решение при условии:
. Найти его частное решение при условии:  .
.
Решение:
1). Заданное уравнение линейное относительно  и
и 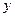 , причём:
, причём: 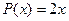 и
и 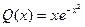 .
.
2). Применяем подстановку: 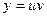 . перепишем заданное уравнение:
. перепишем заданное уравнение: 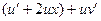 =
=  .
.
3). Вычисляем интеграл: 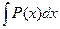 → записываем
→ записываем 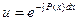 .
.
4). Вычисляем интеграл: 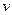 =
= 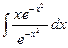 +
+ 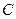 =
= 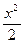 +
+ 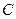 → записываем
→ записываем 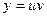 =
= 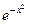 ·
· 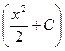 .
.
5). Используя начальные условия (задача Коши), находим: 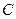 =1 и записываем частное решение уравнения:
=1 и записываем частное решение уравнения: 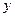 =
= 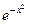 ·
· 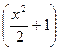 .
.
Ответ: 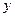 =
= 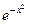 ·
· 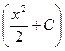 – общее решение; частное решение уравнения:
– общее решение; частное решение уравнения: 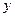 =
= 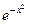 ·
· 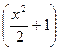 .
.
Замечание. В задании (1.4) используются линейные уравнения как относительно  , так и относительно
, так и относительно  . Для первого случая начальные условия представлены в виде:
. Для первого случая начальные условия представлены в виде: 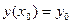 , для второго случая в виде:
, для второго случая в виде: 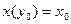 .
.
Задание 1.4. Решить линейное дифференциальное уравнение и найти частное решение для заданных начальных условий:
| Вар. | Уравнение и начальные условия: | Вар. | Уравнение и начальные условия: |
| 1.4.1. | 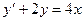 , ,  . .
| 1.4.16. | 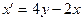 , , 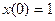 . .
|
| 1.4.2. | 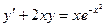 , ,  . .
| 1.4.17. | 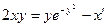 , , 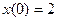 . .
|
| 1.4.3. | 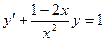 , ,  . .
| 1.4.18. | 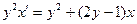 , , 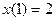 . .
|
| 1.4.4. | 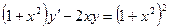 , ,  . .
| 1.4.19. | 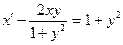 , , 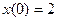 . .
|
| 1.4.5. |  , ,  . .
| 1.4.20. | 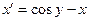 , , 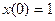 . .
|
| 1.4.6. | 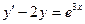 , , 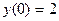 . .
| 1.4.21. | 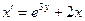 , , 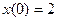 . .
|
| 1.4.7. | 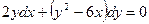 , ,  . .
| 1.4.22. | 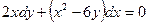 , , 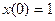 . .
|
| 1.4.8. | 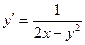 , , 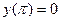 . .
| 1.4.23. |  , , 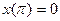 . .
|
| 1.4.9. |  , , 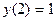 . .
| 1.4.24. | 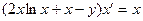 , , 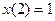 . .
|
| 1.4.10. | 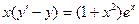 , , 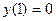 . .
| 1.4.25. | 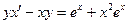 , ,  . .
|
| 1.4.11. | 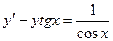 , , 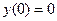 . .
| 1.4.26. | 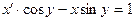 , , 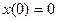 . .
|
| 1.4.12. | 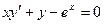 , , 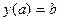 . .
| 1.4.27. | 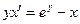 , ,  . .
|
| 1.4.13. | 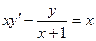 , , 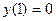 . .
| 1.4.28. | 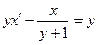 , ,  . .
|
| 1.4.14. |  , , 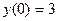 . .
| 1.4.29. |  , , 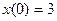 . .
|
| 1.4.15. | 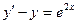 , , 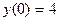 . .
| 1.4.30. | 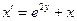 , ,  . .
|
1.5. Решить дифференциальное уравнение Бернулли.
Общие сведения. Для выполнения задания требуется знать, что решить дифференциальное уравнение – это значит найти все его решения. Также важно знать, что уравнение Бернулли отличается от линейного дифференциального уравнения 1-го порядка только множителем 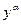 в его правой части, причём необходимо
в его правой части, причём необходимо 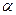 не равно 0 и 1, так как при этих значениях уравнение Бернулли превращается в линейное уравнение. Заметим, что для случаев
не равно 0 и 1, так как при этих значениях уравнение Бернулли превращается в линейное уравнение. Заметим, что для случаев 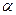 >0 сразу выделяется одно из решений уравнения:
>0 сразу выделяется одно из решений уравнения: 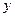 =0.
=0.
Задача: Имеем уравнение, приведённое к виду: 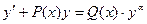 . Необходимо найти все его решения. Если заданы начальные условия, найти частное решение, удовлетворяющее начальным условиям.
. Необходимо найти все его решения. Если заданы начальные условия, найти частное решение, удовлетворяющее начальным условиям.
Общая схема решения задачи:
1). Убедившись, что заданное уравнение есть уравнение Бернулли, при помощи подстановки 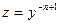 преобразуем его в линейное уравнение:
преобразуем его в линейное уравнение:
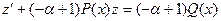 , или:
, или: 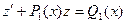 . (1.6)
. (1.6)
2). Применив стандартный алгоритм решения линейного уравнения, находят функцию 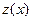 . Учитывая использованную подстановку, записывают решение исходного уравнения. При оформлении решения, в случае
. Учитывая использованную подстановку, записывают решение исходного уравнения. При оформлении решения, в случае 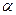 >0 учитывают также решение:
>0 учитывают также решение: 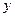 =0.
=0.
3). Если заданы начальные условия: 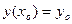 , выделяем из общего решения соответствующее частное решение.
, выделяем из общего решения соответствующее частное решение.
4). Оформляем результат решения задачи – записываем Ответ.
Пример (и образец оформления):
Пример 1.5. Решить дифференциальное уравнение Бернулли:  ∙
∙ 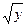 .
.
Решение:
1). Заданное дифференциальное уравнение есть уравнение Бернулли, для случая 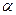 =
= 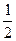 , одним из решений которого есть
, одним из решений которого есть  .
.
2). Применяя подстановку 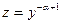 =
=  , получаем линейное дифференциальное уравнение:
, получаем линейное дифференциальное уравнение: 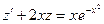 , где
, где 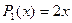 и
и 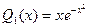 . Решение ищем в виде:
. Решение ищем в виде: 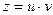 .
.
2). Применим подстановку: 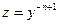 =
=  , перепишем заданное уравнение по общей формуле:
, перепишем заданное уравнение по общей формуле: 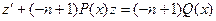 , то есть в форме:
, то есть в форме: 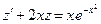 , или
, или  , где
, где 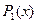 =
= 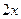 ,
, 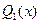 =
= 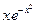 .
.
3). Далее применяем стандартный алгоритм решения линейного уравнения: 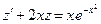 , записанного в стандартной форме, приняв
, записанного в стандартной форме, приняв 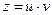 .
.
4). Вычисляем интеграл: 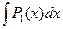 =
= 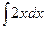 =
= 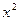 и записываем выражение:
и записываем выражение: 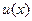 =
= 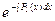 =
=  .
.
5). Вычисляем: 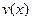 =
= 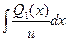 +
+ 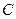 =
= 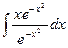 +
+ 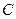 =
= 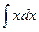 =
= 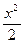 +
+ 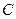 .
.
6). Запишем общее решение уравнения: 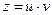 =
= 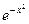 ∙
∙  , или
, или  =
= 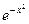 ∙
∙  .
.
Ответ:  =
= 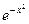 ∙
∙  – общее решение, также решение
– общее решение, также решение  .
.
Задание 1.5. Решить уравнение Бернулли:
| Вар. | Уравнение: | Вар. | Уравнение: | ||||||
| 1.5.1. | 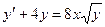 . .
| 1.5.16. |  . .
| ||||||
| 1.5.2. | 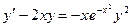 . .
| 1.5.17. |  . .
| ||||||
| 1.5.3. | 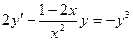 . .
| 1.5.18. | 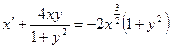 . .
| ||||||
| 1.5.4. | 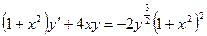 . .
| 1.5.19. | 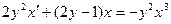 . .
| ||||||
| 1.5.5. | 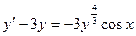 . .
| 1.5.20. |  . .
| ||||||
| 1.5.6. | 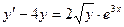 . .
| 1.5.21. | 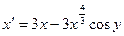 . .
| ||||||
| 1.5.7. | 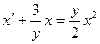 . .
| 1.5.22. |
Дата добавления: 2014-10-14; просмотров: 508; Нарушение авторских прав 
Мы поможем в написании ваших работ! |