Основные теоретические положения. Рассмотрим электрическую цепь приемников электроэнергии синусоидального тока, которая состоит из параллельно соединенных реальных катушки индуктивности L и

Рассмотрим электрическую цепь приемников электроэнергии синусоидального тока, которая состоит из параллельно соединенных реальных катушки индуктивности L и конденсатора С(рис. 4.1). Реально в их состав входят и активные сопротивления, определяющие потери энергии в катушке и токи утечки конденсатора, что учтем включением последовательно с реактивными элементами и соответствующих активных сопротивлений R₁ и R₂.

Рис. 4.1. Параллельное соединение реальных

катушки индуктивности и конденсатора

Обе параллельные ветви цепи находятся под одним синусоидальным напряжением U, токи в них I₁ и I₂ равны:

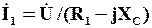, (4.1)

. (4.2)

Комплексный ток I, потребляемый всей цепью, можно определить по первому закону Кирхгофа:

(4.3)

Подставляя значения токов и проведя преобразования, получим:

. (4.4)

Откуда можно записать величины активных и реактивных проводимостей первой и второй ветвей цепи:

g₁= , g₂ = ; b_C= , b_L= . (4.5).

С учетом введенных обозначений выражение (4.4) можно записать в виде

[(g₁+g₂)+j(b_C–b_L)]. (4.6)

Выражение

y_Э=(g₁+g₂)+j(b_C–b_L). (4.7)

называется эквивалентной полной комплексной проводимостьюразветвленной цепи синусоидального тока. Модуль этой величины называется полной проводимостью. Полная проводимость определяться выражением

y_Э= . (4.8)

На основании (4.6) и (4.7) модуль комплексного тока будет

I=U . (4.9)

Особый интерес представляет случай, когда емкостная и индуктивная проводимости равны друг другу:

b_с=b_L.(4.10)

Этот режим работы разветвленной цепи из параллельного соединения катушки индуктивности и конденсатора, характеризующийся равенством индуктивной и емкостной проводимостей, называется резонансом тока. При резонансе реактивные мощности индуктивности и конденсатора взаимно компенсируют друг друга, поэтому цепь потребляет только активную мощность. Ток, потребляемый от источника, содержит только активную составляющую I=U(g₁+g₂) и имеет минимальное значение. Так как реактивные проводимости взаимно компенсируются, то полная проводимость равна активной проводимости y_э=g_э, а коэффициент мощности равен единице:

cosφ= = 1. (4.11)

Для этого режима ток, потребляемый цепью, часто оказывается значительно меньше токов, протекающих через реактивные элементы:

I_L=I_C>I. (4.12)

Активная мощность в цепи при резонансе

P=Ucosφ=UI=S. (4.13)

Реактивная мощность всей цепи равна нулю, хотя мощность на каждом реактивном элементе может оказаться весьма значительной:

Q=Q_L–Q_C=U²(b_L–b_C)=0. (4.14)

В режиме резонанса токов рассматриваемая цепь ведет себя по отношению к источнику питания так, как будто она состоит из элемента с активной проводимостью.

Учитывая, что промышленные потребители электрической энергии в основном носят активно-индуктивный характер, их можно представить в виде эквивалентной схемы из последовательно соединенных R_при X_Lпр(рис. 4.2,а).

При отсутствии емкости С(рис. 4.2,а) ток в линии электропередачи

. (4.15)

а) б)

Рис. 4.2. Принцип компенсации реактивной мощности конденсатором:

а) схема; б) векторная диаграмма токов

Мощность потерь в линии будет равна

. (4.16)

Для снижения мощности потерь в линии при постоянстве потребляемой приемником активной мощности Р_пр≈constи напряжения сети U=constнеобходимо уменьшить угол φ₁между током I_Lи напряжением U до приемлемого значения. Для этого можно включить параллельно приемнику конденсатор С. На векторной диаграмме рис. 4.2,б показано, что при этом фазовый сдвиг между напряжением в линии и током в ней уменьшается до величины φ₂ и величина тока в линии приближается к величине активной составляющей тока приемника I_прА. Реактивная мощность приемника Q₁=P_прtgφ₁компенсируется емкостной реактивной мощностью конденсатора до величины Q₂=P_прtgφ₂. Компенсирующая мощность конденсатора равна разности реактивных мощностей в линии до и после включения конденсатора:

Q_C=Q₁–Q₂=P_пр(tgφ₁–tgφ₂). (4.17)

Реактивная мощность конденсата связана с величиной его емкости Ссоотношением:

Q_C=2πfCU², (4.18)

где f – частота тока сети.

Из (4.17) и (4.18) можно определить необходимое значение емкости конденсатора:

C=P_пр(tgφ₁–tgφ₂)/(2πfCU²). (4.19)

Для полной компенсации реактивной мощности необходимо получить фазовый сдвиг φ₂=0 Для этого требуется конденсатор емкостью

C=P_пр(tgφ₁)/(2πfCU²). (4.20)

Дата добавления: 2014-10-14; просмотров: 225; Нарушение авторских прав

Мы поможем в написании ваших работ!