
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лабораторная работа №1
Экспериментальное определение статических и динамических характеристик объекта регулирования.
Цель работы: Освоение методики экспериментального получения статических характеристик и кривых разгона и их обработки для получения передаточных функций и частотных характеристик объектов регулирования.
Описание лабораторного стенда.
Физическая модель объекта регулирования выполнена в виде трубчатой электрической печи 1 (рис. 1). Внизу расположен вентилятор 2, а также заслонка 3 с указателем угла поворота 4, выполняющая роль регулирующего органа системы. Выходная координата теплового объекта – температура в печи – измеряется термопарой 5, подключенной к электронному потенциометру 6. Напряжение питания электрической печи – входная координата объекта – может быть изменена автотрансформатором 7 и контролируется вольтметром 8, ток в цепи – амперметром на панели стенда. Вторая входная координата объекта – положение заслонки 3 – регулирующего органа системы. Таким образом, в объекте имеется два канала передачи воздействий: напряжения питания Х I температура в печи; положения заслонки Х II температура в печи.
| V |
Х I
Х II У
Рис.1 Объект регулирования и его структурная схема.
Задание.
1. Освоить способ нанесения входного возмещения в виде ступенчатых функций.
2. Нанести входные ступенчатые возмущения по исследуемым каналам и записать соответствующие кривые разгона на диаграмме измерительного прибора.
3. Получить дифференциальное уравнение объекта.
4. Получить передаточную функцию объекта и построить частотные характеристики по исследуемому каналу.
5. По данным об установившихся значениях выходной величины, полученных при различных возмущениях на одном стенде, построить статическую характеристику.
Основные положения.
Статические и динамические характеристики объекта регулирования необходимо знать для правильной разработки автоматической системы регулирования, для расчета настроек автоматического регулятора, обеспечивающих выполнение заданных требований по устойчивости и качеству процессов регулирования в системе.
Статическая характеристика объекта регулирования – зависимость выходной его координаты от входной в установившихся режимах. Статическая характеристика может быть получена экспериментально по следующей методике: при установившемся режиме в объекте (при этом значения входной координаты x1, выходной y1(t)=const) на входе объекта устанавливают новое значение входной координаты x2 и по окончании переходного процесса на выходе объекта записывают новое установившиеся значение выходной координаты y2. Повторяют эксперимент при x3, получают y3 и т.д. Результаты экспериментов заносят в таблицу1, по данным которой строят графики y(x).
Таблица 1
| x |
| ||
| x1 x2 x3 … | y1 y2 y3 … |
Статистическая характеристика чаще получается не линейной и требует линеаризации.
Динамические характеристики объекта могут быть получены в удобной для расчета форме путем обработки экспериментальных кривых разгона (переходных функций) объекта. В общем случае кривые разгона получают как по каналу регулирования, так и по каналам возмущающих воздействий. В настоящей работе необходимо получить кривую разгона по каналу «напряжение питания печи – температура печи».
При экспериментальном определении динамических характеристик объектов рекомендуется получать кривые разгона, нанося ступенчатое входное воздействие один раз в сторону увеличения входной координаты, другой раз – в сторону ее уменьшения. Считают, что совпадение полученных характеристики по одному и тому же каналу обеспечивает достоверность результатов.
Величина ступенчатого входного воздействия в общем случае составляет 10 – 15% от номинального значения входной величины.
Определение дифференциального уравнения объекта по его кривой разгона (метод интегральных площадей).
На рис. 2 показан участок диаграммной бумаги с графиком кривой разгона, полученной в результате внесения ступенчатого возмущения в виде изменения напряжения питания на величину А (Вольт).
Обработку графика начинают с установления времени чистого запаздывания τ, то есть времени от момента нанесения возмущения до момента «отрыва» кривой разгона от линии исходного состояния равновесия.
На линии исходного состояния равновесия проводят ось времени t, на которой отмечают выбранные интервалы времени с учетом скорости движения диаграммы. При этом за начало отсчета принимают момент окончания времени чистого запаздывания.
Рекомендуется принять от 8 до 12 интервалов разбиения оси времени от окончания запаздывания до момента, когда можно считать переходный процесс закончившимся (постоянное значение температуры).
| Дата: Студент: Скорость диаграммы: |
| Стенд № |
| t, c |
| ∆θ∞-∆θ |
| τ |
| θ0 |
| θ |
| ∆θ |
| 0 30 60 |
| Момент нанесения возмущения |
Рис. 2. Участок диаграммной бумаги с графиком кривой разгона
Далее обработку экспериментальных данных удобно вести, заполняя табл. 2. Пользуясь графиком, заполняют столбцы 1, 2 таблицы. Заполняют столбец 3, принимая, таким образом, за начало отсчета выходной величины ее значение θ0 в момент нанесения возмущения. Для перехода от кривой разгона к переходной функции объекта ординаты кривой разгона (столбец 3) делят на величину возмущения А (Вольт), заполняют таким образом столбец 4.
Таблица 2.
| t, мин | θ, °С | ∆θ= =θ-θ0 | 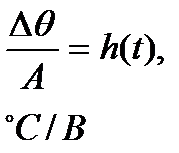
|
| 0,5 … |
По данным столбцов 1 и 4 строят (с учетом времени чистого запаздывания) график переходной функции (рис. 3), по нему определяют коэффициент усиления объекта К.
| τ |
| к |
| t |
| h |
| t |
| x |
Рис. 3 График переходной функции объекта.
Получение математического описания объекта на ЭВМ.
Расчеты производятся на ЭВМ в программе TAU. Программа предназначена для расчета АСР, в настоящей работе выполняется только: этап 1 – расчет коэффициентов дифференциального уравнения;
этап 2 – проверка правильности аппроксимации;
этап 3 – расчет частотных характеристик объекта.
Дифференциальное уравнение объекта записывается в виде
a3y,,,(t)+ a2y,,(t)+ a1y,(t)+ y (t)=Kx(t- τ)
где K, τ – коэффициент усиления и запаздывание объекта (см. рис. 3)
При использовании этапа 1 следует ввести требуемые исходные данные: интервал разбиения оси абсцисс кривой разгона 0,5 максимальное установившиеся значения по кривой разгона (к рис. 3) число точек (необходимо учесть точку при t=0).
Результат расчета: коэффициенты дифференциального уравнения объекта
а1=
а2=
а3=
При использовании этапа 2 на ЭВМ производится решение дифференциального уравнения объекта, результаты выводятся в виде таблицы, по данным которой следует построить графики экспериментальной и расчетной переходных функций для их сравнения.
При использовании этапа 3 следует ввести исходные данные.
Степень колебательности 0
Передаточный коэффициент объекта (коэффициент усиления К)
Время запаздывания (τ с графика рис. 2)
Начальные и конечные значения частоты – можно ввести нули, ЭВМ определит необходимый диапазон и рассчитает частотные характеристики при изменении фазы от 90 до 1800.
| M K |
| ωcр ω |
| ω |
| φ |
| ∞ ω |
| W (iω) |
| iIm |
| Re |
| K(ω=0) |
| φ(ω) |
| M(ω) |
Рис. 4. Частотные характеристики объекта
| <== предыдущая страница | | | следующая страница ==> |
| Заключения о проделанной работе | | | Порядок выполнения работы. Снятие кривой разгона проводится индивидуально каждым студентом |
Дата добавления: 2014-10-17; просмотров: 465; Нарушение авторских прав

Мы поможем в написании ваших работ!