
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ПРАКТИЧЕСКАЯ РАБОТА № 1-2
Системы счисления. Преобразование чисел в различных системах счисления.
1.Цель работы: Выработать умение преобразовывать числа из одной позиционной системы счисления в другую. Научиться пользоваться таблицей кодов чисел в различных системах счисления для преобразования чисел из одной системы счисления в другую.
2.Краткие теоретические сведения. Под системой счисления понимается способ представления любого числа с помощью ограниченного алфавита символов, называемых цифрами. Различают позиционные и непозиционные системы счисления. В информатике применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную и шестнадцатеричную. Преобразование числа из одной позиционной системы в другую осуществляется по одному из следующих правил: замещение, деление, умножение или деление-умножение. Правило замещения реализуется при переводе чисел из недесятичной системы счисления в десятичную на основе формулы: 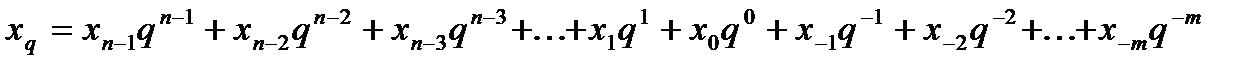 ; а также при переводе из двоичной системы в восьмеричную и обратно, при переводе из двоичной системы в шестнадцатеричную и обратно с использованием таблицы кодов. Правило деления используется при преобразовании целых чисел. Правило умножения реализуется при переводе правильных дробей. Правило деление-умножение используют при преобразовании смешанных чисел.
; а также при переводе из двоичной системы в восьмеричную и обратно, при переводе из двоичной системы в шестнадцатеричную и обратно с использованием таблицы кодов. Правило деления используется при преобразовании целых чисел. Правило умножения реализуется при переводе правильных дробей. Правило деление-умножение используют при преобразовании смешанных чисел.
Таблица кодов чисел в различных системах счисления.
| x10 | |||||||||
| x2 | |||||||||
| x8 | |||||||||
| x16 | |||||||||
| x10 | |||||||||
| x2 | |||||||||
| x8 | |||||||||
| x16 | A | B | C | D | E | F |
3. Задания:
1. Числа, записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 1)1210; 2)16528; 3)11012; 4)АВ916; 5)0,27048; 6)324410; 7)327548; 8)110012; 9)Е3В5D16; 10)271,378.
2. Числа записанные в виде полинома разложения, представить в свернутой форме и подсчитать значение числа в десятичной системе счисления: 1)5*103+0*102+3*101+8*100; 2)3*8-1+5*8-2+6*8-3+2*8-4;
3)1*24+1*23+0*22+0*21+0*20; 4)А*16-2+В*16-3+9*16-4+Е*16-5+С*16-6;
5)7*163+0*162+С*161+Е*160+2*16-1+4*16-2.
3. Перевести из восьмеричной системы счисления в двоичную.
1)74; 2)541; 3)6001; 4)52311; 5)554421; 6)0,742; 7)0,541; 8)0,1006; 9)0,52311; 10)0,445512.
4. Перевести из шестнадцатеричной системы счисления в двоичную.
1)А0; 2)4Е5; 3)3405; 4)5А6В0; 5)39АСВ; 6) 0,АВ; 7)0,4B5; 8)0,4305; 10)0,А76В1; 11)0,39АС3; 11)1,В; 12)39,B2; 13)5А8,В3; 14)717,00В; 15)10С2,А01.
5. Перевести из десятичной системы счисления в двоичную.
1)256; 2)1000; 3)2304; 4)8192; 5)13323; 6)0,257; 7)0,1025; 8)0,4622; 9)0,7351; 10)0,27456; 11)33,1; 12)100,4; 13)921,7; 14)29,6791; 15)99,9999.
6. Перевести из десятичной системы счисления в восьмеричную.
1) 133; 2)4096; 3)16449; 4)30001; 5)43675.
7. Перевести из десятичной системы счисления в шестнадцатеричную.
1)266; 2)8192; 3)32898; 4)60002; 5)87350.
8. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную.
1)0,101101; 2)0,111100; 3)0,11011011; 4)0,11110011; 5)0,0101101010; 6)11,01011; 7)1101,110001; 8)11010,0011011; 9)10111,0000101; 10)110111,1110101.
9. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную.
1)0,777; 2)0,1327; 3)0,0073; 4)0,66321; 5)0,852601; 6)28,75; 7)425,777; 8)1937,998; 9)29,397; 10)937,739.
4. Домашнее задание:
Вариант 1.
1. Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 4802510
2. Перевести из восьмеричной системы счисления в двоичную: 203.
3. Перевести из шестнадцатеричной системы счисления в двоичную: D3Е.
4. Перевести из десятичной системы счисления в двоичную: 691.
5. Перевести из десятичной системы счисления в восьмеричную: 1020.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 2041.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 0,110111.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 0,0951.
Вариант 2.
1. Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 1037658
2. Перевести из восьмеричной системы счисления в двоичную.0,1467;
3. Перевести из шестнадцатеричной системы счисления в двоичную: 0,9D2А.
4. Перевести из десятичной системы счисления в двоичную: 0,4001.
5. Перевести из десятичной системы счисления в восьмеричную:5078.
6. Перевести из десятичной системы счисления в шестнадцатеричную.2451.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 101,101110.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 102,137.
Вариант 3.
1. Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 76,458
2. Перевести из восьмеричной системы счисления в двоичную.0,1467;
3. Перевести из шестнадцатеричной системы счисления в двоичную: 0,9D2А.
4. Перевести из десятичной системы счисления в двоичную: 0,4001.
5. Перевести из десятичной системы счисления в восьмеричную:5078.
6. Перевести из десятичной системы счисления в шестнадцатеричную.2451.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 101,101110.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 102,137.
Вариант 4.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 1011,1012.
2. Перевести из восьмеричной системы счисления в двоичную.0,5432;
3. Перевести из шестнадцатеричной системы счисления в двоичную: 0,E54C.
4. Перевести из десятичной системы счисления в двоичную: 0,408.
5. Перевести из десятичной системы счисления в восьмеричную:6996.
6. Перевести из десятичной системы счисления в шестнадцатеричную.7432.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 0.110011.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 56,942.
Вариант 5.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 10101,012.
2. Перевести из восьмеричной системы счисления в двоичную.7,44;
3. Перевести из шестнадцатеричной системы счисления в двоичную: 8,DC.
4. Перевести из десятичной системы счисления в двоичную: 12,78.
5. Перевести из десятичной системы счисления в восьмеричную:96,115.
6. Перевести из десятичной системы счисления в шестнадцатеричную.6,725.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 1011,01.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 0,287.
Вариант 6.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 15С,В316.
2. Перевести из восьмеричной системы счисления в двоичную 7711.
3. Перевести из шестнадцатеричной системы счисления в двоичную: 4C,09А.
4. Перевести из десятичной системы счисления в двоичную: 9,045.
5. Перевести из десятичной системы счисления в восьмеричную: 0,497.
6. Перевести из десятичной системы счисления в шестнадцатеричную 88445.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 11,10111.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 29,765.
Вариант 7.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 10011,112.
2. Перевести из восьмеричной системы счисления в двоичную 76332;
3. Перевести из шестнадцатеричной системы счисления в двоичную: CАА6.
4. Перевести из десятичной системы счисления в двоичную: 9675.
5. Перевести из десятичной системы счисления в восьмеричную: 0,327.
6. Перевести из десятичной системы счисления в шестнадцатеричную. 0,778.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 110,1011.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 34,654.
Вариант 8.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 360,0578.
2. Перевести из восьмеричной системы счисления в двоичную 60,606;
3. Перевести из шестнадцатеричной системы счисления в двоичную: А,95С.
4. Перевести из десятичной системы счисления в двоичную: 0,234.
5. Перевести из десятичной системы счисления в восьмеричную: 5599.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 0,547.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 1001,11.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 77,78.
Вариант 9.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 90В,0А16.
2. Перевести из восьмеричной системы счисления в двоичную: 44,77;
3. Перевести из шестнадцатеричной системы счисления в двоичную: C,67.
4. Перевести из десятичной системы счисления в двоичную: 5544.
5. Перевести из десятичной системы счисления в восьмеричную: 0,445.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 55343.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 101,111111.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 12,2378.
Вариант 10.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 1001,11012.
2. Перевести из восьмеричной системы счисления в двоичную: 0,2323;
3. Перевести из шестнадцатеричной системы счисления в двоичную: А9А,9.
4. Перевести из десятичной системы счисления в двоичную: 234,432.
5. Перевести из десятичной системы счисления в восьмеричную: 4422.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 0,879.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 11,011.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 222,222.
Вариант 11.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 2367,018.
2. Перевести из восьмеричной системы счисления в двоичную: 27,65;
3. Перевести из шестнадцатеричной системы счисления в двоичную: 0,65С.
4. Перевести из десятичной системы счисления в двоичную: 4083.
5. Перевести из десятичной системы счисления в восьмеричную: 7959.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 9999.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 10,101.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 99,99.
Варант12.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: С09,09С16.
2. Перевести из восьмеричной системы счисления в двоичную: 44,54;
3. Перевести из шестнадцатеричной системы счисления в двоичную: АС0,8E5.
4. Перевести из десятичной системы счисления в двоичную: 777.
5. Перевести из десятичной системы счисления в восьмеричную: 669.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 0,7662.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 111,111.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 111,999.
Вариант 13.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 1010,0012.
2. Перевести из восьмеричной системы счисления в двоичную: 0,775;
3. Перевести из шестнадцатеричной системы счисления в двоичную: 45,EC.
4. Перевести из десятичной системы счисления в двоичную: 0,894.
5. Перевести из десятичной системы счисления в восьмеричную: 2003.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 2002.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 1000,011.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 2002,03.
Вариант 14.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: 0,7828.
2. Перевести из восьмеричной системы счисления в двоичную: 2,807.
3. Перевести из шестнадцатеричной системы счисления в двоичную: 99,СС.
4. Перевести из десятичной системы счисления в двоичную: 45,45.
5. Перевести из десятичной системы счисления в восьмеричную: 21111.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 790,7.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 10011,0001.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 76,6677.
Вариант 15.
1.Числа записанные в свернутой форме, представить в виде полинома разложения и подсчитать значение числа в десятичной системе счисления: С09А,08В16.
2. Перевести из восьмеричной системы счисления в двоичную: 0,5976;
3. Перевести из шестнадцатеричной системы счисления в двоичную: E5,04C.
4. Перевести из десятичной системы счисления в двоичную: 8909.
5. Перевести из десятичной системы счисления в восьмеричную: 0,69.
6. Перевести из десятичной системы счисления в шестнадцатеричную: 7272.
7. Перевести из двоичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 11,00111101.
8. Перевести из десятичной системы счисления в: а) восьмеричную; б)шестнадцатеричную: 666,999.
5. Содержание отчета:
5.1. Тема практической работы.
5.2.Цель работы.
5.3. Задание.
5.4.Решение задач.
5.5.Ответы на контрольные вопросы.
6. Контрольные вопросы:
1. Что такое система счисления?
2.Дать определение понятию основание.
3.Чем отличается позиционная система счисления от непозиционной?
4.Какие системы счисления используются в информатике?
5.Сколько цифр используется для записи чисел в двоичной системе, восьмеричной системе, шестнадцатеричной системе?
6.По каким правилам происходит преобразование чисел из одной системы в другую?
7.Когда используются эти правила?
8.Сформулировать правило деления.
9.сформулировать правило умножения.
7. Литература:
1. Наймин В.А., Питеркин В.М., Уртминцев А.Г. “Информатика. Пособие по углубленному изучению информатики для учащихся средней школы и поступающих в технические университеты.”
2.Хомоненко. “Основы современных компьютерных технологий.”
3.Зайцев В.Ф. “Кодирование информации в ЕС ЭВМ”.
| <== предыдущая страница | | | следующая страница ==> |
| Семинар - 2 часа. 1. Общая характеристика уголовного процесса развитых зарубежных государств | | | ПРАКТИЧЕСКАЯ РАБОТА №3 |
Дата добавления: 2014-10-17; просмотров: 695; Нарушение авторских прав

Мы поможем в написании ваших работ!