
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Однофакторный эксперимент
При использовании метода однофакторного экспериментирования все факторы, кроме одного стабилизируются на одном уровне. При планировании однофакторного эксперимента исследователь определяет необходимый объем данных, структуру модели и осуществляет проверку ее адекватности.
Уравнение математической регрессии целевой функции при однофакторном эксперименте принимает вид у = f ( х ). Нахождение вида функциональной зависимости основывается на методе максимального правдоподобия.
Метод максимального подобия предписывает выбирать неизвестные коэффициенты таким образом, чтобы функцию правдоподобия случайного вектора x1, ...., xn была максимальна. Предусматривается, что вектор ошибок состоит из неизвестных и одинаково распределенных случайных величин, имеющих нормальный закон распределения.
Функция правдоподобия имеет вид:
|
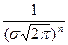 exp { -
exp { - 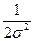
 ( yi –f (xi)2 }
( yi –f (xi)2 }
При любом фиксированном значении дисперсии σ2 максимум функции правдоподобия достигается при наименьшем значении суммы квадратов ошибок (невязок) эксперимента. Значение ошибки в предсказании влияния фактора на процесс по найденному уравнению результата определяется как разность предсказанного значения (вычисленного по найденному уравнению) выхода процесса и полученного в этом опыте значения выхода процесса.
|
На практике обработку результатов эксперимента проводят методом наименьших квадратов.
Предположим, что исследуемый процесс описывается линейным уравнением : y=bo+ b1x.
В соответствии с методом наименьших квадратов функция Ф должна быть минимальна.
|
 ( ŷi – yi )2=
( ŷi – yi )2=  [( bo + b1 xi ) – yi ]2=
[( bo + b1 xi ) – yi ]2=
=  (bo2 + 2 b0b1xi + b1 2xi2 – 2 b0 yi – 2 b1 xi yi +yi 2)
(bo2 + 2 b0b1xi + b1 2xi2 – 2 b0 yi – 2 b1 xi yi +yi 2)
Уравнение в частных производных выглядит следующим образом:
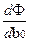 =
=  (2bo + 2b1xi – 2 yi ) =0
(2bo + 2b1xi – 2 yi ) =0
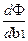 =
=  ( 2boxi + 2 b1 xi2 – 2 xi yi ) =0.
( 2boxi + 2 b1 xi2 – 2 xi yi ) =0. 
Имеем систему уравнений :
|
 yi = bo
yi = bo  1+ b1
1+ b1  xi2
xi2
 xi yi= bo
xi yi= bo  xi+ b1
xi+ b1  xi2
xi2
Решение системы уравнений имеет вид:
 yi yi  xi2 – xi2 –  xi xi  xi yi xi yi
| ||||
N  xi2 – ( xi2 – (  xi) 2 xi) 2
|
 xi yi – xi yi –  yi yi  xi xi
| ||||
N  xi2 – ( xi2 – (  xi) 2 xi) 2
|
При обработке результатов однофакторных экспериментов с целью получения уравнения регрессии второй степени y=bo+ b1x + b2x2 необходимо будет минимизировать функцию вида:
Ф =  ( ŷi – yi )2=
( ŷi – yi )2=  [( bo + b1 xi + b2xi 2) – yi ]2=
[( bo + b1 xi + b2xi 2) – yi ]2=
|
 (bo2 + 2 bob1xi + b1 2xi2 + 2 bo b2xi2 – 2 bo yi + 2 b1 b2 xi 3 – 2 b1 xi yi +
(bo2 + 2 bob1xi + b1 2xi2 + 2 bo b2xi2 – 2 bo yi + 2 b1 b2 xi 3 – 2 b1 xi yi +
+b2 2xi4 – 2 b2 xi 2yi +yi 2)
Нахождение коэффициентов уравнения сводится к решению системы:
|
 ( bo+ b1xi + b2 xi 2– yi) =0
( bo+ b1xi + b2 xi 2– yi) =0
 ( bo+ b1xi + b2 xi 2– yi) xi =0
( bo+ b1xi + b2 xi 2– yi) xi =0
 ( bo+ b1xi + b2 xi 2– yi) xi 2=0
( bo+ b1xi + b2 xi 2– yi) xi 2=0
При нахождении коэффициентов уравнения третьей степени
y = bo+ b1x + b2x2+ b3x3. Представленная выше система уравнений дополнится уравнением  ( bo+ b1xi + b2 xi 2+ b3 xi 3– yi) xi 3 = 0.
( bo+ b1xi + b2 xi 2+ b3 xi 3– yi) xi 3 = 0.
Решение систем уравнений значительно упрощается, если при планировании эксперимента будет обеспечено равенство  xi = 0. В этом случае коэффициенты линейного уравнения определяются по формуле:
xi = 0. В этом случае коэффициенты линейного уравнения определяются по формуле:
 yi yi
| ||||
| ||||
 xi yi xi yi
| ||||
 xi2 xi2
|
Коэффициенты квадратичного уравнения определяются по формулам:
 (yi – b2 xi2 ) (yi – b2 xi2 )
| |||||
| N | |||||
 xi yi xi yi
| |||||
 xi2 xi2
| |||||
 (yi – bo ) xi2 (yi – bo ) xi2
| |||||
 xi4 xi4
|
При обработке результатов эксперимента часто пользуются графическим методом. Построение графиков позволяет наглядно изображать полученные зависимости, дает возможность производить графическим путем интерполяцию.
При построении графика масштаб на осях следует выбирать так, чтобы кривая не растягивалась вдоль одной из осей, а лежала по возможности ближе к биссектрисе координатного угла. Кривая проводится через нанесенные на миллиметровой бумаге точки плавно, без резких искривлений. Кривая должна охватывать как можно больше точек и проходить между ними так, чтобы по обе стороны от нее точки располагались равномерно.
Если измерения величины X проводились точнее, чем величины Y, то на графике вместо точек наносятся штрихи, длина которых соответствует точности измерений. Если на графике учитывается точность определения как величины X, так и Y, то штрихи заменяются четырехугольниками погрешностей. Кривая проводится плавно, по возможности через центры штрихов или прямоугольников.
Условия оптимального ведения процесса будет равенство Х=Хopt

|

|
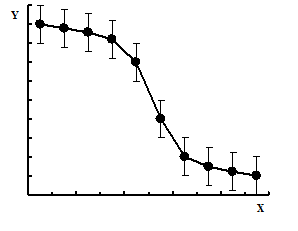
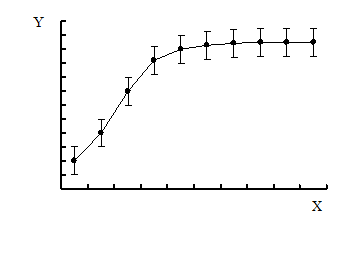
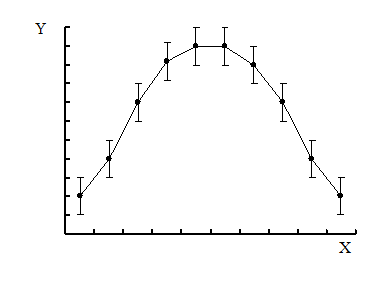
Рис.3 Графики однофакторного эксперимента.
Основные положения планирования многофакторного эксперимента
Для исследования влияния на процесс двух факторов необходимо провести эксперимент при различных сочетаниях изучаемых факторов.
Допустим, что зависимость факторов описывается линейным уравнением вида y=bo+ b1x1 + b2x2.
Для нахождения коэффициентов уравнения из условия :
|
 ( ŷi – yi )2=
( ŷi – yi )2=  [( bo + b1 x1 + b2x2 ) – yi ]2 → min
[( bo + b1 x1 + b2x2 ) – yi ]2 → min
Необходимо решить систему уравнений
|
 ( bo + b1x1i + b2 x2i ) =
( bo + b1x1i + b2 x2i ) =  yi
yi
 ( bo x1i + b1x1i 2+ b2 x1i x2i ) =
( bo x1i + b1x1i 2+ b2 x1i x2i ) =  x1i yi
x1i yi
 ( bo x2i + b1 x1i x2i + b2 x2i 2 ) =
( bo x2i + b1 x1i x2i + b2 x2i 2 ) =  x2i yi
x2i yi
Решение системы уравнений значительно упростится при переходе от натуральных значений факторов в кодированным.
Точка начала эксперимента называется базовой (нулевой) точкой. Это центр плана эксперимента. Базовую точку 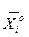 выбирают возможно ближе к центру области факторного пространства, в которой ведется математическое описание объекта. Такой точкой является оптимальная комбинация уровней факторов, установленная в результате анализа априорной информации.
выбирают возможно ближе к центру области факторного пространства, в которой ведется математическое описание объекта. Такой точкой является оптимальная комбинация уровней факторов, установленная в результате анализа априорной информации.
Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня. Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний уровень фактора, а вычитание - нижний. Таким образом, выбрав интервал варьирования, определяют крайние уровни факторов. При планировании масштабы данных по осям принимаются такими, чтобы верхний уровень соответствовал +1, нижний - -1, основной - 0.
Если область определения фактора непрерывна, выбор масштаба производится согласно формуле
хi = 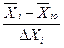 ( 13 )
( 13 )
где xi- кодированное значение фактора;
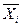 - натуральные значения основного фактора;
- натуральные значения основного фактора;
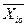 -натуральное значение нулевого уровня;
-натуральное значение нулевого уровня;
 ΔХi - интервал варьирования;
ΔХi - интервал варьирования;
i - номер фактора.
B табл.2 приведен пример кодированных значений для одного фактора, рассчитанных по формуле (13).
Интервал варьирования не может быть меньше погрешности измерения факторa, иначе верхний и нижний уровни окажутся неразличимыми. С другой стороны, интервал не может быть больше пределов области определения, чтобы верхний или нижний уровни оказались за пределами области определения факторов. Поэтому интервал варьирования выбирают равным 0,05...0,3 от допустимого диапазона изменений факторов, т.е. область варьирования составляет 10...60% от всего диапазона.
Для упрощения обработки результатов эксперимента и интерпретации результатов переходят от натуральных значений факторов 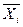 , к кодированнымбезразмерным значениям
, к кодированнымбезразмерным значениям
2. Кодированные значения фактора
| Натуральное значение фактора, º С | 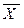
| |||
| Кодированное значение фактора | х | -1 | +1 |
На рис. показан в факторном пространстве симметричный двухуровневый план для двухфакторной функции отклика y=f(x1x2) в натуральном (рис.4,а) и кодированном (рис.4,б) представлении уровней факторов. Здесь 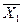 ,
, 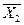 - искомые натуральные уровни факторов,
- искомые натуральные уровни факторов, 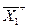 ,
, 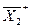 , +1,+1 – верхние уровни факторов
, +1,+1 – верхние уровни факторов 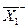 ,
, 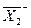 , -1,-1 – нижние уровни,
, -1,-1 – нижние уровни, 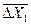 ,
, 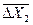 - интервалы варьирования.
- интервалы варьирования.
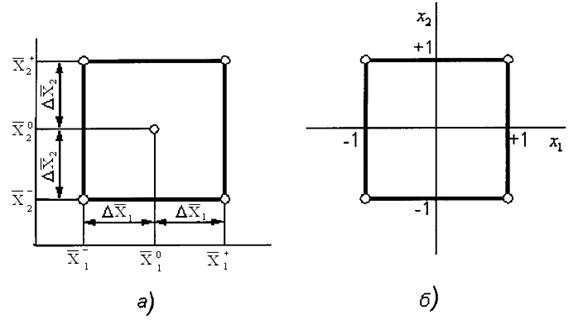
Рис. 4 Симметричный двухуровневый план для двухфакторной функции отклика
При выборе интервала варьирования используют априорную информацию, содержащую сведения о точности измерения факторов, кривизне поверхности отклика и о диапазоне изменения выходной величины. Однако в виду того, что такая информация может оказаться не всегда достоверной, в ходе эксперимента ее нередко приходится корректировать.
Все возможные сочетания уровней изучаемых факторов встречаются при полном факторном эксперименте (ПФЭ). В этом случае количество испытаний N равно взаимному произведению чисел уровней каждого из факторов. Если число уровней n каждого из факторов одинаково, то N=an, где a - количество факторов. Для десяти факторов, имеющих по четыре уровня, k=410 =104876. В подобных случаях схему ПФЭ практически реализовать невозможно.
Активные эксперименты ставятся таким образом, что в каждом опыте независимые факторы варьируются по специальному плану. Методы активного планирования эксперимента позволяют нейтрализовать пропущенные сочетания уровней.
Матрица планирования полного факторного эксперимента ( ПФЭ)
Полный факторный эксперимент (ПФЭ) характеризуется тем, что число уровней каждого фактора равно двум. При соблюдении этого условия число N опытов, необходимых для реализации всех возможных сочетаний уровней факторов составляет 2n, где n - число факторов.
Согласно этому плану для двухфакторного эксперимента должно быть проведено четыре опыта. Условия проведения эксперимента записываются в виде таблицы, называемой матрицей планирования (матрица Адамара). Каждый столбик матрицы называют вектор-столбцом, а каждую строку – вектор-строкой (табл.3).
В общем случае максимальное количество факторов, которое может быть исследовано с помощью матрицы ПФЭ 2n для линейной модели равно 2n -1. План с предельным числом факторов для данной матрицы планирования 2n называется насыщенным. Таким образом, для трех факторов план 2² с четырьмя опытами является насыщенным (2²-1=3).
Для матрицы ПФЭ 23 максимальное количество факторов, которое может быть исследовано, равно семи (2³-1=7). В этом случае четыре фактора приравниваются к эффектам взаимодействия: x4 = x1x2 , x5 = x1x3 , x6 = x2x3 , x7 = x1x2x3 .
Правила построения матрицы планирования эксперимента.
1. В первой строке все факторы устанавливаются на нижнем уровне
х i = -1,
2. Последующие строки формируются по следующему правилу: при последовательном переборе точек факторного пространства (строк матрицы планирования) частота смены знака для каждого последующего фактора х i+1 вдвое меньше, чем для предыдущего xi .
3. Все взаимодействия факторов xi·xj для каждой точки факторного пространства получаются перемножением нормированных значений соответствующих факторов.
Проведение ПФЭ позволяет оценить не только силу влияния факторов на отклик, но и эффекты взаимодействия: например, как добавление одних микроингредиентов будет стимулировать влияние других на качество выпускаемого продукта.
Столбцы матрицы, соответствующие факторам х 1 , х 2 , ..., хn (в табл. 5 и 6 обведены) образуют матрицу спектра плана. Вся матрица, включающая фиктивный столбец и взаимодействия факторов, часто называется расширенной информационной матрицей.
3. Матрица планирования ПФЭ 22
| Номер опыта | х1 | х2 | y |
| -1 | -1 | y1 | |
| +1 | -1 | y2 | |
| -1 | +1 | y3 | |
| +1 | +1 | y4 |
При построении матрицы ПФЭ 22 комбинации уровней находятся прямым перебором. Если количество факторов более двух, используют три приема перехода от матрицы меньшей размерности к матрицам большей размерности.
При выполнении первых двух приемов сначала строится матрица ПФЭ 22, а затем – матрица ПФЭ 23 (табл.4) и большей размерности.
4. Матрица планирования ПФЭ 23
| Номер опыта | х1 | х2 | х3 | у |
| -1 | -1 | -1 | у1 | |
| +1 | -1 | -1 | у2 | |
| -1 | +1 | -1 | у3 | |
| +1 | +1 | -1 | у4 | |
| -1 | -1 | +1 | у5 | |
| +1 | -1 | +1 | у6 | |
| -1 | +1 | +1 | у7 | |
| +1 | +1 | +1 | у8 |
Первый прием основан на том, что при добавлении нового фактора каждая комбинация уровней, имеющихся в матрице меньшей размерности, в матрице большей размерности встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Поэтому сначала описывается исходный план для одного уровня фактора, а затем он повторяется для другого уровня (см. табл. 3).
Второй прием основан на построчном перемножении двух столбцов согласно правилу знаков: одноименные знаки перед единицей при перемножении дают +1, разноименные - -1. После перемножения получается вектор-столбец произведений х1х2 в исходном плане. Затем исходный план продлевается по числу опытов вдвое путем повторения предыдущего исходного плана (включая столбец х1х2). Далее удлиненный вдвое исходный план вновь повторяется, но вместо столбца произведений записывается столбец добавленного фактора х3 с изменением на противоположные знаки столбца х1х2. Этот прием несколько сложней, чем первый.
Третий прием основан на правиле чередования знаков. В матрице, включающей 2n опытов, знаки первого столбца меняются поочередно, знаки второго столбца - через два, третьего - через четыре, четвертого - через восемь и т.д. по степеням двойки.
Матрица планирования эксперимента обладает четырьмя общими свойствами. Два свойства относятся к особенностям построения вектор-столбцов и следуют непосредственно из правил построения матрицы.
Свойства матрицы планирования эксперимента
Первое свойство - симметричность относительно центра эксперимента – проявляется в правиле: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю, т.е.  xij =0,
xij =0,
где i - номер опыта,
j - номер фактора,
N - число опытов.
Второе свойство (условие нормировки): сумма квадратов каждого столбца равна числу опытов, т.е.  xij2 =N.
xij2 =N.
Два других свойства относятся к совокупности столбцов матрицы.
Третье свойство - ортогональность матрицы, когда сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю, т.е.
 xij xin=0 , j¹n.
xij xin=0 , j¹n.
Это правило используется при построении плана эксперимента, то есть при определении каким образом нужно менять значения факторов в опытах. Это правило показывает, что в ортогональном планировании при четном числе уровней, на которых фиксируется каждый фактор, то эти уровни должны быть симметрично расположены относительно центральной точки х=0, при нечетном числе уровней должна использоваться и центральная точка
ПФЭ обладает ортогональной матрицей планирования. Ортогональность позволяет оценивать коэффициенты модели регрессии независимо друг от друга, т.е. избавиться от неопределенности, связанной с неоднозначным оцениванием этих коэффициентов.
Четвертое свойство (ротатабельность): точки в матрице планирования подбираются так, что точность предсказаний значений выходного параметра на основании математической модели одинакова на равных расстояниях от центра эксперимента и не зависит от направления, т.е. дисперсия отклика одинакова на одном расстоянии от центра плана при любом направлении в факторном пространстве. В упрощенном виде это означает, что все точки плана лежат на окружности (сфере, гиперсфере).
Если матрица обладает всеми четырьмя свойствами, то она составлена правильно.
Определение коэффициентов линейной регрессионной модели при планировании эксперимента
|
y = b0 + b1 x1 + b2 x2.
После проведения опытов неизвестными величинами в этом выражении будут только коэффициенты b0, b1, b2. Для N опытов можно составить систему линейных условных уравнений. После ее решения методом наименьших квадратов определяются оценки коэффициентов:
bj= 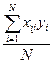 ( 15)
( 15)
Так, при N=4 получим:
b1 = [(-1)y1 + (+1)y2 +(-1)y3 +(+1)y4] / 4;
b2 = [(-1)y1 + (-1)y2 +(+1)y3 +(+1)y4] / 4.
Таким образом, благодаря кодированию факторов расчет коэффициентов превратился в простую процедуру.
Запишем уравнение y = b0 х0 + b1 x1 + b2 x2 для средних арифметических значений переменных.
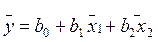 (16 )
(16 )
Так как матрица обладает свойством симметрии, то 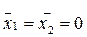 , поэтому
, поэтому 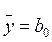 .
.
Для того чтобы получить возможность определения b 0 по формуле (15), в матрицу вводят фиктивную переменную х0, которая во всех опытах принимает значение +1. Составленная линейная модель несколько видоизменяется:
у= b0 х0 + b1 x1 + b2 x2.
Положительные коэффициенты при хij пропорциональны степени влияния факторов, отрицательные - обратно пропорциональны.
Линейная модель не всегда в полной мере описывает объект исследования. Часто нелинейность связана с взаимным влиянием факторов, и задачей полного факторного эксперимента является установление степени такого взаимодействия. Для этого перемножением столбцов матрицы получают новый столбец произведений двух факторов так, что матрица размерности 22 будет иметь вид, представленный в табл.4.
5. Матрица планирования эксперимента 22 с учетом взаимодействия факторов
| Номер опыта | х0 | х1 | х2 | х1х2 | у |
| +1 | -1 | -1 | +1 | у1 | |
| +1 | +1 | -1 | -1 | у2 | |
| +1 | -1 | +1 | -1 | у3 | |
| +1 | +1 | +1 | +1 | у4 |
С учетом взаимодействия факторов х1х2 видоизменяется модель
у= b0 х0 + b1 x1 + b2 x2 + b12х1х2. (16)
Коэффициент b12 вычисляется также по формуле (15) :
b12 = [(+1)y1 + (-1)y2 +(-1)y3 +(+1)y4] / 4.
Чем больше факторов, тем больше число возможных взаимодействий. Так, в матрице планирования 23 появляются новые вектор-столбцы х1х2, х1х3, х2х3 , характеризующие эффект взаимодействия первого порядка, и столбец х1х2,х3 , - эффект взаимодействия второго порядка. В общем случае эффект взаимодействия максимального порядка имеет порядок на единицу меньше числа факторов. Применяются также такие понятия, как парные эффекты взаимодействия (х1х2, х1х3, х2х3), тройные (х1х2х3, х3х4х5) и т.д.
Суммарное количество коэффициентов (в том числе b0, линейные эффекты и эффекты взаимодействия) равно числу опытов, проводимых согласно матрице эксперимента. Значения различных коэффициентов независимы друг от друга.
|
у= b0 + b1 x1 + b2 x2 + b3 x3+ b12 х1х2 + b13 х1х3 + b23 х2 х3+ b123 х1 х2 х3.
то матрица планирования ПФЭ выглядит следующим образом:
6. Матрица планирования эксперимента 23 с учетом взаимодействия факторов
| № опыта | x0 | x1 | x2 | x3 | х1х2 | х1х3 | х2х3 | х1 х2 х3 | у |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | у1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | у2 | |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | у3 | |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | у4 | |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | у5 | |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | у6 | |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | у7 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | у8 |
Если модель включает не только линейные эффекты и эффекты взаимодействия, но и квадраты, кубы и т.д. факторов, то подход к оценке коэффициентов несколько иной.
Если, например, при двухфакторном эксперименте заметное влияние имеет квадратичный член, то модель можно записать следующим образом:
у= b0 х0 + b1 x1 + b2 x2 + b12х1х2 + b11х21 + b22х22 . (18)
Если мы захотим построить матрицу планирования эксперимента с добавлением вектор-столбцов х21 и х22 (табл. 7), то получим единичные столбцы, совпадающие друг с другом и со столбцом х0, в результате чего невозможно определить, за счет чего получилось значение b0. Полученную для такого случая оценку b0 называют смешанной, так как она определяется совместными вкладами свободного и квадратичных членов.
7. Матрица планирования эксперимента 22 с учетом квадратичности факторов
| № опыта | x0 | x1 | x2 | x3= х1х2 | х4=х12 | х5=х22 | у |
| +1 | -1 | -1 | +1 | +1 | у1 | ||
| +1 | +1 | -1 | -1 | +1 | +1 | у2 | |
| +1 | -1 | +1 | -1 | +1 | +1 | у3 | |
| +1 | +1 | +1 | +1 | +1 | у4 |
Итак, полный факторный эксперимент при варьировании факторов на двух уровнях позволяет оценить линейные эффекты эксперимента.
Из-за действия неучтенных (неконтролируемых или неуправляемых) факторов отклик объекта носит случайный характер. Поэтому для каждого сочетания факторов, т.е. в каждой точке факторного пространства, обычно выполняется не один, а серия из m опытов, которые называются параллельными (дублированными). Дублирование позволяет проверить воспроизводимость эксперимента и адекватность модели и исследуемого процесса. В качестве значений отклика принимается среднее арифметическое ỳ i из m измерений. Матрица планирования эксперимента с параллельными опытами представлена в таблице 8.
8. Матрица планирования эксперимента с параллельными опытами
| № | x1 | x2 | ... | xK | Параллельные опыты | 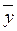 i i
| |||
| опыта | ... | m | |||||||
| -1 | -1 | ... | -1 | у11 | у12 | ... | у1m | 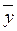 1 1
| |
| +1 | -1 | ... | +1 | у21 | у22 | ... | у2m | 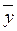 2 2
| |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| n | +1 | +1 | ... | +1 | уn1 | уn2 | ... | уnm | 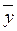 n n
|
Планирование дробного факторного эксперимента
Дробный факторный эксперимент, сохраняя все свойства полного факторного эксперимента (симметричность, выполнение условия нормировки, ортогональность, рототабельность), проводится при меньшем числе опытов. Возможность сокращения числа опытов при использовании линейной модели предоставляется в связи с тем, что в полном факторном эксперименте число опытов больше числа коэффициентов модели.
Для пояснения принципа, на котором основано сокращение числа опытов, обратимся к матрице 22 полного факторного эксперимента, представленной в табл. 5. Используя эту матрицу, можно вычислить четыре коэффициента модели. Однако при принятом условии линейности модели b12=0 достаточно определить три коэффициента: b0, b1, b3, вектор-столбец х1х2 можно использовать для нового фактора х3.
Если проверить возможность смешивания оценок, то можно заметить, что оно имеет место при различных сочетаниях вектор-столбцов в связи с их совпадением. Однако благодаря тому, что модель линейна, парные взаимодействия незначительны, и взаимодействия практически не влияют на достоверность вычисленных оценок.
Таким образом, оказалось, что для изучения трех факторов достаточно поставить четыре опыта вместо восьми. Сказанное можно обобщить правилом: для сокращения числа опытов новому фактору следует присвоить без изменения знаков вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь.
Матрица 22 (табл.5) с заменой х1х2 на х3, представляющая собой половину матрицы 23 полного факторного эксперимента, называется полурепликой.
9. Матрица планирования дробного факторного эксперимента 23
| Номер опыта | х0 | х1 | х2 | х3 | х1х2 | х1х3 | х2х3 | х1х2 x3 | у |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | у1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | у2 | |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | у3 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | у4 |

Вторую половину матрицы 23 с постановкой четырех опытов для оценки влияния трех факторов можно получить, если в матрице 22 х3 приравнять с обратным знаком к х1х2 . При объединении двух полуреплик получим полный факторный эксперимент. Каждая из полуреплик может быть использована как для получения оценки линейных эффектов, так и эффектов взаимодействия таким же образом, как и в полном факторном эксперименте 23. Кроме полуреплик находят применения другие виды дробных реплик (1/4, 1/8, 1/16), каждая из которых имеет две разновидности, которые отличаются числом с линейных эффектов, приравненных к эффектам взаимодействия, и условным обозначением в виде 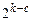 (табл.10).
(табл.10).
10. Число опытов при планировании дробных экспериментов.
| Число факторов | Дробная реплика | Условное обознач. | Число опытов | |||
| для дробных реплик | для полного факторного эксперим. | |||||
| 1/2 - реплика от 23 | 23-1 | |||||
| 1/2 - реплика от 24 | 24-1 | |||||
| 1/4 - реплика от 23 | 25-2 | |||||
Таким образом, применение дробного факторного эксперимента позволяет существенно сократить число опытов, необходимых для построения модели (16 вместо 256 при восьмифакторном эксперименте). Наиболее целесообразно использовать дробные реплики для получения линейных моделей с большим количеством факторов.
Проведение обработки результатов эксперимента
Проведение эксперимента, связанного с измерением величин, сопровождается погрешностями измерений, вносящими элемент
неопределенности в результат эксперимента. Постановка повторных или параллельных опытов полностью не исключает неопределенность, так как они проводятся также с погрешностью воспроизводимости.
| <== предыдущая страница | | | следующая страница ==> |
| Правила построения моделей | | | Проверка воспроизводимости эксперимента |
Дата добавления: 2014-10-17; просмотров: 1557; Нарушение авторских прав

Мы поможем в написании ваших работ!