
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Проверка воспроизводимости эксперимента
Если проводятся параллельно несколько опытов в одинаковых условиях, то погрешность воспроизводимости можно оценить по отклонениям результатов опыта от среднего арифметического, характеризуемого оценкой дисперсии. Дисперсией называют среднее арифметическое квадрата отклонений величины от среднего значения. Дисперсия обозначается S2 и определятся формулой
|
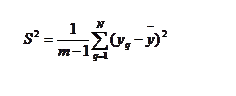
где m – число параллельных опытов, при условии исключения грубых погрешностей; m-1 – число степеней свободы.
Для получения оценки дисперсии эксперимента нужно усреднить оценки дисперсии всех опытов, предусмотренных матрицей планирования. Оценку дисперсии воспроизводимости эксперимента подсчитывают по формуле
|
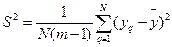
Если из-за отбрасывания промахов число m повторных опытов во всех точках неодинаково, оценка дисперсии эксперимента определяется по формуле
|
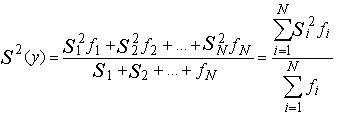 ,
,
где Si– оценка дисперсии i-го опыта; fi – число степеней свободы в i-м опыте; равное числу параллельных опытов ni минус один.
Число степеней свободы средней дисперсии принимается равным сумме чисел степеней свободы fi. Формулы расчета дисперсии эксперимента справедливы только тогда, когда дисперсии однородны, т.е. если среди суммируемых дисперсий не было бы таких, которые превышали бы все остальные.
Оценка воспроизводимости эксперимента основывается на проверке гипотезы об однородности выборочных дисперсий Si2 отклика. Осуществляется с помощью попарных сравнений по критерию Фишера (F-критерий) или с помощью критерия Кохрена
G = 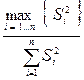 ( 22 )
( 22 )
с m-1 и n степенями свободы.
Если при заданном уровне значимости α (0,95) наблюдаемое значение G меньше найденного из таблиц критического значения Gкр , то нет оснований отвергать гипотезу об однородности дисперсий Si2 и можно считать, что эксперимент воспроизводим. В противном случае следует попытаться увеличить число параллельных опытов или отбросить резко выделяющиеся значения отклика.
Если дисперсии Si2 однородны, то вычисляется оценка дисперсии воспроизводимости по формуле
S 2вос = 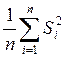 (23 )
(23 )
с n (m-1) степенями свободы.
Дисперсия воспроизводимости является дисперсией отклика и позволяет оценивать влияние на отклик неучтенных, шумовых факторов.
Наряду с оценкой случайных погрешностей измерений должны быть приняты меры по уменьшению влияния систематических погрешностей, вызванных изменением внешних условий. Для этих целей оказывается эффективной «рандомизация» (от random – случайный) опытов во времени приданием случайного характера последовательности проведения опытов, предусмотренных матрицей планирования. Она позволяет предупредить влияние изменения температуры и влажности воздуха и сырья, изменения состава и характеристик сырья, износ рабочих органов. К примеру, в матрице спектра ПФЭ в первой половине опытов фактор Xi находится на нижнем уровне, а в последних - на верхнем. Если первая половина опытов ставится в один день, а другая - через неделю, то изменение внешних условий может вызвать появление систематических ошибок в определении отклика. При рандомизации последовательность проведения опытов ПФЭ выбирается случайно или последовательно отдельными блоками.
Обработка результатов эксперимента сводится к последовательному выполнению трех операций:
- вычислению коэффициентов модели (коэффициентов регрессии);
- проверке значимости отдельных коэффициентов регрессии;
- проверке адекватности модели.
Вычисление коэффициентов модели производится с привлечением метода наименьших квадратов.
Получение оценок коэффициентов модели
|
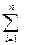 ( yi –f (xi))2 . Для линейной модели с n факторами при ПФЭ коэффициенты независимы и вычисляются по формуле bj=
( yi –f (xi))2 . Для линейной модели с n факторами при ПФЭ коэффициенты независимы и вычисляются по формуле bj= 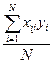
|
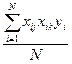
| <== предыдущая страница | | | следующая страница ==> |
| Однофакторный эксперимент | | | Проверка значимости коэффициентов математической модели |
Дата добавления: 2014-10-17; просмотров: 1231; Нарушение авторских прав

Мы поможем в написании ваших работ!