
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Понятия об иерархиях
Математическая модель иерархии
Существует несколько видов иерархий:
- доминантные иерархии, среди которых выделяются полные и неполные;
- холархии, когда есть обратная связь.
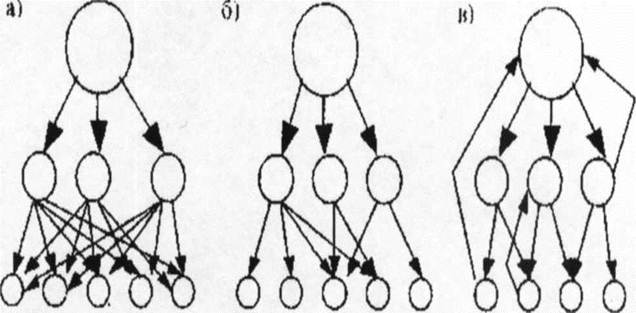
а) полная; б) неполная; в) холархия.
Построение иерархий (структуризация отношений)
Иерархия может формализованной в виде бинарной матрицы. Бинарная матрица может быть представлена матрицей достижимости, которая определяется матрицей зависимости. Рассмотрим на следующем примере:
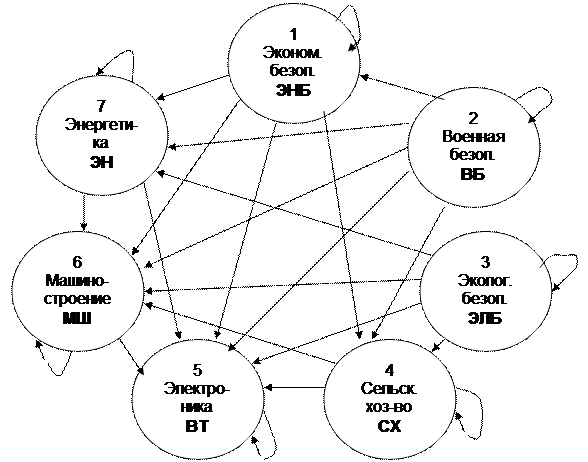
1. Экономическая безопасность.
2. Военная безопасность.
3. Экологическая безопасность.
4. Сельское хозяйство.
5. Электроника.
6. Машиностроение.
7. Энергетика.
Матрица зависимости В заполняется следующим образом. Если множество вершин определено, то с помощью бинарного отношения «зависит от» можно заполнить матрицу так, что ответ «да» фиксируют «единицей», а ответ «нет» фиксируют «нулём», т. е. элементы матрицы равны:
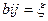
1 если i зависит от j;
0 если i не зависит от j.
Матрица зависимости для нашего графа:
| ЭНБ | ВБ | ЭЛБ | СХ | ВТ | МШ | ЭН | |
| ЕНБ | |||||||
| ВБ | |||||||
| ЭЛБ | |||||||
| СХ | |||||||
| ВТ | |||||||
| МШ | |||||||
| ЭН |
i – достижимые;
j – предшествующие.
Сформируем матрицу достижимости. Она строится также по исходному графу заполняется таблица бинарными элементами. Осуществляется по строке слева - направо за правилом 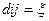 .
.
1, если с i элемента можно попасть в j;
0, если нет.
| ЭНБ | ВБ | ЭЛБ | СХ | ВТ | МШ | ЭН | |
| ЕНБ | |||||||
| ВБ | |||||||
| ЭЛБ | |||||||
| СХ | |||||||
| ВТ | |||||||
| МШ | |||||||
| ЭН |
Наличие матрицы достижимости позволяет разделить все множество вершин на множество уровней, для этого все вершины делятся на достижимые и предшествующие. Вершина hi называется достижимой из вершин hj, если в ориентированном графе существует путь из hj к hi.
Вершину hj называют предшествующей вершине hi, если возможно достижение hi из hj.
R (hi) – достижимые,
A (hj) – предшествующие.
Множество тех вершин, для которых выполняется условие недостижимости из любой из оставшихся вершин множества и, следовательно, может быть обозначено как уровень иерархии. Необходимо выполнить следующие процедуры:
1. Составить направленный граф отношений между элементами множества.
2. Сформировать матрицу достижимости по направленному графу.
3. Сформировать таблицу с элементами hi, R(hj), A(hi), R(hj)∩A(hi).
Для формирования подмножества R(hj) из j-й строки матрицы достижения выписываются номера тех элементов, которые содержат единицы. Для формирования подмножества A(hi) из i-го столбца матрицы достижимости выписываются номера тех элементов, которые содержат единицы.
Подмножество R(hj)∩A(hi) формируется как логическое пересечение элементов двух подмножеств R и А.
4. Найти элементы в таблице, для которых выполняется условие логического пересечения: эти элементы и образуют первый уровень.
5. Вычеркнуть полученные на первой итерации элементы и применить вышеописанные процедуры (п.1-4) снова. Итерации повторяются до тех пор, пока остаётся более одного элемента.
| Hi | R(hj) | A(hi) | R(hj)∩A(hi) |
| 1,4,5,6,7 | 1,2 | ||
| 1,2,4,5,6,7 | |||
| 3,4,5,6,7 | |||
| 4,5,6 | 1,2,3,4 | ||
| 1,2,3,4,5,6,7 | |||
| 5,6 | 1,2,3,4,6,7 | ||
| 5,6,7 | 1,2,3,7 |
Критерием равенства A(hi)= R(hj)∩A(hi) является формула пересечений R(hj)∩A(hi) на первой итерации она выполняется для элементов 2 и 3, следовательно, они являются элементами 1-го уровня. Вычеркивая из таблицы строки с номерами 2 и 3 и убирая из всех последовательностей цифры 2 и 3, получаем 2-ю итерацию, для которой критериальное равенство выполняется для элемента 1, следовательно, на 2-м уровне будет 1 элемент.
| <== предыдущая страница | | | следующая страница ==> |
| Агрегирование | | | Рекомендации к построению иерархий |
Дата добавления: 2014-11-06; просмотров: 298; Нарушение авторских прав

Мы поможем в написании ваших работ!