Композиция подстановок

Основной операцией на множестве подстановок является композиция.

Пусть имеются две подстановки q={u1/s1,… ,um/sm} и y={v1/t1,,…, vn/tn}.

Композицией q и y называется подстановка qy={u1/s1y,…, um/smy, v1/t1, …, vn/tn} \ ({ui/siy | ui=siy} È {vi/ti | viÎ{u1,…, um}}).

При выполнении композиции подстановок сначала применяется подстановка y в термы s1,…, sm подстановки q, а затем полученная подстановка дополняется элементами множества y. При этом отбрасываются элементы вида ui/siy, если терм siy совпадает с ui, и элементы вида vi/ti, если viÎ{u1,…, un}.

Пример. Рассмотрим две подстановки: q={x/f(y), y/z} (в качестве {ui /si}) и y={x/a, y/b, z/y} (в качестве {vi / ti}).

Согласно определению композиция подстановок q и y имеет вид:

q y ={x/f(y)y, y/zy,x/a, y/b, z/y} \ ({ui/si | ui=siy}È{vi/ti | viÎ{uj}})=

= {x/f(b), y/y, x/a,y/b, z/y} \ ({y/y}È{x/a, y/b}) = {x/f(b), z/y}.

Пример. Рассмотрим терм w(f(v1), h(x), f(v2), v3) и подстановки

q={v1/f(g(x)), v2/h(v1), v3/h(v3)}, y={x/z, v1/v2, v3/v1}.

Определим композицию подстановок:

qy={v1/f(g(x)) y, v2/h(v1) y, v3/h(v3) yx/z, v1/v2, v3/v1} \ (Æ È {v1/v2, v3/v1}) =

={v1/f(g(z)), v2/h(v2), v3/h(v1), x/z}.

Следовательно,

w(qy)=w(f(f(g(z))), h(z), f(h(v2)), h(v1)).

Отметим также, что

(wq)y= w(f(f(g(x))), h(x), f(h(v1)), h(v3))y

=w(f(f(g(z))), h(z), f(h(v2)), h(v1))=t(qy).

Из второго примера можно заключить, что операция композиции подстановок ассоциативна.

Для произвольных подстановок q, y, g и для произвольного терма t выполняются равенства:

qЕ =Еq = q;

(tq) y = t(qy);

(qy)g = q(yg).

Если S={C1,…, Ck} – множество бескванторных формул логики предикатов, то множество Sq= {C1q,…, Ckq} есть результат замены формул СiÎS на формулы Ciq,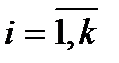

Два множества формул без кванторов называются вариантами, если можно подобрать такие две подстановки q и y, что S1=S2q, а S2 = S1y.

Пример. Множества дизъюнктов S1={P(f(x,y)), Q(h(z),b)} и S2={P(f(y,x)), Q(h(u), b)}, где b – константа, являются вариантами. Действительно, если q={x/y, y/x, z/u} и y= {x/y, y/x, u/z}, то

S1q= {P(f(x,y)) q, Q(h(z), b) q} = {P(f(y,x)), Q(h(u),b)} = S2,

S2Ψ= {P(f(y,x)) Ψ, Q(h(u), b) Ψ } = {P(f(x,y)), Q(h(z), b)} = S1.

Переименованием называется подстановка вида

{v1/u1,…, vn/un},

где переменные.

Дата добавления: 2014-11-08; просмотров: 393; Нарушение авторских прав

Мы поможем в написании ваших работ!