Корректность и полнота метода семантических таблиц

Теорема о полноте исчисления Бета. Если предложение s является следствием множества предложений S, то оно выводимо по Бету из S.

S ╞ s, то S ├B s

Следствие. Если предложение s общезначимо, то оно выводимо по Бету.

Теорема корректности исчисления Бета. Если предложение s выводимо по Бету из множества предложений S логики предикатов, то s является следствием S:

S ├B s, то S ╞ s

Следствие: если предложение выводимо по Бету, то оно общезначимо:

├B s, то ╞ s

Теорема компактности. Множество предложений S выполнимо тогда и только тогда, когда каждое подмножество S выполнимо.

Корректность и полнота исчисления резолюций

Теорема корректности исчисления резолюций. Пусть S – множество дизъюнктов, и R*(S) – множество резольвент S. Если множество R*(S) содержит пустой дизъюнкт, то S не выполнимо: ÎR*(S) Þ S не выполнимо.

Теорема полноты исчисления резолюций. Пусть S – множество дизъюнктов, и R*(S) – множество резольвент S. Если S не выполнимо, то множество R*(S) содержит пустой дизъюнкт:

S не выполнимо Þ ÎR*(S)

Содержательно эта теорема означает, что для доказательства выполнимости или не выполнимости предложения методом резолюций, достаточно вывести пустой дизъюнкт из соответствующего множества дизъюнктов. Если имеется непротиворечивое множество дизъюнктов S, из которого следует вывести заключение j, то мы применяем метод резолюции к множеству дизъюнктов SÈS`, где S`={ 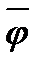}. Если результатом добавления к множеству предложений S предложения 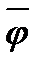станет получение пустого дизъюнкта в резолютивном выводе, это докажет, что общезначимо j.

Дата добавления: 2014-11-08; просмотров: 346; Нарушение авторских прав

Мы поможем в написании ваших работ!