
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Элементы теории отношений
Отношения устанавливают связь между объектами по какому-то правилу или закону.
Отношения бинарное, если связь устанавливается между парами объектов, т.е. оно полностью определяется множеством пар, связанных этим отношением. Обозначается  .
.
Например, 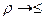 ; X = {1,2,3} – множество объектов
; X = {1,2,3} – множество объектов
 = {<1,2>,<1,3>,<2,3>,<1,1>,<2,2>,<3,3>}
= {<1,2>,<1,3>,<2,3>,<1,1>,<2,2>,<3,3>}
Любое бинарное отношение – подмножество декартова произведения некоторых двух множеств. Первый элемент каждой пары бинарного отношения называется первой координатой, второй элемент - второй координатой.
Множество всех первых координат отношения – область определения. Обозначается D0. В нашем примере 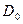 = { 1,2,3}
= { 1,2,3}
Множество всех вторых координат отношения – область значения. Обозначается Dз. Dз = {1,2,3}
Сечением отношения по элементу х называется множество всех тех вторых координат, для которых первой координатой является х.
 (1) = {1,2,3};
(1) = {1,2,3};
 (2) = {2,3};
(2) = {2,3};
 (3) = {3}.
(3) = {3}.
Способы задания отношений:
1. Аналитические (3 штуки).
2. Матричный.
3. Графический.
1. Аналитические:
• перечислением:
 = {<1,1>,<1,2>,<2,3>};
= {<1,1>,<1,2>,<2,3>};
• с помощью определяющего свойства: X,  = {<xi,xj> | P(xi,xj)};
= {<xi,xj> | P(xi,xj)};
• с помощью фактор-множества: это матрица 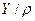 , где первая строка - все первые координаты отношения, а вторая - сечение отношения по этим координатам.
, где первая строка - все первые координаты отношения, а вторая - сечение отношения по этим координатам.

 Пример:
Пример:  = {<1,1>,<1,2>,<2,3>}
= {<1,1>,<1,2>,<2,3>}
1 2
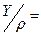 {1,2} {3} - фактор – множество
{1,2} {3} - фактор – множество
2. Матричный способ.
Строки матрицы – первые координаты, столбцы – вторые координаты. На пересечении строки i и столбца j ставится 1, если пара <xi,xj>Î 
 = {<1,2>,<1,3>,<2,3>}
= {<1,2>,<1,3>,<2,3>}



 2 3
2 3
 1 1 1
1 1 1
 2 1
2 1
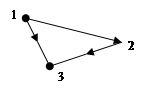
3. Графический способ.
Первые и вторые координаты - точки на плоскости. Строится ориентированная связь i 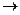 j, если пара <xi,xj>Î
j, если пара <xi,xj>Î 
 |
Операции над отношениями:
Так как все отношения есть множества, то все операции над множествами справедливы и для отношений.
 1È
1È  2;
2;  1∩
1∩  2;
2;  1\
1\  2;
2;  1÷
1÷  2;
2; 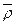 где
где 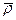 = (Do
= (Do 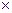 Dз)\
Dз)\ 
Дополнительно определены две специальные операции:
1) обращения (симметризации): 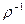 - меняем местами первые и вторые координаты;
- меняем местами первые и вторые координаты;
2) композиции:  3=
3=  1∙
1∙  2
2
Пусть X,Y,Z – три множества.
 1
1 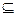 X
X 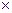 Y
Y
 2
2 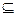 Y
Y 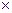 Z
Z
Отношение  3=
3=  1∙
1∙  2 называется композицией
2 называется композицией  1 и
1 и  2 и состоит из пар <x,z>, для которых <x,y>
2 и состоит из пар <x,z>, для которых <x,y> 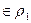 , <y,z>
, <y,z> 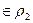 .
.
Пример:  1 = {<x1,y1>,<x1,y2>,<x2,y2>,<x3,y2>}
1 = {<x1,y1>,<x1,y2>,<x2,y2>,<x3,y2>}
 2 = {<y1,z1>,<y1,z2>,<y2,z1>}
2 = {<y1,z1>,<y1,z2>,<y2,z1>}
 3 = {<x1,z1>,<x2,z1>,<x3,z1>,<x1,z2>}
3 = {<x1,z1>,<x2,z1>,<x3,z1>,<x1,z2>}
Свойства отношений:
1. Рефлексивность;
2. Симметричность;
3. Транзитивность.
Рефлексивность:
Отношение на множестве X называется рефлексивным, если " xi Î X справедливо < xi, xi > Î  .
.
Пример: X = {1, 2, 3}
 = {<1,1>,<2,2>,<3,3>,<1,2>,<1,3>} – рефлексивно.
= {<1,1>,<2,2>,<3,3>,<1,2>,<1,3>} – рефлексивно.
Отношение антирефлексивно на множестве X, если " xi Î X справедливо
<xi, xi> Ï  .
.
Пример: X = {1, 2, 3}
 = {<1,2>,<1,3>,<2,1>}
= {<1,2>,<1,3>,<2,1>}
Отношение на множестве X называется нерефлексивным, если для некоторых элементов xi Î X рефлексивность выполняется, а для некоторых – нет.
Пример:  = {<1,1>,<2,3>,<1,2>}
= {<1,1>,<2,3>,<1,2>}
Симметричность:
Отношение называется симметричным, если " <xi, xj> Î  пара <xj, xi> Î
пара <xj, xi> Î  тоже.
тоже.
Пример:  = {<1,1>,<2,2>,<3,3>,<1,2>,<2,1>}
= {<1,1>,<2,2>,<3,3>,<1,2>,<2,1>}
Отношение антисимметрично, если " <xi, xj> Î  пара <xj, xi> Ï
пара <xj, xi> Ï  .
.
Пример:  = {<1,1>,<1,2>,<2,3>} – несмотря на <1,1>!
= {<1,1>,<1,2>,<2,3>} – несмотря на <1,1>!
Отношение несимметрично, если для некоторых пар симметричность выполняется, а для некоторых – нет.
Транзитивность:
Отношение транзитивно, если для всякой пары <xi, xj> Î  и пары <xj, xz> Î
и пары <xj, xz> Î  пара <xi, xz> Î
пара <xi, xz> Î  тоже, либо для пары <xi, xj> отношения пары <xj, ?> нет вообще.
тоже, либо для пары <xi, xj> отношения пары <xj, ?> нет вообще.
Пример:  = {<1,2>,<2,3>,<1,3>} – транзитивно.
= {<1,2>,<2,3>,<1,3>} – транзитивно.
Специальные типы бинарных отношений:
1. Отношение эквивалентности (рефлексивно, симметрично, транзитивно);
2. Отношение порядка (рефлексивно, антисимметрично, транзитивно);
 (≤) X = {1,2,3}
(≤) X = {1,2,3}
 = {<1,1>,<2,2>,<3,3>,<1,2>,<1,3>,<2,3>}
= {<1,1>,<2,2>,<3,3>,<1,2>,<1,3>,<2,3>}
3. Отношение строгого порядка (антирефлексивно, антисимметрично, транзитивно)
 (<) X = {1,2,3}
(<) X = {1,2,3}
 = {<1,2>,<1,3>,<2,3>}
= {<1,2>,<1,3>,<2,3>}
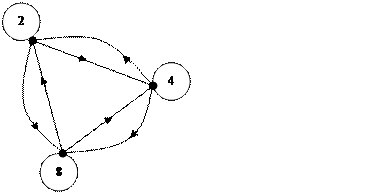
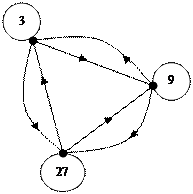
Важнейший признак отношения эквивалентности – оно разбивает элементы множества, на котором берется отношение, на взаимнонепересекающиеся классы, которые называются классами эквивалентности.
Пример:
X = {2,3,4,8,9,27},  – иметь общие знаменатели ≠ 1
– иметь общие знаменатели ≠ 1
 = {<2,2>,<3,3>,<4,4>,<8,8>,<9,9>,<27,27>,<2,4>,<4,2>,<2,8>,<8,2>,<4,8>,
= {<2,2>,<3,3>,<4,4>,<8,8>,<9,9>,<27,27>,<2,4>,<4,2>,<2,8>,<8,2>,<4,8>,
<8,4>,<3,9>,<9,3>,<3,27>,<27,3>,<9,27>,<27,9>}
A1={2,4,8}; A2={3,9,27};
| <== предыдущая страница | | | следующая страница ==> |
| Правила использования зданий на мероприятиях Полигона | | | Функциональные отношения |
Дата добавления: 2014-11-08; просмотров: 285; Нарушение авторских прав

Мы поможем в написании ваших работ!