Логика высказываний

Математическая логика исследует формальные законы построения суждений и доказательств, используя язык, который позволяет описывать ситуацию формально, так чтобы можно было произвести анализ ситуации, т.е. строить и формально доказывать утверждения о свойствах ситуации. Логика исследует схемы рассуждений, которые верны единственно в силу своей формы, абстрагируясь от содержания объектов анализа. Математическая логика – это множество правил манипулирования формулами, представляющими формы рассуждений. Формальная логика строит формальные модели предложений естественного языка, игнорируя их содержание.

Логика выражает формы мышления и способы их выражения в языке. Формальная математическая логика решает проблемы проверки правильности рассуждений в естественном языке (реальный мир), строя свои модели и правила их преобразования. Для этого логика вводит свои языки – систему формальных обозначений (формулы) и правила их преобразования. Поэтому математическую логику можно рассматривать как множество правил манипулирования формулами, описывающими утверждения естественного языка. В результате конкретизации (интерпретации) результатов и выводов формальной логики – новых полученных формул, получаются новые предложения естественного языка, позволяющие оценить свойства исходных предложений и т.д. Следует, однако, ясно понимать, что выводы, полученные с помощью формализма математической логики (как и с помощью любого формализма), можно использовать в реальной жизни не всегда, а только если выполнены ограничения, обеспечивающие адекватность применяемой модели.

Из всего разнообразия конструкций естественного языка логика высказываний имеет дело только с узким кругом утверждений, которые могут принимать значение в множестве {0,1}, где 1 и 0 имеют смысл t (true - истина) и f (false – ложь) соответственно. Высказывания – это переменные, принимающие значения в этом множестве. Они называются атомами. Два атома называются противоположными, если один из них является отрицанием другого: НЕ ИСТИНА – это ЛОЖЬ, НЕ ЛОЖЬ – это ИСТИНА. Кроме простейших высказываний, структура которых не анализируется, рассматриваются формулы. Формула U над множеством атомов строится с использованием логических связок: одноместной Ø, двуместных ®, &, Ú, Å, «, |, ¯ и скобок. Логические связки – это элементарные булевы функции, определение которых дается в теории булевых функций. Формула логики высказываний определяется индуктивно следующими двумя пунктами. Первый из этих пунктов является базисом индукции. В нем непосредственно сообщается, какие комбинации символов следует считать формулами. Второй пункт представляет собой порождающее правило. Предполагается, что все формулы языка L построены последовательным применением правил, сформулированных во втором пункте, к формулам, определенным первым пунктом. Итак:

· любой атом из алфавита А есть формула,

· если P,Q – формулы, то (P®Q), (P&Q), (PÚQ) – формулы,

· (ØР) – также формула,

· других формул нет.

В логике высказываний особое место занимает множество {Ø,®}, образующее функционально полную в Р2 систему функций (базис Фреге). Остальные логические связки могут быть определены как суперпозиции над множеством {Ø,®}. Любое слово в алфавите логики высказываний является формулой, если оно удовлетворяет данному выше определению формулы.

Задачей логики высказываний является определение логического смысла формул. Она решается в соответствии с таблицами истинности связок, используемых при построении формул. Каждая комбинация значений истинности атомов, входящих в формулу, называется интерпретацией. Логика высказываний и теория булевых функций тесно связаны: обе эти формальные модели являются булевыми алгебрами. Будем далее использовать 1 и 0 как символы истины и лжи соответственно.

Таким образом, в логике высказываний определены алфавит, правила образования формул, система аксиом и правил, позволяющих строить новые формулы, т.е. язык логики высказываний образует формальную систему.

В формальной логике тождественно истинными называются формулы, принимающие значение ИСТИНА во всех интерпретациях, т.е. тавтологии. Формула, тождественно ложная во всех интерпретациях, называется невыполнимой. Процедура интерпретации формул логики высказывания определена. Она состоит в построении таблицы истинности для данной формулы.

Аппарат логики высказываний очень похож на формализм теории булевых функций. Однако они решают разные задачи. Задачей теории булевых функций является реализация преобразователей информации, т.е. построение комбинационных схем, реализующих функции. Одной из главных проблем логики, сформулированных еще Аристотелем, является разработка методов определения того, является ли заключительное утверждение истинным при условии истинности приведенных фактов единственно в силу формальной структуры рассуждения, а, не исходя из смысла утверждения и фактов, из которых утверждение построено. Логическое следствие можно считать новым знанием, полученным из уже известных фактов.

Семантика логики высказываний – это смысловая интерпретация ее предложений или формул, которая означает установление соответствия между логическими переменными и объектами окружающей среды. Истинное значение логической переменной (атома) означает наличие соответствующего свойства у объекта, ложное – отсутствие. Определяя значение истинности формул в конкретных интерпретациях, можно судить о наличии у среды совокупности свойств и отношений, выражаемых формулами. Истинностные значения любой формулы, т.е. ее семантику, всегда можно задать таблицей истинности. Однако построение таблиц истинности слишком трудоемко, чтобы можно было с их помощью решать практические задачи. Вместо этого используют специальные правила вывода, применение которых базируется не на понятии общезначимости формулы, а на понятии модели формулы. Понятие модели является важным в логике высказываний, поскольку позволяет ввести понятие выводимости одних истинных формул из других истинных.

Примеры.

1. Если прошел дождь, то дорога мокрая.

В данном утверждении имеется два атома: А – Прошел дождь, и В – Дорога мокрая. Исследуемое утверждение может быть представлено формулой: 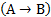. Из житейского опыта мы связываем это причинно-следственное отношение с дополнительным знанием: Если дождя не было, то дорога сухая, т.е. формула 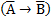также справедлива, ее можно считать следствием исходной формулы. Однако две логические формулы 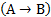и 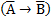различны. Из истинности первой формулы не следует истинность второй.

2. Докажем теорему: «Для того чтобы сепульки не были хроничны и бифуркальны одновременно, необходимо и достаточно, чтобы они были не хроничны или не бифуркальны».

Введя обозначения атомов: x – сепульки хроничны, у – сепульки бифуркальны, представим терему формулой: 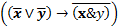. Легко видеть, что посылка и заключение импликации эквивалентны, следовательно, утверждение является тавтологией. Таким образом, для доказательства этой теоремы не нужно ничего знать о сепульках и их свойствах.

Рассмотрим рассуждение: Если бы он не сказал ей, она бы и не узнала. А не спроси она его, он и не сказал бы ей. Но она узнала. Следовательно, она спросила.

В данном рассуждении содержится несколько фактов, которые могут быть представлены как атомы логики высказываний:

· Ск: он сказал ей,

· У: она узнала,

· Сп: она спросила.

Тогда приведенное рассуждение можно записать формулой: .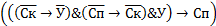

Произведя равносильные преобразования, легко показать, что это тавтология.

Очевидная сентенция: «Истину может сказать всякий»[1]. На языке логики высказываний эту сентенцию можно представить клаузой

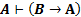
Она означает: «если А истинно, то источником этой истинности может быть все что угодно, например, В». Если произвести эквивалентное преобразование этой клаузы, получим

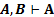
Семантика при этом изменится и станет примерно такой: :»если ранее было установлено. Что А истинно, то истинность В не может проявиться так, что А станет ложным», или «истинность одного высказывания (В) не может повлиять на истинность другого высказывания (А)».

Рассмотрим формальные законы построения умозаключений в естественном языке на примере рассуждения «Спросила – Сказал». Это сложное утверждение представляет собой конъюнкцию трех утверждений, из которых следует некоторый вывод. Выделим в предложениях этого высказывания атомы: Ск, У, Сп и сформулированные ранее утверждения:

· F1 – Если бы он не сказал ей, она бы и не узнала.

· F2 – А не спроси она его, он бы и не сказал ей.

· F3 – Но она узнала.

· R – Следовательно, она спросила.

F1, F2, F3 – факты, R – вывод из этих фактов или заключительное утверждение, являющееся следствием приведенных ранее утверждений.

Справедливость построенного формализма следует из тавтологичности формулы

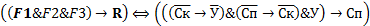
Рассмотрим еще одно рассуждение: “В хоккей играют настоящие мужчины. Трус не играет в хоккей. Я в хоккей не играю. Значит, я трус?”

Элементарными высказываниями здесь будут: Х – Я играю в хоккей, М – Я настоящий мужчина.

Формула, соответствующая этому рассуждению имеет вид:

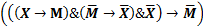
Легко убедиться, что эта формула не является тавтологией. Следовательно, из данных посылок не следует вывод 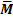Интерпретация (0,1 )аргументов x,m является контрпримером. Такая ситуация означает недостаточность или неточность данных.

В формальной логике разработано несколько методов проверки правильности рассуждений, т.е. проверки того, является ли некоторое утверждение логическим следствием других утверждений. Логическое следствие можно считать новым знанием, полученным из уже известных фактов.

Результаты формальной логики могут быть применены к высказываниям естественного языка, только если выполняются ее постулаты, в частности, высказывания являются только истинными либо ложными («черно-белый мир»), они не включают никаких уровней уверенности - неуверенности, все причинно-следственные отношения между фактами явно выражены, истинностные значения высказываний не меняются во времени. Представляемая здесь логика формализует лишь самую простую часть тех закономерностей, которым подчиняются мышление и язык. Однако даже эта часть является удивительной и впечатляющей по своим результатам. Существуют различные расширения классической логики, например, многозначная логика, формализующая конкретный набор степеней уверенности в истинности высказываний; нечеткая логика, в которой можно оперировать с оценками степеней уверенности (вероятностями) в истинности высказываний; темпоральная логика, позволяющая оперировать высказываниями о свойствах систем, изменяющихся во времени. Эти логики не являются предметом нашего рассмотрения.

Описанные выше примеры являются иллюстрацией применения формальных законов для построения умозаключений естественного языка. Другим примером правильных схем рассуждений являются силлогизмы.

Силлогизмы – это правильные схемы рассуждений. Впервые силлогизмы исследовались еще Аристотелем и имели фиксированную форму, описываемую предикатами (отношениями). В общем смысле силлогизмом называется схема рассуждений из некоторого множества таких схем, в которых заключение всегда верно в силу именно формы рассуждения, а не его содержания. Наиболее часто используемым силлогизмом является правило Modus Ponens (правило отделения), которое записывают в виде: 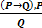Последняя форма записи принята в математической логике и означает, что из истинности формул записанных над чертой, следует истинность формулы, записанной под чертой. Правило Modus Ponens означает, что из истинности импликации P®Q и посылки P следует истинность заключения импликации Q.

Рассуждения, построенные по схеме силлогизмов, правильны именно в силу своей структуры.

Определение 1. Формула R называется логическим следствием формулы Ф (иначе формула R логически следует из множества формул Ф в записи 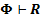) тогда и только тогда, когда для всякой интерпретации, в которой формула Ф истинна, R также истинна.

Очевидно, любая формула является следствием самой себя. Это следует из таблицы истинности импликации: . С другой стороны, из ложных фактов можно вывести любое утверждение. Например, знаменитый пример Гилберта: Если 2×2=5, то Луна сделана из зеленого сыра - с точки зрения логики является совершенно правильным умозаключением.

Определение 2. Формула R называется логическим следствием формул F (это можно записать в виде: F 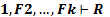) тогда и только тогда, когда для всякой интерпретации, в которой истинна конъюнкция F 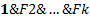, формула R также истинна.

Истинность конъюнкции F 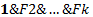нескольких фактов является логическим следствием истинности этих фактов.

Инспектора Крейга из Скотланд-Ярда направили для проверки лечебницы для умалишенных. Каждый из обитателей лечебницы - врач либо пациент – мог быть либо здоров, либо лишен рассудка. Если он был здоров, он говорил правду, если лишен рассудка, то только лгал. В лечебнице Крейг побеседовал с двумя обитателями, Джоном и Смитом. Джон сказал, что Смит – один из врачей больницы, а Смит сказал, что Джон – пациент. Поразмыслив, Крейг догадался, что либо в клинике есть доктора, лишенные рассудка, либо пациенты, которые нормальны. Очевидно, то и другое следует пресекать. Как он догадался об этом?

Введем обозначения: x –Джон - доктор, y –Смит – доктор.

Тогда –Джон – пациент, 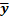–Смит – пациент. Информация, полученная Крейгом, сводится к четырем фактам:

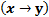– (если Джон нормален, то Смит – доктор),

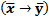– (если Джон - пациент, то Смит – пациент),

– (если Смит - доктор, то Джон – пациент),

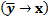– (если Смит - пациент, то Джон – доктор).

Если множество этих фактов непротиворечиво, то их конъюнкция истинна. Выполнив элементарные преобразования, получаем подтверждение противоречивости множества указанных высказываний:

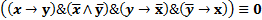
Следовательно, множество утверждений, которые могут быть сформулированы на основе полученной Крейгом информации, является противоречивым и на основании этой информации можно сделать любой вывод о положении дел в лечебнице. Поэтому у инспектора Крейга есть все основания для того, чтобы назначить расследование.

Следуя Определению 2 логического вывода, истинность утверждения можно подтвердить также с помощью таблицы истинности булевой функции, моделирующей это рассуждение. Например, таблица истинности для первого примера («Спросила – сказал») имеет вид:)

Таблица 1 Доказательство логического следствия

Ск	Сп	У	F1=ØСк®ØУ	F2=ØСп®ØСк	F3=У	F	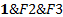R=Сп	F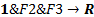

Следовательно, в схеме рассуждений «Спросила – Сказал» вывод с необходимостью следует из истинности фактов.

Однако при большом числе атомов такие таблицы становятся очень громоздкими и в логике высказываний для доказательства истинности вывода используют другие методы.

Пусть мы имеем произвольную систему рассуждений. Определение логического следствия дает основание для систематической проверки правильности любой схемы рассуждений. Построим таблицы истинности для всех утверждений рассмотренной выше задачи «Спросила – Сказал».

Дата добавления: 2014-11-08; просмотров: 1211; Нарушение авторских прав

Мы поможем в написании ваших работ!