Формальные модели

Формальные системы

Логика представляет собой науку о способах рассуждений. Математическая логика – это математическая дисциплина, которая изучает способы рассуждений, применяемые в математике, средствами самой математики.

Формальные модели позволяют адекватно отображать разнообразные предметные области и операции, применяемые при манипулировании данными. Методология таких моделей разрабатывается в формальных системах.

В формальной логике разрабатываются методы правильных рассуждений, представляющих собой цепь умозаключений в логически последовательной форме. Рассуждения в ней изучаются с точки зрения формы, а не смысла.

В формальной логике не рассматривается семантика предложений. Это является результатом применения операции абстрагирования к рассуждениям естественного языка. Абстрагирование широко используется в науке для исследования различных аспектов рассматриваемой проблемы. Современная парадигма научного исследования состоит в том, что формальное изучение любой проблемы начинается с замены реальных объектов их абстрактными представлениями (моделями), в которых отражены именно те свойства исходных объектов, которые мы хотим изучать. Абстрагирование позволяет строить формальные модели понятий, процессов и явлений реального мира и далее изучать их с помощью формальных же средств. Именно на основе научного подхода к решению инженерных проблем получены многие впечатляющие результаты в технике, в связи с чем давно укоренилась поговорка «Нет ничего практичнее хорошей теории».

Основными задачами формальной логики являются выявление противоречий в рассуждениях и изучение отдельных этапов рассуждений или выводов, когда строго шаг за шагом доказывается их правильность независимо от используемой интерпретации.

Формальная система представляет собой совокупность чисто абстрактных объектов (не связанных с внешним миром), в которой представлены правила оперирования множеством символов в чисто синтаксической трактовке без учета смыслового содержания.

Формальная система определена, если:

· задан конечный алфавит.

· определена процедура построения формул.

· выделено некоторое множество формул, называемых аксиомами.

· задано конечное множество правил вывода, которые позволяют получать новые формулы из уже имеющихся формул и аксиом.

Пусть дано множество А, называемое алфавитом. Словом длины m над алфавитом А называется кортеж 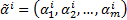, где 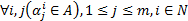., в котором буквы могут повторяться. Число букв m в слове называется длиной слова.

Правильно построенное слово в алфавите А называется формулой.

Процесс формирования истинных слов в формальной теории состоит в следующем: выделяется некоторое множество слов, которые называются аксиомами теории, и указывается конечное множество отношений P между словами. Отношения между словами называются правилами вывода.

Выводом в формальной теории называется всякая последовательность слов 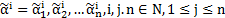, такая, что для всех i,j слово 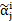есть либо аксиома, либо получено из какого-нибудь предыдущего слова по правилам вывода. Непосредственным следствием слова 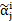, 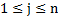по правилу P называется слово 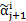, если существует отношение .

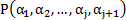Слово 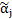выводимо, если существует вывод в формальной теории, в котором это слово является последним. Такой вывод называется доказательством. В этом случае слово 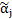является теоремой формальной теории. В частности всякая аксиома является теоремой. Если формула Т является теоремой, это обозначают: 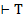, читается: выводима .

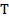Теоремой является любое высказывание, присутствующее в доказательстве.

Множество формул формальной системы вместе с множеством аксиом и правил вывода образуют формальный язык L. Формальный язык отличается от естественного тем, что его конструкции строятся по строго определенным правилам и не допускают двусмысленного толкования.

Под формальной теорией понимают множество слов языка L с выделенным в нем подмножеством истинных слов.

Построенная указанным способом формальная теория называется аксиоматической формальной теорией, исчислением или дедуктивной системой.

Говорят, что существует интерпретация формальной теории в содержательную, если имеется соответствие между словами формальной теории и объектами-утверждениями содержательной теории.

Формальную теорию, в которой понятие вывода определено указанным выше способом, называют каноническим исчислением Поста.

Дата добавления: 2014-11-08; просмотров: 432; Нарушение авторских прав

Мы поможем в написании ваших работ!