Классическое исчисление высказываний

Логическим исчислением, или просто исчислением, называется формальная система, в которой определены алфавит, правила построения формул, некоторое множество аксиом и правил вывода. Аксиомы и правила вывода позволяют строить новые формулы, которые являются общезначимыми, т.е. также являются аксиомами или теоремами. Правила вывода применяются непосредственно к формулам, а не к таблицам истинности. Исчисление высказываний может включать много аксиом и мало правил вывода, тогда оно образует аксиоматическую формальную систему или классическое исчисление высказываний.

Логика высказываний, или пропозициональная логика (propositio — «высказывание»), или исчисление высказываний—изучает сложные, образованные из простых, и их взаимоотношения. В отличие от логики предикатов, внутренняя структура простых высказываний не рассматривается, а учитывается лишь, с помощью каких союзов и в каком порядке простые высказывания сочленяются в сложные.

Несмотря на свою важность и широкую сферу применения, логика высказываний является простейшей логикой и имеет очень ограниченные средства для исследования суждений.

Логика высказываний является теорией тех логических связей высказываний, которые не зависят от внутреннего строения (структуры) простых высказываний.

Логика высказываний исходит из следующих двух допущений:

1) всякое высказывание является либо истинным, либо ложным (принцип двузначности);

2) истинностное значение сложного высказывания зависит только от истинностных значений входящих в него простых высказываний и характера их связи.

На основе этих допущений ранее были даны строгие определения логических связок «и», «или», «если, то» и др. Эти определения формулировались в виде таблиц истинности и назывались табличными определениями связок. Соответственно, само построение логики высказываний, опирающееся на данные определения, называется табличным её построением.

Язык логики высказываний (пропозициональный язык) искусственный язык, предназначенный для анализа логической структуры сложных высказываний.

Алфавит языка логики высказываний

Исходные символы, или алфавит языка логики высказываний, разделены на следующие три категории:

· пропозициональные буквы (пропозициональные переменные):

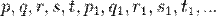
· логические знаки (логические союзы): , , , , ;

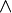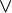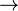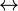· технические знаки: 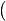— левая скобка, 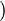— правая скобка.

· Других знаков в алфавите языка логики высказываний нет.

Пропозициональные переменные

Пропозициональная переменная — переменная, которая в пропозициональных формулах служит для замены собой элементарных логических высказываний.

Пропозициональные формулы

Роль структурных образований, аналогичных элементарным и сложным высказываниям, играют в этом языке формулы. Пропозициональная формула — конечная последовательность знаков алфавита, построенная по изложенным ниже правилам и образующая законченное выражение языка логики высказываний. Заглавные латинские буквы 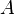, , … употребляются для обозначения формул. Индуктивное определение формулы логики высказываний:

· пропозициональная переменная есть формула;

· если 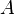— произвольная формула, то 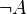— тоже формула;

· есл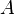и и — произвольные формулы, то 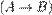, , 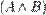, 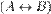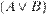и 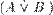— тоже формулы;

· Других формул в языке логики высказываний нет.

Относительно любой последовательности знаков алфавита языка логики высказываний можно решить, является она формулой или нет. Если эта последовательность может быть построена в соответствии с определением формулы, то она формула, если нет, то не формула.

Язык логики высказываний можно рассматривать как множество пропозициональных формул.

Для формул логики высказываний можно определить понятие интерпретации как приписывание каждой пропозициональной переменной истинностного значения («истина» или «ложь», хотя исчисление высказываний никак не ограничивает множество возможных значений при интерпретации: например, можно задать интерпретацию как отображение в множество 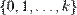, где .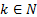

Соглашения о скобках

Поскольку в построенных по определению формулах оказывается слишком много скобок, иногда и не обязательных для однозначного понимания формулы, математики приняли соглашения о скобках, по которым некоторые из скобок можно опускать. Записи с опущенными скобками восстанавливаются так:

· Если опущены внешние скобки, то они восстанавливаются.

· Если рядом стоят две конъюнкции или дизъюнкции (например, 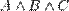), то в скобки заключается сначала самая левая часть (то есть две подформулы со связкой между ними). (Говорят также, что эти связки левоассоциативны.)

· Если рядом стоят разные связки, то скобки расставляются согласно приоритетам: 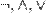и 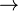(от высшего к низшему).

Когда говорят о длине формулы, имеют в виду длину подразумеваемой (восстанавливаемой) формулы, а не сокращённой записи. (Следовательно, длина формулы языка PL – это число символов в ее записи, включая скобки, в том числе, внешние.)

Например, запись 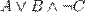означает формулу 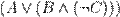, а её длина равна 12.

Дата добавления: 2014-11-08; просмотров: 602; Нарушение авторских прав

Мы поможем в написании ваших работ!