Семантические таблицы

Методы доказательств – это алгоритмические процедуры, следуя которым, можно установить, является ли формула тавтологией, и выполнимо ли множество формул.

В 1934 немецкий математик Генцен (1909-1945) доказал существование алгоритмических процедур, позволяющих установить тавтологичность формул, применяя сформулированные им правила вывода. Эти правила стали основой исчисления высказываний.

Используя теорию доказательства, Бет и Хинтика в 1955 г. предложили алгоритм, устанавливающий, является ли составное высказывание тавтологией или нет, получивший название метода семантических таблиц Бета.

При помощи семантических таблиц Бета можно исследовать значение истинности данного высказывания без построения таблицы истинности, которая строится в теории булевых функций. Семантическая таблица – это дерево, вершинами которого является исследуемая формула и все ее подформулы. Вершина называется особой, если она отлична от атома, т.е. ее логическое значение зависит от последней выполняемой логической связки. Вершина называется обычной, если в ней находится атом. Последние вершины каждой ветви – это обязательно атомы, и такие вершины называются листьями. Семантическая таблица составного высказывания К строится индуктивно, исходя из семантических таблиц подформул, входящих в высказывание К. Каждой логической связке, выполняемой в соответствующей данной вершине подформуле, сопоставляется элементарная семантическая таблица в виде дерева, раскрывающего логическую интерпретацию связки. Примеры наиболее употребимых в логике высказываний связок приведены на рис. 1.

Рисунок 1 Элементарные семантические таблицы

Идея метода основывается на построении дерева, вершинами которого являются все подформулы данной формулы. Логическое значение всех подформул исследуется вплоть до атомов, называемых листьями, пока не будет обнаружено противоречие в данной ветви или в данной ветви не останется особых вершин. Такое дерево воспроизводит таблицу истинности формулы. Однако часто нет необходимости строить все дерево до листьев: в некотором узле значение функции может быть определено сразу для всех листьев, которые могут быть построены из этого узла.

Пусть К–формула языка логики высказываний. Обозначим tK утверждение «К - истинно» и fK - утверждение: «К-ложно». При этом tK и fK называются помеченными формулами.

Семантическая таблица – это дерево, вершинами которого являются помеченная формула и ее помеченные подформулы.

Атомарные семантические таблицы – это семантические таблицы для элементарных булевых функций {&, Ú, ®, «, Ø, …}. Примеры атомарных семантических таблиц для произвольных формул s1 и s2 представлены на Рис. 1.

Семантическая таблица составного высказывания К – это граф, не имеющий циклов (дерево), с единственным корнем, в который помещается помеченная формула К. Каждая ветвь дерева интерпретируется как конъюнкция всех подформул, записанных в вершинах этой ветви. Семантическая таблица строится сверху вниз, исходя из индуктивного правила определения формулы: неделимые высказывания (литералы) – это атомы; из атомов строятся формулы с использованием логических связок. Каждая формула является результатом применения одно- или двухместной логической связки к образующим ее подформулам. Для этих связок выше определены атомарные семантические таблицы.

Процедура построения семантической таблицы состоит в следующем:

· Построение семантической таблицы для составного высказывания начинаем с того, что записываем помеченную формулу tK или fK в корень семантической таблицы.

· Если какая-то часть таблицы уже построена, находим в множестве висячих вершин (т.е. вершин графа, которым инцидентно единственное ребро) особые вершины и продолжаем построение атомарными семантическими таблицами для каждой из подформул. Вершина семантической таблицы называется особой, если она встречается как корень некоторой атомарной семантической таблицы. Если вершина обозначена помеченным атомом, она называется обычной.

· Ветвь семантической таблицы называется противоречивой, если в ней встречаются обычные вершины, содержащие помеченные атомы tP и fP, которые означают, что конъюнкция всех подформул, входящих в данную вервь равна нулю. Т.е. эта ветвь содержит противоречие, обусловленное атомом P на некотором наборе значений пропозициональных переменных решаемой задачи.

· Семантическая таблица называется замкнутой, если ни одна из ее ветвей не содержит особых вершин, которые не были бы продолжены в соответствии с атомарными семантическими таблицами ее подформул. В противном случае семантическая таблица называется незамкнутой.

· Семантическая таблица противоречива, если каждая ее ветвь противоречива. Если замкнутая семантическая таблица с корнем fK противоречива, а это означает, что мы пытались всеми возможными способами сделать высказывание К ложным и не сумели, то К – тавтология.

· Доказательством или выводом по Бету высказывания К называется замкнутая противоречивая семантическая таблица, в корне которой помещена помеченная формула fK.

· Замкнутая противоречивая таблица, имеющая в качестве корня tK, называется опровержением по Бету высказывания К.

· Говорят, что высказывание К доказуемо или выводимо по Бету, если оно имеет доказательство по Бету. Высказывание называется опровержимым по Бету, если существует опровержение К по Бету. Факт, что К доказуемо по Бету обозначается .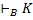

В данном случае понятие выводимости отличается от аналогичного определения в теории булевых функций и означает общезначимость рассуждения. Чтобы избежать путаницы понятий, будем применять для обозначения тождественной истинности высказываний термин доказуемо.

Рассмотрим пример построения семантической таблицы Бета для доказательства истинности высказывания

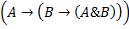
В корень дерева поместим формулу, пометив ее как ложную (f). Раскрывая последовательно значения всех ее подформул с помощью элементарных семантических таблиц для логических связок 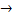и &, будем строить ветви дерева сверху вниз до тех пор, пока в каждой ветви не обнаружится противоречие в виде входящего в ветвь одного и того же атома, помеченного однажды как истина(t) и другой раз как ложно ()f. Как только противоречие обнаружится, дальнейшее построение ветви прекращается.

Построение таблицы очевидно из Рис. 2.

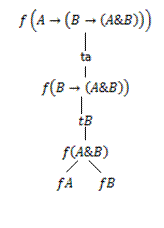
Рисунок 2. Доказательство методом семантической таблицы Бета

Дата добавления: 2014-11-08; просмотров: 1947; Нарушение авторских прав

Мы поможем в написании ваших работ!