Интерпретация языка логики высказываний

Основной задачей логики высказываний является установление истинностного значения формулы, если даны истинностные значения входящих в неё переменных. Истинностное значение формулы в таком случае определяется индуктивно (с шагами, которые использовались при построении формулы) с использованием таблиц истинности связок.

Тождественно истинные формулы (тавтологии)

Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных (то есть, при любой интерпретации). Вот несколько широко известных примеров тождественно истинных формул логики высказываний:

Законы де Моргана:

1) ;

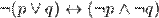2) ;

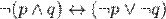Закон контрапозиции:

;

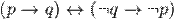Законы поглощения:

1) ;

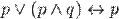2) ;

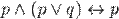Законы дистрибутивности:

1) ;

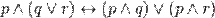2) .

Дата добавления: 2014-11-08; просмотров: 481; Нарушение авторских прав

Мы поможем в написании ваших работ!