
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Программная модель ALU-1
Программная модель ALU-1 включает две составные части – операционный автомат 8-разрядного двоичного арифметико-логического устройства и управляющий автомат с программируемой логикой, который может работать как автономно, так и взаимодействуя с операционным автоматом.
1.1.1. Операционный автомат арифметико-логического устройства ALU-1
Рассматриваемая структура операционного автомата почти универсальна и позволяет реализовать большинство известных алгоритмов арифметических преобразований. Операционный автомат предназначен для реализации арифметических операций над двоичными числами, представленными
в 8-разрядном формате с фиксированной запятой в беззнаковой и знаковой формах (диапазоны представления чисел – от 0 до 255 и от –127 до 127 соответственно), а также для реализации логических операций над 8-разрядными двоичными числами.
Операционный автомат позволяет с помощью микропрограмм реализовать следующие арифметические операции:
■ сложение и вычитание в беззнаковой форме;
■ сложение и вычитание в прямом, обратном или дополнительном двоичном коде;
■ умножение в беззнаковой или знаковой форме;
■ деление в беззнаковой или знаковой форме без восстановления остатка или с восстановлением остатка.
Кроме того, операционный автомат позволяет реализовать следующие поразрядные логические операции:
■ отрицание («НЕ»);
■ конъюнкция («И»);
■ дизъюнкция («ИЛИ»);
■ неравнозначность (исключающее «ИЛИ»).
Из приведенного списка следует, что возможно реализация и других, более сложных арифметических и логических операций.
Результатом выполнения всех арифметических и логических операций, за исключением умножения, является 8-разрядное число в формате, совпадающим с форматом исходных данных. Результат умножения может быть представлен как в 8-, так и в 16-разрядном формате.
На рис. 1.1 представлена структура операционного автомата в том виде, в котором она выводится на экран компьютера программой, поддерживающей процесс разработки микропрограмм управления выполнением операций для АЛУ.
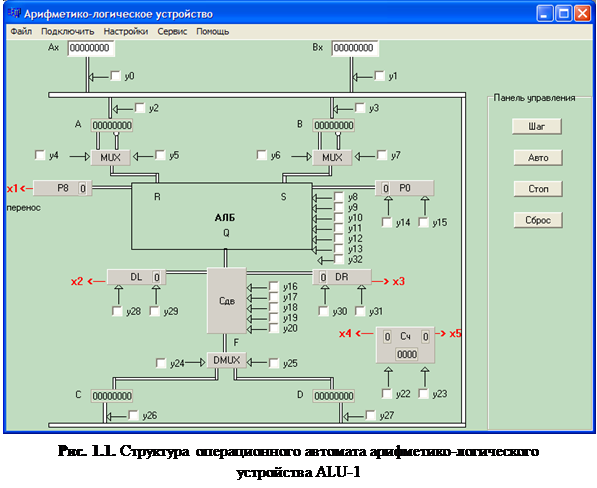
Операционный автомат содержит следующие элементы:
■ входные 8-разрядные регистры Ax и Bx, допускающие загрузку исходных операндов из файла;
■ 8-разрядные регистры A и B операндов;
■ 8-разрядный арифметико-логический блок АЛБ с триггерами входного P0 и выходного P8 переносов (заемов);
■ два 8-разрядных двухвходовых мультиплексора MUX, выбирающих для входов R и S АЛБ прямые или инверсные значения из регистров A и B соответственно;
■ триггер Z (на рис. 1.1 явно не показан), значение которого формируется в соответствии с выражением
Z = P8 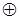 DL
DL
и используется для формирования цифры частного в некоторых алгоритмах деления;
■ блок сдвига, включающий 8-разрядный реверсивный комбинационный элемент Сдв, выполняющий сдвиг, и два триггера – DL и DR, формирующие или принимающие данные слева и справа соответственно;
■ два 8-разрядных регистра результата C и D;
■ демультиплексор DMUX, передающий значение 8-разрядного слова F с выхода блока сдвига в один из регистров результата (C или D);
■ 4-разрядный двоичный счетчик Сч;
■ 8-разрядную шину, на которую могут быть переданы слова из регистров Ax, Bx, C, D и с которой поступают в регистры A и/или B.
Регистры сами по себе никаких функциональных преобразований кодов не выполняют. Они являются лишь устройствами памяти, подключенными к общей шине. Входные регистры Ax, Bx и выходные регистры C, D могут находиться в одном из трех устойчивых состояний, которые позволяют подключать выходы регистра к шине или отключать их от шины. Если не принимать во внимание физические аспекты, то шину можно рассматривать как совокупность восьми переменных, каждая из которых может принимать одно из трех значений – «не активна», 0 или 1.
В рассматриваемой версии модели ALU-1 арифметико-логического устройства возможна лишь передача в рабочие регистры A, B содержимого регистров Ax, Bx, C, D. При этом за один такт можно выполнить передачу только из одного регистра-источника в регистр A, в регистр B или в оба регистра одновременно. Для этого выполняется одна из четырех микроопераций y0, y1, y26, y27, подключающая к шине выводы соответствующего регистра-источника, а также микрооперация y2 или y3 (или обе одновременно), передающая состояние шины на входы регистров-приемников (см. рис. 1.1).
Очевидно, что одновременное подключение к шине двух регистров-источников приводит к конфликту данных, поэтому оно является недопустимым. Одновременная же запись информации с шины в разные регистры-приемники, напротив, допустима. Однако такая необходимость редко встречается при реализации конкретных алгоритмов.
Арифметико-логический блок АЛБ содержит комбинаторную схему функционального преобразователя и два элемента памяти – триггеры P0 и P8. Состояние триггера P0 может быть задано произвольно с помощью микроопераций y14 и y15. В дальнейшем оно участвует в микрооперациях сложения (вычитания) в качестве значения переноса (заема) младшего разряда. Триггер P8 изменяется только микрокомандами арифметических и логических микроопераций АЛБ. При выполнении арифметических микроопераций он принимает значение переноса либо заема, возникающего из старшего разряда. При выполнении логических микроопераций триггер всегда устанавливается в «0». Остальные микрооперации сохраняют ранее установленное значение P8.
Арифметико-логический блок реализует ряд бинарных операций
над 8-разрядными двоичными словами R и S и битом P0. Результат операции записывается в 8-разрядное слово Q и бит P8. При этом значение P8 рассматривается как логическое условие x1, формируемое операционным автоматом. Кроме того, в блоке АЛБ формируется значение логического условия x6 = P8 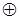 DL, для отображения которого необходимо выполнить команду меню Настройки ► Z:=p8 (+) DL.
DL, для отображения которого необходимо выполнить команду меню Настройки ► Z:=p8 (+) DL.
Арифметико-логический блок реализует следующие бинарные микрооперации (y8, y9, y10, y11, y12, y13):
P8.Q = R + S + P0, P8.Q = R – S – P0,
P8.Q = S – R –P0, 0.Q = R & S,
0.Q = R ˅ S, 0.Q = R 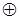 S.
S.
Кроме того, АЛБ реализует унарную микрооперацию P8.Q = P8.R (y32), в результате выполнения которой значение P8 не изменяется.
Блок сдвига содержит собственно элемент реверсивного сдвига Сдв на один разряд и два триггера данных – «слева» DL и «справа» DR. Каждый из этих триггеров может быть установлен с помощью микроопераций y28, y29, y30, y31 таким образом, чтобы он мог принять значения разрядов, теряемых при выполнении сдвига слова Q. Текущие значения триггеров DL и DR могут рассматриваться как значения логических условий x2 и x3 соответственно.
При сдвиге вправо младший разряд Q0 сдвигаемого слова Q записывается в триггер DR, а в старший разряд F7 выходного слова F помещается значение, предварительно установленное во триггере DL. При этом состояние самого триггера DL не изменяется. При сдвиге влево, наоборот, выполняются операции
DL = Q7, F0 = DR, DR = DR.
Элемент сдвига Сдв позволяет преобразовать входное слово Q в выходное слово F и без сдвига. При этом значения триггеров DL и DR не изменяются.
Таким образом, блок сдвига выполняет следующие микрооперации (y16, y17, y18, y19, y20):
■ F7:0 = Q7:0 – передача без сдвига;
■ F7:0.DR = DL.Q7:0 – обыкновенный сдвиг вправо;
■ DL.F7:0 = Q7:0.DR – обыкновенный сдвиг влево;
■ F7:0.DR = DR.Q7:0 – специальный сдвиг вправо;
■ F7:0 = Q6:0.НЕ(Z) – специальный сдвиг влево.
Специальный сдвиг вправо удобно использовать в микропрограмме умножения при формировании 16-разрядного произведения, а специальный сдвиг влево – в микропрограмме деления при формировании очередной цифры частного.
Четырехразрядный двоичный счетчик Сч реализует две микрооперации – y22 (начальная установка счетчика в состояние «0000») и y23 (инкремент). Он принимает последовательные значения от 0000 до 1000. Счетчик формирует два логических условия – x4 и x5. Логическое условие x4 истинно, если счетчик находится в состоянии 1000, а логическое условие x5 истинно, если состояние счетчика больше, чем 0011.
Назначение мультиплексоров MUX и демультиплексора DMUX очевидным образом следует из структурной схемы операционного автомата, представленной на рис. 1.1.
Полные списки микроопераций, реализуемых в операционном автомате ALU-1, и формируемых в нем логических условий приведены в табл. 1.1 и 1.2 соответственно.
Таблица 1.1
Микрооперации, реализуемые в операционном автомате ALU-1
| Обозначение | Микрооперация | Описание микрооперации |
| y0 | Shina = Ax | Подключение выходов регистра Ax к шине данных |
| y1 | Shina = Bx | Подключение выходов регистра Bx к шине данных |
| y2 | A = Shina | Запись в регистр A значения из регистра, подключенного к шине |
| y3 | B = Shina | Запись в регистр B значения из регистра, подключенного к шине |
| y4 | R = A | Подключение прямых выходов элементов регистра A к входу R АЛБ. При отсутствии микрокоманды подключения на вход R подаются нулевые значения |
| y5 | R = НЕ(A) | Подключение инверсных выходов элементов регистра A к входу R АЛБ |
| y6 | S = B | Подключение прямых выходов элементов регистра B к входу S АЛБ. При отсутствии микрокоманды подключения на вход S подаются нулевые значения |
| y7 | S = НЕ(B) | Подключение инверсных выходов элементов регистра B к входу S АЛБ |
продолжение табл. 1.1
| Обозначение | Микрооперация | Описание микрооперации |
| y8 | P8.Q = R + S + P0 | Сложение чисел, находящихся на входах R, S, а также содержимого триггера P0 АЛБ. Содержимое триггера P0 добавляет 0 или 1 к младшему разряду суммы, а в триггере P8 формируется значение переноса |
| y9 | P8.Q = R - S - P0 | Вычитание из числа, находящегося на входе R, числа, находящегося на входе S, а также содержимого триггера P0 АЛБ. Содержимое триггера P0 вычитается из младшего разряда разности, а в триггере P8 формируется значение заема старшего разряда |
| y10 | P8.Q = S - R - P0 | Вычитание из числа, находящегося на входе S, числа, находящегося на входе R, а также содержимого триггера P0 АЛБ. Содержимое триггера P0 вычитается из младшего разряда разности, а в триггере P8 формируется значение заема старшего разряда |
| y11 | 0.Q = S & R | Поразрядная конъюнкция чисел, находящихся на входах R и S АЛБ. В триггер P8 помещается 0 |
| y12 | 0.Q = S ˅ R | Поразрядная дизъюнкция чисел, находящихся на входах R и S АЛБ. В триггер P8 помещается 0 |
| y13 | 0.Q = S 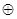 R R
| Поразрядная неравнозначность чисел, находящихся на входах R и S АЛБ. В триггер P8 помещается 0 |
| y14 | P0 = 0 | Установка триггера P0 в состояние 0 |
| y15 | P0 = 1 | Установка триггера P0 в состояние 1 |
| y16 | F = Q | Передача слова Q с выхода АЛБ на выход F схемы сдвига без изменений |
| y17 | F7:0.DR = DL.Q7:0 | Обыкновенный сдвиг слова Q с выхода АЛБ вправо. Младший разряд слова Q помещается в триггер DR. В старший разряд слова F помещается содержимое триггера DL. Содержимое триггера DL не изменяется |
| y18 | DL.F7:0 = Q7:0.DR | Обыкновенный сдвиг слова Q с выхода АЛБ влево. Старший разряд слова Q помещается в триггер DL. В младший разряд слова F помещается содержимое триггера DR. Содержимое триггера DR не изменяется |
| y19 | F7:0.DR = DR.Q7:0 | Специальный сдвиг слова Q с выхода АЛБ вправо. Младший разряд слова Q помещается в триггер DR. В старший разряд слова F помещается предыдущее значение триггера DR |
| y20 | F7:0 = Q6:0.НЕ(Z)
Z = P8 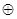 DL DL
| Специальный сдвиг слова Q с выхода АЛБ влево. Старший разряд слова Q утрачивается. В младший разряд слова F помещается очередная цифра частного (в операциях деления). Содержимое триггера DL не изменяется |
| y21 | Стоп | Останов. Сигнал об окончании выполнения операции |
окончание табл. 1.1
| y22 | Сч = 0 | Инициализация всех разрядов счетчика Сч нулевыми значениями. Установка триггеров признаков x4 и x5 в состояние 0 |
| y23 | Сч = Сч + 1 | Увеличение счетчика на 1. При значении счетчика Сч = 1000 триггер признака x4 устанавливается в состояние 1. При значениях счетчика Сч, равных 0100, 0110, 0111 и 1000 триггер признака x5 устанавливается в состояние 1. Если текущее состояние счетчика Сч = 1000, то при увеличении на 1 он переходит в состояние 0000 и оба триггера признаков устанавливаются в состояние 0 |
| y24 | C = F | Помещение слова F на выходе схемы сдвига в регистр C |
| y25 | D = F | Помещение слова F на выходе схемы сдвига в регистр D |
| y26 | Shina = C | Подключение выходов регистра C к шине данных |
| y27 | Shina = D | Подключение выходов регистра D к шине данных |
| y28 | DL = 0 | Установка триггера DL в состояние 0 |
| y29 | DL = 1 | Установка триггера DL в состояние 1 |
| y30 | DR = 0 | Установка триггера DR в состояние 0 |
| y31 | DR = 1 | Установка триггера DR в состояние 1 |
| y32 | Q = R | Передача слова R с входа АЛБ на выход Q без изменений |
Таблица 1.2
Логические условия, формируемые операционным автоматом ALU-1
| Обозначение | Логическое условие | Описание логического условия |
| x1 | P8 | Признак переноса или заема |
| x2 | DL | Состояние триггера DL |
| x3 | DR | Состояние триггера DR |
| x4 | Сч = 1000 | Значение счетчика Сч равно 8 |
| x5 | Сч > 0011 | Значение счетчика Сч больше 3 |
| x6 | Z = P8 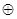 DL DL
| Признак, по которому можно определить значение очередной цифры частного в операциях деления |
Рассмотренная модель операционного автомата может работать в двух режимах – автономно или под управлением микропрограммы, являющейся составной частью модели управляющего автомата.
Автономный режим реализуется только пошагово и позволяет проверить правильность разработанных алгоритмов арифметических и логических преобразований на ряде конкретных примеров.
| <== предыдущая страница | | | следующая страница ==> |
| АРХИТЕКТУРА ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ | | | Управляющий автомат арифметико-логического устройства ALU-1 с программируемой логикой |
Дата добавления: 2014-11-08; просмотров: 548; Нарушение авторских прав

Мы поможем в написании ваших работ!