Управляющий автомат арифметико-логического устройства ALU-1 с программируемой логикой

Предлагаемая модель управляющего автомата ориентирована, прежде всего, на управление операционным автоматом, описанным в разд. 1.1.1. Однако с помощью этой модели можно реализовать и любую «абстрактную» микропрограмму с учетом приведенных далее ограничений.

Управляющий автомат с программируемой логикой реализован как автомат с естественной адресацией и смешанным способом кодирования поля микроопераций и использует единственный формат микрокоманды. Структурная схема моделируемого управляющего автомата аналогична схеме, приведенной на рис. ??. Отличия состоят лишь в количестве микроопераций и их полей, а также в количестве логических условий, поступающих из операционного автомата.

Количественные характеристики управляющего автомата и формат микрокоманды выбирались, прежде всего, исходя из потребностей управления операционным автоматом арифметико-логического устройства ALU-1. Анализ структуры операционного автомата и реализуемых в ней микропрограмм показывает, что можно ограничиться пятью микрооперациями в микрокоманде. Действительно, глядя на рис. 1.1, можно отметить, что для выполнения любой бинарной микрокоманды (например, для арифметического сложения двоичных чисел) необходимо одновременно выполнить следующие операции:

1) выбрать первый операнд R;

2) выбрать второй операнд S;

3) указать операцию, выполняемую арифметико-логическим блоком АЛБ;

4) указать операцию, выполняемую в блоке сдвига;

5) определить регистр, в который следует поместить результат.

Таким образом, все множество 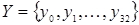следует разбить на пять подмножеств (см. разд. ??) с учетом анализа типичных микропрограмм арифметических и логических операций. Такая работа была проделана при проектировании модели управляющего автомата, и ее результат предлагается в виде кодировки микроопераций По умолчанию (рис. 1.2).

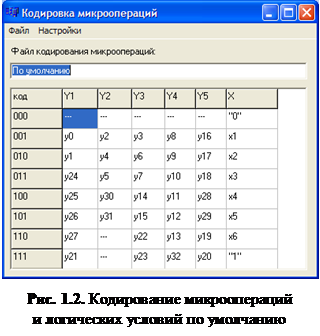
Окно, изображенное на рис. 1.2, можно открыть, выполнив из меню окна Арифметико-логическое устройство команду Подключить ► Управляю­щий автомат. В результате выполнения откроется одноименное окно, из меню которого нужно выполнить команду Кодировка микроопераций.

Практика показывает, что большинство алгоритмов арифметических и логических преобразований можно реализовать в структуре операционного автомата арифметико-логического устройства ALU-1 с предложенным разбиением и кодированием микроопераций. Однако пользователь может произвольно изменять разбиение микроопераций на подмножества и кодирование этих подмножеств (микрокоманд). Для этого нужно из меню окна Кодировка микроопераций выполнить команду Настройки ► Разрешить правку. Однако при этом нельзя увеличивать количество подмножеств, а число микроопераций в одном подмножестве не может быть больше семи. Данные ограничения связаны с жестко определенным форматом микрокоманды.

Формат микрокоманды (рис. 1.3) включает:

■ пять трехразрядных полей 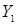, , 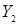, , 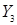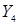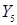кодирования микроопераций;

■ трехразрядное поле 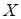номера логического условия (операционный автомат генерирует шесть логических условий, а еще два кода используются для кодирования констант 0 и 1);

■ одноразрядное поле 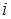инверсии логического условия;

■ семиразрядное поле адреса перехода.

Очевидно, что максимальная длина микропрограммы в этом случае может составлять 2⁷ = 128 микрокоманд.

В разд. ?? приведен пример проектирования управляющего автомата с программируемой логикой по исходной микропрограмме. Процесс проектирования включает следующие этапы:

■ определение формата микрокоманды (разбиение множества микроопераций на подмножества, кодирование микроопераций и логических условий);

■ формирование последовательности управляющих слов в постоянном запоминающем устройстве микрокоманд, реализующих заданную микропрограмму.

Очевидно, что если для построения управляющего автомата с программируемой логикой использовать программную модель ALU-1, то первый этап выполнять не придется при условии, что предложенное «по умолчанию» разбиение позволит реализовать заданную микропрограмму.

Второй этап можно выполнить «вручную» или с помощью встроенного микроассемблера. Работа «вручную» весьма трудоемка и приводит к значительному числу ошибок. Однако на начальном этапе небольшую микропрограмму следует выполнить именно этим способом, чтобы получить полное представление о структуре микрокомандных слов и способах переходов по микропрограмме. Процесс «ручного» микропрограммирования подробно описан в примере из разд. ??.

Использование микроассемблера позволяет значительно увеличить скорость и надежность подготовки микропрограмм. Для работы с микроассемблером необходимо из меню окна Управляющий автомат выполнить команду Компилятор. В результате выполнения откроется окно Компиляция кода текстового редактора, и в этом окне и следует подготовить текст микропрограммы, состоящий из последовательности микрокоманд.

Формат микрокоманды (см. рис. 1.3) определяет структуру записи на языке микроассемблера. Определим элементы записи следующим образом:

< строка> ::= [<метка>][<микрокоманда>][#<комментарий>]

<микрокоманда> ::= [<последовательность микроопераций>]
[; <логическое условие>, <инверсия логического условия>, <метка>]

[<последовательность микроопераций>] ::= <микрооперация> [, <микрооперация>, <микрооперация> …] (не более пяти)

<микрооперация> 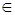{y_i}, i 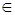{0, 1, 2, …, 32}

<логическое условие> 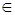{x_j, 0, 1}, j 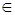{1, 2, 3, …, 6}

<инверсия логического условия> 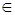{0, 1}

<метка> ::= <идентификатор>:

При разработке микропрограммы для последующей компиляции в среде модели ALU-1 арифметико-логического устройства необходимо соблюдать следующие правила:

■ в одной строке должно находиться не более одной микрокоманды (возможно, помеченной);

■ идентификаторы меток перехода, микроопераций и логических условий должны существовать;

■ идентификаторы меток не должны дублироваться.

Для разделения полей в микропрограмме используются следующие знаки:

■ «,» (запятая) – для разделения микроопераций в последовательности микроопераций;

■ «;» (точка с запятой) – для отделения поля переадресации от поля микроопераций;

■ «:» (двоеточие) – для отделения идентификатора метки от следующей за ней микрокоманды;

■ «#» (хэш) – для отделения комментария от микрокоманды, причем комментарий распространяется от символа «хэш» до конца строки;

■ «+n» – директива сдвига команды на n адресов (n задается десятичным целым числом).

Примерами микрокоманд могут являться следующие строки:

y26, y2 # передача слова из регистра C в регистр A

y4, y6, y8, y16, y25 # алгебраическое сложение слов
# из регистров A и B и передача полученной суммы
# в регистр D без сдвига

y28; 1, 0, L2 # сброс триггера DL и безусловный переход
# на метку L2 (в качестве логического условия
# используется константа 1)

y28; x1, 0, L2 # сброс триггера DL и переход на метку
L2 при условии x1 = 1

y4, y32, y18; x2, 1, L3 # сдвиг слова из регистра A
влево и переход на метку L3 при x2 = 0 (поскольку
флаг инверсии логического условия равен 1)

L3: y21 # микрокоманда завершения микропрограммы,
помеченная идентификатором L3

Если микрокоманда содержит только последовательность микроопераций, то компилятор по умолчанию добавляет поля переадресации ; 000, 0, 0000000, что соответствует тождественно ложному условию без инверсии, т. е. выполняется переход по адресу, который на единицу больше текущего.

При работе операционного автомата под управлением автомата с программируемой логикой необходимо предварительно загрузить в память модели управляющего автомата код микропрограммы. Проиллюстрируем эти действия на примере алгоритма сложения двоичных слов в прямом коде. В табл. ?? каждая строка определяет действие, выполняемое операционным автоматом или выбор адреса следующей микрокоманды. Формат микрокоманды управляющего автомата (см. рис. 1.3) содержит как поля микроопераций, так и поля переадресации. Поэтому в каждой микрокоманде можно задать действие операционного автомата и выбрать адрес следующей микрокоманды. Таким образом, две последовательные строки табл. ??, первая из которых определяет микрооперации, а вторая – переход, реализуются с помощью одной микрокоманды управляющего автомата. Если же после одной операционной микрокоманды следует другая, то на нее (на вторую) осуществляется безусловный переход.

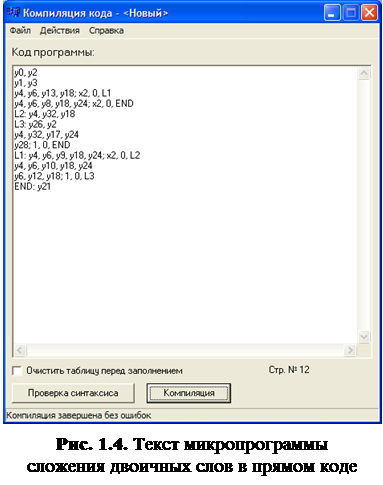
Учитывая эти правила и приведенный выше синтаксис, можно записать текст микропрограммы для сложения двоичных слов в прямом коде на микроассемблере (рис. 1.4).

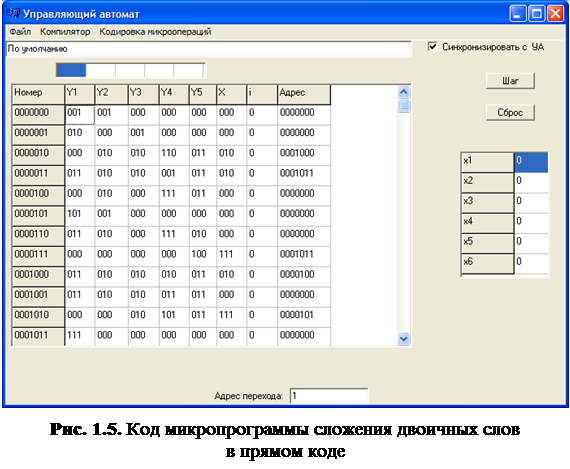
После успешной компиляции микропрограмма будет готова к исполнению, а память микропрограмм управляющего автомата будет иметь вид, представленный на рис. 1.5.

После этого можно перейти в окно операционного автомата, выполнить из его меню команду Настройки ► Управление ► Управляющий автомат и выполнять микропрограмму сложения с различными операндами в пошаговом или в автоматическом режиме.

Дата добавления: 2014-11-08; просмотров: 589; Нарушение авторских прав

Мы поможем в написании ваших работ!