Проверка теоремы Штейнера

Теорема Штейнера утверждает, что момент инерции тела J'₁ относительно произвольной оси О₁О₂ (рис.2) равен сумме момента инерции J₁ относительно оси, параллельной данной и проходящей через центр масс тела точку О (ос О'₁О'₂) и произведения массы тела m на квадрат расстояния между осями а²:

J'₁ = J₁ + ma². (10)

Для экспериментальной проверки теоремы Штейнера используют два одинаковых тела (сплошных цилиндра), массы которых равны m.

1. Поместить эти тела одно на другое строго по центру платформы и привести систему в крутильные колебательные движения.

2. Определить период колебаний, используя методику упражнения 1.

3. Рассчитать момент инерции двух цилиндрических тел J₂ (с учетом платформы) по формуле (8).

4. Рассчитать момент инерции двух тел J₁, расположенных на оси вращения платформы как разность J₁ = J₂ – J₀.

5. Расположить эти два тела на платформе симметрично на некотором расстоянии от оси вращения, определить период колебаний.

6. Рассчитать момент инерции двух тел, находящихся на некотором расстоянии от оси вращения (с учетом J₀ платформы) J'₂ по формуле (8). Особое внимание обратить на правильное определение расстояния от тел до оси вращения, используя рис.2.

О₂ О'₂

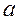
O₁ О'₁

Рис. 2.

7. Рассчитать момент инерции двух тел, находящихся на некотором расстоянии от оси вращения J'₁, как разность J'₁ = J'₂ – J₀.

Разница в числовых значениях J'₁ и J₁, составляет смысл теоремы Штейнера, а именно:

J'₁ – J₁ = 2ma², (11)

где m – масса одного тела; а – расстояние от оси вращения до центра цилиндра. Измерить а штангенциркулем или линейкой, проводя измерения несколько раз.

8. Оценить погрешность этого опыта.

Упражнение 4.

1. Определить момент инерции твердого тела неправильной геометрической формы, выполняя пункты упражнения 2.

2. Сделать письменный вывод по работе.

Контрольные вопросы.

1. Что такое момент инерции? Чему он равен у произвольного тела и у тел правильной геометрической формы: диска, цилиндра, шара?

2. Вывести формулу момента инерции ненагруженной платформы.

3. От каких факторов зависит точность этих опытов? Почему необходимо пользоваться малыми углами поворота платформы при крутильных колебаниях?

4. Сформулировать теорему Штейнера и объяснить, как она проверяется в данной лабораторной работе.

5. Можно ли пользоваться предложенным методом для определения моментов инерции тел в том случае, если ось вращения платформы не проходит через их центр тяжести?

Литература.

1. Киттель Ч., Найт У., Рудерман М. Берклеевский курс физики. Т. 1. М.: Наука, 1975.

2. Матвеев А.Н. Механика и теория относительности. М.: Высшая школа, 1976.

3. Руководство к лабораторным занятиям по физике (Под ред. Л.Л. Гольдина). М.: Наука, 1964.

4. Сивухин Д.В. Общий курс физики. Т. 1. М.: Наука, 1977.

Лабораторная работа № 7

Дата добавления: 2014-11-08; просмотров: 829; Нарушение авторских прав

Мы поможем в написании ваших работ!