Определение моментов инерции твердых тел с помощью трифилярного подвеса

Цель работы: определение моментов инерции твердых тел и проверка теоремы Штерна методом крутильных колебаний.

Приборы и принадлежности: трифилярный подвес, секундомер, рулетка, набор тел, подлежащих измерению.

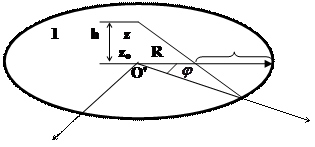
Одним из методов определения моментов инерции твердых тел, является метод крутильных колебаний, осуществляемый с помощью трифилярного подвеса (рис.1), который состоит из платформы 1, подвешенной на трех симметрично закрепленных нитях к неподвижно закрепленному диску 2 меньшего диаметра. Центры масс диска 2 и платформы 1 находятся на одной оси ОО', относительно которой платформе можно сообщить крутильные колебания, при этом центр тяжести платформы точки О' перемещается по этой оси.

Пусть верхняя платформа связана с системой координат ОХУ, начало которой находится в центре этой платформы в точке О. При повороте нижней платформы на некоторый угол j относительно положения равновесия, возникнет момент сил, стремящийся вернуть платформу в положение равновесия. В результате этого платформа начнет совершать крутильные колебания. Она поднимается на высоту h = z₀ – z, где z₀ – координата точки О' в положении равновесия; z – координата точки О', соответствующая углу поворота j .

Рассчитать момент инерции самой платформы, а также платформы с телом, помещенным на нее, можно из следующих соображений.

При вращении платформы ее центр тяжести поднимается на высоту h = z₀ - z, приобретая потенциальную энергию П = mgh, где m – масса платформы; g – ускорение свободного падения.

По закону сохранения механической энергии, пренебрегая работой сил трения, эта потенциальная энергия равна наибольшему значению кинетической энергии вращательного движения в момент достижения платформой положения равновесия.

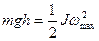, (1)

где J – момент инерции платформы; w – угловая скорость платформы в момент прохождения положения равновесия. Считая, что платформа совершает гармонические колебания, запишем зависимость углового смещения платформы от времени:

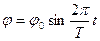, (2)

где j _о – амплитудное угловое смещение платформы, Т – период колебаний.

z

B

A

C

y x

R–r

Рис.1. Схема трифилярного подвеса.

Угловую скорость w найдем как первую производную от углового смещения (2).

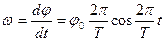. (3)

Наибольшего значения модуль угловой скорости достигает при прохождении платформой положения равновесия, т.е. в моменты времени, когда cos 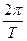t = 1. Т.е. t = 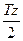, где z – целые числа. С учетом этого из (3) получим

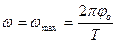. (4)

Подставляя (4) в (1), имеем

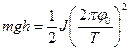. (5)

Высоту поднятия центра тяжести можно рассчитать из следующих соображений (рис.1). Точка С имеет координаты: x₁= r, y₁ = 0, z₁ = 0, а точка С' имеет координаты: x₂ = R cosj, y₂ = R sinj, z₂ = z. Расстояние между точками С и С' равно длине нити l.

Учитывая, что расстояние между двумя точками, координаты которых х₁, у_1, z₁и х₂, у₂, z₂ выражается формулой

,

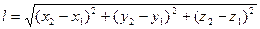получим

,

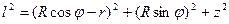откуда

.

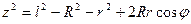В случае малых углов соsj = 1 – 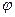²/2 имеем

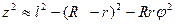. (6)

Так как l² = z_о² + (R + r)² ( рис.1), формула (6) принимаем вид

z² = z_о² – R rj² .

Разлагая 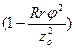в ряд и ограничиваясь первыми двумя членами ряда (ввиду малости j), получим

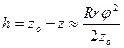. (7)

С учетом (7) из соотношения (5) получаем расчетную формулу:

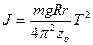. (8)

Эта формула дает возможность определить момент инерции нижней платформы (или платформы с телом), если известны параметры трифилярного подвеса: масса платформы m, радиусы большой и малой платформ R и r, расстояние между платформами z_о. Период колебаний определяется по формуле

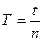, (9)

где t – время всех колебаний; n – число полных колебаний платформы.

Упражнение 1.

Определение момента инерции ненагруженной платформы J₀ по формуле (8).

1. С помощью штангенциркуля и линейки измерить величины R, r, z_о (масса платформы указана на самой платформе).

2. Осторожно вынести платформу из положения равновесия, повернув ее на небольшой угол j_о (3-5⁰) , и отпустить ее, предоставив ей возможность совершать крутильные движения. При этом следить, чтобы платформа не совершала побочных колебаний.

3. С помощью секундомера определить время 20-30 колебаний платформы и определить период колебаний по формуле (9).

4. Рассчитать момент инерции платформы J₀ по формуле (8).

5. Оценить погрешность определения J₀, проведя опыты 3 раза.

Упражнение 2.

Определение момента инерции тела, имеющего форму цилиндра.

1. Поместить исследуемое тело (цилиндр) по центру нижней платформы. Приводя в колебание платформу с телом, определить период колебаний по формуле (9), используя методику упражнения 1.

2. Рассчитать момент инерции платформы с телом J по формуле (8), где m – масса платформы и тела. Массу тела определить, взвешивая его на весах с разновесами.

3. Рассчитать момент инерции тела J_т как разность: J_т = J – J₀.

4. Сравнить полученные результаты с расчетом момента инерции сплошного цилиндра по формуле J = 1/2mr².

5. Объяснить полученные расхождения в результатах.

Упражнение 3.

Дата добавления: 2014-11-08; просмотров: 477; Нарушение авторских прав

Мы поможем в написании ваших работ!